基于离散元的鱼饲料仿真参数标定与试验
郭三琴,万鹏,2,杨俊,邓志勇,汪帅帅,朱明,2,谭鹤群,2
1.华中农业大学工学院,武汉 430070;2.农业农村部长江中下游农业装备重点实验室,武汉 430070
投饵机的结构是影响投饲均匀性的重要因素。在对投饵机结构进行优化时通常需要研究饲料颗粒与饲料颗粒间、饲料颗粒与投饵机接触部件间的相互作用。由于饲料颗粒与饲料颗粒间、饲料颗粒与投饵机接触部件间的相互作用情况复杂,基于传统理论分析和经验公式设计的投饵机与实际生产出来的投饵机其投饲效果之间通常存在较大差异[1-2]。随着数值模拟软件在农业工程领域的不断应用,利用离散元法(discrete element method,DEM)对农业装备关键部件的结构进行辅助设计可以显著提高设计效果[3-4]。基于离散元法对投饵机投饲过程进行仿真模拟时,为确保仿真结果准确度,需选取正确的离散元模型,设定精确的物性参数[5-6]。物性参数包括本征参数和接触参数,本征参数是指物体本身的特征参数,与实际数值一致,可通过台架试验测定。由于颗粒模型与真实颗粒形状不完全一致,导致仿真接触参数与真实值存在较大差异,且有些参数直接测定难度较大[7],因此需要结合台架试验与仿真试验对接触参数进行标定。
目前,国内外学者基于离散元法已对多种农业散粒体物料进行了参数标定。Coetzee等[8]结合剪切和压缩试验标定了玉米离散元模型的摩擦因数和刚度。焦俊等[9]利用单轴压缩试验标定了莲藕主藕体的本征参数。张锐等[10]利用试验堆积角和模拟堆积角对比的方法标定了沙土间接触参数。彭飞等[11]通过注入截面法直接获取大猪饲料颗粒的堆积轮廓图,并对其进行休止角测定,从而标定了大猪饲料间的接触参数。此外,部分学者利用台架试验与仿真试验相结合的休止角试验对水稻[12]、小麦[13]、微型马铃薯[14]、麻山药[15]、三七种子[16]等农产品进行了物性参数标定。综上所述,国内外研究人应用离散元仿真参数标定的对象主要为农产品、土壤、粉末状饲料等,但对渔用颗粒饲料的物性参数未有较为全面的研究,相关参考参数缺乏。因此,对渔用硬颗粒饲料的物性参数进行全面标定具有重要意义。
本研究以淡水养殖渔用硬颗粒3.0 中号饲料为研究对象,通过台架试验测定硬颗粒饲料的本征参数,在EDEM 中建立硬颗粒饲料的离散元模型,结合台架试验与仿真试验,标定硬颗粒饲料-钢、硬颗粒饲料-尼龙之间的接触参数,结合堆积角试验,通过最陡爬坡试验、Box-Behnken 响应面优化试验,确定硬颗粒饲料间的最优接触参数组合,通过自主设计的投饵机进行参数验证试验,以期得到全面的硬颗粒饲料物性参数,进一步为投饵机结构设计与优化提供参考。
1 材料与方法
1.1 物料本征参数测定
物料的本征参数主要包括密度、剪切模量、弹性模量、泊松比等[17]。本研究以通威126 型渔用3.0 中号柱形硬颗粒饲料为试验对象,开展水产饲料的本征参数测定研究。通过测定,试验所用硬颗粒饲料样本的含水率为9%~10%,直径为3.1~3.3 mm,长度为6.6~8.6 mm。
1)密度测定。随机选取完整硬颗粒3.0 中号饲料100颗,利用电子分析天平(日本岛津AUY220型,精度0.1 mg)测量每颗饲料质量mi,利用数显游标卡尺(精度0.01 mm)测量对应饲料颗粒的直径di和长度li,计算每颗饲料的体积vi,进而计算得出每颗饲料的密度ρi。计算所选100 颗硬颗粒饲料样本的密度及平均值,可得硬颗粒饲料的平均密度为ρ=(1 096±27)kg/m3。
2)弹性模量、剪切模量与泊松比的测定。随机选取完整硬颗粒3.0 中号饲料20 颗,利用质构仪(TMS-Pro 型,美国FTC 公司)开展单轴平板压缩试验(图1)。设置平板压缩速度为1 mm/min,起始力为0.2 N,在确保饲料不发生破碎断裂的情况下最大压缩距离设定为1 mm,测量每颗饲料压缩前后的直径与长度,计算得到饲料压缩前后的直径及长度变化量。

图1 单轴平板压缩试验Fig.1 Uniaxial plate compression test
对选取的20 颗硬颗粒饲料样本进行试验,参考文献[18]中物理公式计算每颗硬颗粒饲料的弹性模量、剪切模量、泊松比的值并计算各参数的平均值,可得硬颗粒饲料的弹性模量、剪切模量、泊松比分别 为(336.32±9.80) MPa、(126.65±4.13) MPa、0.33±0.02。
1.2 物料与接触面间接触参数测定
1)饲料颗粒仿真模型。渔用硬颗粒饲料外观呈较为规则的柱形,随机选取完整的硬颗粒3.0 中号饲料100 颗,量取每颗饲料直径di与长度li,计算平均值,可得硬颗粒饲料平均直径d为3.25 mm,平均长度l为7 mm。根据饲料的实际形状及参数,采用球颗粒组合的方式[19],建立硬颗粒饲料模型,如图2所示。

图2 硬颗粒饲料离散元几何模型Fig.2 DEM model of hard pellet feed
硬颗粒饲料球颗粒直径取3.25 mm,球颗粒接触模型选择Hertz-Mindlin 无滑移模型。结合上文对硬颗粒饲料本征参数的测定结果,并参照文献[20-21]中接触材料钢材、尼龙的本征参数,确定硬颗粒饲料与接触材料的本征参数,如表1所示。
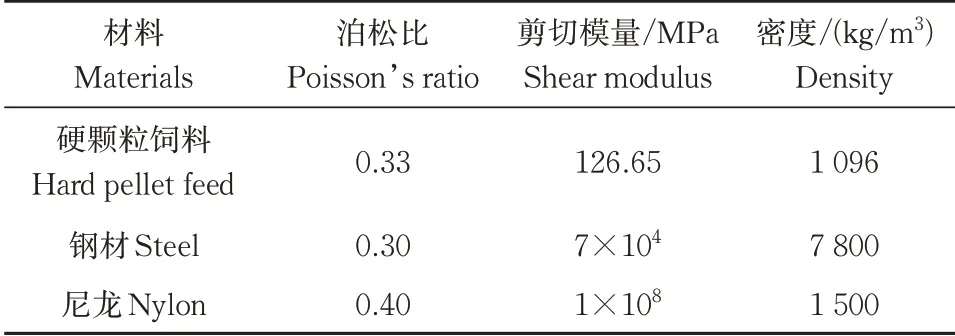
表1 饲料与材料的本征参数Table 1 Intrinsic parameter of feed and materials
2)碰撞恢复系数。利用碰撞弹跳试验测定硬颗粒饲料-钢、硬颗粒饲料-尼龙之间的碰撞恢复系数。试验操作过程如图3A所示。以硬颗粒饲料-钢为例,将钢板水平放置于试验台上,将渔用硬颗粒3.0 中号饲料从高度H1=200 mm 处释放,饲料自由落体接触到钢板时反向弹起,使用高速摄像机采集记录饲料反弹时的最高位置h1;同时,为保证台架试验与仿真试验的一致性,颗粒下落时,保持柱形颗粒的下底面接触钢板,进行10 次台架重复试验,计算平均值,可得硬颗粒饲料-钢、硬颗粒饲料-尼龙实际最高反弹高度分别为ha=(31.70±3.65)mm、hb=(35.60±2.88)mm。
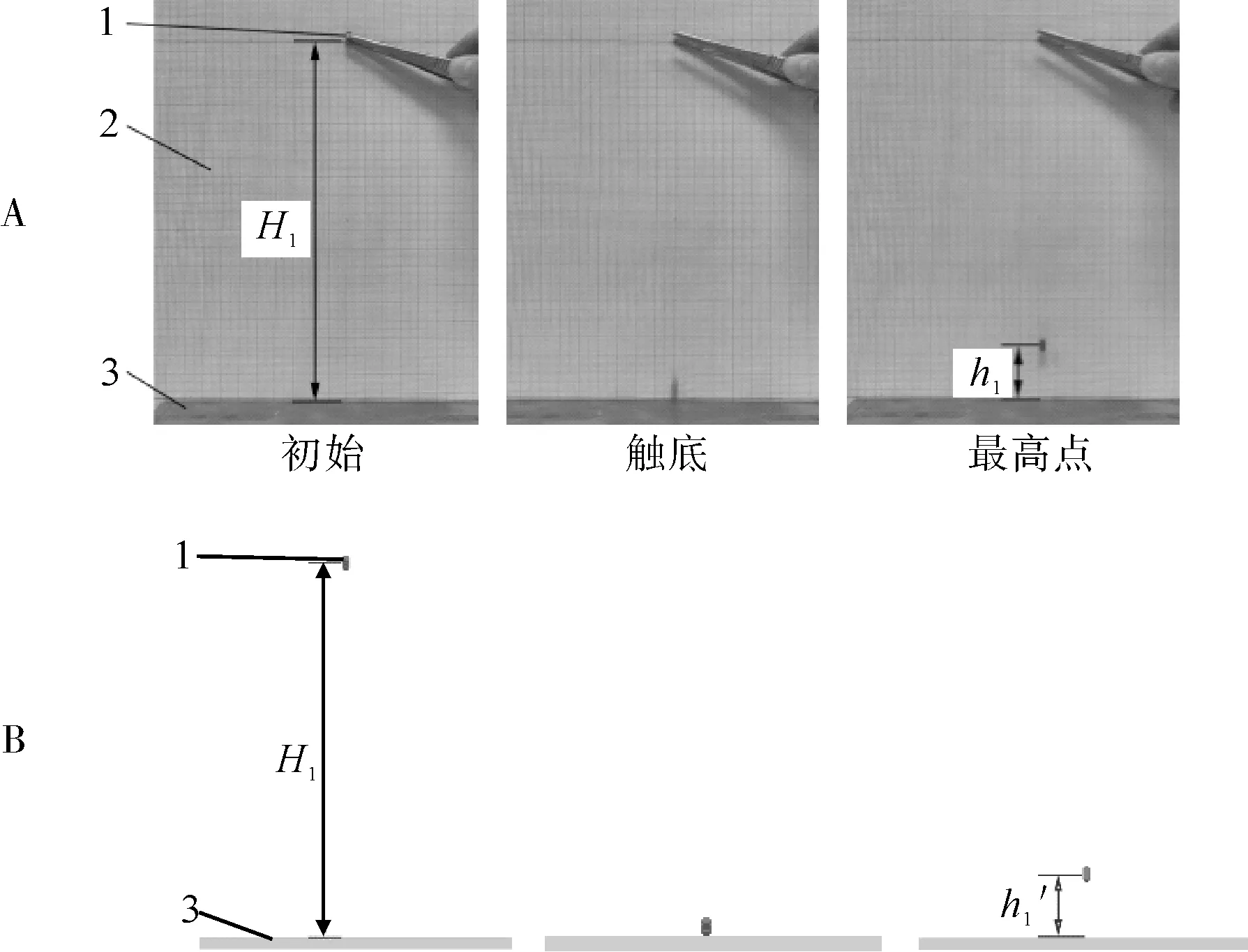
图3 碰撞恢复系数标定试验Fig.3 Calibration experiment of restitution coefficient
EDEM 仿真试验如图3B 所示,选取已建立的硬颗粒饲料模型,输入已标定硬颗粒饲料和钢的本征参数,设置饲料颗粒进行初速度为0 的自由落体运动,由于硬颗粒饲料与钢之间的静摩擦因数、滚动摩擦因数,硬颗粒饲料间的碰撞恢复系数、静摩擦因数、滚动摩擦因数对反弹高度没有影响,为避免干扰将这5个参数均设置为0。
为了确定硬颗粒饲料在不同材料表面的碰撞恢复系数,以实际最高反弹高度值ha、hb为目标值,在EDEM 中设置不同的参数进行大量预仿真试验,确定硬颗粒饲料-钢、硬颗粒饲料-尼龙之间的碰撞恢复系数x1a、x1b均在0.35~0.45 范围内,取步长为0.05,每个组合进行6 组仿真试验,y1a表示对应硬颗粒饲料-钢之间的碰撞恢复系数x1a的仿真最高反弹高度值,y1b表示对应硬颗粒饲料-尼龙之间的碰撞恢复系数x1b的仿真最高反弹高度值,试验设计方案与结果如表2所示。
对表2中的数据进行曲线拟合,构建硬颗粒饲料和接触材料间的碰撞恢复系数与仿真最高反弹高度值之间的拟合方程如下:
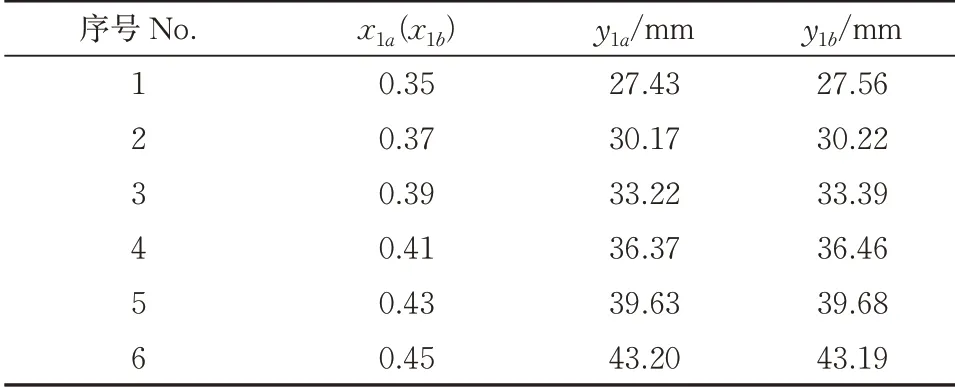
表2 碰撞恢复系数仿真试验方案Table 2 Simulation test scheme and results of restitution coefficient
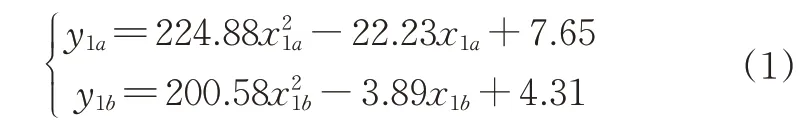
式(1)中,2 个二次拟合方程的决定系数R2值依次为0.999 9、0.999 8,均接近1,表明这2 个拟合方程均具有较高的可靠性。将通过台架试验测得实际最高反弹高度ha(31.70 mm)、hb(35.60 mm)分别带入式(1)中2 个二次拟合方程,得出饲料与接触材料之间的碰撞恢复系数x1a、x1b分别为0.38、0.405;将所得结果带入EDEM 软件进行验证,每组试验重复5次,计算平均值,可得仿真最高反弹高度值分别为h'a=31.74 mm、h'b=35.75 mm,与目标值的相对误差分别为0.13%、0.42%,表明标定后的仿真结果与实测值基本一致,从而确定硬颗粒饲料-钢、硬颗粒饲料-尼龙之间的碰撞恢复系数分别为0.38、0.405。
3)静摩擦因数。利用斜面滑移试验测定硬颗粒饲料-钢、硬颗粒饲料-尼龙之间的静摩擦因数。试验操作过程如图4所示。

图4 静摩擦因数标定试验Fig.4 Calibration experiment of static friction coefficient
以硬颗粒饲料-钢为例,将渔用硬颗粒3.0 中号饲料放置于水平放置的钢板上,再将钢板一端绕另一端的底边缓慢匀速转动,直到硬颗粒饲料开始发生滑动,停止转动并记录钢板最大倾斜角度;为防止试验过程中硬颗粒饲料滚动,放置饲料时,保证柱形饲料中心轴与钢板旋转轴垂直。每个组合进行10次台架重复试验,计算平均值,可得硬颗粒饲料-钢、硬颗粒饲料-尼龙实际最大倾斜角分别为αa=(27.91±1.84)°、αb=(19.44±1.2)°。
EDEM 仿真试验时,选取已建立的硬颗粒饲料模型,输入已标定硬颗粒饲料与钢的本征参数以及硬颗粒饲料与钢之间的碰撞恢复系数,由于硬颗粒饲料与钢之间的滚动摩擦因数,硬颗粒饲料间的碰撞恢复系数、静摩擦因数、滚动摩擦因数对钢板最大倾斜角没有影响,为避免干扰,将这4 个参数均设置为0。
为了确定硬颗粒饲料在不同材料表面的静摩擦因数,设置饲料初速度为0,以实际最大倾斜角αa、αb作为目标值,在EDEM 中设置不同的参数进行大量预仿真试验,确定硬颗粒饲料-钢、硬颗粒饲料-尼龙之间的静摩擦因数x2a、x2b范围分别为0.40~0.65、0.25~0.50,取步长为0.05,每个组合进行6 组仿真试验;y2a表示对应硬颗粒饲料-钢之间的静摩擦因数x2a的仿真最大倾斜角,y2b表示对应硬颗粒饲料-尼龙之间的静摩擦因数x2b的仿真最大倾斜角,试验设计方案与结果如表3所示。
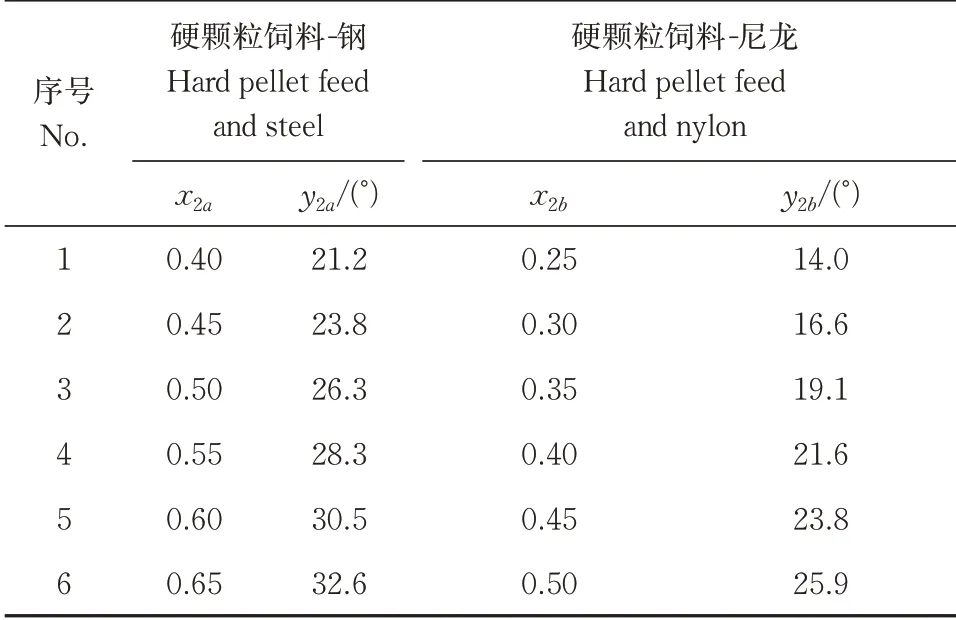
表3 静摩擦因数仿真试验方案Table 3 Simulation test scheme and results of static friction coefficient
对表3中的数据进行曲线拟合,构建硬颗粒饲料与接触材料间的静摩擦因数与仿真最大倾斜角之间的关系拟合方程如下:
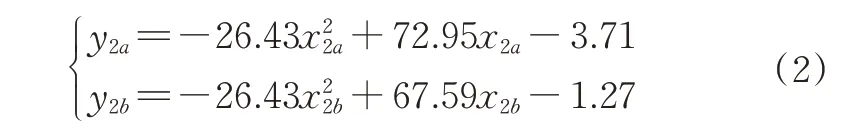
式(2)中,2 个二次拟合方程的决定系数R2值依次为0.999 5、0.999 9,均接近1,表明这2 个拟合方程均可靠有效。将通过台架试验测得实际最大倾斜角αa(27.91°)、αb(19.44°)依次带入式(2)中对应的2 个拟合方程,得出饲料与接触材料之间的静摩擦因数分别为x2a=0.538、x2b=0.356,将2 个静摩擦因数分别带入EDEM 软件进行验证,每组试验重复5 次,计算平均值,得出钢板与尼龙板最大倾斜角分别为α'a=28.2°、α'b=19.0°,与目标值的相对误差依次为1.04%、2.26%,表明标定后的仿真结果与实测值基本一致,从而确定硬颗粒饲料-钢、硬颗粒饲料-尼龙之间的静摩擦因数分别为0.538、0.356。
4)滚动摩擦因数。利用斜面滚动试验测定硬颗粒饲料-钢、硬颗粒饲料-尼龙之间的滚动摩擦因数,试验操作过程如图5所示。
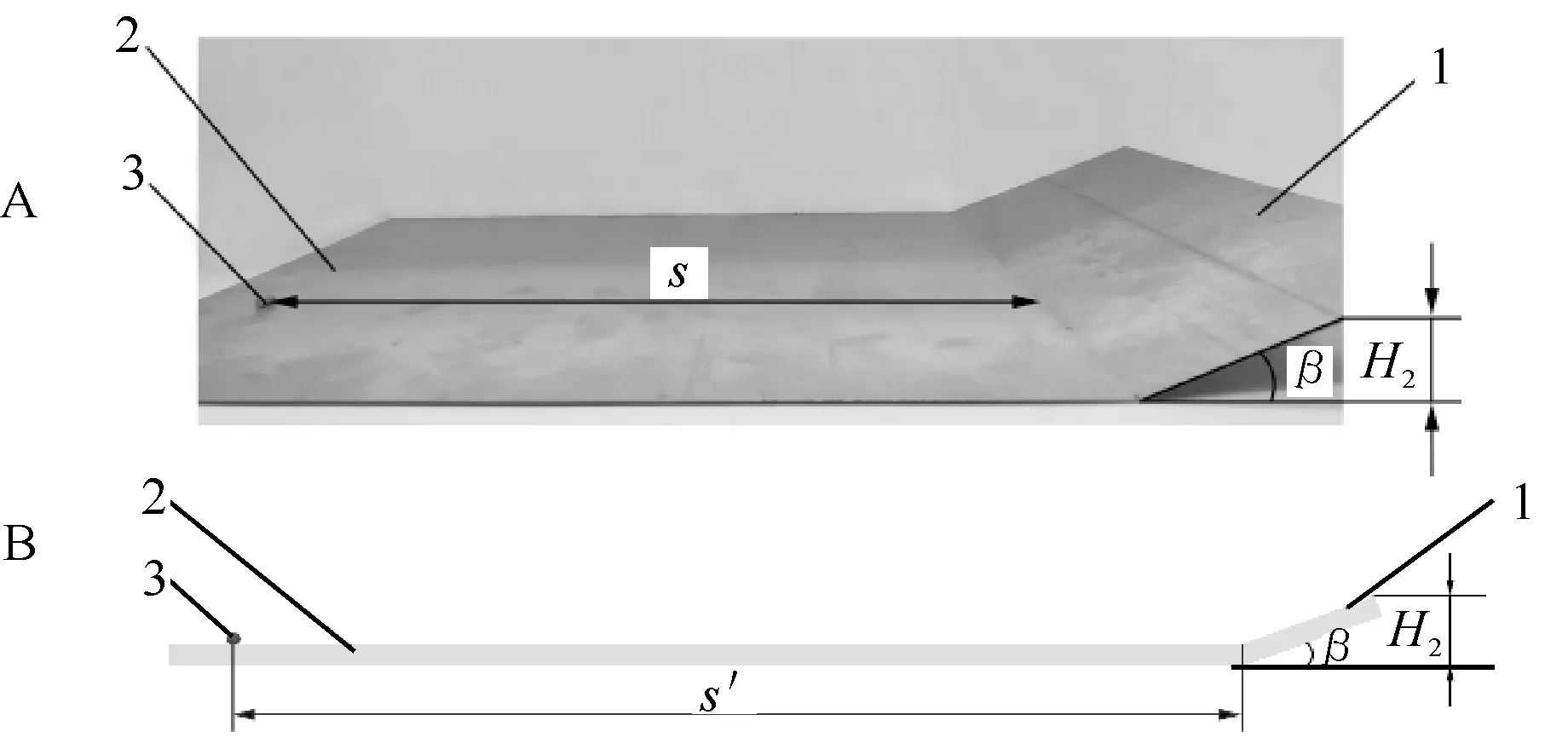
图5 滚动摩擦因数标定试验Fig.5 Calibration experiment of rolling friction coefficient
以硬颗粒饲料-钢为例,将折弯过的钢板水平放置在试验台上,倾斜钢板倾斜角β=20°,将渔用硬颗粒3.0中号饲料从高度H2=20 mm 处释放,饲料沿斜面做初速度为0 的滚动运动,在摩擦阻力的作用下,饲料滚动一段距离后停止。使用刻度尺测量饲料水平滚动的距离s,为保证实际试验环境与仿真试验的一致性,放置饲料时,保证柱形饲料中心轴与钢板折弯轴平行。进行10 次台架重复试验计算平均值,可得硬颗粒饲料-钢、硬颗粒饲料-尼龙的实际水平滚动距离分别为sa=(278.52±5.25)mm、sb=(234.97±6.08)mm。
EDEM 仿真试验时,选取已建立的硬颗粒饲料模型,输入已标定硬颗粒饲料与钢的本征参数、硬颗粒饲料与钢之间的碰撞恢复系数和静摩擦因数,由于硬颗粒饲料间的碰撞恢复系数、静摩擦因数、滚动摩擦因数对饲料在钢板上的水平滚动距离无影响,为避免干扰,将这3 个参数均设置为0。为了确定硬颗粒饲料在不同材料表面的滚动摩擦因数,设置饲料初速度为0,将实际水平滚动距离sa、sb作为目标值,在EDEM 中设置不同的参数进行大量预仿真试验,确定硬颗粒饲料-钢、硬颗粒饲料-尼龙之间的滚动摩擦因数x3a、x3b范围分别为0.026~0.036、0.03~0.055,取步长为0.05,每个组合进行6 组仿真试验;y3a表示对应硬颗粒饲料-钢之间的滚动摩擦因数x3a的仿真水平滚动距离、y3b表示对应硬颗粒饲料-尼龙之间的滚动摩擦因数x3b的仿真水平滚动距离,试验设计方案与结果如表4所示。
对表4中的数据进行曲线拟合,构建硬颗粒饲料与接触材料间的滚动摩擦因数与仿真水平滚动距离之间的关系拟合方程如下:
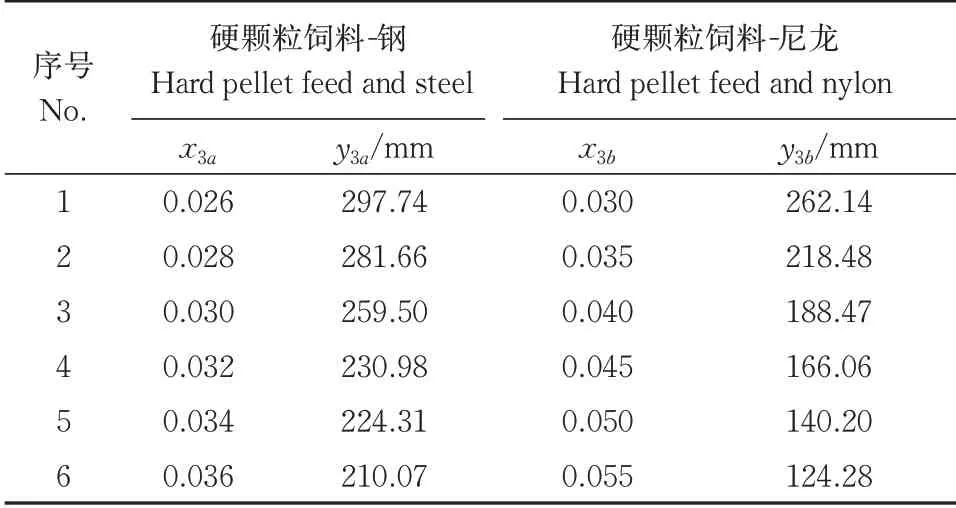
表4 滚动摩擦因数仿真试验方案Table 4 Simulation test scheme and results of rolling friction coefficient

式(3)中,2 个二次拟合方程的决定系数R2值依次为0.984 4、0.997 6,均接近1,表明这2 个拟合方程均可靠有效。将通过台架试验测得实际水平滚动距离sa(278.52 mm)、sb(234.97 mm)依次带入式(3)中2个二次拟合方程,得出饲料与接触材料之间的滚动摩擦因数分别为x3a=0.028、x3b=0.033,将2 个滚动摩擦因数分别带入EDEM 软件进行验证,每组试验重复5 次,计算平均值,可得仿真水平滚动距离分别为s'a=281.66 mm、s'b=237.13 mm,与目标值的相对误差分别为1.13%、0.92%,表明标定后的仿真结果与实测值基本一致,从而确定硬颗粒饲料-钢、硬颗粒饲料-尼龙之间的滚动摩擦因数分别为0.028、0.033。
2 结果与分析
2.1 饲料颗粒间接触参数标定
本研究采用圆筒提升法进行堆积角试验对硬颗粒饲料间的接触参数进行标定。由于前文已完成硬颗粒饲料与接触材料间的接触参数标定,进行硬颗粒饲料间接触参数标定时接触材料选择1 种即可。本研究选用内径60 mm、长度70 mm 的钢管作为接触材料进行堆积角试验,对硬颗粒饲料间的接触参数进行标定。
1)饲料堆积角试验。以渔用硬颗粒3.0 中号饲料为研究对象进行堆积角试验,具体试验过程如图6所示。将钢管竖直固定在万能材料试验机上,钢板水平放置。试验开始时,保持钢管下端面与钢板表面接触,在钢管内填充饲料颗粒与钢管上端面平齐;开启电源,设定万能材料试验机提升速度为300 mm/min,钢管随万能材料试验机匀速缓慢上升,饲料颗粒自由扩散在钢板上形成稳定堆积角。
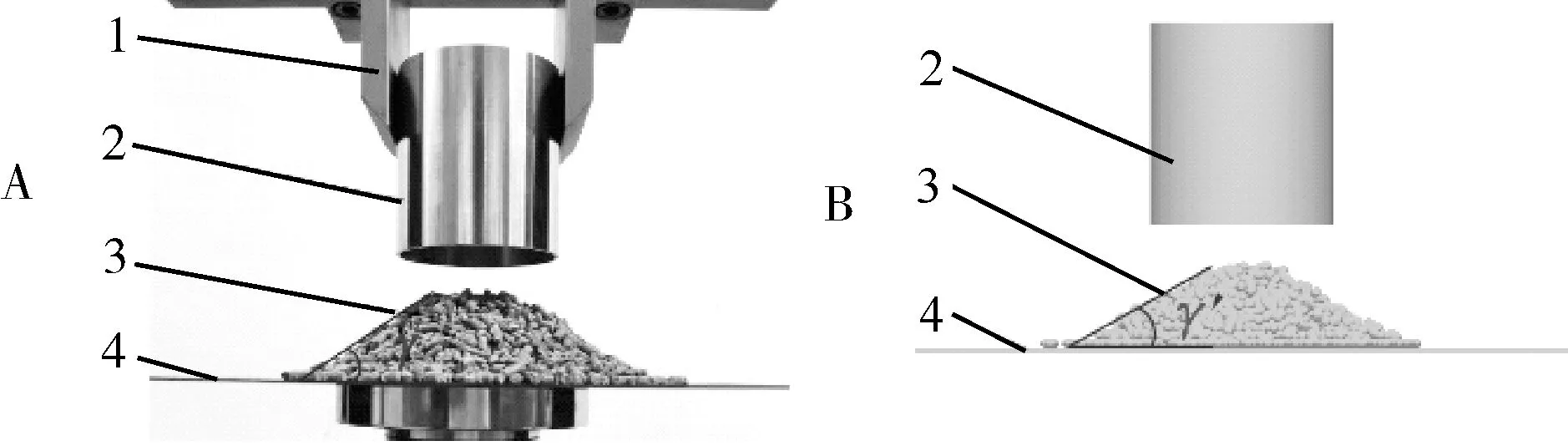
图6 堆积角试验Fig.6 Stacking angle test
采集饲料颗粒堆积图像,利用灰度化、二值化等图像处理算法提取堆积边缘线并进行线性拟合,则拟合直线与水平面间的夹角即为实际堆积角,如图7所示。
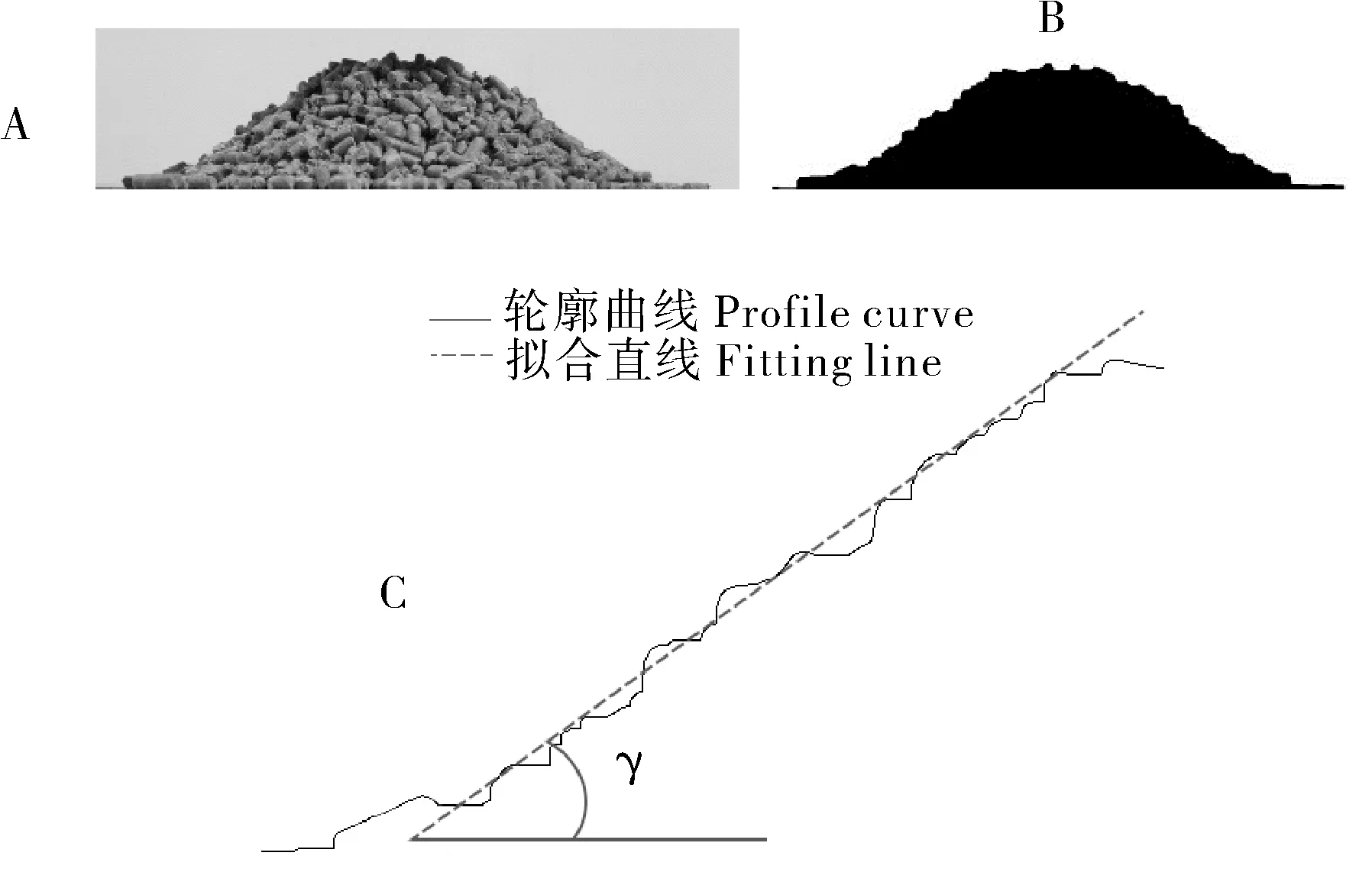
图7 堆积角图像处理Fig.7 Image processing of stacking angle
称量可得钢板上硬颗粒饲料的质量为136.5 g,进行10 次重复试验,统计每次试验的饲料堆积角并计算其平均值,可得硬颗粒饲料实际堆积角γ=(31.1±1.70)°。
采用EDEM 软件进行仿真试验(图6B),选取建立的硬颗粒饲料模型,输入已标定的硬颗粒饲料与钢的本征参数以及硬颗粒饲料与钢之间的接触参数,设置饲料颗粒质量为136.5 g,生成时间1.5 s,待颗粒生成且稳定后,钢管以300 mm/min 匀速上升,钢管中饲料颗粒缓慢扩散堆积,形成稳定堆积角。获取仿真试验得到的饲料颗粒堆积图像进行灰度化、二值化等处理,提取堆积边缘线进行直线拟合,拟合直线与水平面间的夹角即为仿真堆积角γ'。
为了确定硬颗粒饲料间的碰撞恢复系数、静摩擦因数、滚动摩擦因数的取值,以台架试验测得实际堆积角γ作为目标堆积角,以仿真堆积角与目标堆积角的相对误差δ作为评价指标,设置不同的参数进行大量预仿真试验,确定硬颗粒饲料间的碰撞恢复系数、静摩擦因数、滚动摩擦因数范围分别为0.20~0.50、0.10~0.40、0.05~0.20,在此范围内进行最陡爬坡试验。
2)最陡爬坡试验。以台架试验获得的硬颗粒饲料实际堆积角γ作为目标堆积角,硬颗粒饲料间碰撞恢复系数X1、静摩擦因数X2、滚动摩擦因数X3为试验因素,仿真堆积角γ'与目标堆积角γ的相对误差δ作为评价指标进行最陡爬坡试验,通过寻找最为接近目标值的仿真堆积角,确定硬颗粒饲料间3个接触参数的最优组合。仿真堆积角与目标堆积角相对误差δ计算式为:

式(4)中,γ'为仿真堆积角,(°);γ为目标堆积角,(°)。
最陡爬坡试验设计方案与结果如表5 所示。由表5 可看出,随着试验因素值增大,硬颗粒饲料仿真堆积角与目标堆积角相对误差δ呈现出先减小后增大趋势,且在4 号试验得到最小相对误差值。因此,将4号组作为0水平,3号和5号分别作为低水平和高水平进行BBD(Box-Behnken design)响应面试验设计。
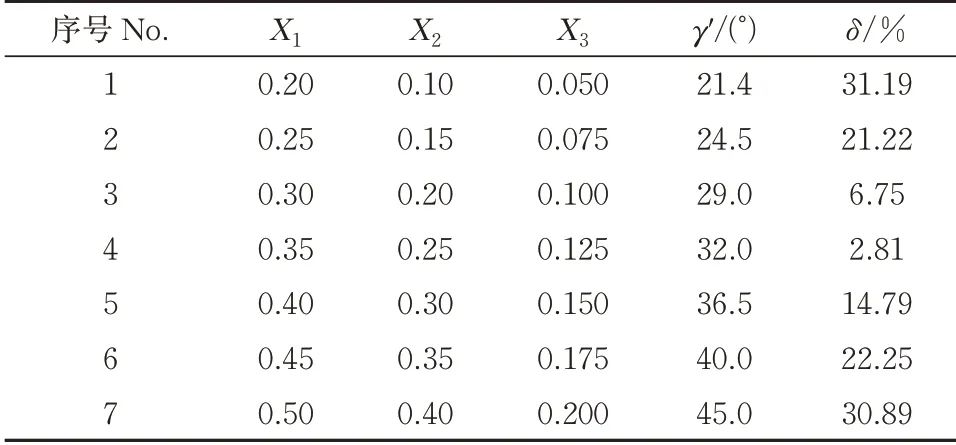
表5 最陡爬坡试验方案Table 5 The scheme and results of steepest climbing test
3)方差分析与回归模型建立。基于Design-Ex⁃pert 11 进行BBD 响应面试验设计,以硬颗粒饲料仿真堆积角γ'与目标堆积角γ的相对误差δ作为试验指标,X1、X2、X3分别表示硬颗粒饲料间碰撞恢复系数、静摩擦因数、滚动摩擦因数,试验因素编码如表6所示。试验中心设置5 组重复,试验结果如表7所示。
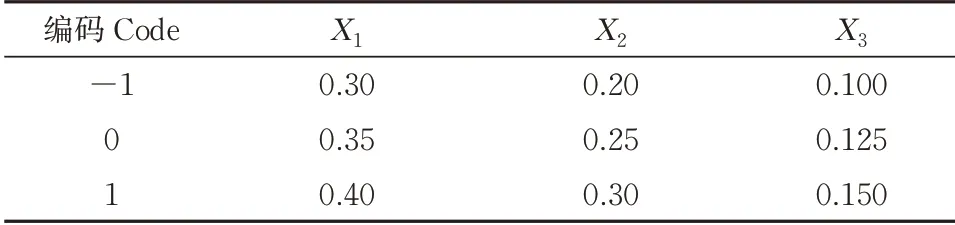
表6 试验因素编码Table 6 Coding of factors

表7 响应面试验设计与结果Table 7 Design and results of Box-Behnken test
应用Design-Expert 11 软件对试验结果进行多元回归拟合分析,可得硬颗粒饲料仿真堆积角与目标堆积角相对误差δ的回归方程,对回归方程进行显著性检验,结果如表8 所示。由表8 可知,二次回归模型(P<0.000 1)极显著,失拟项(P=0.824 9>0.05)不显著,回归方程不失拟,拟合效果好,具有预测意义。X1、X1X2、X2X3、X12、X22、X32对δ影响极显著,X1X3影响显著,X2、X3影响不显著,各因素对试验指标δ的影响由大到小分别为:碰撞恢复系数、静摩擦因数、滚动摩擦因数。经逐步回归法剔除影响不显著项,得各因素与试验指标δ回归方程为:

由表8 可知,虽然X2、X3对试验指标δ无显著影响,但2 个因素的平方项X22、X32及因素间交互项X1X2、X2X3对δ影响极显著,交互项X1X3对δ影响显著,因此不可忽视这2个因素对试验指标的影响。
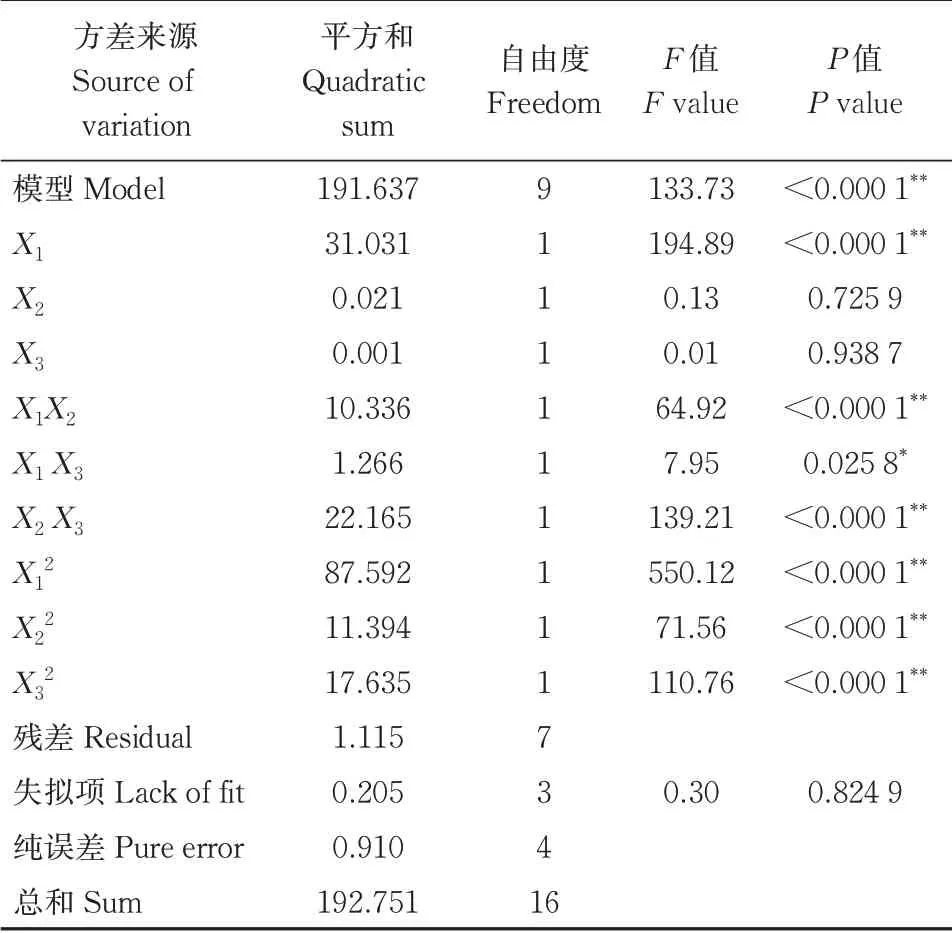
表8 回归方程方差分析Table 8 Variance analysis of regression equation
4)响应面分析和参数优化。采用Design-Expert 11 软件进行响应面分析,以直观分析因素间交互作用对试验指标的影响情况。设定硬颗粒饲料间碰撞恢复系数X1为0.35、静摩擦因数X2为0.25、滚动摩擦因数X3为0.125,因素间交互作用对硬颗粒饲料堆积角相对误差δ的影响如图8所示。
由图8 可知,随着碰撞恢复系数X1、静摩擦因数X2、滚动摩擦因数X3的增加,硬颗粒饲料堆积角相对误差δ均呈现出先减小后增大的趋势,且3 个因素对δ的影响显著性由大到小依次为X1、X2、X3,与方差分析所得结果一致。
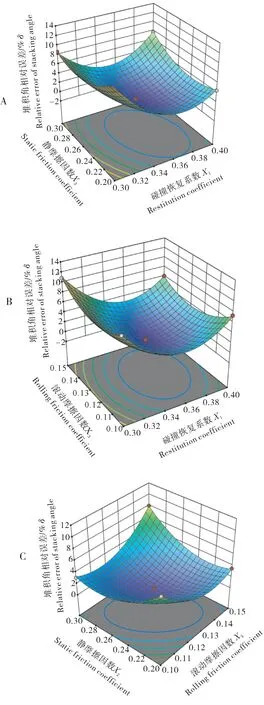
图8 试验因素对硬颗粒饲料堆积角相对误差的影响Fig.8 Effects of experimental factors on relative error of hard pellet feed stacking angle
应用Design-Expert 11 软件的参数优化模块,以表6 中各因素范围为约束条件,以试验指标δ回归方程式(5)为目标函数,求解其最小值,得出硬颗粒饲料间接触参数最优参数组合为碰撞恢复系数0.364,静摩擦因数0.236,滚动摩擦因数0.13,此时,堆积角相对误差为1.721%。将所得的最优参数组合进行仿真堆积角试验验证,得硬颗粒饲料仿真堆积角γ'=31.6°,与硬颗粒饲料实际堆积角γ(31.1°)之间的相对误差为1.608%,与优化结果基本吻合,表明所得饲料间最佳参数组合可用于EDEM仿真试验。
2.2 优化参数验证
为了验证渔用硬颗粒饲料离散元模型以及仿真参数的准确性,采用自主研发设计的投饵机样机进行硬颗粒饲料抛撒试验。该投饵机主要由料箱、下料装置、抛撒装置组成,工作原理为料箱中的饲料靠自身重力作用落入下料装置中下料辊的凹槽内,下料装置旋转下料,凹槽内饲料随之旋转至下料装置出料口时,饲料自由落入抛撒装置中匀速转动的离心转盘上,饲料在离心力的作用下沿离心转盘边缘的切线方向抛出,抛出的饲料经圆台挡板改变其运动方向,最终落到收集区域内,设置转盘转速为300 r/min。其中,下料辊、离心转盘为尼龙材料,其他部件均为钢材。硬颗粒饲料抛撒试验如图9所示。

图9 硬颗粒饲料抛撒试验Fig.9 Centrifugal dispersion test of the hard pellet feed
验证试验以硬颗粒饲料分布变异系数CV为评价指标,饲料收集区域为直径4 m 的圆面,其网格划分方式如图10所示。

图10 区域划分网格布置图Fig.10 Area division grid layout
将圆面沿径向划分为面积相等的5个圆环面,沿周向划分为8个面积相等的圆锥面,即将整个饲料收集区域划分为40 个面积相等的网格区域,每个网格区域的面积为0.314 m2。试验时,使收集区圆面圆心位于离心转盘中心线上,圆面距离离心转盘底部的距离为1.0 m。由于饲料颗粒下落接触地面时会产生弹跳、滑动、滚动等运动,影响试验结果的准确性,且与饲料颗粒落入水面时的实际状态不符。因此,本研究选用加绒地毯对下落的饲料颗粒进行收集。
抛撒试验完成后,统计硬颗粒饲料落在每个网格区域内的质量mi,并计算饲料分布变异系数CV。
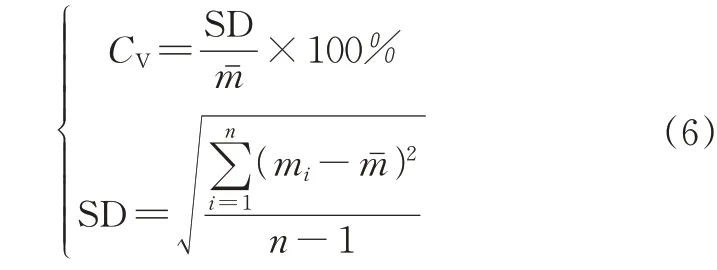
式(6)中,CV为饲料分布变异系数,%;SD 为标准差,g;n为网格区域数量,n=40;mˉ为n个网格区域内收集的饲料质量平均值,g;mi为第i个网格区域收集的饲料质量,g。
选用通威126型渔用硬颗粒3.0中号饲料1 000 g进行饲料抛撒试验,将饲料颗粒装入料箱,开启电源进行抛撒试验,待饲料颗粒全部抛撒完后关闭电源,统计落在每个网格区域内的硬颗粒饲料质量mi,并计算分布变异系数CV,试验重复5 次计算平均值,得实际硬颗粒饲料分布变异系数CV=1.092%。
根据台架试验参数进行仿真饲料抛撒试验,如图9B 所示。将投饵机模型以及硬颗粒饲料模型导入EDEM 离散元软件,同时输入已标定的硬颗粒饲料物性参数;在投饵机下方放置直径为4 m 的落料圆板,设置硬颗粒饲料与落料圆板间的碰撞恢复系数为0、静摩擦因数为1、滚动摩擦因数为1,确保饲料落在落料圆板上时不发生运动。设置落料圆板圆心位于离心转盘中心线上,圆板上表面位于离心转盘底部的距离为1 m。在落料圆板上方建立饲料质量检测区域,绘制如图10所示的饲料质量检测区域模型,并将其导入EDEM 软件后处理模块Setup Selec⁃tions。设置饲料质量检测区域模型的位置参数,使饲料质量检测区域模型下表面与落料圆板上表面完全重合。最后设置饲料质量检测区域中饲料颗粒的检测方式为各个网格区域内的饲料累计质量。仿真试验结束后,统计饲料检测区域中经过各网格区域内的硬颗粒饲料模型的质量mi',并计算其分布变异系数CV',试验重复5次计算平均值,得仿真硬颗粒饲料分布变异系数CV'=1.073%。
根据台架试验和仿真试验结果可知,硬颗粒饲料在进行台架试验和仿真试验时的分布变异系数相对误差为1.74%,且饲料颗粒在收集区域中的分布情况基本相同,这表明硬颗粒饲料的离散元模型以及标定后的硬颗粒饲料的物性参数可用于离散元仿真试验。
3 讨 论
本研究通过试验测定了硬颗粒饲料的本征参数。根据密度公式求出硬颗粒饲料的密度为1.096 kg/m3,通过单轴平板压缩试验结合物理公式得出硬颗粒饲料的弹性模量、剪切模量、泊松比分别为336.32 MPa、126.65 MPa、0.33。建立了硬颗粒饲料的离散元模型,结合台架试验与仿真试验标定了硬颗粒饲料与接触材料间的接触参数,即硬颗粒饲料-钢板、硬颗粒饲料-尼龙板的碰撞恢复系数、静摩擦因数、滚动摩擦因数分别为0.380、0.538、0.028,0.405、0.356、0.033。采用圆筒提升法进行堆积角试验,基于Design-Expert 11 软件对试验数据进行方差分析、响应面分析和参数优化,得出硬颗粒饲料间最优接触参数组合,并对最优参数组合进行仿真堆积角试验验证,从而确定硬颗粒饲料间的碰撞恢复系数为0.364、静摩擦因数为0.236、滚动摩擦因数为0.13。利用自主研发的投饵机进行硬颗粒饲料抛撒试验,以硬颗粒饲料分布变异系数CV为评价指标,设置相同的试验参数进行台架试验与仿真试验,试验结果显示,实际硬颗粒饲料分布变异系数为1.092%,仿真硬颗粒饲料分布变异系数为1.073%,即台架试验与仿真试验的硬颗粒饲料分布变异系数相对误差为1.709%,表明本研究所建立的渔用硬颗粒饲料离散元模型以及所标定的硬颗粒饲料物性参数可用于离散元仿真试验。

