广义余弦二维主成分分析

王肖锋 陆程昊 郦金祥 刘军

伴随人工智能与模式识别的迅猛发展,从海量 高维数据中提取能够有效表征事物或现象本质属性的特征是一件十分有意义的工作.主成分分析(Principal component analysis,PCA)[1]是一种常见的特征提取与数据降维方法,其目标是利用一组新的正交基向量去描述原始高维数据,且满足在投影后的子空间中数据方差最大,从而使得由投影方向构成的低维特征空间能够较好体现原高维数据的空间结构信息.随后,针对二维图像矩阵的特征提取,相继提出了二维主成分分析(Two-dimensional PCA,2DPCA)[2]、双向二维主成分分析(Two-directional 2DPCA,(2D)2PCA)[3]、行列顺序二维主成分分析(Sequential row-column 2DPCA,RC-2DPCA)[4]和对角线主成分分析(Diagonal PCA,Diagonal-PCA)[5].RC2DPCA 和(2D)2PCA 分别在行列两个方向上实现了数据降维,而Diagonal-PCA 在对角线上进一步保留了数据行列间的相关性.近年来,相关PCA 研究已在人脸识别[6]、语音识别[7]、字符识别[8]及姿势识别[9]等众多领域得到广泛应用.

上述提及的PCA 方法均采用欧氏距离的平方作为目标函数的距离度量方式,对噪声、离群数据或其他扰动较为敏感,重构误差很大,使得实际投影方向偏离了真实的投影方向,进而影响到算法的鲁棒性.针对鲁棒特征提取研究,主要有两个思路:1)将高维数据P∈Rh×w分解成低秩结构矩阵A和含噪稀疏矩阵E,考虑到优化模型的凸松弛问题,得到优化模型 m in‖A‖*+λ‖E‖1s.t.P=A+E,其各种求解算法均需进行奇异值分解,计算复杂度高.在处理海量高维数据时,其求解算法容易受到复杂度的制约[10-12];2)沿用PCA 投影方差最大的思路,在其目标函数中采用其他范数代替欧氏距离的平方进行距离度量,使得算法具有鲁棒性.

L1范数被认为是基于投影距离进行鲁棒降维的最有效手段[13-14].Kwak[15]提出了基于L1 范数的PCA-L1方法,试图在投影子空间中寻求基于L1范数的最大投影距离,并采用了贪婪迭代求解算法,相较于欧氏距离平方的度量方式,该方法具有较强的鲁棒性.Nie等[16]提出了基于PCA-L1的非贪婪迭代求解算法,且满足基于L1范数的目标函数最优.针对L1范数在不同数据结构相关信息进行正则化时所遇到的稳定性问题,Lu等[17]提出了基于L1范数的自适应正则化的PCA-L1/AR 方法,同时考虑了鲁棒性及数据的相关性.Wang[18]和Li等[19]针对块主成分分析(Block PCA,BPCA)分别提出了基于L1范数的BPCA-L1方法的贪婪求解和非贪婪求解算法.为了更有效表征数据空间结构,如同将PCA 扩展到2DPCA[2]一样,Li等[20]和Wang等[21]则将PCA-L1延伸到2DPCA-L1,分别提出了2DPCAL1的贪婪求解和非贪婪求解算法.Wang等[22]结合2DPCA-L1的鲁棒性和稀疏诱导回归模型,提出了具有稀疏约束的2DPCA-L1-S 方法.Pang等[23]和Zhao等[24]则进一步将PCA-L1推广到基于L1范数的鲁棒张量子空间学习.考虑到L1范数和L2范数均为Lp范数的特例,相继提出了PCA-Lp[25]、LpSPCA[26]和G2DPCA-Lp[27].所有的上述鲁棒降维方法均寻求在不同范数下样本投影距离最大的目标优化问题,但其原始图像与重构图像之间的重构误差并未优化,且失去了PCA 和2DPCA 原欧氏距离平方中L2范数的旋转方差属性.

为了更有效获得旋转方差属性,Li等[28]则用F范数替代2DPCA的平方 F 范数,作为距离度量方式构建目标函数.与现有2DPCA-L1相比,基于F范数的2DPCA 不仅对离群数据具有较强的鲁棒性,还能很好揭示其旋转不变性的几何结构.Wang等[29]提出了 F 范数最小化的最优均值2DPCA(OMF-2DPCA),空间属性维度的距离采用 F 范数度量,而不同数据点求和则采用L1范数度量.上述方法利用F范数度量重构误差[29]或者子空间下投影距离[28],其重构误差最小并不等效于投影距离最大,因此,需考虑同时将重构误差与数据投影距离两者集成到目标函数中.为此,Gao等[30]提出了Angle-2DPCA方法,采用 F 范数作为目标函数的距离度量方式,通过最小化重构误差与投影距离的比率获得最优的投影矩阵,实现了在投影距离最大的基础上使其重构误差尽可能小.但Angle-2DPCA 直接针对数据矩阵进行降维,忽略了矩阵行列之间的异常信息,其鲁棒性受到了一定程度的限制.

本文借鉴前人研究成果,提出一种基于广义余弦模型的二维主成分分析,并给出其迭代贪婪的求解算法.本文结构如下:第1 节对相关目标函数的优化问题进行分析,给出了广义余弦模型的目标函数;第2 节提出GC2DPCA的求解算法并进行理论分析;第3 节在人工数据集及Yale、ORL 及FERET人脸数据集上进行实验并加以分析;第4 节进行总结.

1 问题提出

1.1 相关目标函数的优化问题

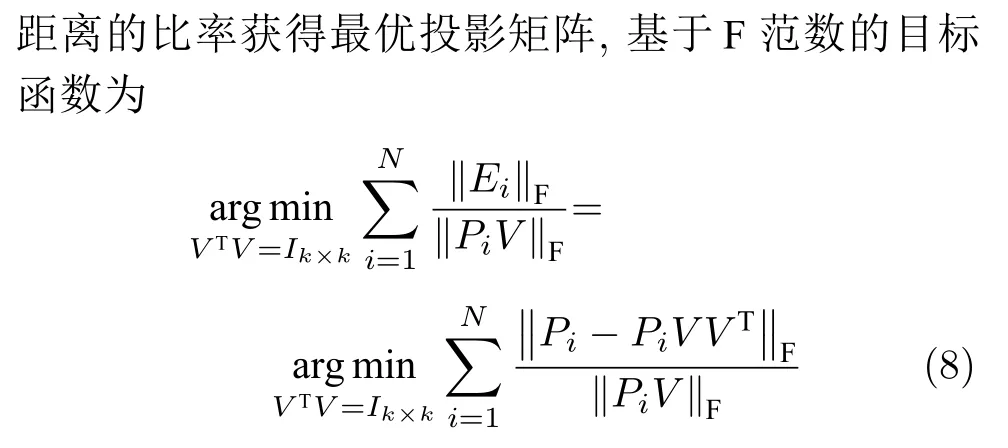
相较于2DPCA,Angle-2DPCA 不仅减弱了远距离离群点的影响,而且在优化投影距离最大的基础上兼顾了重构误差的影响.

从前述分析可知,范数的距离度量方式和目标函数均影响到各个算法的鲁棒性.从距离度量方式考虑,L2范数的相关算法寻求数据投影方差最大的优化目标,容易放大离群点的作用,导致求得的PC失真,鲁棒性较差.L1范数对数据投影的绝对值进行优化,相比于L2范数的投影方差,降低了对离群点的敏感性. F 范数因存在不等式相关算法[28-29]将重构误差作为目标函数的优化问题,但并未考虑投影距离最大化,反之也亦然.从目标函数的两个方面考虑,基于 F 范数的Angle-2DPCA 算法[30]将重构误差与投影距离的比率作为目标函数,有利于解决两个目标的优化问题.但从数据投影角度考虑,进一步分析目标函数(8),优化重构误差与投影距离的比率实质上是一个正切模型.其目标函数中的分子与分母均置于 F 范数度量下,且均受到同一投影矩阵V的制约.因此,Angle-2DPCA的重构误差与投影距离很难实现同时优化.

1.2 广义余弦模型

传统L2范数的平方会放大离群数据的主导作用,其鲁棒性较差;L1范数虽能降低离群数据的敏感性,但无法有效控制数据投影后的重构误差.此外,Angle-2DPCA 直接针对数据矩阵进行鲁棒降维,不利于抑制数据矩阵行列之间的异常值,算法的鲁棒性受到一定限制.鉴于这些问题,受Angle-2DPCA[30]的目标函数启发,本文构造一个基于广义余弦模型的目标函数,在满足数据投影距离最大的基础上使得其重构误差较小.

假设零均值化后矩阵样本集为P,则基于余弦模型的目标函数定义为

其中,v∈Rw×1表示V中前k个PC 中任意一个,θij表示第i个样本的第j行Pij与v的夹角,|Pijv|为数据的投影距离,也可写为‖Pijv‖2.

为了调整行向量Pij的距离度量方式,将式(9)推广延伸得到广义余弦模型为

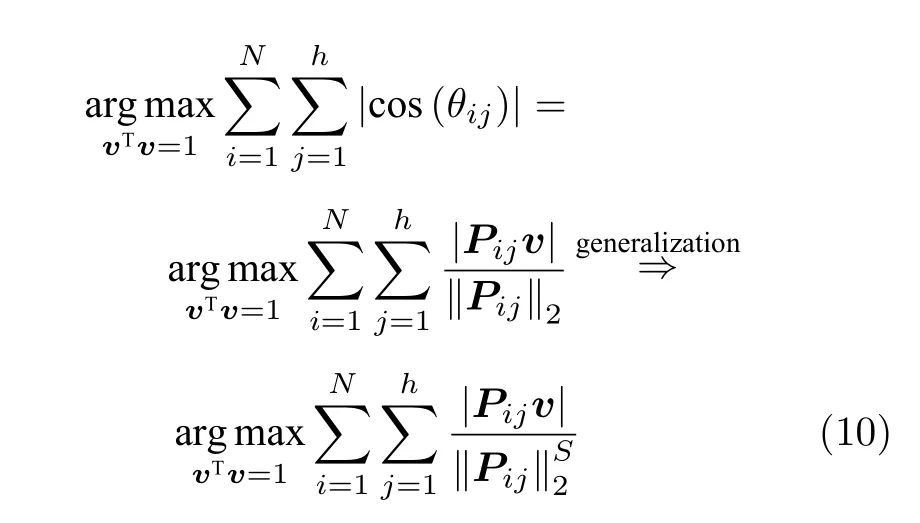
化简式(10),可得

广义余弦模型与Angle-2DPCA的目标函数形式一样,均为比值形式.Angle-2DPCA的重构误差与投影距离中均呈现同一投影矩阵V.在 F 范数的距离度量方式下,其重构误差与投影距离相互受到牵制.因此,Angle-2DPCA 最终无法真正实现投影距离最大与重构误差较小的双目标优化.而广义余弦模型仅在投影距离中呈现投影向量v,其重构误差最小与投影距离最大的目标优化能力得以加强.其次,从带权重lij的数据优化问题考虑,若Pij是离群数据,则会较大,权重系数lij会相当小.因此,其提取的PC也就更逼近真实PC,离群数据得到抑制.此外,从受离群数据干扰的百分比R考虑,RGC2DPCA≤RAngle-2DPCA,广义余弦模型采用行向量的优化方式可以减少受污染样本干扰的百分比,其鲁棒性也能得以进一步增强.

图1 广义余弦模型Fig.1 Generalized cosine model

2 GC2DPCA 算法

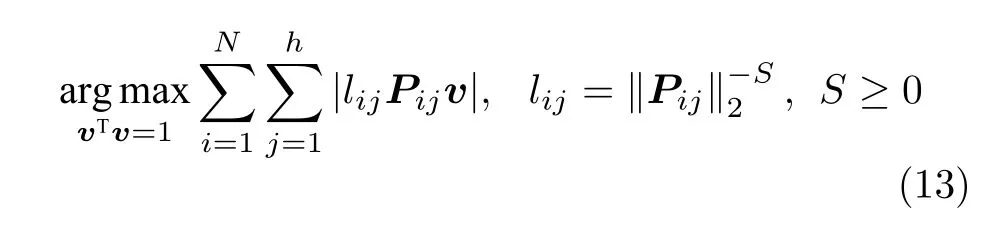
对于该问题求解,采用迭代贪婪算法实现.

2.1 第一个主成分求解算法

针对投影矩阵V中的第一个主成分v1的目标函数式表示为

其中,t为迭代步数.

将式(15)代入式(14),可得

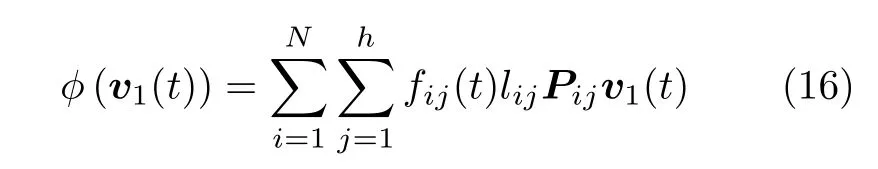
为了使得目标函数(13)最优,其迭代求解算法如下:

算法 1.GC2DPCA 第一个主成分求解算法

2.2 其余主成分求解算法

求解其余主成分依然利用贪婪求解算法,为了保证投影矩阵中的每个PC 与其他PC 是正交的,对其余PC 所对应的数据样本进行更新,则更新迭代式为

同理,为使目标函数(13)最优,其余主成分迭代求解算法如下:

算法 2.GC2DPCA的其余主成分求解算法

如同PCA-L1和2DPCA-L1的贪婪求解算法[15,20]一样,GC2DPCA 不能确保得到全局最优解.这种贪婪求解算法能够保证各个PC 之间在满足正交的同时,使得每一个PC 均依赖于提出的广义余弦模型.在求解各个PC 时离群数据能够得到抑制,其重构误差也能间接得到控制.此外,贪婪算法使得各个PC 之间满足如式(18)的迭代关系.当提取PC 数增加时,之前计算的PC 得以保留.通过迭代,可进一步计算更高阶PC.

3 实验结果与分析

为验证本文算法的有效性及鲁棒性,采用人工数据集、Yale、ORL 及FERET 人脸数据集分别进行实验,并对PCA、PCA-L1[15]、2DPCA[2]、2DPCAL1[20]、2DPCA-L1(non-greedy)[21]、Angle-2DPCA[30]以及本文所提的GC2DPCA 算法进行实验对比分析.鲁棒性实验主要用于判定各算法目标函数中的重构误差损失情形,而相关性实验用于判定各算法在满足投影距离最大时求得PC的真实程度,分类率实验则将求得的PC 用于判定分类识别效果,时间复杂度实验用于判定各个求解PC 算法的复杂程度.实验软件环境为Windows7、Microsoft Visual Studio 2010 和OpenCV 2.4.10,采用Intel i5-5200U (2.2 GHz)处理器,8 GB 内存的硬件环境.

3.1 鲁棒性实验与分析

考虑上述数据集已进行零均值化,以平均重构误差(Average reconstruction error,ARCE)为性能指标,进行鲁棒性实验与对比分析.

当数据矩阵需先向量化时:

当数据矩阵无需向量化时:

其中,NI表示未受到噪声干扰的样本数量.

3.1.1 人工数据集

分别构建如图2(a)和图2(c)所示的二维人工数据集(已被零均值),数据集表示为ξi={(xi,yi),i=1,2,···,24}.其中,五角星代表离群数据点,圆圈代表纯净数据点,Real 表示排除离群数据点后利用L2范数度量方式提取的第一个PC的方向,Angle为Angle-2DPCA[30]中的比率度量方式.受离群数据点的影响,通过各个算法提取的第一个PC 方向与Real的接近程度来判断其鲁棒性.

图2 人工数据集的平均重构误差Fig.2 ARCE on the artificial datasets

从图2(a)可以看出,基于L2范数的度量方式提取的第一个PC 方向受离群数据点影响最大,而L1范数更靠近Real 方向,因此,与L2范数相比,L1范数对噪声相对不敏感.Angle 度量方式更接近Real 方向,具有较强的鲁棒性.随着广义余弦模型参数S的变化,其鲁棒性顺序依次为CosineS=1.5 ＞ CosineS=2 ＞ CosineS=1 ＞ Angle ＞CosineS=2.5 ＞ CosineS=0.5 ＞L1-norm ＞L2-norm.利用上述度量方式提取的第一个PC 再重构原始数据,借助式(19)计算得到其相应的ARCE 分别如图2(b)和图2(d)所示.从图2(b)可以看出,L2范数度量方式下其重构数据能力最差,其ARCE 最大.L1范数和Angle的ARCE 均有不同程度下降,当CosineS=1.5 时,其ARCE 最小.因此,随着参数S的变化,广义余弦模型重构数据能力优于其他距离度量方式,且随着参数S的逐步增加,其ARCE 先减少到最优值,然后再逐步增加,其ARCE 变化规律与图2(a)所示的鲁棒性分析一致.进一步分析参数S对鲁棒性的影响规律,从图2(c)和图2(d)可以看出,当CosineS=2 时,其ARCE最小,鲁棒性最优,并且变化规律与图2(a)和图2(b)分析完全一致.通过大量的重复实验可以得到,随着参数S的增加,广义余弦模型总存在一个相对最优值(对应ARCE 最小),其ARCE 规律是先逐步减少到某一个最优值,然后再逐步增大.在实际应用过程中,可根据上述变化规律寻求相对合理的参数S.

3.1.2 Yale、ORL 及FERET 人脸数据集

Yale 数据集包含15 个人脸图像,每人11 幅共165 幅,分辨率为 1 00×100 像素.ORL 数据集由40 个人脸图像组成,每人10 幅共400 幅,分辨率为 1 12×92 像素.FERET 数据集有20 人,每人7 幅共140 幅,分辨率为 8 0×80 像素.图3 展示了Yale、ORL 及FERET 三个数据集的部分图像.为了测试GC2DPCA算法的鲁棒性,采取文献[26]的方式对数据集进行加噪:1)遮盖噪声(Occluded noise).在40%遮盖噪声下,从Yale、ORL 及FERET 数据集中分别随机抽取总样本数的40%,在抽取的图像样本上对应加入 4 0×40 像素、4 0×40 像素和 3 0×30 像素的杂点噪声进行覆盖.在60%遮盖噪声下,从3 个数据集抽取60%图像样本上分别加入 6 0×60 像素、6 0×60 像素和 4 5×45 像素的杂点噪声进行覆盖.上述遮盖噪声位置随机且不超越图像边界,分别如图4 和图5 所示;2)哑噪声(Dummy noise).在整个数据集中额外增加总样本数的40%和60%杂点噪声样本,其分辨率与原数据集样本一致,如图6 所示.

图3 人脸数据集示例Fig.3 Examples of face datasets

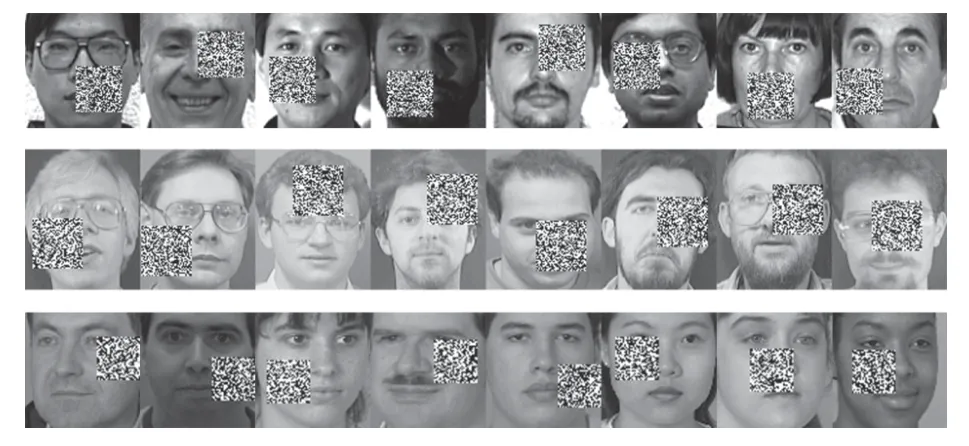
图4 40%遮盖噪声示例Fig.4 Examples with 40% occluded noise

图5 60%遮盖噪声示例Fig.5 Examples with 60% occluded noise

图6 哑噪声示例Fig.6 Examples with dummy noise

将具有40%和60%遮盖噪声的Yale、ORL 和FERET 人脸数据集投影到不同的主成分个数(Number of principal components,NPC)所组成的投影子空间上,利用式(19)及式(20)计算各个算法对应的ARCE 如图7 所示.从图7(a)～7(f)中可以得出如下结论:1)各个算法随着NPC的增加,其ARCE均呈现逐步下降趋势且逐渐趋于平缓,因此,其降维的子空间维数将对ARCE 影响很大.2)PCA 和PCA-L1因向量化而增加了数据维数,其ARCE 相比其他二维算法均偏大.随着NPC的增加,L1范数使得PCA-L1的最终鲁棒性要略优于PCA.3)对于2DPCA、2DPCA-L1、2DPCA-L1(nongreedy)及Angle-2DPCA 均为二维算法,直接针对图像矩阵进行特征提取,相比一维算法其ARCE 均大为减小.2DPCA 和2DPCA-L1(non-greedy)两个算法ARCE 差异不明显,且不受数据集及遮盖噪声影响.2DPCA-L1与2DPCA-L1(non-greedy)相比,其ARCE 具有明显优势,且不受数据集的影响.随着噪声的增加,2DPCA-L1其贪婪求解算法优势更趋明显.而Angle-2DPCA的ARCE 与2DPCA-L1较为接近.在遮盖噪声下,可知RGC2DPCA＜RAngle-2DPCA,因此,GC2DPCA 也优于Angle-2DPCA.4)相比上述其他算法,GC2DPCA的ARCE 具有较为明显的优势,且不受数据集的影响.当加入60%遮盖噪声后,GC2DPCA的ARCE在两个不同数据集下,与其他算法相比下降优势更趋明显,并且其ARCE几乎不变,而其他算法均有不同程度的增大.通过多次重复实验可得到,参数S改变对GC2DPCA的ARCE 略有变化,且参数S对ARCE 影响规律与人工数据集的变化规律一致,图7 各个子图为显示简洁仅呈现GC2DPCAS=1的情形.因此,针对遮盖噪声,本文所提算法GC2DPCA的鲁棒性均优于其他算法,并且加大噪声,其优势也愈加明显.

图7 不同遮盖噪声下的平均重构误差Fig.7 ARCE with different occluded noises

引入不同哑噪声之后,各个算法对应的ARCE如图8 所示.可以看出,GC2DPCA的鲁棒性可以得到与遮盖噪声实验的类似结论.1)当NPC 小于5 时,PCA的ARCE 下降较快,当NPC 大于10 时,PCA-L1比PCA的鲁棒效果十分明显,而PCA 几乎趋于常值.2)2DPCA-L1(non-greedy)在面对哑噪声时已经不如2DPCA,并且在图8(d)和图8(f)中其趋势不稳定,振动较大.3)其余算法ARCE 曲线走势与遮盖噪声实验中类似,进一步验证前述分析结论,不同的是GC2DPCA 与Angle-2DPCA 在不同数据集及不同哑噪声下几乎完全重叠.4)加大哑噪声后,各个算法的ARCE 变化很小.

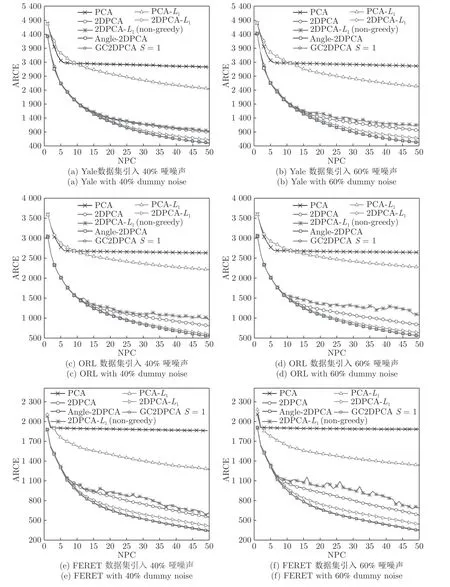
图8 不同哑噪声下的平均重构误差Fig.8 ARCE with different dummy noises

以上带遮盖噪声和哑噪声的人脸数据集上的鲁棒性实验结果表明,相比经典的PCA 和PCA-L1,本文所提算法优势十分明显;与2DPCA、2DPCAL1、2DPCA-L1(non-greedy)相比,降低了ARCE,提升了鲁棒性能;与Angle-2DPCA 相比,在大遮盖噪声下具有较为明显优势.而在哑噪声下,两者其样本污染情况一致,因均兼顾到数据的重构误差,则GC2DPCA 与Angle-2DPCA的ARCE 几乎完全相同.

3.2 相关性实验与分析

为验证各算法提取的PC 与真实PC 之间的相关性,用内积矩阵定义相关性,表示为

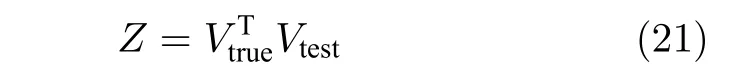
其中,Vtrue表示用L2范数计算纯净样本数据得到的PC 所构成的投影矩阵,Vtest为各个算法针对含噪数据计算得到的PC 构成的投影矩阵.显然,Z越接近单位矩阵,说明Vtest越接近Vtrue.选用Yale数据集的60%遮盖噪声进行相关性实验.各个算法实验结果如图9 所示,x轴和y轴分别代表Vtrue和Vtest中对应的NPC,z轴表示PC 之间内积的绝对值.因此,通过直观观察三维图中z值来判定算法的相关性.如对角线上的z值越接近1,而对角线以外区域越接近0,则表示内积矩阵Z相关性越高,求解的PC 也就越接近真实的PC.

图9 主成分相关性Fig.9 Correlations between principal components

从图9 可以看出,PCA 提取的主成分大部分偏离了真实值,对角线上仅有第一个PC 约为0.85,对角线上其余PC 均在0.5 以下.而PCA-L1也不太理想,对角线上的PC 与PCA 近似,对角线外其他区域与PCA 相比多了一些小凸峰,无法接近0,因此PCA-L1相关性不如PCA.2DPCA 对角线上前10 个主成分相关性几乎为1,对角线上其余PC锐减至0.6 以下,而对角线外其他区域凸峰严重,几乎逼近0.4.在2DPCA-L1中,与2DPCA 相比凸峰有向对角线方向收敛的趋势,其相关性得到一定程度的提升.而在GC2DPCA 中,随S参数逐渐增加,凸峰逐渐收敛到对角线上,当S=1.5 时最优,对角线上主成分相关性均在0.6 之上,而在对角线外其他区域几乎接近于0,因此,GC2DPCA 提取的主成分更接近真实值,且相互正交.可以看到,与前述算法不同的是,2DPCA-L1(non-greedy)和Angle-2DPCA 呈现一种杂乱的态势,这是由于这两个算法提取得到投影矩阵V中的各个主成分之间无顺序优先之分,它们对V中所有主成分是同时进行优化的.这两个算法在调整主成分数量时,需重新计算之前得到的所有主成分,这也是2DPCAL1(non-greedy)和Angle-2DPCA的不利之处.而图9 中其他算法均是在原始数据减去之前计算主成分分量之后再进行迭代计算,其相关性均优于2DPCAL1(non-greedy)和Angle-2DPCA.因此,本文提出的GC2DPCA 在相关性方面均远优于其他算法.

3.3 分类率实验与分析

分类率实验采用K-最近邻分类算法(K-nearest neighbor,KNN),并选取K=1 时进行分类.所有实验数据样本均经过零均值处理,其中训练样本和测试样本零均值化所采用的均值来源于训练样本的均值.在Yale 和ORL 数据集每个人脸图像中,随机抽取其中5 幅用作训练样本,其余用作测试样本.在FERET 数据集中,每人随机抽取3 幅用作训练样本,其余为测试样本.在3 个数据集中训练样本中随机抽取40%样本添加遮盖噪声.考虑到噪声的随机性,重复5 次随机遮盖噪声进行分类率实验,得到平均分类率分别如表1～3 所示.

从表1～3 可以看出,从求解算法看,2DPCAL1(non-greedy)和Angle-2DPCA 均为非贪婪算法,随着NPC的增加,其平均分类率逐渐增加,这是由于这两个算法求得的主成分随NPC 增加而逐步得到优化,与前述相关性分析结论一致.而对于其他贪婪算法,随着NPC的增加,各个算法平均分类率均有所下降.这是由于NPC 越多,包含的噪声成分也就越多,其分类率也就相应下降.从算法的维数看,一维算法(包括PCA 和PCA-L1)普遍低于其他二维算法,与文献[2]和[18]实验结果一致,这是由于二维算法提取了更多的图像模式特征,并且损失图像的行列结构信息偏少.从距离度量方式看,L1范数相关算法(PCA-L1和2DPCA-L1)大部分情形分类率要略高于L2范数相对应的算法(PCA 和2DPCA),这是由于L1范数度量方式具有一定的抗噪能力和分类优越性.基于 F 范数的Angle-2DPCA 算法与基于L1范数的算法2DPCAL1相比,分类率并无优势.而本文提出的GC2DPCA相比其他算法,具有较为明显的分类优势.随着参数S的增加,GC2DPCA 算法的分类率略有提升,但分类率并不明显.同样,在Yale、ORL 数据集以及FERET 中分别加入60%的遮盖噪声,得到平均分类率如表4～6 所示.可以看出,平均分类率总体趋势与添加少量噪声情形近似,但在大量噪声下所有算法的平均分类率均相应有所下降,这是由于在人为增加噪声时,使得投影距离减少所致.此外,GC2DPCA的平均分类率具有较为明显的优势.从表1～6 中的参数S对GC2DPCA 算法分类率的影响可以看出,随着参数S的增加,也存在一个近似最优的分类结果.如表2 所示,S=1.5 时呈现最优分类率.若增加噪声数据,如表5 所示,近似最优分类率的S值有前移迹象.从表1～6 中均可观察到此情况.因此,当噪声增加到可与原始数据相抗衡时,如增加S值可以更大程度地抑制噪声,但在某种程度上也抑制了真正有用的数据.因此,在大噪声的情况下可以选择略小的S值进行测试.另外,GC2DPCA 在提取少量PC的情况下分类率较高,NPC 越多引入噪声数量也越多,因此,在实际应用中可根据数据的维数选择较小的NPC 进行鲁棒降维.

表1 Yale 数据集下平均分类率 (40%遮盖噪声)(%)Table 1 Average classification rate under Yale dataset (40% occluded noise)(%)

表2 ORL 数据集下平均分类率 (40%遮盖噪声)(%)Table 2 Average classification rate under ORL dataset (40% occluded noise)(%)

表3 FERET 数据集下平均分类率 (40%遮盖噪声)(%)Table 3 Average classification rate under FERET dataset (40% occluded noise)(%)

表4 Yale 数据集下平均分类率 (60%遮盖噪声)(%)Table 4 Average classification rate under Yale dataset (60% occluded noise)(%)

表5 ORL 数据集平均分类率 (60%遮盖噪声)(%)Table 5 Average classification rate under ORL dataset (60% occluded noise)(%)

表6 FERET 数据集平均分类率 (60%遮盖噪声)(%)Table 6 Average classification rate under FERET dataset (60% occluded noise)(%)

3.4 时间复杂度实验与分析

参考上述所提及相关算法对应的文献,得到各个算法的时间复杂度如表7 所示.其中,t为迭代步数.PCA-L1、2DPCA-L1、2DPCA-L1(non-greedy)和GC2DPCA的迭代步数与样本数正相关,并且PCA-L1理论上比PCA 运算快,但2DPCA-L1因反而会比2DPCA运算速度慢.2DPCA-L1与GC2DPCA 复杂度一致.2DPCAL1(non-greedy)和Angle-2DPCA 求解过程包含奇异值分解,相应增加了算法的运算时间.Angle-2DPCA 算法收敛的原因在文献[30]中未加以解释,具体运算时间可在实验中间接得到.

表7 时间复杂度分析Table 7 Time complexity analysis

实验选用Yale 数据集的60%遮盖噪声进行实验,提取的NPC 设为10,分析各个算法提取PC所需时间随样本数的变化.此处,GC2DPCA 其参数S与时间复杂度无关,可设定S=1.

各个算法所需时间如表8 所示,可以看出,2DPCA相比于PCA 降低了数据维数,所需时间比PCA低.鲁棒算法PCA-L1的运行时间最快,因为其迭代样本数N较少.2DPCA-L1与GC2DPCA接近,但是余弦模型的引入抑制了离群噪声数据,使得PC方向往真实方向偏转较快,时间上略优于2DPCAL1. Angle-2DPCA 低于2DPCA-L1(non-greedy),但它们每次迭代均需奇异值分解,因此,Angle-2DPCA 与2DPCA-L1(non-greedy)所需时间均高于GC2DPCA.

表8 各个算法所需时间对比(s)Table 8 Comparison of the required time by each algorithm (s)

4 结束语

本文提出了一种基于广义余弦模型的GC2DPCA及其贪婪求解算法.广义余弦模型的引入使得样本中混入较多噪声数据时,算法依然能够呈现较好的鲁棒性,且其对于不同的遮盖噪声和哑噪声均具有一定的适应性.GC2DPCA 算法求解过程简单、易实现,理论层面证明了算法的收敛性及提取的主成分之间的正交性.其次,通过选择不同的S参数,可应用于更广泛的含离群数据的鲁棒降维,并在实验层面得到了S参数对算法的影响规律.将GC2DPCA与PCA 算法、PCA-L1算法、2DPCA 算法、2DPCAL1算法、2DPCA-L1(non-greedy)算法及Angle-2DPCA 算法在平均重构误差、相关性、分类率及时间复杂度等方面进行比较,本文算法在人工数据集、Yale、ORL 以及FERET 人脸数据集上的实验结果均具有更优的性能.然而,本文的算法并不能实现样本的增量迭代求解,将影响到算法的增量学习能力.因此,探索GC2DPCA 算法的增量求解形式值得进一步研究.