间歇过程的批内自优化控制

叶凌箭

化工过程普遍存在不确定性,如何采用有效的优化方法找到不确定条件下系统的真实最优点,对提高化工企业的经济效益发挥着关键作用[1].大规模化工过程的控制系统通常为分层递阶结构[2-3],控制层(下层)的主要任务是抑制底层扰动,跟踪优化层传递来的被控变量设定值,优化层(上层)根据调度层(顶层)传达的生产任务指标等,对当前工况进行识别,执行相应的优化算法计算出最优设定值,传递给控制层执行.

优化层执行的优化算法通常以化工过程的非线性模型为基础,以传统的“二步法” 实时优化[4-5]为例,首先确定模型的不确定参数,运行过程中采集系统的输出量数据,对未知参数进行估计,再基于更新的系统模型进行重优化,计算出被控变量的最优设定值后传递给控制层.这一过程通常还需要结合数据调和、稳态检测等技术手段加强优化结果的可靠性,工业过程的优化周期一般为4～8 小时.针对传统的“二步法”的缺点,近年来涌现出了新的实时优化方法,如Bonvin 课题组提出的修正项自适应方法(Modifier adaptation)[6-7],通过对标称模型的约束及梯度进行修正,即使不估计扰动参数也能收敛到真实最优点.文献[8-10]考虑运行层之间的不同时间尺度,提出了数据驱动的多速率分层运行优化控制方法,基于Q 学习对基础控制回路的设定值进行在线优化,使运行层能更好地优化控制性能指标.自优化控制(Self-optimizing control,SOC)[11-13]提出通过离线选择控制层的被控变量,设定值则在线保持不变,提供了实时优化的另一种研究思路.在自优化控制中,被控变量可以是常规物理量的函数,即构造虚拟量进行控制,可使系统的操作变量可以在不确定性下进行自寻优.当底层控制的优化作用较强时(经济损失可接受),甚至可以省略单独的优化层,从而简化控制系统.相比传统的优化方式,自优化控制的优化在工作频率为秒/分的反馈控制中完成,因此优化速度得到大幅度提升,在一系列研究中表现出良好的效果[14-17].

间歇过程是一类批次加工的化工过程,具有规模小、灵活性高的特点,在需求多元化的现代市场中应用越来越广泛.相比连续化工过程,间歇过程具有“多重时变”的操作特征[18-19].一方面,间歇过程具有重复特性,可以引入学习机制从历史批次的数据中提炼出有用的信息,改进后续批次的跟踪控制和经济指标优化,典型的如迭代学习控制[18,20-23]、批间实时优化[23-24]等控制和优化技术.另一方面,由于其时变特性,间歇过程在批次内无稳定操作点,相比连续过程的控制和稳态优化更具挑战[25-27].自优化控制经过近20 年的发展,针对连续过程已报道了一系列被控变量求解方法[12,28-31],但是针对需动态优化的间歇过程仍缺乏足够的研究.值得注意的是,由于从批间角度看间歇过程是一个静态过程[32],近年来文献[33-34]提出了间歇过程的批间自优化控制方法.此类方法仅利用了间歇过程的重复性,基于已有的静态自优化控制方法求解被控变量,然后设计批间控制器调节输入轨迹,逐批次将被控变量控制于恒定设定点,实现实时优化.但批间优化本质上还是静态方法,由于需要若干个批次才能实现被控变量的跟踪控制,优化作用慢,因此未充分发挥自优化控制的优势.此外,批间优化只对具有重复特性的扰动具有效果,当系统受到高频扰动作用时,批间控制器难以实现有效的实时优化.

最近,Ye等[35]提出了一种针对间歇过程的动态自优化控制方法,通过考虑批内变量的因果性,最终得到了具有优化作用的控制律.设计控制系统时,选择被控变量和设计控制器通常是两个独立任务[36],前者主要考虑经济指标的优化,后者关注于如何更好地跟踪控制被控变量,保证控制系统的稳定性和鲁棒性.如何在此前提下求解批内被控变量,仍是一个开放的课题.

本文研究了间歇过程的批内自优化控制问题,贡献如下:1)基于自优化控制策略提出以输出变量的线性组合为被控变量(虚拟变量),在批次运行过程中对其进行跟踪控制,以控制手段实现实时优化;2)根据是否在过程不同阶段切换被控变量,给出了两种自优化控制策略,对每种策略又分别给出了两种设定轨线选取方案;3)引入扩张组合矩阵,将这些情形统一描述为具有不同结构约束的最优组合矩阵求解问题,并推导得到了其中一种方案的解析解计算方法.目前为止,本文所提方法在国内外文献中未见报道.

1 连续过程的自优化控制

对连续化工过程,考虑如下静态优化问题

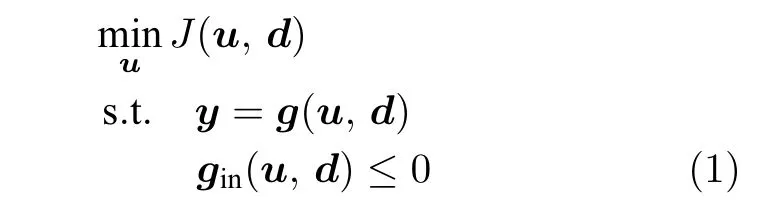
其中,J为经济指标,分别是操纵变量、扰动变量和测量变量,g和gin为输出变量的模型函数和约束条件.

扰动变量d变化且在线不可测是化工过程偏离最优点的主要原因.当扰动变量d变化时,式(1)的解是d的函数,不妨记为uopt(d).实时优化的任务是在d未知的前提下,寻找到新的最优值uopt,实现过程的最优操作.自优化控制(SOC)通过构造虚拟的被控变量c=Hy,当反馈控制器将c控制在恒定设定值cs上时,控制器输出能自动逼近当前的实际最优值uopt(d). 当组合矩阵H每行有且只有一个1,其余为0 时,c为输出变量y的子集,此时退化为传统的以单变量为被控变量的情形.更一般的情况下,H中的非零元素提供了更多优化自由度,可提高系统的闭环经济性能.例如,假设系统自由度nu=2,y=[T P cA]T,包括温度T,压力P和物质A的浓度cA,考虑两种情况:

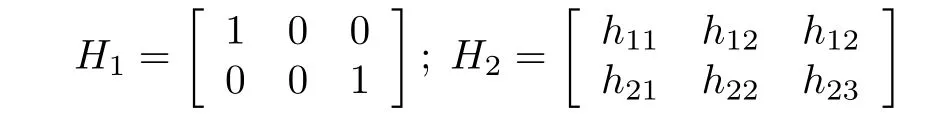
H1对应的被控变量c=H1y为T和cA(单个物理量),H2的被控变量为3 个物理量的线性组合.显然,前者为后者的一种特殊形式.

为求解一般情形的最优组合矩阵H,研究人员针对不同过程特性和衡量标准提出了求解方法[12,28-31].以一种针对线性系统的局部法(Exact local method)为例[28],首先定义损失函数L

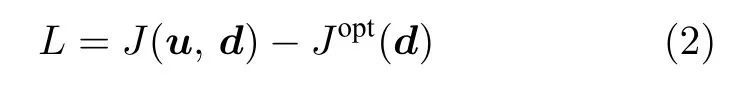
对给定的d,将J(u,d)在最优点uopt处进行二阶泰勒展开

引理1[35].Lav(H)=Lav(QH),其中Q为任意nu维非奇异方阵.

引理1 表明,式(9)的解非唯一(因为控制c=Hy和c=QHy等效).利用该特性,可以先求解出式(9)的一个特解,再推广至通解形式.文献[24]给出了最优H的一个特解,即

2 间歇过程的自优化控制

2.1 间歇过程优化

考虑一类带不确定参数的间歇过程优化问题

对式(11)所示的动态优化问题,通常可以基于数值法将其近似为离散化的非线性规划(Non-linear programming,NLP)问题[37]

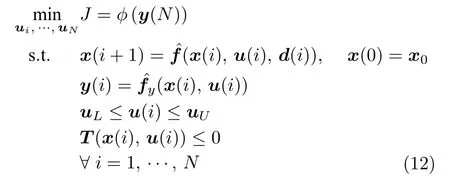
式中,N为间歇过程在操作区间[ 0,tf] 内的离散段数,代表离散后的非线性状态方程和输出方程.

对上述间歇过程的优化问题,文献[27-28]提出了批间自优化控制方法,即构造被控变量c=Hy,利用间歇过程的重复特性逐批次将c控制在恒设定值上.从批间角度看,间歇过程是一个静态过程,因此第1 节中针对连续过程的被控变量求解方法可以较为直接地拓展至间歇过程.但批间优化需要经历若干批次实现被控变量的控制,优化速度较慢.并且,若扰动的变化频率较高(如非重复性扰动),则难以实现被控变量的跟踪控制,优化效果有限.

2.2 批内自优化控制策略

本文研究间歇过程的批内自优化控制方法,即在单批次中控制被控变量实现实时优化.与批间优化相比,批内优化的响应速度更快,能提高优化效果.由于跟踪控制在单批次内完成,批内优化能应对非重复性扰动.对被控变量c=Hy及其设定值cs,考虑如下几种策略:

策略1.H和cs保持恒定;

策略2.H恒定,cs时变;

策略3.H和cs均时变.

策略1 为连续过程中采用的自优化控制方法,对具有时变特性的间歇过程,一般难以取得理想效果.策略2 采用恒定被控变量,其设定值为动态轨线,较策略1 更适合间歇过程.策略3 进一步考虑具有切换结构的控制系统,对离散化的间歇过程,在 [ti,ti+1)时间段内控制一组新的被控变量,如图1 所示.

图1 间歇过程的离散化变量及自优化控制策略Fig.1 Discretization of batch processes and self-optimizing control strategy

结合间歇过程的时变特性,本文主要研究策略2 和策略3的被控变量求解问题.对此,引入如下假设条件:

可以看到,方案1 中被控变量的设定轨线固定不变.而方案2的被控变量设定轨线在当前批次运行过程中不断利用测量值进行修正.相比方案1,方案2 更加充分地利用了过程信息,理论上能进一步提高优化效果,但需求解额外的决策变量H′(i),i=1,···,N.

为推导这两种方案中损失函数与组合矩阵H之间的关系,定义如下超向量

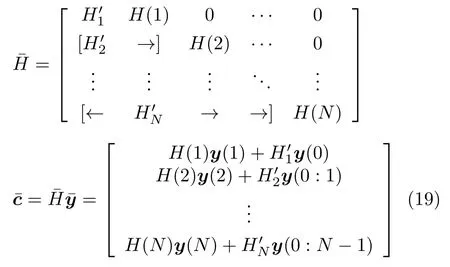
与策略2 相比,策略3 中两种方案的组合矩阵H是时变的,即需求取N个组合矩阵H(i),i=1,···,N.同理,对策略3 求解如下最优化问题

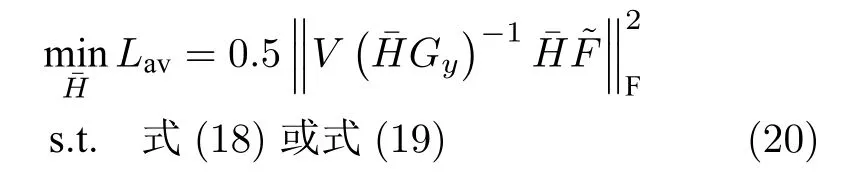
从以上分析看到,对不同的控制策略和设定值选取方案,可以统一归结为具有不同结构的扩张组合矩阵的求解问题,可以在优化问题中对施加等式约束实现.一般来说,具有特定结构的组合矩阵难以求得闭合解,需使用数值优化算法.

注1.以上提出的4 种被控变量选择方案,从控制角度看,执行策略2 (方案1)最简单,但优化效果可能较差;策略3 (方案4)理论上的优化效果最好,但被控变量需要不断切换,并且设定轨线也要在线修正.针对具体过程,需结合过程特性和优化性能结果综合考虑这两个因素,选择最合理的自优化控制方案.

2.3 策略3 (方案4)的解析解

下面提出一种针对策略3 (方案4)的闭合解求解方法.如式(19)所示,此时为块下三角矩阵.为表述方便,将式(19)所示的表达式记为

通过合理利用转化矩阵Q,定理1 将目标函数及约束条件分解到每个离散时间节点,能够沿时间轴依次求解出子矩阵(i). 对∀i=1,···,N,求解如下优化问题

式(26)为带等式约束的二次型凸优化问题,可进一步求得解析解.

定理 2.对式(26)所示的带等式约束的二次型凸优化问题,其闭合解为

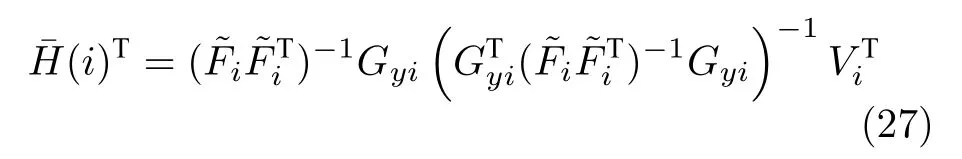
证明.式(26)在形式上与第1 节静态自优化控制问题一致,闭合解(27)的推导过程可参见文献[28].□

综上,本文求取最优扩张组合矩阵的计算步骤如图2 所示,其中策略3 (方案4)可直接应用定理2 求得闭合解,其他3 种情况则需使用数值优化法求取.由于目标函数Lav是的非线性函数,优化问题(17)和(20)不能保证得到全局最优解.对此,策略3 (方案4)得到的解析解可作为数值优化的初始解进行寻优.

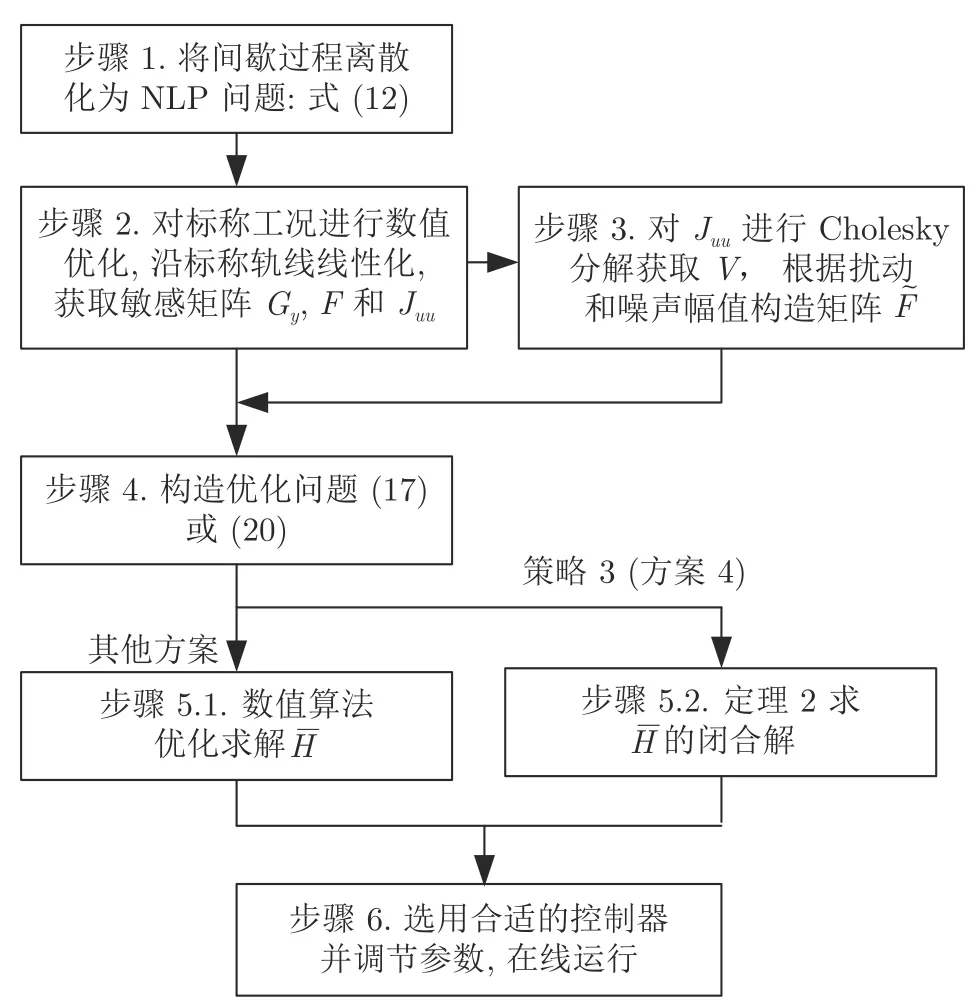
图2 最优扩张组合矩阵 的求解步骤Fig.2 Procedure for solving the optimal extended combination matrix

3 仿真研究

3.1 间歇反应器描述

本节研究一个带副反应的间歇反应器,主副反应分别为A+B →C和 2B →D,其中反应物A在初始时刻投放完毕,B在反应过程中实时投放,实时流量为操纵变量u(t).体系的模型方程为

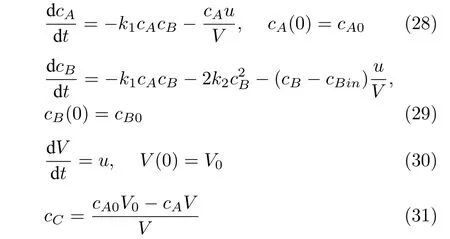
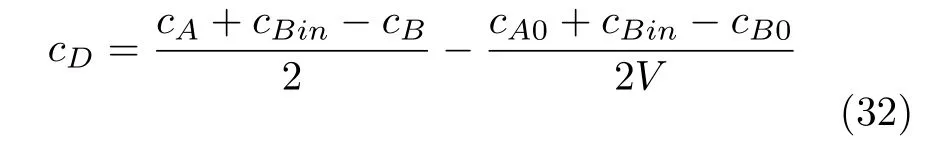
式中,cX表示物料X的浓度,V为持液量,其他符号含义及标称值列于表1.

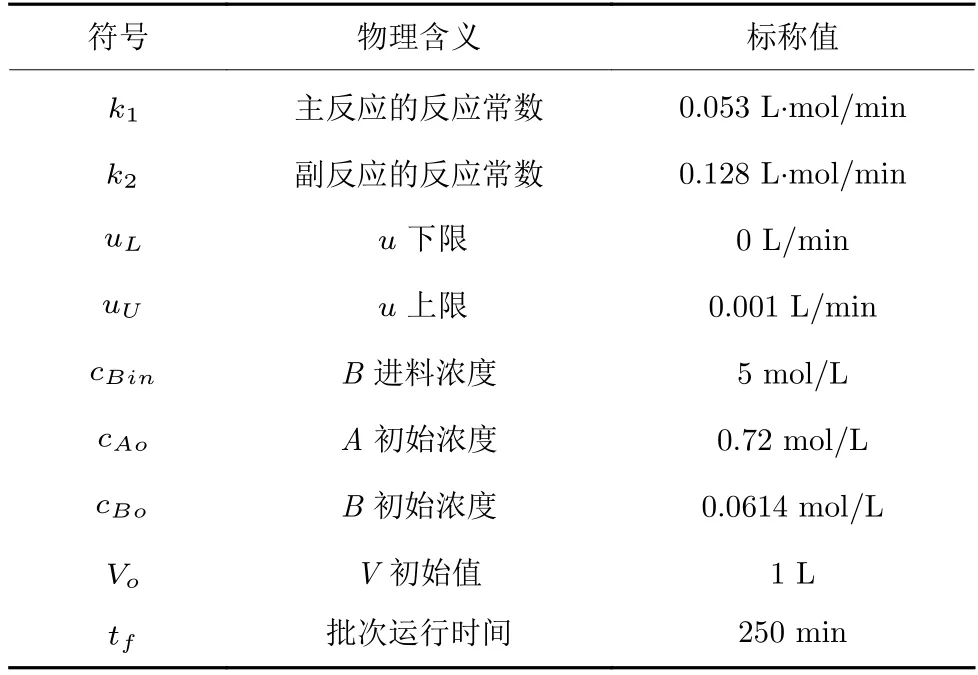
表1 间歇反应器参数及标称值Table 1 Parameters for the reactor model and nominal values

操作目标为在 [ 0,tf] 操作时段内最大化产物产量C的同时减少副产物D,即表示为如下优化问题

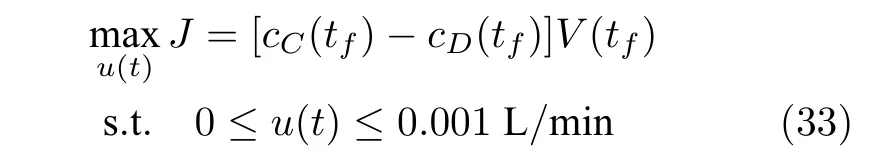
在表1 所示的标称工况下,使用数值优化方法求解式(33)可得到u(t)的最优输入轨迹(图3).可以看到,此时u(t)整个轨线处于可行域内,最优值Jopt=0.271687 mol.反应常数k1和k2为不确定扰动,变化范围为其标称值的±40%.当k1和k2变化时,u(t)的最优输入轨迹随之改变.

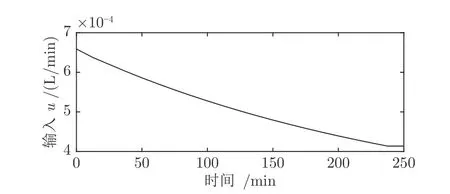
图3 标称点的最优输入轨迹Fig.3 Optimal input trajectory at the nominal point

4 被控变量计算示例

为更清晰地阐述本文方法,以N=2 为例(即[0,tf]被均匀离散为两段),介绍如何使用第2 节中的方法求解不同被控变量.离散后的优化变量个数=2,对式(33)进行重优化后得到Hessian 矩阵和V矩阵

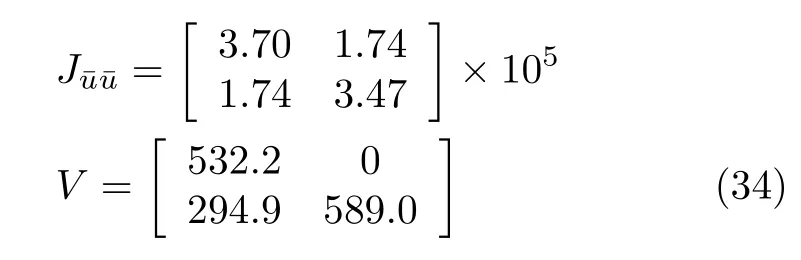
考虑使用cA和cB构造被控变量,对离散系统进行线性化,得到

其中,测量变量=[yT(0)yT(1)yT(2)]为cA、cB分别在0,125 min 及250 min 时刻的量组成.得到上述矩阵后,可以构造式(17)和式(20)所示的优化问题来求解被控变量,结果如下.

1)策略2 (方案1):H=[-0.0026 0.0035],即整个时间段内都控制被控变量c(t)=-0.0026cA+0.0035cB. 经计算,前125 min的设定值为cs(1)=-0.000303,后125 min的设定值为cs(2)=-0.000059.

2)策略2 (方案2):求解得到的扩张组合矩阵为

4.1 批内自优化控制效果

由于N=2 难以逼近整个间歇操作过程,后文设置N=20 并以相同的方法重新求解被控变量,同时,在测量变量中加入体积变量V提高优化效果.从表2 可观察到:

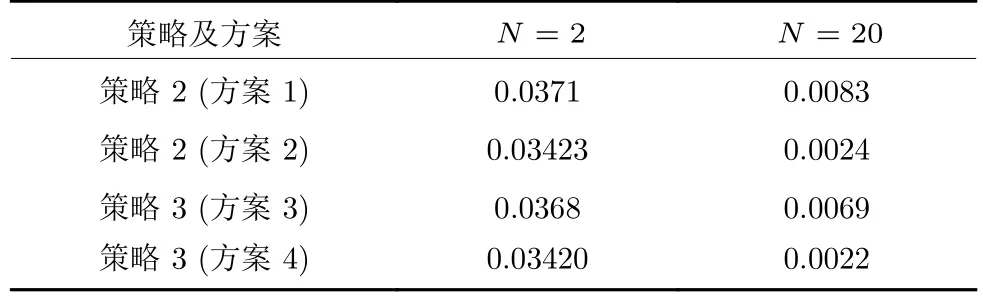
表2 损失函数LavTable 2 Loss functionLav

1)4 种方案的损失Lav在N=20 时,相比N=2都大幅度降低;

2)策略2 (方案1)的损失函数为0.0083,策略2 (方案2)通过在线设定值修正,进一步将损失减少到0.0024;

3)策略3 (方案3)的损失为0.0069,略低于策略2 (方案1);

4)策略2 (方案3)的损失为 0.0024,与策略3(方案4)的损失0.0022 很接近,表明不切换被控变量也能得到较好的优化控制效果.

基于表2的结果,策略2 (方案2)与策略3 (方案4)效果接近,但前者无需在线切换被控变量,更易于在线控制,因此考虑使用策略2 (方案2)对该反应器进行批内自优化控制.此外,动态仿真中将与策略2 (方案1)的结果进行对比,有助于进一步理解本文方法.

策略2 (方案1)的被控变量为c1(t)=0.0062cA+0.002cB+0.0831V,设定值轨线如图4 所示.为进一步获取平滑的设定值轨线,使操作更为平稳,对这些离散点进行回归分析,得到平滑的设定值轨迹方程cs(t)=0.0877+3.705×10-5t-1.97×10-8t2,为一条随时间t变化的连续曲线,如图4 所示.对该系统可以采用普通的PI 控制器对被控变量c1(t)进行跟踪控制.

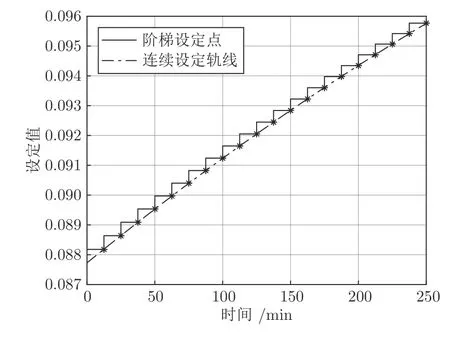
图4 策略2 (方案1)的设定值轨线Fig.4 Setpoint trajectory for Strategy 2 (Scheme 1)

策略2 (方案2)的被控变量为c2(t)=0.0026cA+0.00032cB+0.0830V,设定值轨线在每批次运行过程中采集测量值进行在线修正.为增强操作平稳性,在tk时刻计算得到tk+1时刻的设定点后,在[tk,tk+1]时间段内设置斜坡形设定值轨线,使设定轨线维持连续性.同样使用PI 控制器跟踪控制得到的被控变量c2(t).

不确定参数k1和k2分别改变 +20%和 -20%时的优化控制效果如图5 所示,从图5(a)中可以看到,两种方法分别对c1(t)和c2(t)都实现了较好的闭环跟踪控制,其中,c2(t)的设定轨线根据批内采集到的测量值进行了调整,相比自身的标称轨线有一定程度的上移;图5(b)显示不同方法的控制输入u(t)轨迹,其中,控制c1(t)时的u(t)轨迹相比标称操作更靠近当前工况真实的最优轨线,性能指标J有所提高 (J=0.34374→0.34505),显示出一定的优化控制效果.控制c2(t)时的u(t)轨迹更靠近最优轨线,其性能指标J=0.34701和最优值Jopt=0.34755差别不大.同时注意到控制c2(t)时的u(t)轨迹振荡更加剧烈,这是因为c2(t)的设定轨线不断在线修正,为了得到满意的控制效果,使用了高增益PI 控制器 (Kp=20).这并不影响最终得到满意的优化效果 (L=0.00054),从另一个角度说明了间歇过程中控制关键变量的重要性.

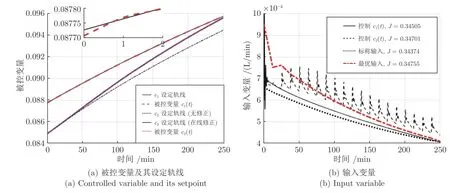
图5 批内自优化控制效果 ( k1 :+20%,k2 :-20%)Fig.5 Within-batch self-optimizing performance ( k1 :+20%,k2 :-20%)

不确定参数k1和k2分别改变 -40%和 +40%时的优化控制效果如图6 所示,此时系统的不确定性向另一个方向变化,并且幅度更大.从图6(a)中可以看到,两种方法同样对c1(t)和c2(t)都实现了较好的闭环跟踪控制,其中,c1(t)的设定轨线不变,而c2(t)的设定轨线相比自身的标称轨线有一定程度的下移.从图6(b)来看,虽然控制c1(t)能将u(t)轨迹向着真实的最优轨线的方向调节,其性能指标J从标称操作的0.09646 提高到0.10312,但作用有限,距离最优值Jopt=0.12252 仍有较大差距.控制c2(t)进一步提高了优化控制效果,其性能指标为J=0.11602,相比最优性能只有0.006的损失(此时k1,k2的变化较大,该损失在一定程度上由系统的非线性导致).此外,控制c2(t)时的u(t)轨迹同样振荡较为剧烈,但随反应进行,u(t)大致围绕着最优轨线上下波动.

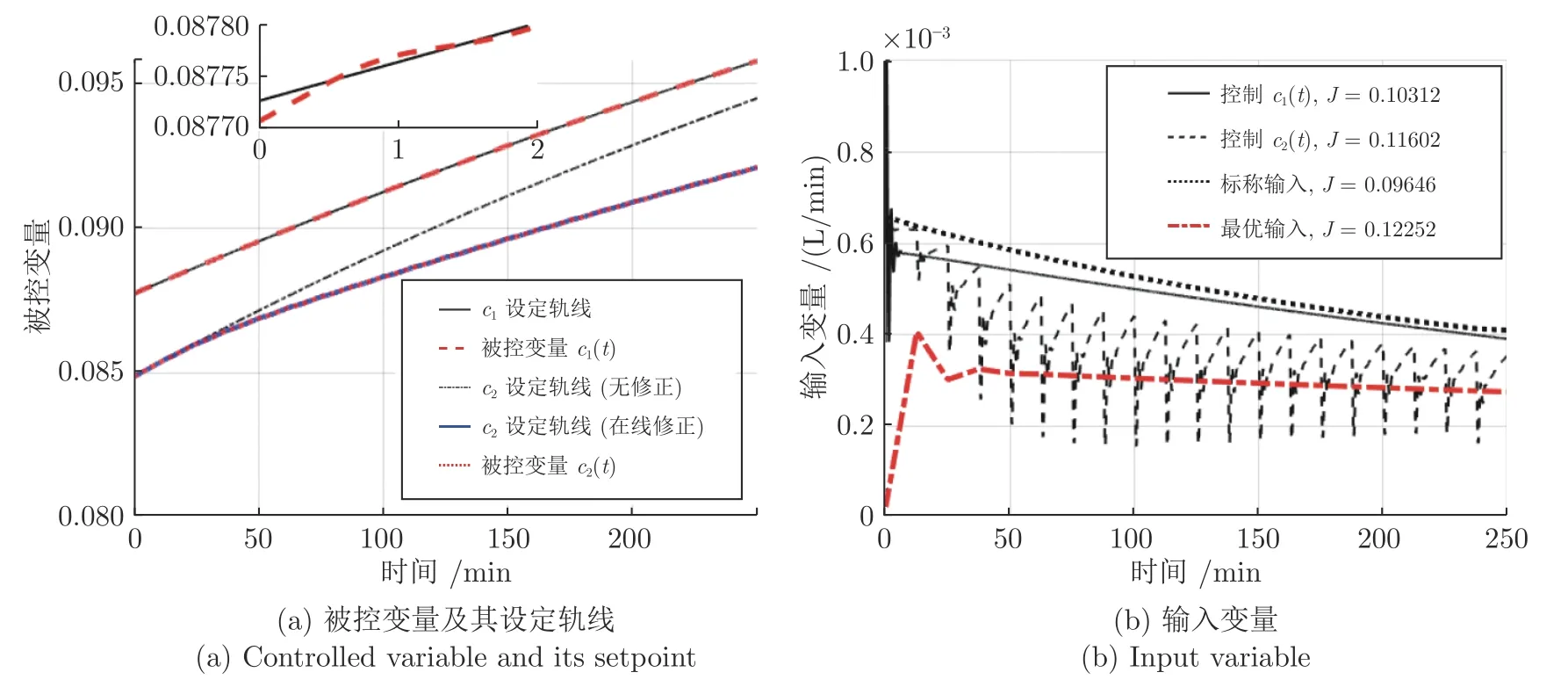
图6 批内自优化控制效果 ( k1 :+40%,k2 :-40%)Fig.6 Within-batch self-optimizing performance ( k1 :+40%,k2 :-40%)

表3 进一步统计了100 组随机扰动下各方法的非线性损失,其中随机扰动 [k1k2] 均匀分布在各自的变化范围.可以看到,相比标称操作(平均损失0.0036)和以单变量cB(平均损失0.0042)为被控变量的情形,两种批内自优化控制方法有效提高了经济性能,其中,策略2 (方案1)中控制c1(t)将平均损失减少到0.0026,策略2 (方案2)中控制c2(t)进一步将平均损失减少到0.0007,几乎可以忽略不计.此外,最大损失和标准差等统计量也呈现出相同的变化趋势,如表3 所示.

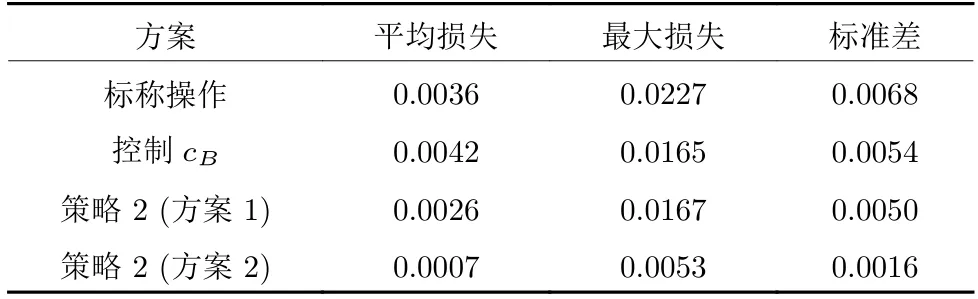
表3 100 组随机扰动下的非线性损失统计量Table 3 Statistics of nonlinear losses for 100 groups of random disturbances

5 结束语

本文研究了间歇过程的批内自优化控制问题,在单批次运行过程中控制一组虚拟的被控变量(输出变量的线性组合),实现间歇过程的实时优化.对此,给出了两种自优化控制策略(被控变量恒定但设定值时变;被控变量和设定值均时变).对它们的设定值选取问题又分别提出两种方案(设定值轨线固定不变;设定值轨线在线修正),共计4 种方法.通过引入扩张组合矩阵,将这4种方法统一描述为具有不同结构约束的最优求解问题,并推导得到了策略3(方案4)的解析解计算方法(定理2).

本文提出的4 种被控变量选择方法,其对应的闭环控制系统具有不同的复杂度和优化性能.针对一般的实际间歇过程,应综合考虑这两个因素并取得合理权衡.间歇反应器的仿真研究中,采用策略2(方案2)(恒定被控变量:c2(t))得到的控制结构较为简单,并且能通过在线修正c2(t)的设定值增强优化效果,是较为合理的方案.