基于WIM的大跨钢箱梁悬索桥疲劳荷载谱研究

贺伟诚，王 超

(湖北工业大学土木建筑与环境学院，湖北 武汉 430068)

大跨度桥梁主梁广泛采用正交异性钢桥面板钢箱梁结构，这种结构具有自重轻、抗扭及横向抗弯刚度大、整体性强、经济性好等优点[1]。然而，由于车轮荷载的反复作用，加之焊接残余应力及初始缺陷的影响，桥梁极易产生疲劳损伤累积，严重时甚至造成结构破坏。针对钢箱梁疲劳损伤问题，研究建立疲劳车辆模型并分析各车型对桥梁疲劳损伤贡献率是重要的方向之一，国内外学者在该领域开展了相关的研究工作。宗周红等[2]研究了京沪高速公路的重车疲劳荷载谱，发现重车占比较高，且六轴二类车型为等效标准疲劳车。胡森林等[3]提出了针对广西地区疲劳设计的疲劳损伤修正系数建议值。王元清等[4]针对建立的车辆荷载模型进行分析，得出42 d样本量可以用来代表整体分布特征的结论。邓扬等[5]、Zhang等[6]研究了分时段的疲劳荷载谱，前者发现晚上超车道的车重均值比白天高，后者发现汀九桥的疲劳寿命在120 a的设计限值内。Yan等[7]研究了中、小跨径桥梁的疲劳应力谱，发现超载控制对于疲劳应力谱中高幅应力的概率密度有很大的影响。翟慕赛等[8]建立了不同等级公路的疲劳荷载谱，发现不同等级公路其疲劳荷载模型也不同。孙秀雅等[9]基于疲劳荷载谱针对坝陵河大桥疲劳易损部位进行了疲劳寿命分析，得出桥上疲劳细节的疲劳寿命高于设计值的结论。陈斌等[10]研究了目标基准期内车辆荷载的极值分布，发现车辆荷载存在离散性大的特点。罗媛等[11]提出了桥梁上基于随机重载车流的疲劳可靠度分析方法，发现车辆轴数多少和桥梁等效疲劳应力幅的高低存在负相关性。刘扬等[12]研究了关于随机车流作用下简支梁桥设计基准期内荷载效应极值概率分布的问题。Deng等[13]建立了疲劳荷载谱并单独讨论了六轴车的车辆模型，提出了一种针对疲劳车辆模型研究的新方法。MulyadiEndang等[14]进行了对比S-N曲线与标称疲劳抗力的研究，得出S-N曲线上50 a寿命依然低于疲劳极限的结论。Guo等[15]利用车辆疲劳荷载谱对桥梁的可靠度进行了分析，发现随着时间的推移和车流量增加，可靠度会加速降低。

我国幅员辽阔，各地环境不同、桥型各异、交通流量状况复杂多变，对于不同地区桥梁特别是特大跨度钢箱梁桥的疲劳问题，有必要针对其实际运营环境进行专门的研究分析[16]。另外，桥梁的实际交通状况会受工作日、节假日、季节变化影响发生改变，为了确保统计得到的疲劳荷载谱更加准确和具有代表性，有必要采用较长时间段的数据进行分析。因此，本文将针对某大跨度正交异性桥面板钢箱梁悬索桥进行疲劳分析，利用动态称重系统(WIM)长期采集的实桥车辆荷载数据进行统计分析，引入确定模型最佳分量数的两种准则，采用混合高斯分布拟合车重数据的分布规律，得到车重概率密度曲线并建立疲劳荷载谱，进而计算出各车型对该桥的疲劳损伤贡献率。

1 车辆荷载数据统计

1.1 工程概况

某大跨度钢箱梁悬索桥是绕城公路的重要组成部分，设计速度为120 km/h，钢箱梁主梁全宽38.5 m，设双向六车道，主梁横断面布置图如图1所示。为了保障大桥的安全运营，大桥建设了桥梁健康监测系统，实时采集包括车辆信息在内的各类桥梁运营期的关键参数。由于此桥地处城市外环，是连接市内外的枢纽，交通量大，车型多样，交通状况复杂，不同车型会对桥梁造成不同程度的疲劳损伤，因此，这里将对该桥WIM系统采集的长期车辆荷载数据进行分析研究。

图1 某钢箱梁悬索桥横断面图 mm

1.2 车型分类

由于实际车辆类型庞杂，没有必要对每一种车型进行统计分析，为了分析简易性和有效性，需要对其进行分类。由于结构疲劳损伤主要由应力幅和循环次数控制，而正交异性桥面板钢箱梁应力幅循环次数主要受轴数影响，这里依据轴数将车辆进行分类，特别是实际交通流中大量存在的各种两轴车都归为一类。另外，车辆荷载与桥梁疲劳寿命成负相关性，过小的车辆荷载对疲劳寿命的影响可忽略不计，为了简化分析，可以先对数据进行预处理，剔除车重过小(小于3 t)的车辆[17]，再进行统计分析，预处理后得到的各典型车型交通量如表1所示。

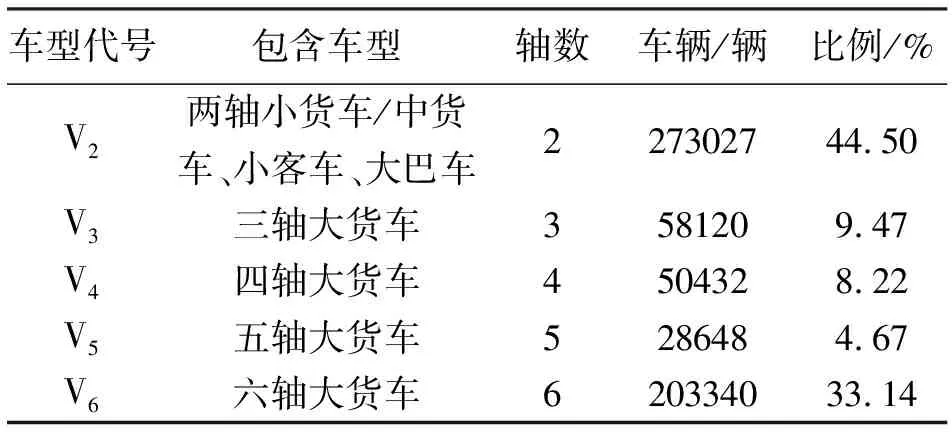
表1 各典型车型交通量

从统计结果可以看出该桥车流量以V2型车即两轴车为主，占到了44.5%，六轴大货车仅次于两轴车，相对占比也比较高，达到33.14%，其他四种车型占比均低于10%。考虑到相对于其他大货车来说，两轴车载重和轴数相对较小，多轴大货车的疲劳影响也不容小视，下文将对此进行详细分析。

1.3 交通量统计

基于表1的典型车辆分类，现统计出每周各车型的车流量情况，由于少部分数据缺失，故共分析了24周的车辆数据，统计的各车型车流量变化如图2所示。从图2a可知各周的车流量变化都比较明显，其中第22周的变化尤为显著，推测可能是桥面检测或维修等原因导致；从图2b可以直观看出各周车流量的构成也存在不同程度的变化，两轴车和六轴车占比变化更为突出，并且两类车占比趋势基本相反。

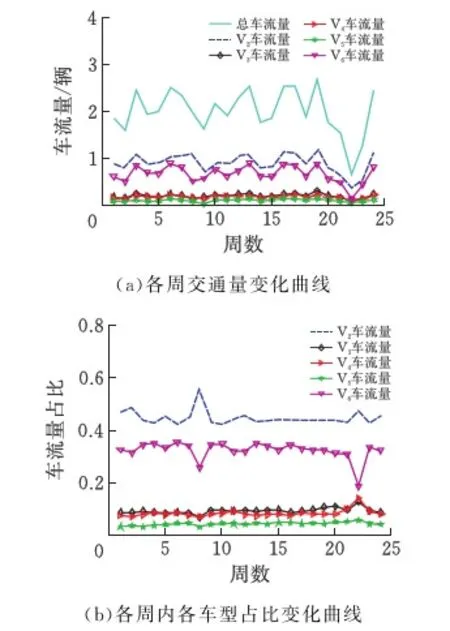
图2 交通量变化

由于不同车型及车重的车流量每周变化明显，需要采用较长时间的监测数据统计分析车流荷载分布特征，才能减少因偶然性而导致数据出现过大或过小的情况发生，从而确保建立的疲劳荷载谱更加准确并且具有代表性。

2 模型车辆疲劳荷载谱

2.1 车重统计

基于表1的交通量统计，再依据各类型车车重数据即可统计得到各车型的车重分布特征。以V2车型为例，根据实测数据统计其车重分布如图3所示。这里将根据车重分布图拟合其概率密度曲线，由图3可以看出，车重分布图呈现出多峰的形式，普通正态分布(图中虚线)很难较好地拟合其分布特征，拟采用混合高斯分布拟合该分布规律，其概率密度函数如式(1)：

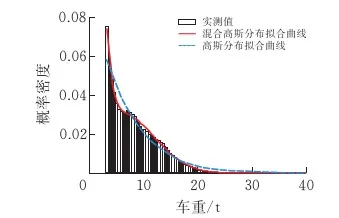
图3 二轴车的车重-概率密度及拟合曲线

(1)

式中：M为分量数，描述分布峰值个数；Pi为各分布型对应的系数；fi(x)为各高斯分布的概率密度函数。

采用混合高斯分布拟合需要确定拟合曲线的高斯分量数，当分量数过小时，其拟合效果较差，分量数过多又会使问题变复杂，对于解决实际工程问题收效不大。为了更加准确描述概率分布情况，这里引入赤池信息准则(AIC)和贝叶斯信息准则(BIC)来优化确定最佳分量数，AIC和BIC分别定义为式(2)和(3)：

AIC=-2lnL+2M

(2)

BIC=-2lnL+MlnN

(3)

(4)

式中：M为分量数；lnL为模型的对数极大似然函数值；N为模型中数据的个数；SSE为残差平方和，具体见式(5)。

模型最佳分量数的选取应优先考虑AIC值，取AIC最小时对应的M值；而当AIC值相差不大时，则引入BIC，最优分量数依旧取其值最小时对应的M值。

对于概率密度函数拟合的效果，采用拟合函数的SSE(和方差)以及R2(确定系数)进行评估，其定义为：

(5)

(6)

拟合曲线的和方差值越接近0，确定系数越接近1，则拟合效果越好。

针对图3所示的V2型车，计算出采用不同分量数的混合高斯分布拟合车重概率分布时对应的AIC和BIC值，如图4所示。

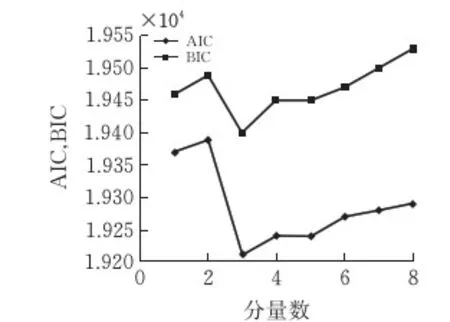
图4 V2型车混合分布模型信息准则值变化曲线

由图可见，当分量数为3时，AIC和BIC的值均达到最小，故V2型车多峰分布模型的分量数M取3。相应的混合高斯分布拟合曲线如图3中红线所示。

为了检验实测值的统计规律和拟合曲线之间的契合度，可求解出拟合函数的SSE(和方差)以及R2(确定系数)，其拟合优度如表2所示。

从统计结果可以看出，V2型车数量最多，车型复杂，但整体而言车重量都不大，基本在6～13 t之间。采用同样的方法，对其他四种车型的车重进行统计，具体统计结果如图5所示，可以发现三轴车和四轴车的车重分别为10.64 t和14.55 t时概率密度均达到最大峰值，且三轴车和四轴车分布规律类似，均出现峰与峰之间距离过大的情况，最右的一个峰其峰值较低，此峰值表明存在部分车辆满载或超载；五轴车和六轴车均呈现为双峰，两类车型的车重分别为16.39 t和17.98 t时概率密度达到最大峰值。而用于拟合各车型车重概率分布的分量数、拟合曲线的参数以及拟合优度等参数可见表2。

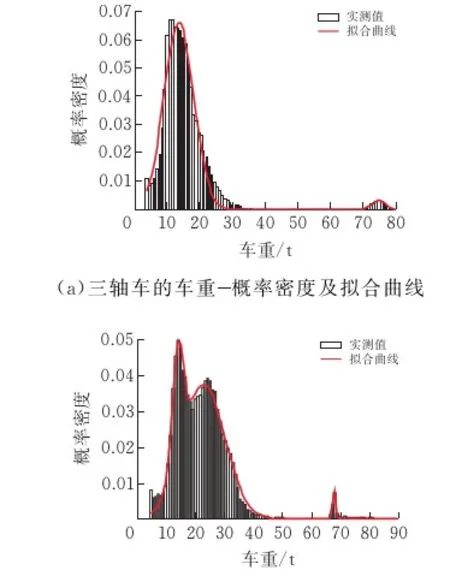
图5 各车型车重概率密度模型

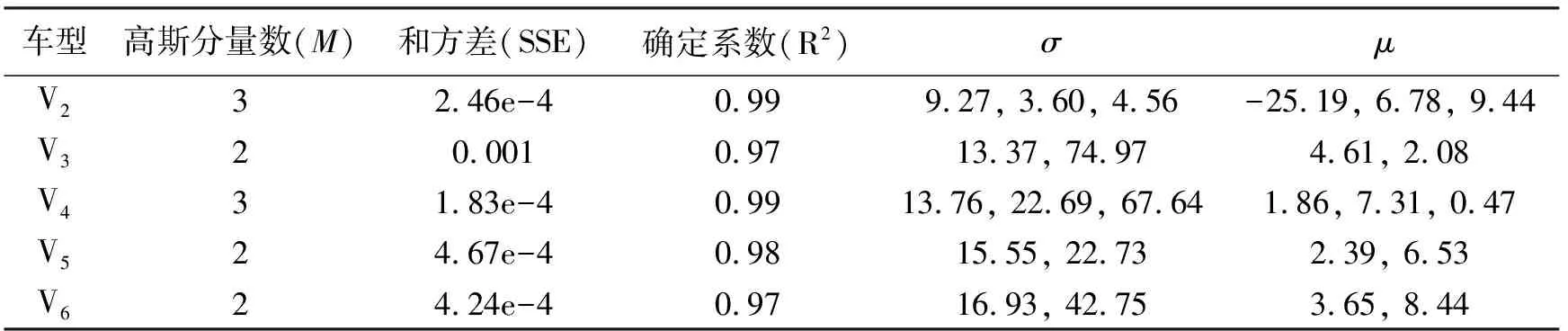
表2 各类车型车重概率密度曲线拟合参数及拟合优度

由表2各车型概率密度拟合曲线的和方差以及确定系数可知，五种车型混合高斯分布的和方差均接近于0，确定系数均大于0.96，由此可以确定混合高斯分布能较好拟合各车型的概率密度曲线。

2.2 建立疲劳荷载谱

依据Miner线性积伤率和等效疲劳损伤原理，当累计疲劳损伤相同时，可以将i个不同车重作用1次视为1个等效车重作用i次，等效车重计算式如下：

(7)

式中：W(eq)k为第k种车型的等效车重；pi为第k种车型中i车出现的频率；Wi为该车车重。

将原始数据中每种车型的各轴重分别统计，计算各轴重在车重的占比，即可得到各车型轴重分配系数γk，计算方法如式(8)所示，表3为各车型轴重分配系数。

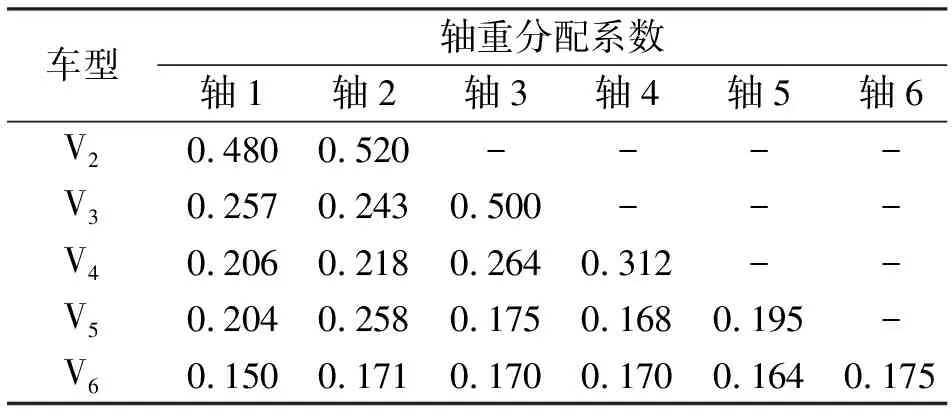
表3 各车型轴重分配系数

(8)

式中：γk为第k种车型的轴重分配系数；ω(eq)k,j为第k种车型第j轴的等效轴重；W(eq)k为第k种车型的等效车重。

运用式(7)计算出等效车重后，再结合轴重分配系数即可得到各车型的等效轴重数据，然后建立车辆的疲劳荷载谱，见表4。

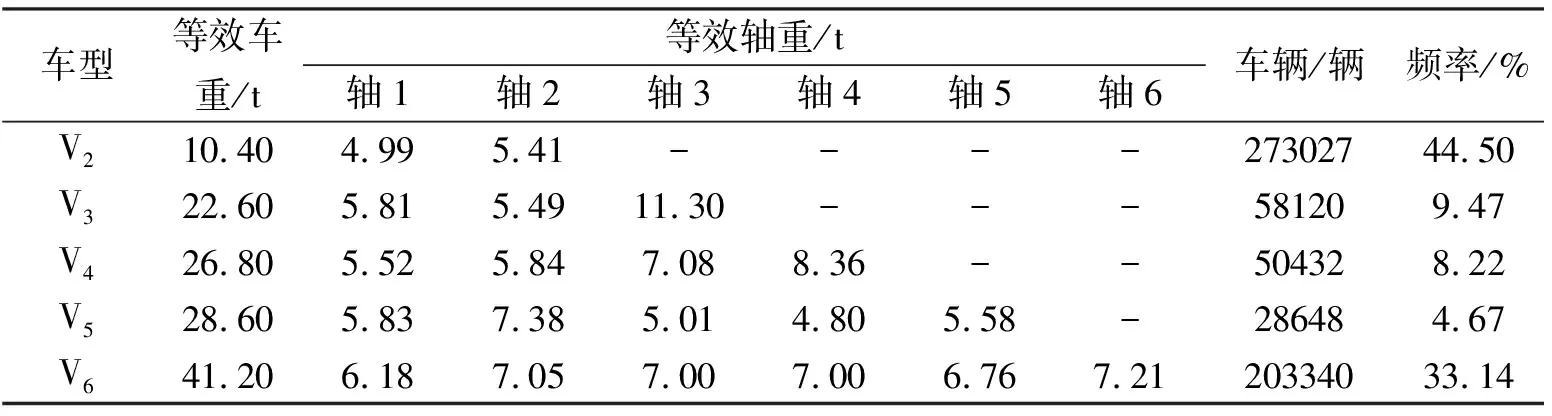
表4 疲劳荷载谱

3 疲劳损伤贡献率

桥梁结构的疲劳损伤性能可以由不同车辆对桥梁产生的疲劳损伤贡献率来反映，各车型对结构产生的损伤值和疲劳损伤贡献率根据上文统计的车辆疲劳荷载谱来计算。对于正交异性桥面板钢箱梁，桥面板钢结构在车辆局部荷载作用下应力影响线很短[18]，局部效应比较明显，所以结构疲劳损伤与轴重直接相关，可以通过计算等效轴重的疲劳贡献率再结合轴数来得到等效车重的疲劳贡献率。具体计算方法如下：

第k种车型第j轴等效轴重造成的桥梁损伤值D(eq)k,j为：

(9)

式中，c为结构或材料的性能参数；β为轴重引起的应力幅值系数；m为S-N曲线的斜率负倒数，取m=3；nk,j为第k种车型第j轴的总轴数；ω(eq)k,j为第k种车型第j轴的等效轴重。

各轴产生的总疲劳损伤值D为：

(10)

式中，kmax为车型总数；jmax为第k种车型的最大轴数。

第k种车型第j轴等效轴重造成的疲劳损伤贡献率为：

(11)

第k种车型的疲劳损伤贡献率λk定义为：

(12)

由此可以计算得到各轴及各车型对桥梁造成的疲劳损伤贡献率，如表5所示。

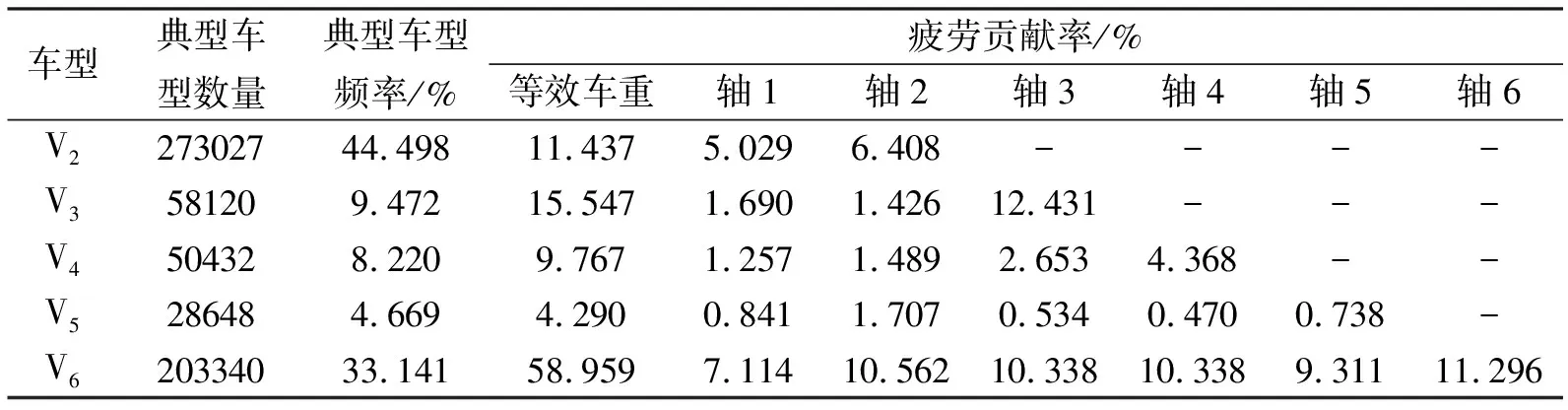
表5 各轴及各车型的疲劳贡献率

从表5数据可以看出：1)两轴车的频率在各类型车中最大，但六轴车等效车重和各轴等效轴重产生的疲劳贡献率最高，原因是在疲劳损伤贡献率的计算中等效轴重的权重高于车辆数，并且六轴车的轴数最多、该车型各轴等效轴重相比于其它车型也较高；2)两轴车频率远远高于三轴车，但等效车重产生的疲劳损伤贡献率却略低于三轴车，原因是虽然这两类车型的轴1和轴2等效轴重相差不大，但三轴车的第3轴的等效轴重远高于两轴车的所有轴重；3)四轴车和五轴车的频率本身较低，并且各轴等效轴重都不高，最终产生的疲劳损伤贡献率都较低。

4 结论

通过对某正交异性桥面板钢箱梁桥动态称重系统长期监测的车辆荷载数据进行统计分析，采用混合高斯模型拟合车重荷载分布概率密度，建立了该桥的疲劳车辆荷载谱，最后分析研究了各车型对该桥的疲劳损伤贡献率，分析结果表明：

1)基于长时间的数据采集和分析，发现各周的车流量变化显著，每周车流量的车型构成也有很大变化，其中两轴车和六轴车占比变化最明显，且这两类型车的占比趋势基本相反。长期的统计数据可以减小偶然因素带来的影响，从而使研究更具有代表性和普遍性，所以有必要对长期车流情况进行研究。

2)各车型的车重概率密度分布均服从混合高斯分布，且由赤池信息准则和贝叶斯信息准则确定高斯分量数后的拟合曲线其和方差均接近于0，确定系数均大于0.96，可知拟合效果较好。

3)通过建立各车型疲劳荷载谱可知，V3型车第3轴的等效轴重与各类车型的等效轴重相比都最大，除此之外的各车型等效轴重相差都不明显，但是随着轴数的增加，等效车重也随之增大，所以V2型车等效车重最小，V6型车最大。

4)六轴车各等效轴重产生的总疲劳损伤贡献率最高，三轴车其次，两轴车仅次于三轴车，四轴车和五轴车最低。原因是六轴车频率较高，各轴的等效轴重也较大，且轴数多，再加上等效轴重相比于车流量更加影响疲劳损伤贡献率的计算，导致疲劳损伤贡献率最高和最不利车型都是六轴车。