粗糙曲面无摩擦接触下的亚表面裂纹扩展分散性研究

周炜，罗柏瑶，唐进元

（1.湖南科技大学难加工材料高效精密加工湖南省重点实验室，湖南湘潭 411201；2.中南大学高性能复杂零件制造国家重点实验室，长沙 410083）

机械加工过程在零件表面生成的几何形貌包含诸多波长成分。虽未见严格定义，但通常将波距在1 mm 以下的表面轮廓成分界定为粗糙度[1]。界面之间诸如力与运动的传递，皆是通过粗糙度微凸体之间的接触来实现，粗糙度对机械零件表面接触[2-3]与疲劳性能[4-5]的影响不言而喻。为实现定量描述与评判，提出了许多粗糙度参数以作表征[6]。有效地建立粗糙度参数与接触疲劳性能之间的关联，对指导微观几何结构设计及其创成大有裨益。

有别于光滑界面几何的确定与规则性，粗糙度形貌具有随机与无序特征，这给微观尺度形性关联研究提出了挑战。一方面，粗糙度参数众多，哪些表征参数与接触疲劳性能相关尚未形成定论。另一方面，同一表征参数下接触疲劳性能不是一个确定值，而是在一定范围之内变化，呈现出较大分散性[7]，这种分散程度取决于粗糙度形貌的随机特征。因此，研究粗糙度随机特征与接触疲劳性能分散性大小之间的关联机制，揭示对接触疲劳性能分散性起主导作用的粗糙度结构特征，对于提升抗接触疲劳设计的一致性，具有有益参考价值。

在粗糙度形貌建模方面，试验测试手段提供了一种可靠解决方案[8]，不过限于试验成本和形貌样本的不可控性，从理论上寻求更为高效的重构方法意义显见。分形理论[9]和Motif 方法[10]从不同视角带来了研究契机，但相关理论尚待完善，因此应用受到局限。相较而言，将粗糙度视为平稳随机过程的统计理论与方法[11-12]发展成熟且直观简明，基于此的粗糙表面性能分析正方兴未艾，对粗糙度参数之间[13-14]、粗糙度与接触疲劳性能之间[15-16]关联进行了有益探索。

得益于摩擦学测算手段的进步，粗糙表面性能预测取得了长足进展[2-3]，但在亚表面疲劳损伤机制研究方面尚未形成有效共识。尽管这方面研究工作并不鲜见[17]，但大多聚焦于宏观几何[18]与裂纹[19]、加工纹理[20]与伤痕[21]、材料组织结构[22]等方面。粗糙度与亚表面裂纹扩展损伤的关联规律还不明晰，特别是粗糙度的随机特征如何映射于疲劳裂纹演化过程中的分散性尚不明确。

针对工程中常见曲面接触零件，如齿轮、轴承和轮轨等，暂不考虑摩擦作用，研究粗糙度随机效应下亚表面裂纹扩展分散性。为此，借助FFT粗糙表面重构方法对不同统计分布下的粗糙度形貌进行仿真，应用弹性接触数值计算方法对仿真形貌样本开展粗糙曲面接触分析，再以计算所得接触压力分布为输入，基于线弹性接触力学和扩展有限元法计算亚表面裂纹在不同曲率半径和外载下的扩展路径与寿命，探究粗糙度统计分布参数与裂纹扩展分散性的内在关联。

1 方法与原理

1.1 粗糙度形貌重构

工程表面粗糙度形貌近似满足如下高斯高度分布与幂指数衰减型自相关分布，即：

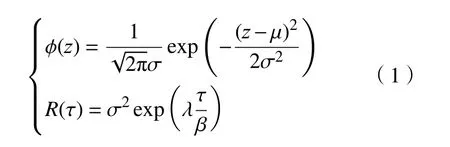
式中：z 为粗糙度采样高度；μ、σ 和 φ分别为采样高度序列[z]均值、标准偏差和概率密度分布函数；R、τ、λ和β 分别为自相关性、滞后距离、高通滤波常数和相关长度。考虑到自相关分布衰减时的波动，将R衰减为原点值1/10时的滞后距离定义为相关长度（又称衰减长度），此时λ=-2.3。可见，粗糙度形貌主要取决于标准偏差σ 和相关长度β。

为重构出给定统计分布（σ，β）下的粗糙度形貌，由伪随机数发生器生成标准偏差为σ 的高斯白噪声[ε]，对高斯白噪声和滤波系数[h]进行卷积，得到高度序列[z]，即：

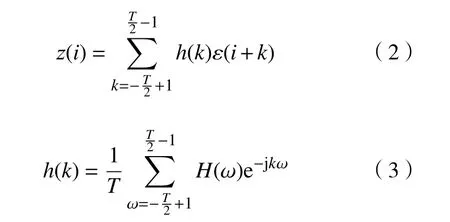
式中H 为h的傅里叶变换。

自相关分布R（τ）可由[z]计算得到，即

为确定H，对R做傅里叶变换，有

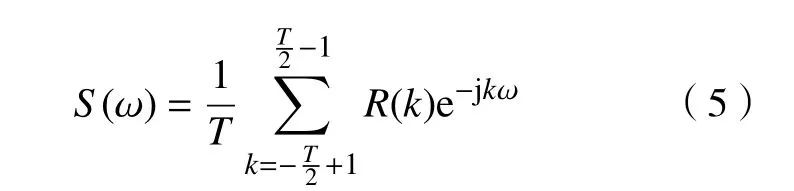
式中ω =-T/2+1,···,T/2-1。

由式（2）和式（4），可得

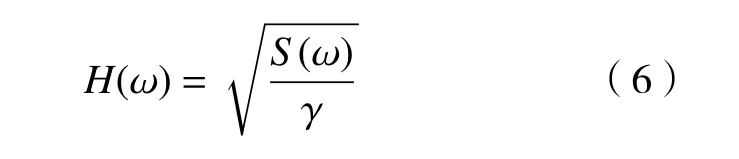
式中γ 为高斯白噪声功率谱密度所确定的常数。

1.2 粗糙曲面接触分析

粗糙曲面接触如图1所示，其可等效为刚性平面与一等效粗糙曲面之间接触，如图2所示。

7.2.8 疼痛的评价 可以采用Wong‐Baker疼痛评价图谱［18‐19］，或视觉模拟评分（VAS）。

图1 粗糙曲面接触示意图

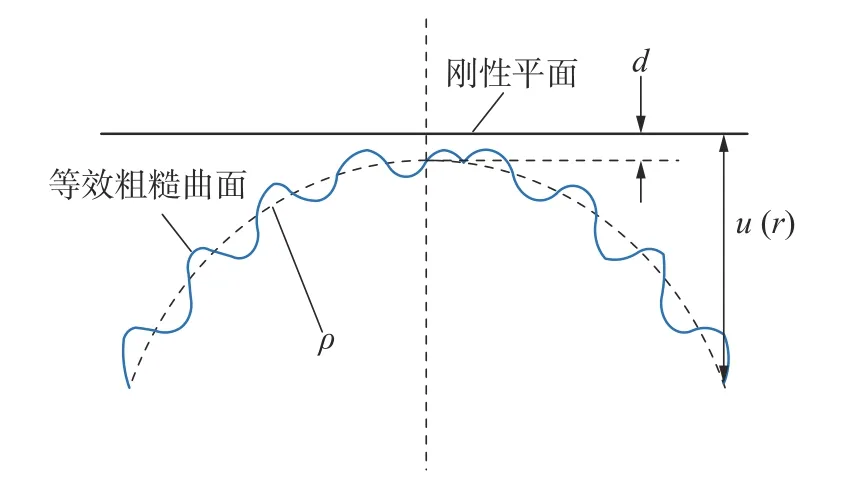
图2 刚性平面与等效粗糙曲面接触示意图

假设两接触体曲率半径分别为ρ1和ρ2，粗糙度分别为σ1和σ2，弹性模量分别为E1和E2，泊松比分别为ν1和ν2，则等效粗糙曲面综合曲率半径ρ和弹性模量E*为：

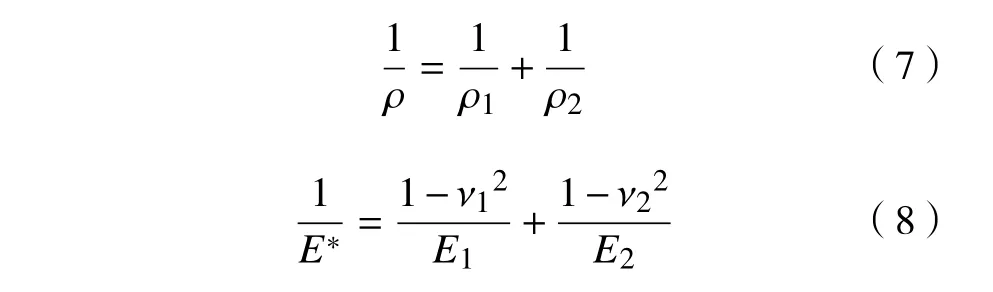
为求得等效粗糙曲面上接触压力分布，利用半无限大平面弹性理论，由Flamant 压力-位移关系建立接触控制方程。对于图3所示矩形压力单元p，在距x′处一点产生弹性位移uz为

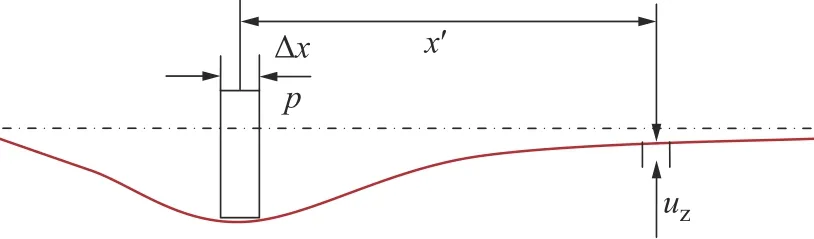
图3 压力-位移关系示意图

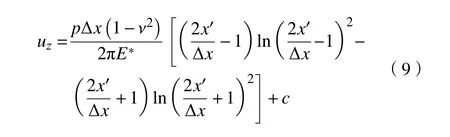
式中：Δx 为压力单元宽度；c 为定义相对位移的任意常数。

假定刚性平面与等效粗糙曲面初始间隙为d，在外载W 作用下两物体相互靠近发生干涉δ。依据接触不可穿透条件，则

此外，接触压力满足力平衡条件，有

1.3 裂纹扩展计算

图4 应力计算模型示意图

以粗糙曲面接触压力分布为输入，亚表面应力场根据图4所示模型计算可得：

由于正应力与切应力共存，亚表面裂纹为I型、II型复合型裂纹。依据最大周向拉应力准则，裂纹沿最大周向拉应力方向扩展至失稳断裂，扩展角度ϑ 和等效应力强度因子Keq分别为：

式中：应力强度因子KI、KII由裂尖应力场经相互作用积分确定。

应用Paris公式，得到裂纹扩展速率与应力强度因子幅度关系为

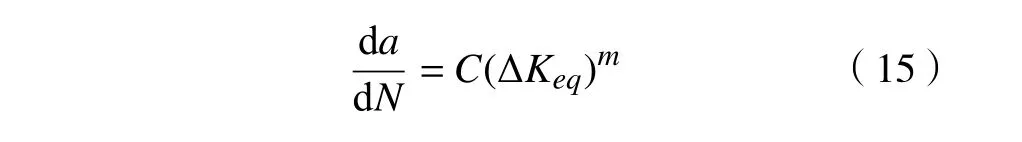
式中：a为裂纹长度；N 为裂纹扩展寿命；C、m为试验确定系数；对于接触下的脉动循环加载，ΔKeq= Kmax。

2 结果与讨论

2.1 裂纹扩展计算程序验证

基于上述原理与方法，利用Fortran 语言开发了二维裂纹扩展计算的扩展有限元程序包，利用已报道文献结果作对比验证。有关计算模型与参数参看NASA报告[23]，所得裂纹扩展路径与扩展寿命对比见图5。其中，FRANC- P1、FRANC-P2、FRANC-P3为不同初始裂纹位置下NASA 报告裂纹扩展路径以及对应初始裂纹位置下，NASA 模型导入FRANC软件计算所得裂纹扩展寿命。pgm-P1、pgm-P2和pgm-P3为相同初始裂纹位置下，本文所开发程序计算所得裂纹扩展路径与扩展寿命。可见，两者吻合较好，验证了本文所开发程序用于I型、II型复合型裂纹扩展计算的有效性。

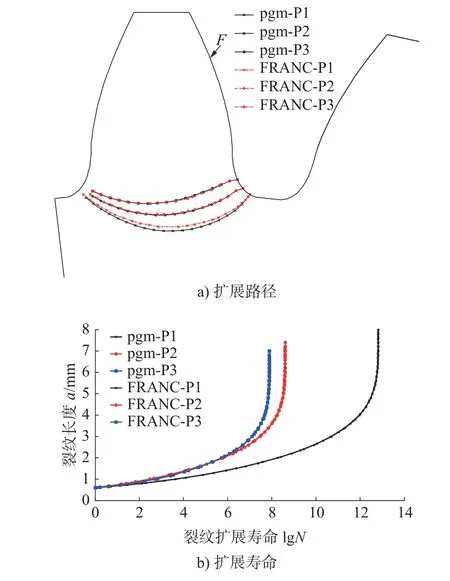
图5 裂纹扩展计算对比

2.2 裂纹扩展变化规律

由于随机效应，同一统计分布（σ，β）下粗糙度形貌千变万化，由其求解所得接触压力分布也呈现随机变化，这将导致后续预测的亚表面裂纹扩展过程彼此存在差异，即裂纹扩展过程表现出分散性。为研究粗糙度统计分布参数对裂纹扩展分散性的影响，同一统计分布（σ，β）下随机重构5个粗糙度形貌样本，由刚性平面与粗糙曲面接触模型计算各样本的接触压力分布，再以接触压力分布为输入，由前述裂纹扩展计算程序包计算各样本的裂纹扩展路径与寿命。图6展示了σ=0.1，β=50时的其中两个形貌样本及其所得接触压力分布。裂纹扩展计算模型如图7所示，其中初始裂纹长度和深度分别为0.1 mm和0.5 mm。计算参数如下：弹性模量为2.11×105MPa；泊松比为0.3；Paris指数m=2.954；Paris系数C =3.124×10-13。

图7 裂纹扩展计算模型

不同曲率半径下，外载W =0.5 N/μm，相关长度β =50，标准偏差σ =0.1、1及光滑曲面下裂纹扩展路径与寿命见图8，其中max 和min 表示相同统计分布下5个形貌样本计算结果的最大和最小值。相比于光滑曲面，标准偏差越大，裂纹扩展路径和寿命越分散。整体而言，裂纹扩展越深、横向扩展越广，则发生断裂时材料脱落的区域越大，与之对应的寿命也越长。曲率半径ρ= 5000μm 时，裂纹扩展路径深度和广度都最大，其平均寿命最长，但此时寿命分散性也最大。曲率半径ρ= ∞时，裂纹扩展路径最浅、横向分布也最窄，其平均寿命最小。可见，曲率半径对裂纹扩展有很大影响，这种影响还体现在标准偏差与裂纹扩展关联之上。随着曲率半径增大，标准偏差引起的裂纹扩展路径分散程度加剧。不同曲率半径下，标准偏差对裂纹扩展深度与广度的影响规律亦有所不同。在ρ= 500 μm 和ρ= 5000μm时，增大标准偏差使得裂纹扩展路径变浅、横向变窄。在ρ= ∞时，增大标准偏差则使得裂纹扩展路径变深、横向变广。可以预见，当曲率半径增至一定程度，增大标准偏差将使得裂纹扩展路径分布在较光滑曲面结果更深、横向更广的区域内。

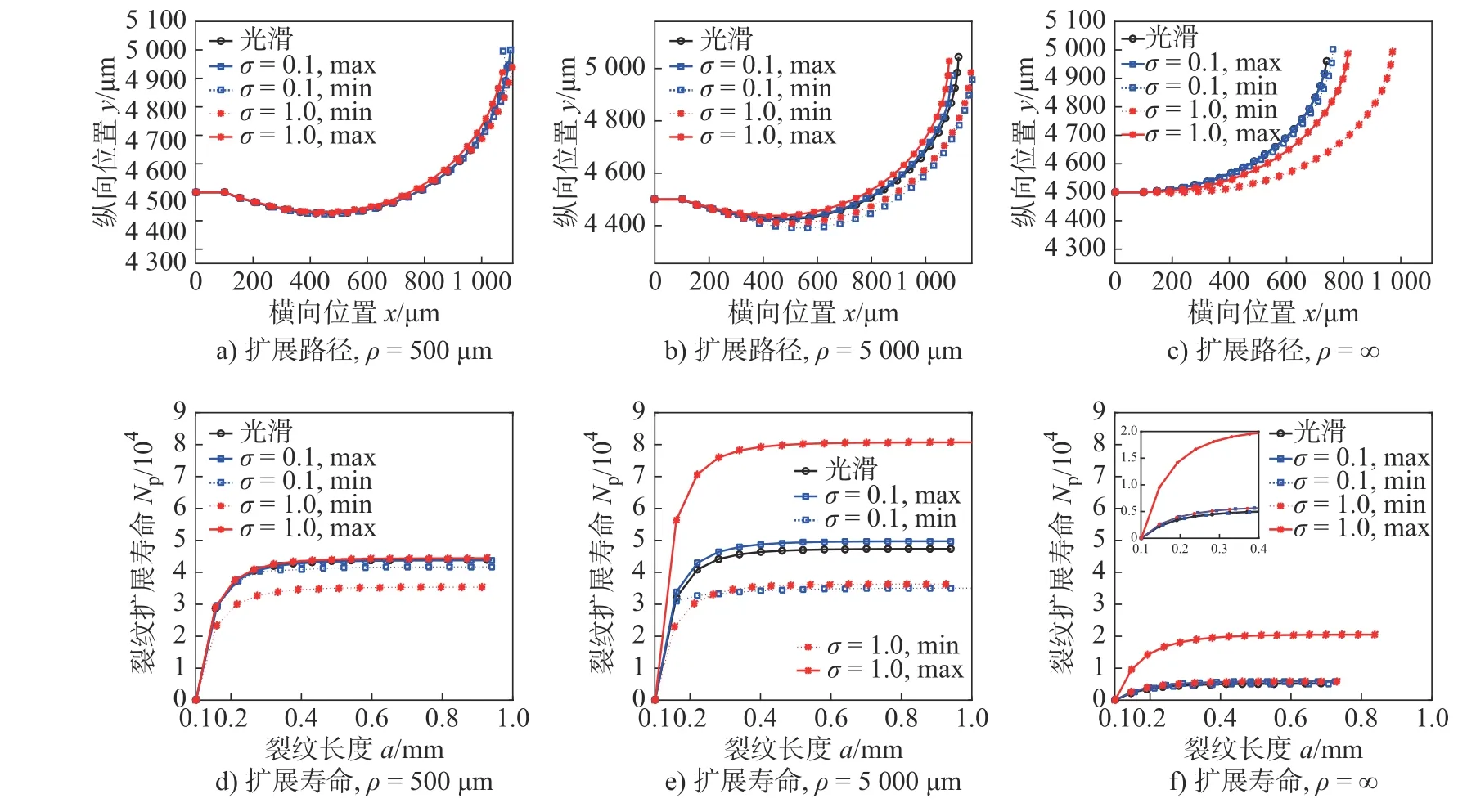
图8 裂纹扩展随标准偏差分布

此外，在ρ= 500μm 时，增大标准偏差使得裂纹扩展平均寿命减小，粗糙曲面裂纹扩展平均寿命明显小于光滑曲面结果。随着曲率半径增大，增大标准偏差使得裂纹扩展平均寿命增大，且粗糙曲面裂纹扩展平均寿命将大于光滑曲面结果。

不同曲率半径下，外载W =0.5 N/μm，标准偏差σ =0.5，相关长度β =0（高斯白噪声）、50、100下裂纹扩展路径与寿命见图9。相关长度与裂纹扩展路径和寿命之间没有表现出显著关联。曲率半径ρ =500μm 和ρ=5000μm 时，3种相关长度下裂纹扩展路径分布范围大体一致，裂纹扩展平均寿命按β =100、β = 0和β =50的次序递减。与此不同，在ρ=∞时，相关长度β =50明显较其它相关长度下裂纹扩展更深、横向更宽广，裂纹扩展平均寿命也最长。裂纹扩展寿命分散性在ρ=5000μm 时仍呈现最大，在ρ=∞时最小。

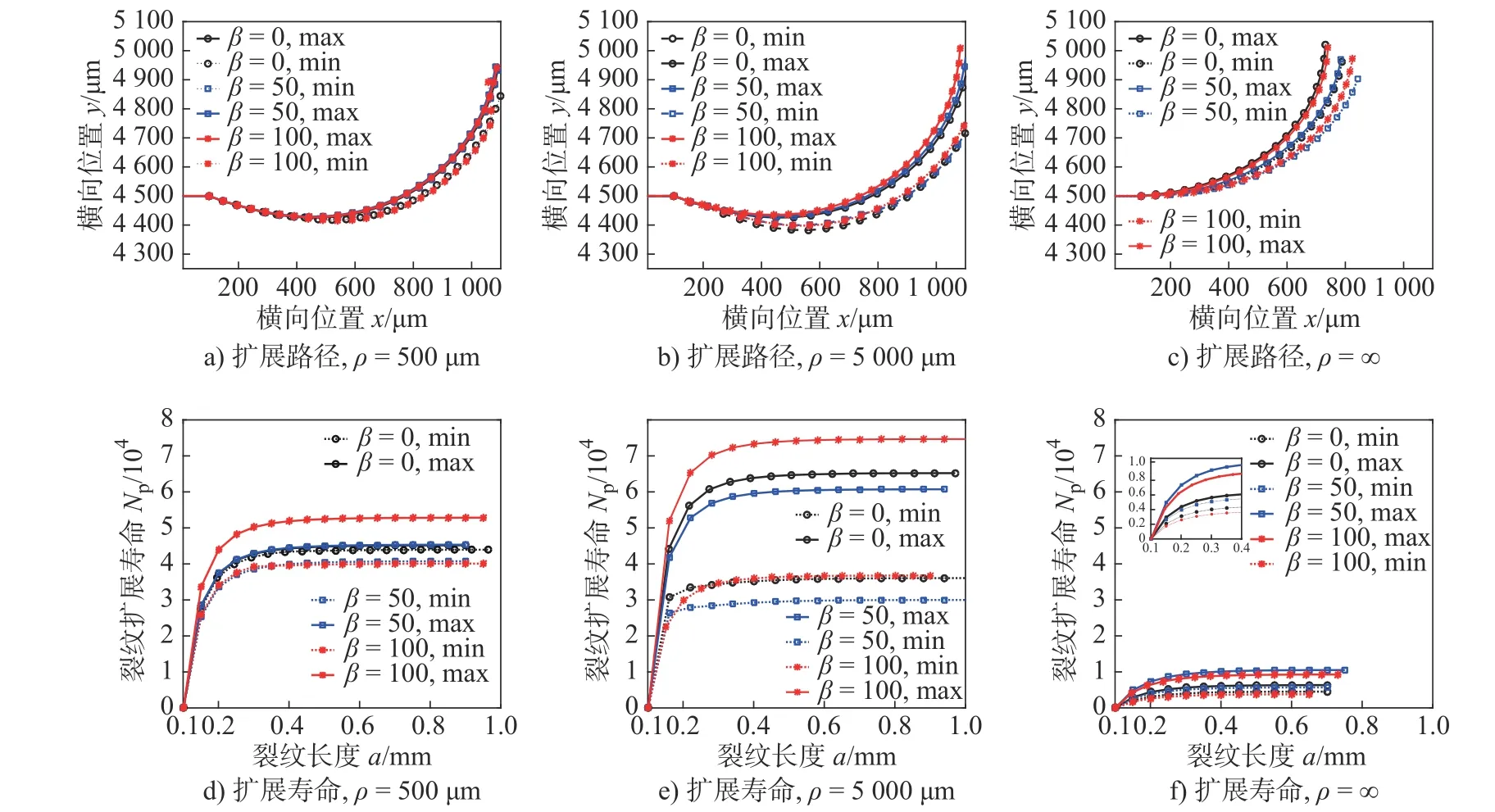
图9 裂纹扩展随相关长度分布

不同曲率半径下，标准偏差σ =0.5，相关长度β =50，外载W =0.1、0.5和1 N/μm 下裂纹扩展路径与部分寿命见图10，其中W =0.1N/μm 时因裂纹扩展速率较慢未给出其寿命。可以清楚地看到，外载越大，裂纹扩展分散性明显减小，且裂纹扩展深度和广度都越小、裂纹扩展平均寿命越短。

图10 裂纹扩展随外载分布

2.3 讨论

由于粗糙度形貌具有随机与无序特征，在其统计分布相同条件下，基于不同形貌样本计算所得裂纹扩展结果分散在一定范围之内，如图11所示，其定量比较列见表1。相比于裂纹扩展寿命，裂纹扩展路径分散程度更小。由前述讨论可知，这种分散性受曲率半径和外载的综合作用。曲率半径ρ=∞时，曲面局部可视为平面，粗糙度的分散性效应被真实地体现，不受曲面影响。随着曲率半径减小，粗糙度作用被曲面逐渐稀释，裂纹扩展随之表现出不同分散程度。较ρ= 5000μm 而言，ρ= 500μm 时曲面曲率很大，粗糙度效应被充分稀释，因此裂纹扩展分散性较小。相反，当曲率半径增大到一定程度，如ρ= 5000μm，粗糙曲面分散效应明显增强。此外，ρ= 5000μm 时得到了具有最长扩展寿命的形貌样本，这表明对于一定粗糙度形貌，可能存在最佳曲率半径，使得裂纹扩展寿命最长。

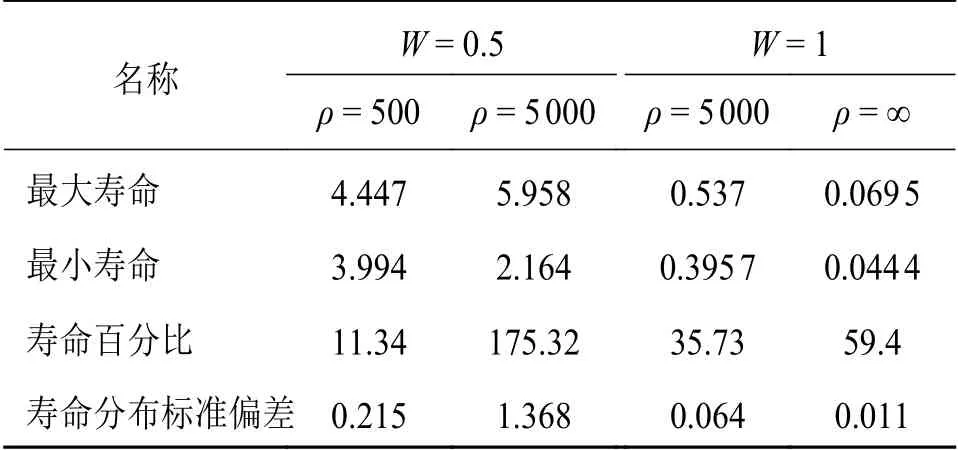
表1 分散性大小对比

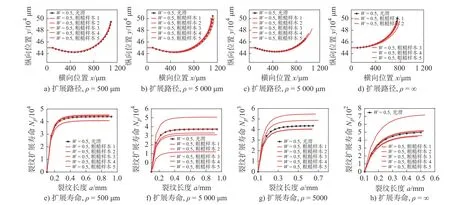
图11 裂纹扩展分散性

图11还展示了粗糙与光滑曲面计算结果对比。不难发现，部分形貌样本裂纹扩展寿命高于了光滑曲面结果，这强调了基于裂纹扩展寿命开展形貌优化设计的可能。但遗憾的是，粗糙度形貌的随机和无序特性严重妨害了上述作用机制的探究，使得至今尚未形成相关的明确结论。从随机过程理论出发，可将大多数粗糙度形貌参数与其统计分布参数关联起来[24]，由此可进一步讨论粗糙度形貌参数对裂纹扩展的影响。理论上，对于高斯分布表面，Ra和Rq分别以0.8和1的比例系数正比于标准偏差σ，这意味着减小这些形貌参数可以减小裂纹扩展的分散性。一个类似于刚刚讨论的问题是，部分大粗糙度样本的寿命为何长于小粗糙度的样本值？这也有待深入研究以揭示其内在关联。由于相关长度决定了空间参数[25]，如RSm、RS，这些空间形貌参数与裂纹扩展亦无法呈现出简明关系，这也是当前对空间形貌参数的作用没有形成一致结论的原因之一。无论如何，增大外载有利于减小上述分散性，但裂纹扩展寿命也随之减小。分散性大小对比见表1。

3 结论

1）粗糙度形貌的随机与无序特征导致其亚表面裂纹扩展呈现分散性，且裂纹扩展路径比寿命分散性小。裂纹扩展分散性随粗糙度标准偏差增大而增大，与粗糙度相关长度无显著关联，这表明减小Ra、Rq可以减小裂纹扩展的分散程度，但无法通过简单增减粗糙度空间参数来限制其分散性。

2）曲率半径对亚表面裂纹扩展深度、广度及其分散性都有很大影响。ρ=500μm 时，粗糙度效应被曲面作用充分稀释，裂纹扩展分散性较小。随着曲率半径增大，裂纹扩展分散性呈增强趋势。对于给定粗糙度形貌，可能存在最佳曲率半径，使得裂纹扩展寿命最长。

3）增大外载可以减小裂纹扩展分散性，但同时减小了裂纹扩展寿命。