Al2O3纳米流体自激式脉动传热的热流道结构优选
袁红梅,,汪朝晖,,
(1.武汉科技大学冶金装备及其控制教育部重点实验室,武汉 430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,武汉 430081)
脉动强化传热技术是提高热交换设备中的传热速率和控制扩散设备中的传质速率的有效手段之一,其脉动流主要通过使流体产生脉动或热传递表面振动产生[1]。此强化传热技术是通过特定的几何结构或直接施加脉动激励使流场产生涡旋结构,这种“有序”的涡生长及迁移过程,破坏了流体边界层,强化了近壁面附近流场的混合程度,从而实现了提高传热性能并尽量减少流动阻力的目的[2-3]。近几年,为了进一步减小紧凑式热交换设备的结构尺寸并同时提高其传热性能,脉动强化传热技术已广泛应用于不同热流道的热性能研究中。Hoang 等[4]对V 形波纹通道中湍流和脉动进行了数值模拟,结果表明波纹通道中脉动流的传热改善效果优于稳定流动。李思文等[5]实验研究了光管内湍流脉动传热的影响因素,结果表明雷诺数、脉动振幅和脉动频率对流体脉动强化传热均有显著的影响。舒梦梅等[6]对缩放管内的脉动流传热性能进行了数值研究,结果表明脉动流的传热性能优于稳态流动,强化了11.4%左右;同时,脉动流强化传热会在一定程度上增加沿程阻力,但对综合评价指标的分析表明脉动流条件下的传热性能显著增强。陈军伟等[7]数值研究了脉动流作用下翅片散热器的散热效果,结果表明脉动流能增强翅片散热器的散热效果,且存在最佳振幅使得综合换热性能最高。徐艳英等[8]实验研究了弯尾管亥姆霍茨型无阀自激脉动燃烧器尾管的传热特性,在相同频率下,脉动流传热系数约为相同雷诺数下稳态流传热系数的2.4 ~4.6倍;在相同压力振幅下,脉动流传热系数约为相同雷诺数下稳态流传热系数的3.3 ~ 4.7倍。
使用纳米流体作为热交换系统的工作介质是被动强化传热的另一重要技术。低浓度的纳米颗粒可使工作介质的导热率在很大程度上有所提高,从而使换热局部努塞尔数显著增加[9]。近年来,随着纳米流体在紧凑式热交换器中的发展和应用,研究人员开始研究脉动纳米流体的热工水力特性。Xu 等[10]实验研究了氧化石墨烯颗粒-水纳米流体在微通道中脉动流动的传热特性,结果表明在有限的微通道散热器尺寸和低入口雷诺数下,脉动和纳米流体的的组合可以获得更高的传热效率。Rahgoshay 等[11]对恒壁温管道中脉动纳米流体进行了二维数值研究,结果表明努塞尔数随脉动频率和振幅增加而略有增加,但热传递速率随雷诺数和纳米颗粒体积分数的增加而显著增大。Li等[12]数值研究了矩形波和三角波对Al2O3纳米流体的周期性脉动缝隙射流的传热和流动结构的影响,结果表明纳米颗粒体积分数和雷诺数在传热性能上表现出良好的相互促进关系,脉动频率在一定程度上的加大将更有利于改善局部和平均传热,但降低了冲击表面的温度均匀性。Sivasankaran 等[13]对多孔介质螺旋微通道散热器内脉动水基Al2O3纳米流体的热工水力特性进行了数值研究,与稳定流动条件相比,正弦速度入口条件下多孔介质微通道散热器具有更好的强化传热效果。Khosravi-Bizhaem 等[14]对螺旋盘管中的脉动强化传热进行了实验研究,脉动流动的压降比稳态流动的压降增加近3%~7%,但对流换热增量多达39%。文献[15]指出,在脉动热管中使用氧化石墨烯/水纳米流体可以将热阻降低42%左右。
目前已有的脉动激励方式主要包括自激式脉动激励和强制脉动激励。强制脉动激励大多采用脉动热管或直接施加脉动激励装置,因此需要额外的功率损耗。而自激式脉动激励则大多采用流道本身特殊的结构来获得脉动流,故而减小了能源损耗。为了在热交换设备中实现更高效、更节能的换热工艺,创新性地提出了纳米流体自激振荡无源脉动强化传热机制,并采用正交数值试验方法对自激振荡热流道的主要结构参数进行优化研究,以获得具有最佳传热性能的最优热流道结构参数配比。最终的研究结果将为紧凑式热交换设备的优化设计工作提供一定的理论基础。
1 热流道结构及其强化传热原理
自激振荡热流道结构示意图如图1所示,主要由上游流道、自激振荡腔和下游流道这3部分组成。热流道工作时,由于自激振荡腔的特殊结构,使得下游流道近壁面附近形成逆流涡,增强了近壁面附近逆流扰动效应。

图1自激振荡热流道结构示意图
图2 为自激振荡热流道涡流分布示意图,其强化传热原理为:均匀分布的Al2O3/水两相混合介质由上游流道轴向进入自激振荡腔内部,在脉动剪切层的作用下形成剪切层涡流。剪切层涡流在碰撞尖角处发生碰撞分离后,一部分剪切流形成分离涡,并沿碰撞壁流入腔室,在腔内聚结形成较大的旋转流场,同时在腔室尖角处形成较小的次生涡流;另一部分剪切流沿下游流道管壁流动,与中心主流区流体存在较大的速度差,主流区轴向速度逐渐转变为径向速度,从而形成逆流涡。腔内旋转涡流的聚结将显著影响剪切层流的流动及下游流道逆流涡的形成速度,而下游流道近壁面处逆流涡增加了近壁面附近的逆流扰动,随着逆流涡向下游迁移,于是便实现了脉动强化传热。
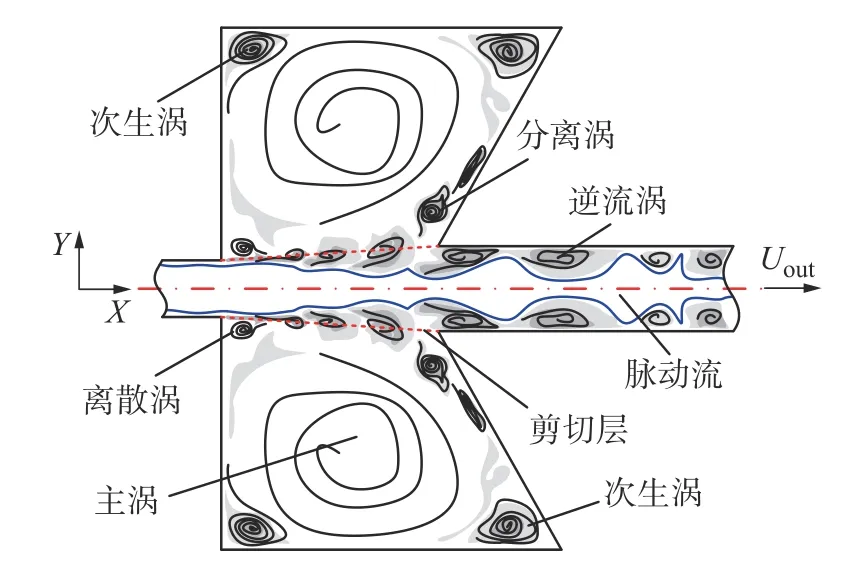
图2 自激振荡热流道涡流分布示意图
在Liu 等[16]和王乐勤等[17]的研究基础上,设计了自激振荡热流道的主要结构参数,其初始参数尺寸如表1所示。由于腔室直径D、腔室长度L和下游流道直径d2对流场中的涡流形成影响较大,故热流道结构参数的优化研究主要是围绕这3个结构参数进行的。

表1 自激振荡热流道初始结构参数
2 仿真模型的建立
2.1 数值模型
采用单相法对Al2O3纳米流体进行数值研究,纳米流体的密度ρnf、定压比热容Cpnf、粘度μnf和导热率knf的表达式[18]分别为:
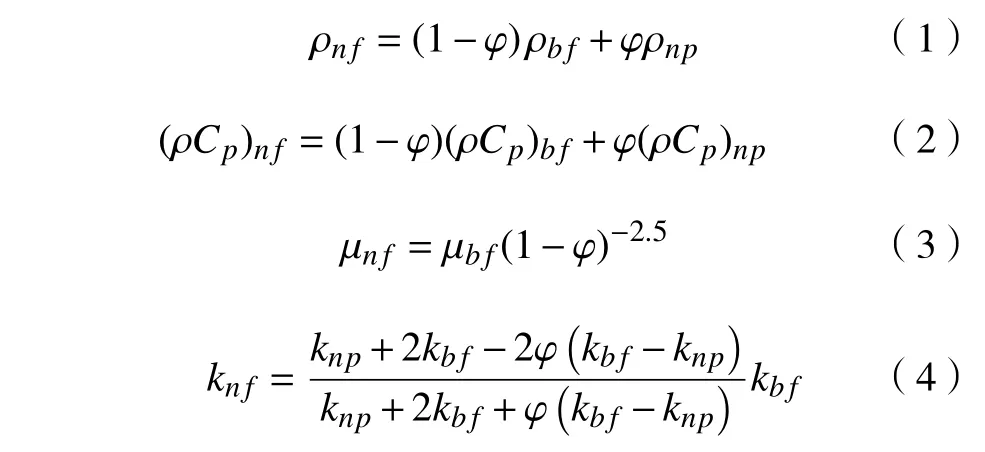
纯水和Al2O3纳米颗粒的热物理性质见表2。

表2 Al2O3纳米颗粒和水的热物理性质
湍流模型选用基于自相似理论的大涡模拟(LES)模型,该模型首先利用滤波函数过滤掉小尺度脉动,然后对大尺度脉动进行直接数值模拟。对于不可压缩流动,过滤后的连续性方程、动量方程和能量方程分别表达为:

流体流动的传热性能可用平均努塞尔数来表征,平均努塞尔数被定义为[19]
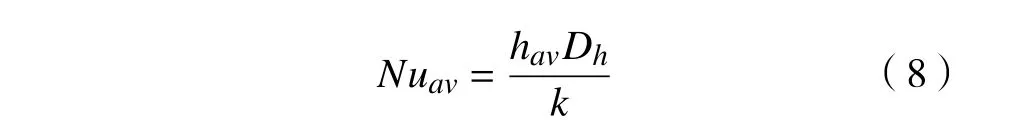
式中:k 为热导率;Dh为水力直径;hav为平均传热系数。
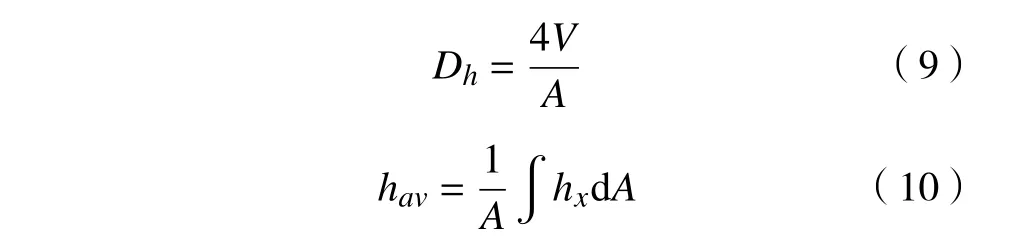
2.2 数值计算方法及边界条件
采用ANSYSFluent 19.0软件进行数值模拟,入口设置为速度入口边界条件,其入口速度大小由雷诺数(Rein= 40 000)给出,入口纳米流体温度Tin=293.15 K,出口设置为压力值为零的出口边界条件。湍流模型采用大涡模拟模型,运用压力耦合方程的半隐式方法(SIMPLE算法),亚松弛因子保持默认设置,壁面为无滑移边界条件,壁温Twall=343.15 K。考虑到控制方程和数值计算的复杂性,动量、湍动能和湍流耗散率采用2阶迎风离散格式,收敛精度设置为10-5。
2.3 网格独立性测试
为了分析网格尺寸对数值结果误差的影响程度,以水作为工作流体,在入口雷诺数Rein= 40 000时对D/d1=10、L/d1= 4且d2/d0=0.8的自激振荡热流道进行网格无关性验证。图3比较了5种网格尺寸下腔室中心线的时均速度沿轴向位置的变化情况。由图3可知,当网格节点数增加到251680之后,沿腔室中心线的时均变化曲线较为一致,故最终采用251680个节点的网格尺寸进行数值研究,以此来基本消除网格划分所带来的数值计算误差。
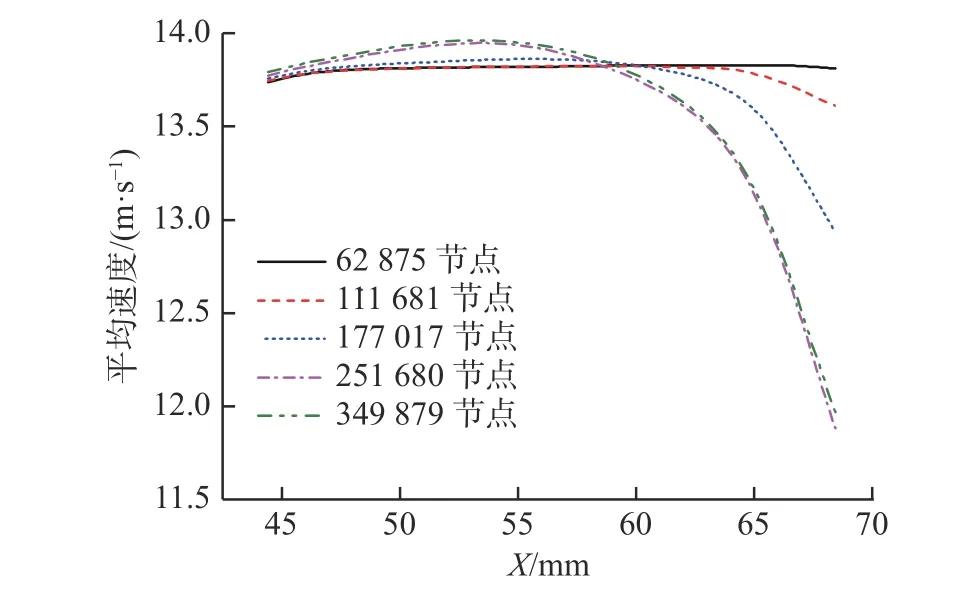
图3 不同网格尺寸下腔室中心线的时均速度
3 结构参数因素水平设计
自激振荡热流道的主要结构参数较多,本文在正交数值优化部分仅考虑腔径D、腔长L和下游流道直径d2对传热性能的影响。为了提高可视化效果,采用无量纲参数进行结果分析,具体为D/d1、L/d1和d2/d0。初步确定各因素的水平数为4,各因素的取值范围由王乐勤等[20]的研究结果获得,其中因素A(D/d1)的取值范围为10~13、因素B(L/d1)的取值范围为4 ~7、因素C(d2/d0)的取值范围为0.8 ~1.1。设计了3因素4水平的正交数值试验方案,并根据L16(45)正交试验表,确定了如表3所示的无量纲结构参数配比因素水平。
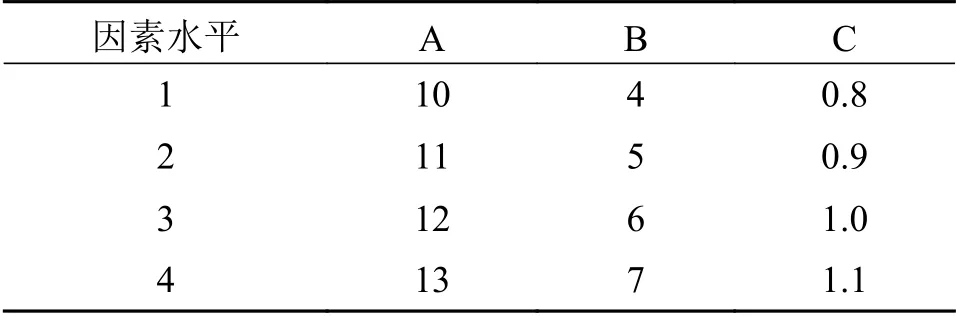
表3 热流道主要结构参数因素-水平表
4 正交数值试验结果分析
在相同工况下,根据前面所述的热流道主要结构参数,运用数值模拟方法对各结构进行了数值模拟分析,得到了16组结构下热流道的平均努塞尔数,并分别采用极差分析法和方差分析法对各因素的正交数值试验结果进行传热性能分析,以确定各因素对传热性能的影响程度。
4.1 极差分析
本次正交数值试验的16组模拟结果如表4所示,传热性能检验指标为热流道中流体的平均努塞尔数。表中k1~ k4表示不同因素水平各试验结果的平均值,R表示极差。通过分析极差的大小来判断各因素对传热性能影响的主次关系,本试验的结果显示各因素对传热性能影响从主到次的顺序为B>C>A。此外,还可根据空列来判断各因素之间的交互影响。本试验的结果显示空列对应的极差与C列对应的极差接近,故可先不考虑各因素间的交互影响。
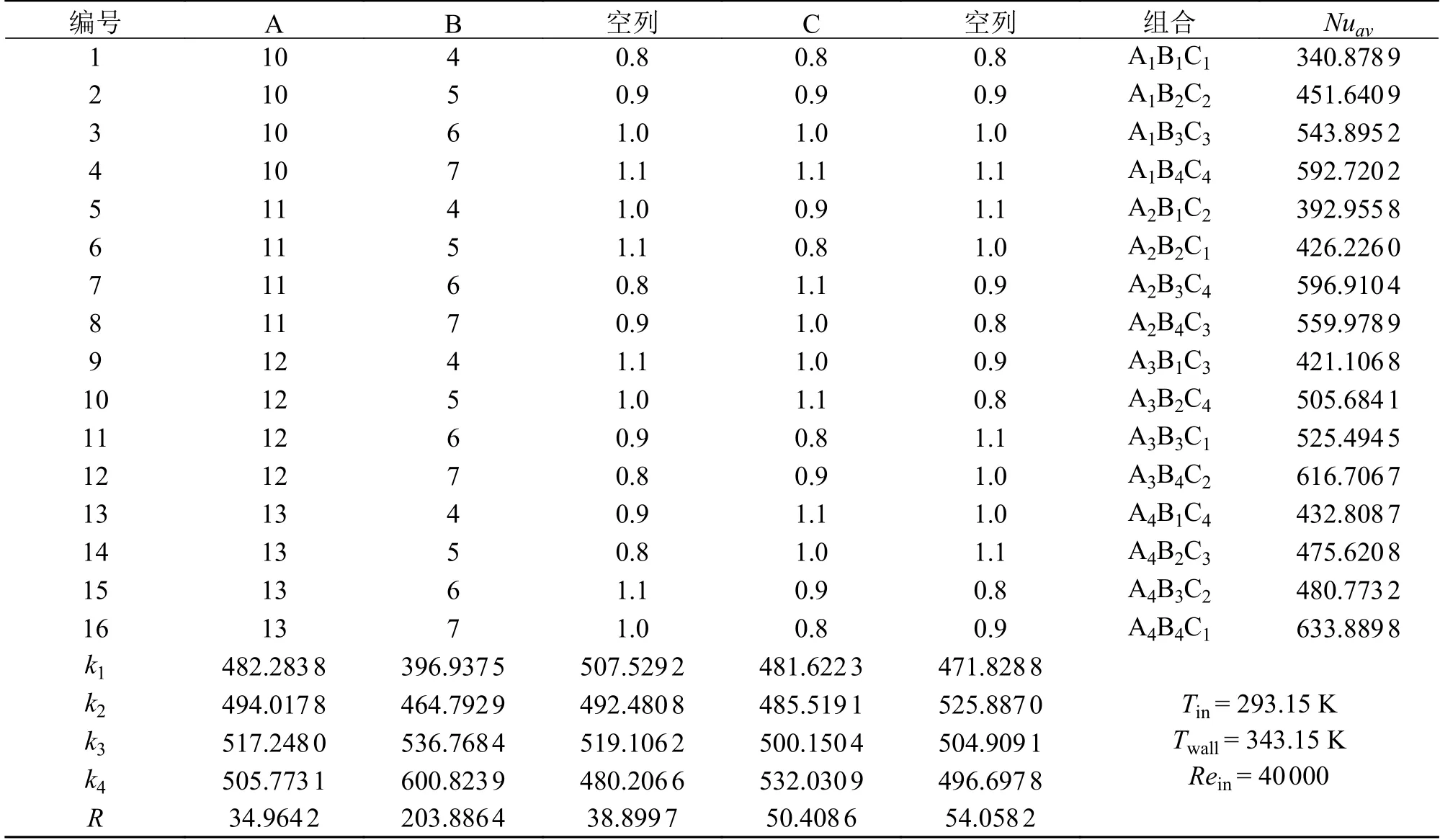
表4 正交数值试验方案及试验结果表
平均努塞尔数越大表明传热性能越好,因此对于重要因素B和居中因素C应选择k 值较大的水平,对于次要因素A 则本着降低成本原则选择适中k 值的水平数即可。综合分析表3和表4可知,本数值试验的最佳结构参数配比应为B4C4A2,即腔长L=7d1、下流道直径d2=1.1d0和腔径D =11d1。
4.2 方差分析
由于极差分析不能区分某因素的各水平所对应的试验结果间的差异是由因素水平不同所引起的,还是由试验的误差计算所引起的[21]。因此,可对正交数值试验结果进行方差分析来弥补这一不足。显著性检验可通过比较FA、FB、FC与临界值Fα的大小得出,α分别取0.05、0.01、0.1和0.2这4个水平,并通过F 分布表查得临界值为F0.05(3,6)=4.76、F0.01(3,6)=9.78、F0.1(3,6)=3.29、F0.2(3,6)=2.1。表5给出了本次正交数值试验的方差分析表,结果表明各因素对试验指标Nuav影响的主次顺序为B>C>A,方差检验结果与极差分析法一致。

表5 方差分析表
5 优化结果验证
根据正交数值试验极差分析结果可知,热流道主要结构参数的最优无量纲参数配比方案为B4C4A2。为了进一步验证该最优方案的传热性能,按照之前的数值计算方法新增一组数值试验,该最优方案定义为17#试验方案。并将17#试验方案与16#试验方案的数值分析结果进行对比,以验证最优无量纲参数配比方案的准确性。
5.1 涡量分布
涡量可以清晰地反映出纳米流体在自激振荡热流道中的流动形态,同时也间接地反映出强化传热的强弱程度。图4给出了一个脉动周期内自激振荡热流道中纳米流体的涡量分布情况。可以观察到,在t = T/4时,剪切流初步形成,此时腔室内的涡量分布集中在管壁附近,对剪切层处涡量的影响较小,便于剪切涡流的聚集和进一步沿剪切层向下游迁移;在t = T/2时,剪切流即将到达碰撞尖角,腔室入口两侧的离散涡已初步形成,并对剪切流的聚集、衍生和迁移造成一定的影响;在t =3T/4时,剪切流已在碰撞尖角处完成了碰撞分离过程,其一部分剪切流沿碰撞壁流入腔室,另一部分剪切流沿下流道管壁向下游迁移;在t =T 时,随着两部分剪切流的演变迁移,碰撞尖角处流体扰动逐渐减小,腔室入口两侧的离散涡再次生成,为剪切流形成做准备。
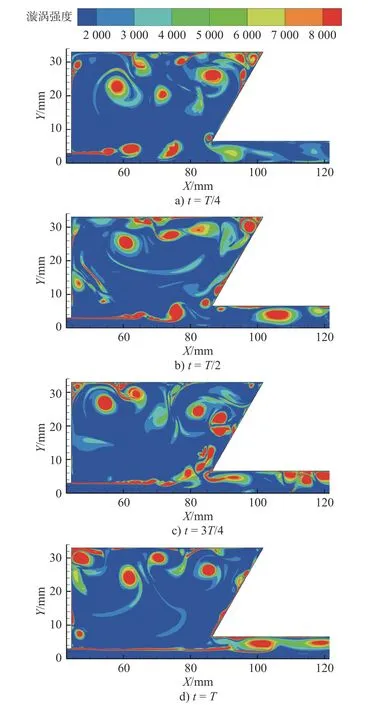
图4 一个脉动周期内热流道中的涡量分布
5.2 壁面局部温度
热流道壁面温度可以直接反映壁面与流体的热量传递程度,壁面温度越小表明热量传递越多。图5给出了自激振荡热流道的下流道壁面温度沿轴向位置的变化情况。由图5可知,新增的最优方案17#沿轴向的壁面温度明显小于方案16#,这表明最优方案的下游管道壁面与纳米流体的热量传递更多,即证实了最优方案17#更有利于增强壁面与流体之间的热量传递速率。
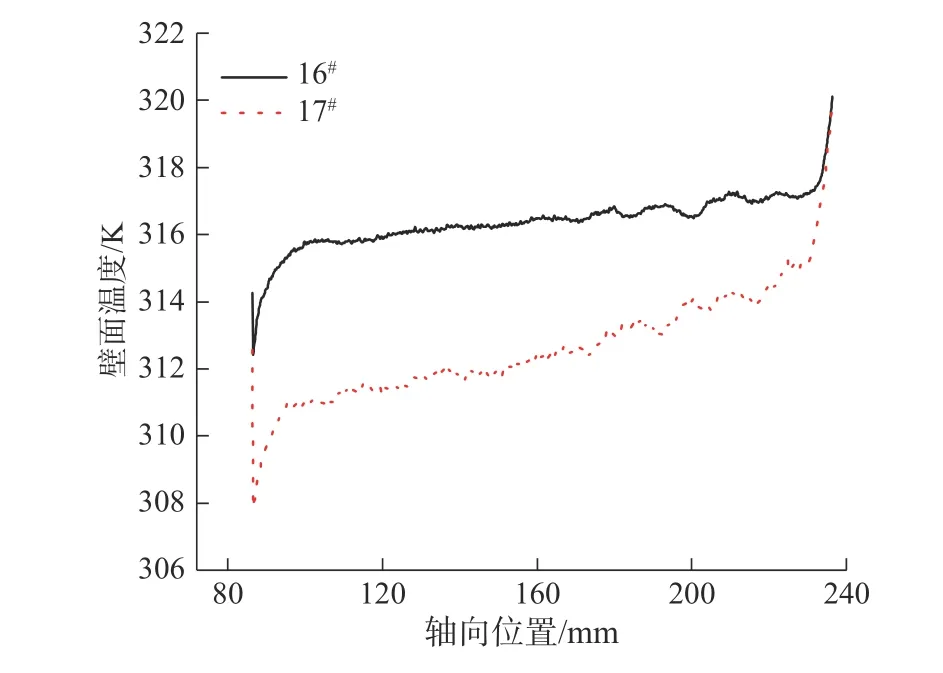
图5 壁面温度沿轴向位置的变化情况
5.3 壁面努塞尔数
壁面努塞尔数表示近壁面附近流体的无量纲温度梯度,可用来描述对流传热的强烈程度,努塞尔数越大表明越有利于增强强化传热。图6显示了下流道壁面时均局部努塞尔数沿轴向位置的变化情况,可见最优方案17#的壁面努塞尔数明显大于方案16#,这充分验证了正交数值试验所获得的最优方案的可靠性。此外,通过曲线的波动幅度可知,最优方案17#下流道中的流体扰动明显大于方案16#,说明方案17#的腔室结构能够产生较好的涡量脉动,以使得传热性能增强最佳。

图6 壁面努塞尔数沿轴向位置的变化情况
6 结论
1)采用正交数值试验方法对自激振荡热流道的主要结构参数进行优化,结果显示不同参数对热流道中纳米流体传热性能影响的显著性由高到低为腔长L>下流道直径d2>腔径D,传热性能最好的无量纲结构参数配比方案为:腔室长度L=7d1、腔室直径D=11d1、下流道直径d2= 1.1d0。
2)热流道中的涡旋结构是实现强化传热的关键,其中腔室内的涡旋结构主要是控制脉动流的形成,下流道近壁面附近的涡旋结构以逆流形式存在,主要是为了增加边界层附近的流体扰动。随着逆流涡沿下流道近壁面向下游迁移,便实现了脉动强化传热。
3)数值模拟结果显示,最优方案17#的壁面温度和壁面努塞尔数均高于方案16#,这充分说明了方案17#的自激振荡热流道具有更好的传热性能,验证了通过正交数值试验方法所获得的最优方案的合理性和可靠性。

