切削系统刀尖点动力学行为分异特征研究
马维贞,胡腾
(西南石油大学 机电工程学院,成都 610500)
切削系统(工件-刀具)在实际加工过程中发生的颤振现象是造成加工质量低、生产效率低和加工成本高等的主要因素之一[1-4]。稳定性叶瓣图表现了主轴的转速与极限切削深度的关系,加工过程中通过选择合适的转速从而避免颤振的发生[5]。切削系统的动力学参数作为稳定性叶瓣图绘制过程中的重要输入变量,会直接影响切削系统的稳定性[6]。由于陀螺力矩、离心力、轴承热预紧等高速效应的存在,在高速铣削过程中切削系统刀具的动力学行为将随着转速的变化而产生分异,从而改变整个系统切削系统的稳定性。因此,在高速铣削加工过程中,如何准确的获取切削系统中刀尖点随转速分异的动力学参数对避免颤振现象的发生具有重要的意义。
针对刀尖点动力学特性及其影响因素,国内外学者进行了较深入的研究。Iglesias 等[7]仅基于输出响应数据,对刀尖点动力学行为进行了准确的预测。Matsubara 等[8]采用冲击试验测量旋转时的频响函数,提出了一种在主轴转速变化时频响函数的预测方法。刘宇等[9]基于导纳综合法,给出了立铣加工刀尖点动态特性的预测方法;Cao 等[10]通过对高速主轴进行动力学建模,提出了一种获得与速度相关的刀尖点频率响应函数的方法。
不难看出,现阶段针对运行状态下切削系统动力学行为的研究主要借助实验检测或数字化分析。对于以实验研究为主要手段的方法[7-8]而言,避免了复杂的理论建模,但由于测试设备昂贵导致实验成本过高,并不利于企业开展现场应用;另一方面,对于以数字化分析为基础的理论研究方法[9-10],除建模过程繁复之外,在数据预处理与结果验证阶段亦需要耗费大量计算成本,且结果精确程度依赖于建模阶段对高速效应考虑的完备性与准确性;此外,部分学者在刀尖点动力学特性的研究中提出将实验与数值建模结合的半理论方法[11-12],但在刀尖点动力学参数随转速分异辨识方法的过程中,仅引入刀尖点的动力学参数,未考虑切削系统中工件动力学参数;另一方面,在辨识过程中未对模态刚度随转速的分异特征进行辨识,从而使整个切削系统中刀尖点动力学参数的辨识结果产生一定的偏差。
为此,以某立式加工中心为研究对象,以零阶频域法为切削稳定性预测理论基础,综合考虑整个切削系统的动力学特性以及运行状态下模态刚度的变化,面向切削系统提出一种基于半理论的刀尖点动力学行为随转速分异的辨识方法。该方法将分异特征辨识转化为一类优化设计问题,即以不同转速下切削系统动力学特性参数为变量,以实验标定与理论预测的极限切深及颤振频率偏差最小为目标构建优化模型,并借助粒子群退火优化算法对其进行求解,从而获取切削系统不同转速下刀尖点动力学行为的分异特征及其规律。借助所提方法能较准确地掌握切削系统动态条件下刀尖点动力学特性参数,有利于实现切削稳定性精准预测。
1 铣削系统半理论辨识方法原理
1.1 零阶频域近似的切削稳定性预测
Smith[13]提出二自由度正交切削系统极限切削深度为
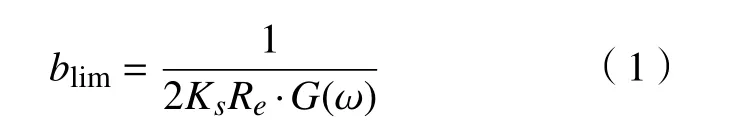
式中:Ks为切削力系数; G(ω)为切削系统的频响函数。
已有的大量半理论法对刀尖点动力学行为分异特征的研究中在建模时只考虑切削过程中刀具对稳定性的影响时, G(ω)直接被认为是刀具刀尖点的FRF[11-12]。如果考虑工件的柔性,则通过在接触点处的刀具点频域和工件频域的相加来得到系统的频域[14]

Budak 与Altintas[15]提出铣削过程中轴向极限切深和颤振频率,可由以下方式确定:

式中:N 为刀齿数;Kt为切向铣削力系数;T 为主轴周期。

式中:φex和 φst分别为切入角和切出角;Gxx和Gyy分别为切削系统(刀具-工件)在x 和y 方向刀尖点的频响函数。
则切削过程中切削系统在x 方向的频响函数为:
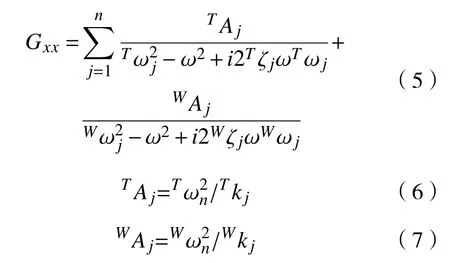
式中:Tζj为刀尖点第j 阶模态在x 方向的阻尼比;Tωj为刀尖点第j 阶模态在x 方向的固有频率;T Aj为 刀尖点第j 阶模态在x 方向的模态常数;Wζj为工件第j 阶模态在x 方向的阻尼比;Wωj为工件第j 阶模态在x 方向的固有频率;WAj为工件第j 阶模态在x 方向的模态常数; ω为激励频率。通过上述方法,可以建立刀具-工件切削系统极限切深 alim和颤振频率 ωc关 于固有频率 ωj、阻尼比 ζj和模态刚度kj的函数。
1.2 刀尖点运行动力学特性优化辨识
切削系统动力学特性共包含12 个参数,由1.1 节内容可知,极限切深与颤振频率均为切削系统非对称动力学特性参数的函数,即:

式中: alim和 ωcha分别为切削系统的极限切削深度和颤振频率;Wωx,Wωy,Wζx,Wζy,Wkx,Wky和Wky分别为工件在x 和 y向的固有频率、模态刚度和阻尼比,可由实验或者有限元分析得到Tωx,Tωy,Tζx,Tζy,Tkx和Tky为需要辨识的刀尖点在x 和y 向的动力学参数。
若结合主轴静止状态下(n=0)刀尖点动力学特性参数和工件的动力学参数,可对切削系统的极限切深alim_pre(0)与颤振频率ωcha_pre(0)进行预测,但所得结果并未计入切削系统动力学行为随转速变化的分异特征;若利用主轴运行状态下(n≠0 )刀尖点动力学特性参数和工件的动力学参数,则可预测得整个切削系统的极限切深alim_pre(n)与颤振频率ωcha_pre(n)。另一方面,通过变切深切削噪声监测实验,可对不同转速n 下实际极限切深alim_cal(n)与颤振频率ωcha_cal(n)进行标定。由于所得标定结果是不同转速下切削过程的真实反映,故其包含切削系统动力学行为分异特征。
因此,为准确辨识刀尖点动力学行为随转速变化的分异特征,需要综合考虑工件-刀具切削系统对稳定性的影响。从半理论法的思想出发,结合理论预测与实验标定结果,将不同转速下刀尖点动力学特性参数的辨识问题,转化后的优化设计问题为
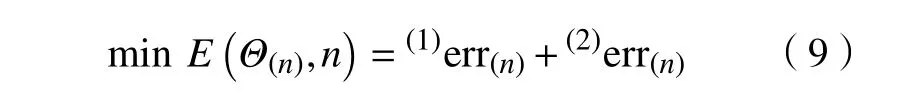
式中:(1)err(n)、(2)err(n)分别为极限切削深度、颤振频率的实验标定与理论预测结果间的相对偏差;Θ(n)为待求优化变量,即转速n 下的刀尖点动力学特性参数。

式(8)中:Tωx(0),Tωy(0),Tζx(0),Tζy(0),Tkx(0)Tky(0)分别为锤击模态实验所得刀尖点各向模态频率、模态阻尼比、模态刚度;Wωx(0),Wωy(0),Wζx(0),Wζy(0),Wkx(0)和Wky(0)分别为利用有限元分析得到的工件动力学参数。进而,利用粒子群退火优化算法求解上述优化模型[16],获取式(10)和式(11)各变量最优解,辨识得到面向主轴转速n 的铣削系统中刀尖点动力学参数。
综合1.1~1.2 节内容,可构建面向任意主轴转速的铣削系统中刀尖点动力学行为分异特征辨识方法体系,如图1 所示。
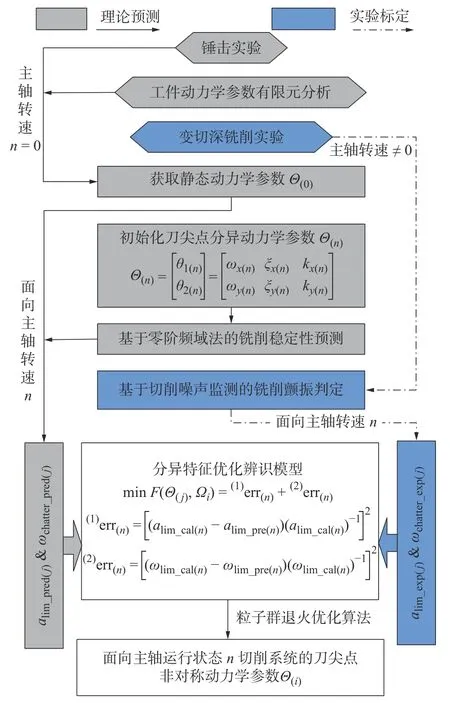
图1 刀尖点动力学行为分异特征辨识方法
2 算例与验证
2.1 工件动力学特性的有限元分析
工件长L=150 mm,宽B=107 mm 和H=60 mm。材料为AL 7075-T6,材料的杨氏模量E=71 700 MPa,泊松比μ=0.33,密度ρ=2 810 kg/m3。对工件底部进行全约束,利用有限元软件模态分析,得到工件前4 阶振型图如图2 所示。

图2 工件前4 阶模态振型图
工件在x 和y 方向前4 阶模态参数如表1 所示。
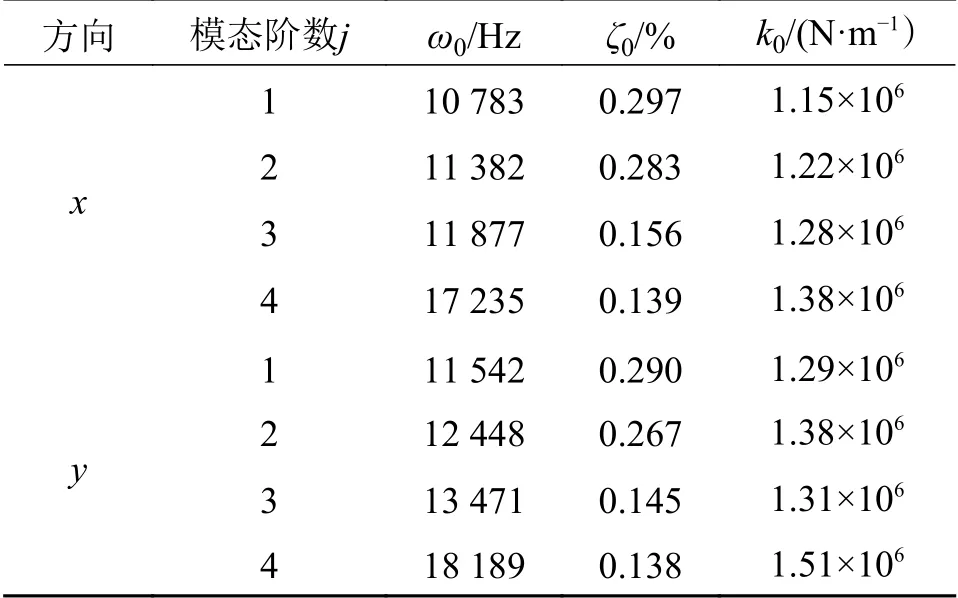
表1 工件动力学参数
2.2 立式加工中心刀尖点动力学行为分异特征辨识
2.2.1 刀尖点锤击模态实验
刀具选用硬质合金方肩铣刀,直径D=20 mm,刀齿数Z=2,实验现场如图3 所示。测得刀尖点x、y 方向前4 阶模态参数如表2 所示。

图3 锤击实验
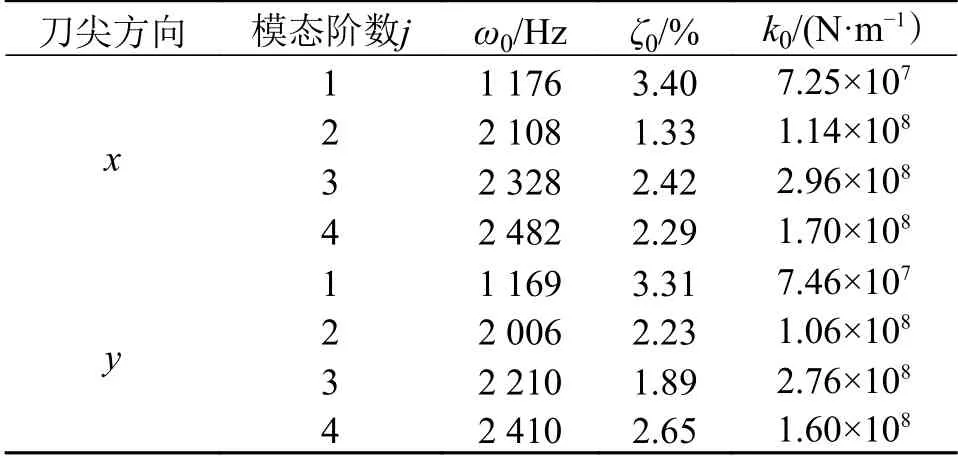
表2 刀尖点静态(n=0)动力学参数
2.2.2 基于切削噪声监测的切削稳定性标定
在VMC850 立式加工中心上搭建如图4 所示切削噪声监测实验平台,并对不同转速下变切深铣削噪声进行采集。期间,径向切宽ae(20 mm)与进给速度f 保持恒定(200 mm/min),轴向切削深度ap变化范围为[0,8] mm,进给行程120 mm,相关切削参数如表3 所示。通过分析切削噪声信号时频特征,结合工作转速、刀具齿数、锤击模态实验所得静态刀尖点动力学特性参数和通过有限元分析得到工件的模态参数等信息,可对切削系统实际切削颤振频率ωcha_cal(n)进行甄别与标定;此外,通过工件加工表面振纹出现位置的轴向深度进行测量,亦可对实际极限切削深度alim_cal(n)进行标定。

表3 变切深铣削实验参数
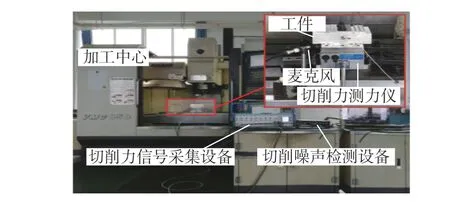
图4 基于切削噪声监测的切削颤振标定
以主轴转速n=3 000 r/min 为例,该转速下变切深铣削实验测试结果如图5 所示。由图5b)声压时域信号可知,切削噪声时域信号在28 s 左右发生突变,其幅值显著增大,说明实验过程存在不稳定切削;而从图5a)声压频域信号特征可看出,切削噪声突变部分的主频成分为1 179 Hz,该成分并非齿通基频亦或其倍频,且位于表1 中刀尖点各向1 阶模态固有频率附近;通过观测图5c)所示加工表面不难知,当轴向切深增加至5.89 mm 时,工件表面开始出现振纹,表明此时开始出现切削颤振现象。值得说明的是,随着刀具持续进给,当工件沿进给方向剩余材料尺寸小于10 mm(即刀具半径)时,径向切削宽度ae开始减小,改变了切削系统原有动力学特性,实验过程转变为稳定切削(如图5c)中颤振消除区),故振纹亦随之消失,此时轴向切深为7.32 mm。综合以上分析可知,当主轴转速n = 3 000 r/min 时,切削系统的实际轴向极限切削深度与颤振频率的标定结果分别为5.89 mm 与1 179 Hz。

图5 3 000 r/min 噪声时频信息及对应加工表面
针对转速n = 3 300 r/min,4 000 r/min 所得噪声信号及加工表面质量进行上述分析,最终可标定不同转速下实际极限切深与颤振频率,如表4所示。

表4 各转速下切削稳定性标定值
2.2.3 刀尖点动力学行为分异特征辨识
利用第1.2 节所提出的方法,辨识得到切削系统在不同转速下的模态参数,x 方向模态参数如表5所示,y 方向模态参数如表6 所示。

表5 辨识得到不同转速下x 方向模态参数
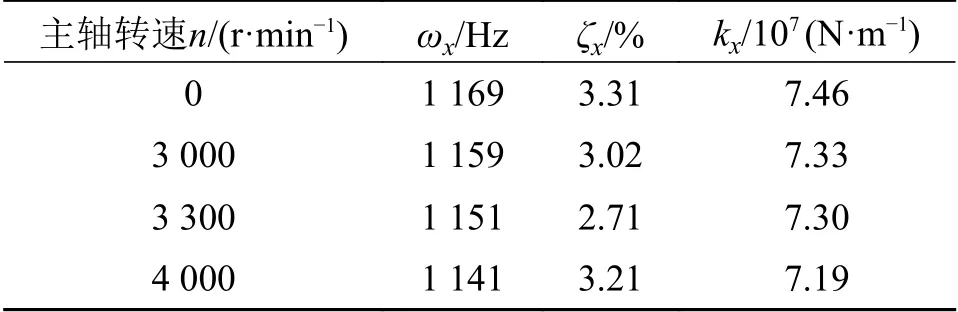
表6 辨识得到不同转速下y 方向模态参数
各参数随转速分异规律如图6 所示。由图6a)及图6b)可看出,刀尖点各向模态固有频率与模态刚度均呈现随转速增大而减小的分异规律,且转速越高,分异特征越显著;图6c)中,刀尖点各向模态阻尼比亦随转速变化而产生分异,但未见较明显分异规律。

图6 模态参数随转速分异规律
3 结果讨论与验证
利用表5 和表6 辨识所得刀尖点分异动力学参数并结合表1,对切削系统进行切削稳定性预测,可得各转速下稳定性叶瓣图,并在分析转速Ω = 3 000 r/min、Ω = 3 300 r/min 及Ω = 4 000 r/min 处做辅助垂线,得到0 转速下未考虑分异特征和3 个不同转速下考虑分异特征时切削系统各转速的极限切削深度,如图7 所示。

图7 考虑不同分异特征下极限切深预测
实验标定值、未考虑分异特性极限切深的预测值和不同转速考虑分异特性的极限切深预测值如表7 所示。其中,alim_pre(0)、alim_pre(n)分别为未考虑分异特征与考虑转速n 分异特征的极限切深预测结果;alim_cal(n)则为实验标定所得各转速下实际极限切深。根据表7 中各预测结果与标定数据间的相对误差不难看出,未考虑分异特征的刀尖点动力学特性参数并不适用于精准预测切削稳定性。利用所提方法辨识得到不同转速下动力学参数预测的极限切深与该转速下实验标定值的相对误差最大为2.7%,最小为0.33%。如图7 所示,以转速n=3 000 r/min 为例,极限切深的实验标定值为5.89 mm,但基于静态刀尖点动力学特性参数所预测的极限切深却达到了6.98 mm,相对误差为16.9%;而利用该转速下分异动力学参数Θ(3 000)可预测得极限切深为5.73 mm,与标定值相比相对误差仅为2.7%,说明所提辨识方法能较准确地获取运行状态下切削系统的刀尖点动力学行为分异特征,并能最终借以实现测切削稳定性的精准预测。

表7 未考虑分异特征与考虑转速n 分异特征的极限切深预测结果
已有研究在预测分析时,鲜有考虑刚度随转速的分异特征[8-9]。分析表5 和表6 可以发现,运行状态下切削系统的刀尖点刚度的分异是不可忽略的,刀尖点的模态刚度随着转速的升高而减小,且刚度会直接影响叶瓣图的临界切削深度[14]。因此,对刚度的辨识非常有必要。如图8 所示,以4 000 r/min为例,借助n = 4 000 r/min 的动力学参数,在考虑刚度分异的前提下,预测分析得到n = 4 000 r/min 的极限切深为6.035 mm,相对误差为0.58%。相比于未考虑刚度分异时的预测结果6.27 mm,相对误差为4.5%而言,预测精度有明显提升。所以,充分说明了辨识过程中对刚度辨识的必要性。
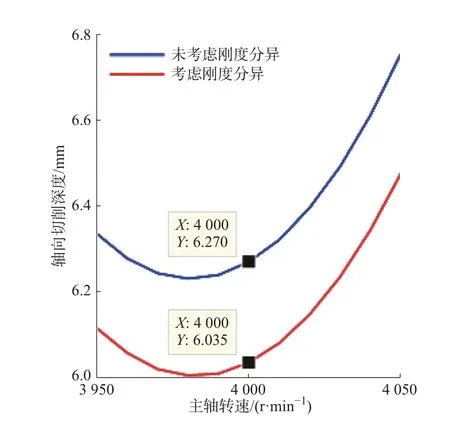
图8 刀尖点模态刚度对铣削稳定性的影响
4 结论
1) 面向主轴运行状态提出了一种基于半理论的刀尖点动力学行为分异特征的辨识与分析方法。该方法能够准确获取机床运行状态下刀尖点的动力学特性及其分异规律,并借以精准预测切削稳定性。
2) 对比分析了辨识所得各转速下的刀尖点动力学参数,结果表明刀尖点各向模态固有频率与模态刚度呈现相似分异特征,即随着转速的升高而降低;而刀尖点各向模态阻尼分异特征则表现出较强的非线性与不确定性。
3) 借助变切深铣削实验验证了刀尖点模态刚度分异特征对稳定性的影响规律,数据对比分析表明,充分考虑刀尖点模态刚度分异特征有利于提升铣削稳定性预测精度。

