一类扰动线性方程组的迭代学习控制求解方法
李钧涛,梁聪,汤永
(1.河南师范大学 数学与信息科学学院,河南 新乡 453007;2.新乡航空工业(集团)有限公司,河南 新乡 453003)
线性方程组已广泛应用于计算机科学、工程科学等诸多领域[1-2].许多科学领域中的难题,比如分数阶积分微分方程的求解,机器人的控制方案设计等均能简化为线性方程组的求解问题[3-4].一般而言,线性方程组的求解方法主要有直接法和迭代法.在线性方程组有解的情况下,可以通过直接法,如对线性方程组的系数矩阵进行Gauss消元或Cholesky分解等来求解[5-6].迭代法具有节省大量存储和计算资源的优点,对于大规模线性方程组,一般选择迭代法求解[7-8].
在现实科学研究中,线性方程组系数矩阵的元素是由物理测量或科学仪器收集得到的,这使得系数矩阵中可能含有一定的扰动[9].例如一些网络系统不可避免地存在网络诱导时延、数据包丢失和环境干扰等问题[10].由于扰动的不确定性,导致无法利用直接法求解系数矩阵中含有扰动的线性方程组.经典的迭代法,如Jacobi,Gauss-Seidel等方法是基于系数矩阵分裂所发展的迭代法[11].当系数矩阵中含有扰动时,通过系数矩阵分裂得到的迭代式无法进行迭代更新.文献[12-13]利用随机Kaczmarz迭代法分别给出了当线性方程组右端向量含有扰动时的迭代解与真实解的期望误差界.Kaczmarz迭代法通过利用系数矩阵的行向量进行迭代更新,其不能应用于系数矩阵中含有扰动的线性方程组的求解.
从控制理论的角度研究线性方程组求解是当前信息科学领域的一个热门研究问题.文献[14-15]利用控制理论研究数值分析中一些基本的线性及非线性迭代方法,并从控制的角度说明了如何设计求解线性或非线性方程组的标准迭代方法.文献[16]通过最优控制设计,得到了线性方程组的全局收敛算法.文献[17]引入迭代学习控制(Iterative Learning Control,ILC)的思想,通过线性离散系统的状态反馈设计出迭代更新律,并最终得到线性方程组的所有解.以上文献表明,控制设计与分析已成功运用于线性方程组的迭代求解.然而,上述方法均未考虑系数矩阵中含有扰动的线性方程组求解问题.
本文针对一类系数矩阵中含有扰动的线性方程组,通过构建确定和不确定ILC系统,将扰动线性方程组的求解问题转化为线性离散不确定系统的可镇定性问题,进而设计出迭代学习控制律,获得了扰动线性方程组的近似解.
1 问题描述
对于如下形式的线性方程组
BU=Y,
(1)
其中系数矩阵B∈Rn×m,向量U,Y分别属于Rm,Rn.本文考虑一类系数矩阵含有扰动的线性方程组
B(I+ΔB)U=Y,
(2)
其中ΔB∈Rm×m为扰动矩阵.
线性方程组(1)解的存在性可根据代数学方法来判定.在有解的情况下,可通过直接法或迭代法来获得线性方程组的解.由于系数矩阵存在扰动,上述方法难以用来探讨扰动线性方程组(2)的解的存在性及求解过程.
为了解决上述问题,构建如下不确定迭代学习控制(ILC)系统:
B(I+ΔB)Uk=Yk,
(3)
其中Uk为输入,Yk为输出.那么扰动线性方程组(2)有解等价于设计输入序列{Uk:k∈Z+},使得输出序列{Yk:k∈Z+}达到跟踪目标
(4)
令系统(3)的跟踪误差为xk=Y-Yk,输入序列与输出序列差值分别为ΔUk=-uk=Uk+1-Uk,ΔYk=Yk+1-Yk.根据文献[17],不确定ILC系统(3)达到跟踪目标(4)等价于线性不确定离散系统
xk+1=xk+B(I+ΔB)uk
(5)
是可镇定的.
本文致力于探究线性不确定离散系统(5)的可镇定性条件,获得扰动线性方程组(2)有解的判定条件,并设计迭代学习控制律来求其近似解.
2 预备知识
以下是本文推导过程中所用到的一些引理.
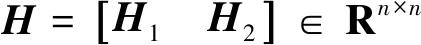
利用定义的H和F,有如下引理1和2.
引理1[17]span(B)⨁span(F2)=Rn.


注1引理2表明,对于不含扰动的线性方程组,利用确定ILC系统的学习律得到的输入序列{Uk:k∈Z+}收敛于线性方程组的解,并通过任意选取初始向量U0,得到线性方程组的所有解.
引理3[18]设A∈Rn×n是非奇异矩阵.若‖A-1‖2‖D‖2<1,则A+D是非奇异矩阵.
3 主要结果
3.1 扰动线性方程组有解的判定
由于线性不确定离散系统(5)的状态矩阵是单位矩阵,所以其能控型矩阵C=[B(I+ΔB)B(I+ΔB) …B(I+ΔB)]的秩等于矩阵B(I+ΔB)的秩.当矩阵C行满秩(即rank(C)=rank(B(I+ΔB))=n)时系统(5)完全能控.接下来探讨扰动矩阵ΔB满足的条件,进而通过矩阵B的秩来判定系统(5)的能控性,即扰动方程组(2)解的存在性.
定理1若Y∈span(B),且‖ΔB‖2<1,则扰动线性方程组(2)有解.
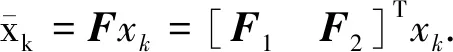
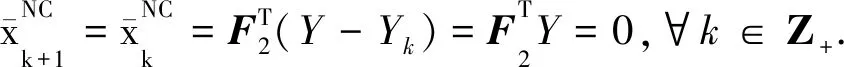
(6)
于是系统(5)可镇定,扰动线性方程组(2)有解.
注2对于一个不完全能控的线性离散系统,当其不能控部分稳定时,则该系统是可镇定的.本文中的线性不确定离散系统(5)的状态矩阵是单位矩阵,故只需让不能控部分的状态始终为0即可保证系统是稳定的.
3.2 扰动线性方程组的迭代学习控制求解
(7)

(8)
通过不含扰动的确定ILC系统(7)来研究不确定ILC系统(3).Lyapunov函数是分析系统渐近稳定的有力工具[19].当系统(8)可镇定时,通过Lyapunov函数设计迭代学习控制律,从而得到不确定ILC系统(3)的学习律.
定理2当Y∈span(B)时,状态反馈控制
确保线性离散系统(8)渐近稳定,并且迭代学习律
(9)
其中U0为任意选取的初始向量,0<γ<2是一个常数.

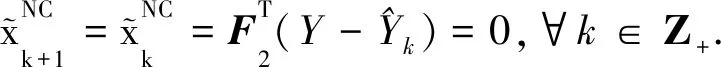
(10)

注3定理2表明,在学习律(9)下,输入序列{Uk:k∈Z+}与输出序列{Yk:k∈Z+}分别收敛于U,Y.对确定ILC系统(7)两边取极限,有BU=Y.可见U恰为线性方程组(1)的解.
针对不确定ILC系统(3),采用学习律(9),考察输出序列{Yk:k∈Z+}与扰动方程组(2)的右端向量Y之间的误差.
定理3若Y∈span(B),且‖ΔB‖2 其中U为线性方程组(1)的解. 推论1若Y∈span(B),且‖ΔB‖2足够小时,则线性方程组(1)的解U为扰动方程组(2)的近似解. 考虑如下扰动线性方程组 B(I+ΔB)U=Y, 其中ΔB是未知的扰动矩阵, 显然rank(B)=3,选择系数矩阵B的前3列构成行满秩矩阵 (11) 为了验证所提方法的有效性,在系数矩阵B中分别加入服从标准高斯分布和区间(0,1)上均匀分布的随机扰动. 例1利用MATLAB生成由标准高斯分布的随机数组成的矩阵,以其0.001的倍数作为扰动矩阵 可计算出‖ΔB1‖2=0.002 4.选择初始输入向量U0=[1 0 0 1]T,在学习律(11)下,输入序列{Uk:k∈Z+}各分量的变化曲线及输出序列{Yk:k∈Z+}与扰动线性方程组(2)右端向量Y之间的跟踪误差变化的仿真结果如图1和图2所示. 图1给出了在学习律(11)下输入序列Uk的各个分量随迭代次数的变化曲线.从图1中可以看出,随着迭代次数的增加,输入序列{Uk:k∈Z+}收敛于U1=[1.75 0.25 -0.75 -0.25]T,而U1恰为线性方程组BU=Y的解.图2给出了不确定ILC系统(3)的跟踪误差‖Y-Yk‖随迭代次数的变化曲线.从中可以看出,经过多次迭代后,其跟踪误差逐渐减小,且第15次的迭代输出为 Y15=[0.998 4 2.000 2 3.000 2 -0.001 4 1.996 8 2.995 2]T. 此时不确定ILC系统(3)的跟踪误差为‖Y-Y15‖2=0.006 1,小于定理2所提的误差界,即‖Y-Y15‖2=0.006 1<‖ΔB1‖2‖B‖2‖U1‖2=0.030 2. 例2利用Matlab生成由区间(0,1)上均匀分布的随机数组成的矩阵,以其0.001的倍数作为扰动矩阵 可计算出‖ΔB2‖2=0.001 7.选择初始输入向量U0=[1 0 1 0]T,在学习律(11)下,输入序列{Uk:k∈Z+}各分量的变化曲线及输出序列{Yk:k∈Z+}与扰动线性方程组(2)右端向量Y之间的跟踪误差变化的仿真结果如图3和图4所示. 从图3中可以看出,随着迭代次数的增加,输入序列{Uk:k∈Z+}收敛于U2=[1.25 0.75 -0.25 -0.75]T,而U2也为线性方程组BU=Y的一个解.从图4中可以看出,经过多次迭代后,其跟踪误差也逐渐减小,并且第18次的迭代输出为 Y18=[0.998 4 2.000 2 3.000 2 -0.001 4 1.996 8 2.995 2]T. 此时不确定ILC系统(3)的跟踪误差为‖Y-Y18‖2=0.005 3,仍然小于定理2所提的误差界,即‖Y-Y18‖2=0.005 3<‖ΔB2‖2‖B‖2‖U2‖2=0.017 7. 本文基于迭代学习控制的思想,探讨了一类扰动线性方程组解的存在性判定条件,并给出了其迭代求解算法.利用系数矩阵的列向量与常数项的关系以及扰动矩阵的上界,给出了扰动线性方程组有解的充分条件.设计迭代学习控制律,获得不确定ILC系统跟踪误差的上界及扰动线性方程组的近似解.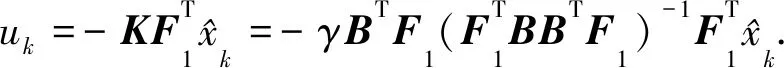

4 仿真算例
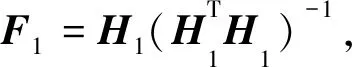


5 结 论

