二维随机变量独立性分析及教学案例设计

贺方超，陈金玉，汪 慧

（湖北工业大学理学院 湖北 武汉430068）

随机变量独立性问题是概率论与数理统计课程中的重难点内容。求解二维离散性随机变量的独立性问题，通常做法是基于独立性的定义，利用充要条件，求出其分布函数或边缘分布律。这种解题思路有时计算比较复杂，而且思考具有一定的局限性。所以，为培养学生的开放性思维和创新能力，本文主要运用联合分布矩阵推导了在二维随机变量相互独立的条件下较为简明直观的定理，并将它们应用到实例求解中，简化了计算过程，起到了 “四两拨千斤” 的作用。

1 预备知识

性质1[1]设（X,Y）是二维随机变量X,Y，随机变量相互独立的充要条件是：对任意的实数x,y，二元函数

其中F x,y，为（X,Y）的联合分布函数，FX x和FY y分别为X和Y的边缘分布函数。

性质2[1]二维离散型随机变量X,Y相互独立的充要条件是：对任意的i,j=1,2…,，都有pij=Pi.P.j。其中，pij为（X,Y）的联合分布律，Pi.和P.j分别为X和Y的边缘分布律。

性质3[1]二维连续型随机变量X,Y相互独立的充要条件是：对任意的实数x,y，有

几乎处处成立。其中，f x,y为（X,Y）的联合概率密度函数，fX x和fY y分别为X和Y的边缘概率密度函数。

2 发现问题

在讲解《概率论与数理统计教程》第三章第四节随机变量的独立性时[1]，常常会给学生补充如下类似的题目作为随堂练习。

课堂例题 已知二维离散型随机变量（X,Y）的联合分布律如表1（p137）所示，其中随机变量X和Y相互独立，试求表中常数a，b，c的值。

表1 课堂例题中的二维离散型随机变量分布律

解：先求出X和Y的边缘分布律，

X x1 x2 Pi. a+1 9+c b+4 9 Y y1 y2 y3 P.j a+1 9 b+1 9 c+1 9

由于X和Y相互独立，根据离散型随机变量独立性的性质2可列出等式：

观察与思考：根据上述求得的数值，我们不难观察到一些很有意思的情形：

这些有意思的比式能够成立是偶然的还是必然的？因而，我们猜想在相互独立的情形下，二维离散型随机变量是否普遍存在着这样的规律？如果有的话，我们是否可以通过验证和推导获得更多更好的结论？这些问题值得去探索。基于这种想法的探讨和研究，下面我们引入分析所得的结论。

3 主要结果

首先，我们定义矩阵[2]

证明：由于 和 相互独立，根据性质2可将中任意两个非零行向量整理为

因此，矩阵 中任意非零行向量的各分量之比都相等。同理，可证列向量也具有相同的性质。

根据上述两个定理可知，增广分布律矩阵的任意两行(或两列)向量分量之比都对应相等[3]。

下面我们尝试将二维随机变量独立性推广到连续型的情形，以期得到更好的性质定理。

定理3[2]设二维随机变量的联合概率密度函数为连续函数相互独立的充要条件为：

4 应用举例

下面就基于前述随机变量独立性的性质定理，对工科概率统计课程的教学例题设计做出一些探讨[4]。

例1每个参加射击比赛的代表队由两名队员组成，每人一发子弹，以环数总和的多少来排定名次。某代表队由甲乙两名队员组成，根据历史比赛成绩，两人射击的环数能够稳定在8环、9环和10环。设X，Y分别表示甲乙两位运动员可能环数，已知X与Y的分布律如下表（表2,3）所示，且两人射击互不影响。求在这次比赛中，该代表队最有可能取得多少环的成绩？概率为多少？

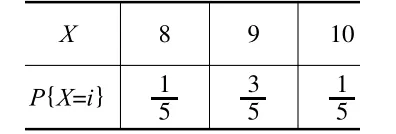
表2 甲的射击成绩

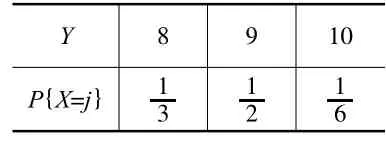
表3 乙的射击成绩

解：根据独立的离散型随机变量性质2，可构造X,Y的联合分布律如下表：

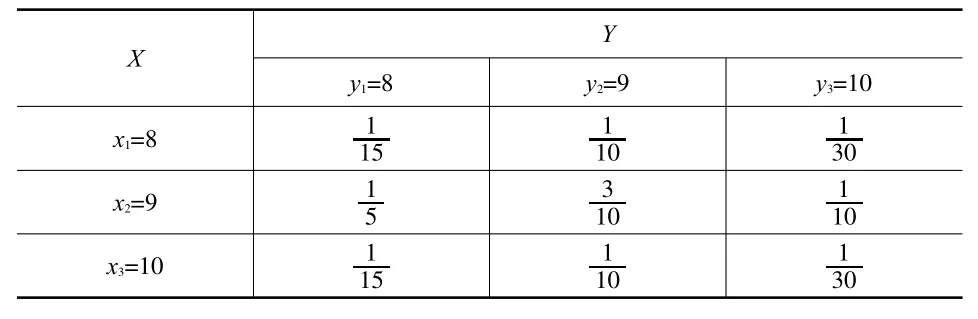
X y1=8 y2=9 y3=10 x1=8 1 15 1 10 1 30 x3=10 1 15 1 10 1 30 Y x2=9 1 5 3 10 1 10

Z P{Z=k}16 17 18 19 20 1 15 3 10 25 15 1 30

例2豌豆是一种自花传粉，闭花授粉的植物，因而其具有稳定的性状。据了解，豌豆的皱粒和圆粒外形是相对性状，豌豆的红、紫和白三种花色也互为相对性状，外形和花色两种性状相互独立。现有若干自然生长的某种外形和花色性状均相同的豌豆，这些豌豆杂交出的子一代中出现了红花皱粒豌豆，紫花皱粒豌豆，白花皱粒豌豆，红花圆粒豌豆，紫花圆粒豌豆，白花圆粒豌豆六种情形。由于部分豌豆苗出现了枯萎死亡，现在只统计出子代中皱粒豌豆占总数的圆粒豌豆占白花圆粒豌豆占红花圆粒豌豆占请预测子代中其他四种性状的占比。

解：设变量X与Y相互独立，皱粒，圆粒，红花，紫花，白花，六种表现性状的分布律如下表：

X y1 y2 pi.x1 Y x2 y3 a b c 2 3 1 18 d 1 9 13

例3二维离散型随机变量（X,Y）联合分布律的部分数值如下表所示（表4），假定随机变量X和Y相互独立，求表中其余未知的概率值。

表4 二维离散型随机变量X和Y联合分布律

5 结语

二维随机变量的独立性问题是一个值得研究的重要方向。在遇到有关独立性的问题时，不论问题是否简单都应该认真对待，善于在解决问题过程中进行整理和归纳思考，从不同角度尝试不同的解题思路，探寻更多有用的规律[5，6]。本文基于已有的二维随机变量独立性性质，从一道日常课堂例题中的有趣发现出发，追根溯源，逐步得出了二维随机变量独立性的三个重要结论，为问题的求解提供极大的方便。本文最后一部分列举了一些实际生活中二维随机变量联合概率的应用例子，掌握本文这些定理可以方便快速地求解，同时也可以运用这些定理去研究日常生活中出现的关于二维随机变量独立性的问题[7-9]。