PSO算法在大型项目施工现场微型消防站选址中的应用

顾 涛

北京市海淀区消防救援支队，北京 100089

0 引言

大型项目施工现场可燃物多、用火用电量大、环境复杂、人员安全意识淡薄等因素叠加，发生消防安全事故概率较大，加强应急力量建设十分必要[1]。微型消防站旨在快速响应突发险情，有效控制或扑救初期火灾，以有效保障生命财产安全，对“救小救早”和遏制“小火亡人”事故发挥着重要作用[2]。

近年来，各地为提高施工现场消防安全管理水平，纷纷建设微型消防站。例如，北京市2016年在全市轨道建设施工现场和城市副中心建设现场等大型项目中推广微型消防站建设；厦门市2020年印发《全市在建高层建筑工地消防安全专项整治三年行动方案》，明确提出在建高层建筑工地要建立微型消防站。但如何科学建设微型消防站，如何优化选址设计等，各地尚无具体规范规章，且城市和建筑业的发展，也不可能直接套用固定选址原理。

有别于传统消防站，施工现场微型消防站建设需要综合评估消防风险因素，充分考虑响应时间、经济、灭火救援能力等因素，根据施工现场实际选用设计、选址方案。考虑到微型消防站选址面临多目标优化问题，本文应用多目标粒子群算法(PSO，Particle Swarm Optimization)模型，探讨大型项目施工现场微型消防站的选址。

1 基于PSO算法的微型消防站选址模型构建

PSO算法属于进化算法，通过模拟候鸟群的群聚活动行为来搜寻最佳捕食位置，具有实现容易、精度高、收敛快等优点。大型项目施工现场微型消防站选址与候鸟群觅食寻找最优路径类似，需要选出微型消防站的最佳位置。利用PSO算法在大型项目施工现场微型消防站选址模型构建中，主要考虑的因素有时效性因素、经济性因素、适应度因素、效益最大化因素等[3-4]。时效性因素要求依据火灾风险等级，设置应急响应时间；经济性因素需要考虑总费用，包括建设、维护等费用；适应度因素要求符合大型项目施工要求；效益最大化因素需要满足救灾要求，避免火灾损失。以这几点因素作为选址模型构建的优化参数，得到影响大型项目施工现场微型消防站选址的因素如表1所示[5-6]。

在微型消防站优化选址过程中，设选址模型决策变量为pij，并构建模型坐标，将施工现场坐标表示为(i,j)，有则pij=1，否则pij=0，获得目标函数约束方程式为：

st.gl(pij)≤0,l=1,2,…,s(1)

pij=[0,1]

式中，f1(pij)，f2(pij)…为R个需要优化的目标函数；gl(pij)为约束条件。

表1 影响大型项目施工现场微型消防站选址的因素

在经济指标因素优化过程中，需要充分考虑火灾损失费用、微型消防站建设与运行费用等因素，同时考虑消防站数量、覆盖范围等问题。因此，需要对消防站数量、年运营费、建设费、火灾损失等参数进行最小费用优化，如式(2)所示[7-8]。

式中，p为消防站；ij为位置参数；SC为一个消防站一年建设、运营总费用；f1(pij)为消防站建设总费用；α为可调参数；TLC为火灾年损失。

设消防站总数为N，f的导数为0，得到区域内最佳微型消防站选址数量计算公式为：

N=int(InTLC-SC+β)(3)

式中，β为修正的概率参数；int为取整函数。

在距离指标因素分析中，需要根据施工现场实际情况合理设置微型消防站的距离，考虑到响应时间与距离关系，在施工现场任意选择一个需求点q1，则在距离模型构建中认定该需求点在p1管辖范围内，考虑到距离将影响到响应时间，将其转化为距离模型得到距离优化表达式为：

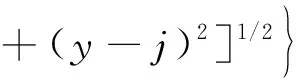
式中，(x,y)为需求点坐标；k为风险级别；p为消防站取值点。对微型消防站坐标(i,j)到事故点坐标(x,y)进行优化，得到最佳距离。

时间指标因素是指从微型消防站到达事故点的平均行车时间。设各个微型消防站消防车辆到达任意火灾点最远距离总和除以对应抵达速度总和为平均响应时间，得到响应时间的数学模型为：

式中，D为消防站p到需求点q的距离；P为消防站位置集合；Q为需求点位置集合；S为消防站响应速度。

覆盖率指标是指微型消防站能有效抵达需求点的比例，考虑到不同区域存在交叉覆盖，设指定行车时间段为[T1,T2]，则覆盖率数学模型为：

式中，qc为指定行车时间，M为需求点总数。覆盖率越大，消防车辆抵达时间越短，应急响应速度越快，且要求覆盖率达到80%才能满足应急救援要求。在实际救援过程中，理论上存在其他消防站参与救援的情况，在实际优化选址中可以考虑交叉情况，使得投入资金最优化。考虑到交叉覆盖率对整体覆盖率的影响，转化为数学问题表示为：

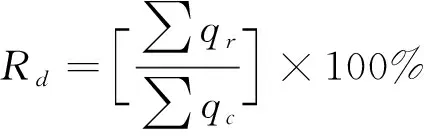
式中，qr为指定行车时间重复保护需求点个数。

针对大型项目施工现场微型消防站特点，选择Pbest策略筛选出Pareto最优解，并获得综合评价，从而完成微型消防站的选址任务。PSO算法优化选址流程如图1所示[9]。

图1 PSO算法优化选址流程图

在多目标PSO优化算法中，将根据历史个体最优解Pbest进行策略更新。在全局最优中，全局最优粒子(Gbest，Global best)将向全局最优位置靠近，选择全局最优粒子对种群Pareto起到支配效果，在算法使用需要充分考虑到Pareto支配面多样性与收敛特征，并构建外部归档策略实现全局最优解效果，Gbest策略是在决策空间中根据粒子迭代位置，得到对应相似距离为[10-11]：

式中，xi为种群第i个粒子；H为非支配解个数。

式(8)很好地反映出种群粒子与外部归档集中的粒子群最优解之间的距离关系。种群粒子与外部归档集之间的平均相似距离计算公式为：

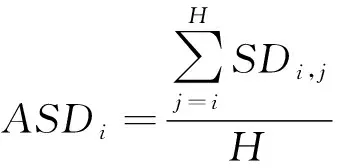
应用对比法筛选相似距离粒子值，得出外部归档集中对应的非支配解。多目标PSO算法在寻址问题中面临诸多优化问题，如算法在寻址寻优中存在局部早熟粒子收敛多样性差、收敛慢等问题，将迭代找到的Pareto非劣解引入外部归档集中，并选用线性递减策略调节惯性权重值，这种策略可以优化种群迭代前期收敛慢的问题，在后期实现大范围寻优。同时，后期为加强局部收敛效果，选择逐步减小的惯性权重值，线性递减权重更新表达式为[12]：

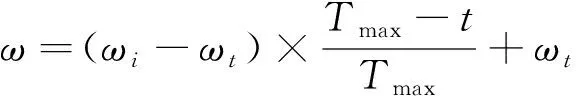
式中，ωi为终止权重；ωt为初始权重；t为迭代次数。

2 基于PSO算法的微型消防站选址模型实例应用

为检验所提出的选址模型是否满足可行性要求，以某大型项目施工现场为研究对象，进行模型实例验证。以某建设单元为例，其为框架式构造，建筑高度为32 m，楼层数为6层，总占地面积12 000 m2，总建筑面积70 000 m2，建筑内需求点情况如图2所示。选择图2中标记点为微型消防站备用选址点，采用Fine Kinney风险评估策略对项目需求点进行风险值计算。经计算得知该项目施工整体都存在较高火灾风险，选择典型的10处进行评估。模型数据测试平台为Win 10，采用Matlab 2017a软件对微型消防站选址模型进行性能测试。PSO算法在运行中设置粒子初始位置、加速常数等参数，并设迭代次数为200、随机产生的粒子数为100个。

在初始化粒子最优位置测试中，利用软件任意选择3个需求点作为微型消防站的备选地址，并将所选位置带入适应度函数，得到最终初始群适应度值。同时，在测试中将每个粒子作为个体最优，测试得到初始种群如图3所示。图3为初始化总费用种群，可见种群数量多、分布广。继续作循环迭代测试，并从集合中任意选择一粒子为总体最优粒子。通过位置、速度更新表达式得到更新的适应度取值，获得粒子种群分布图如图4所示。

图2 建筑内需求点分布图

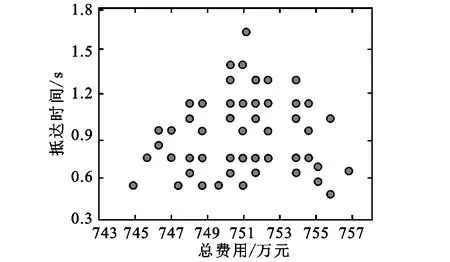
图3 初始种群

图4 第一次粒子更新后种群

经过持续迭代更新，得到较为准确的粒子群分布。对粒子设置外部归档集，对非劣解信息进行存放，初始筛选非劣解得到如图5的5个优化粒子分布图。将历史粒子集合与非劣解集进行合并，获得新集合，依据支配关系，继续筛选，经过进一步优化，得到4个最佳选址的新非劣解集如图6所示，不过筛选不够精准，需进行下一步测试。

继续对筛选出的4个最佳粒子进行优化，去掉新非劣解集重复的粒子，并再次进行迭代测试，获得如图7所示的3个最优微型消防站建设选址方案，能满足各项指标要求。在微型消防站选址中，除了考虑定量因素，还需要充分考虑时间、覆盖率、经济、距离评价指标因素，再次对3个结果进行筛选，最终得到E1为最佳微型消防站选址方案。由图7可知，E1选址点建设总价值为749万元，区域覆盖率为86%，方案满足微型消防站设计要求。

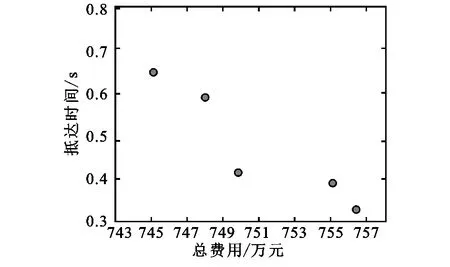
图5 初始非劣解集

图6 第一次非劣解集更新后种群

图7 最优解集分布图

3 结语

随着城市化进程加快，各类大型项目数量递增，随之而来的施工现场消防安全问题备受关注。科学布局消防站点，对消防救援力量快速到场、控制火灾蔓延，减少人员伤亡和财产损失具有重要意义[13]。本文结合大型项目施工现场特点与微型消防站设计要求，构建出基于PSO算法的微型消防站选址模型，并对选址模型展开优化，选择某大型项目为案例验证所提优化方案的可行性。测试结果表明，所提出的微型消防站选址方案覆盖率可达86%，总造价为749万元，满足设计要求。然而，本文也存在不足，如选择设计因素只有4个，尚有其他因素未充分考虑，后期可根据实际情况增加因素，使方案更全面可靠。