无人机跟踪过程中的避障问题研究
夏生吉,王道波,罗东海,姜 燕
(南京航空航天大学,江苏 南京 211106)
0 引言
因为无人机具有运行时间长、抗风险能力强和维护成本低等优点,近年来一直被广泛应用于作战、搜救及其他应用中,无人机协同跟踪目标也随之成为研究热点之一。其中,低空空域复杂多变,如何在协同跟踪过程中完成对探知障碍物的避碰,是十分重要且困难的工作[1]。
针对上述避障问题,早在1986年,Khatib[2]提出了人工势场法,引入引力场完成目标对无人机的“引力”和障碍物对无人机“斥力”的模拟,最后利用“合力”控制无人机的运动。季荣涛等[3]针对单无人机跟踪单一目标问题,先通过Lyapunov导航向量场法使无人机对目标对峙跟踪;遇到障碍时,切换为势场法控制无人机避开障碍区域。Peng等[4]结合Lyapunov向量场和避障势场函数,使得无人机在避障后实现定距跟踪。刘小伟等[5]在满足避障完成时间和无人机机动约束要求下,解算比例导引系数取值范围,通过引入比例导引将相对速度方向导引到避障方向,从而完成避障。而导引产生的路径容易发生振颤,通过模拟自然界的流水避石现象,提出干扰流体动力系统,因其能快速生成光滑路径而吸引了中外大量学者关注。Yao等[6]在IFDS中,将正切矩阵引入调制矩阵,解决流函数陷入局部极小值问题;将Lyapunov矢量场法与改进IFDS相结合,实现三维多无人机协同跟踪目标及避障。张毅等[7]基于最小侧向偏移量原则选取无人机避障策略,提出双旋Lyapunov矢量场法。在UAV动态避障过程中,将无人机与障碍的位置关系转化为相对速度关系解决飞行冲突,通常能得到不错的效果[8-9]。王宏伟等[10]提出一种调向和调速相结合的混合避障策略,在目标函数的约束下,完成最优避障策略的求解。
文献[3]、文献[6]、文献[11]和文献[12]为保证UAV在复杂情形下跟踪目标的安全,都是基于Lyapunov矢量场法,引入避障策略使得无人机有效避开障碍区域。文献[8]~文献[10]的主要研究内容是利用速度障碍法,令无人机能够在移动过程中有效地避开障碍物。在此类文献中,尚未发现将Lyapunov矢量场法与速度障碍法结合。故本文将上述2种方法结合,研究在跟踪目标条件下的避障控制方法。
1 问题分析
无人机由于具有灵活性强、快速和视觉范围广等优势,常被应用于目标跟踪任务中。对于地面目标,需要UAV持续跟踪,保证其在视野范围内[13]。本章将简化无人机运动模型,并介绍跟踪任务中主要用到的Lyapunov矢量场法。
1.1 无人机运动模型
假设无人机拥有飞行控制系统可以跟踪控制指令,故在整个跟踪任务中能够保持恒定的飞行高度,只考虑控制水平面内的空速大小和飞行航向。
基于假设,UAV在二维空间的运动模型[14]为
(1)
[x,y]为无人机在惯性坐标系下的坐标;φ为无人机航向角,φ∈(-π,π];[Wx,Wy]为无人机在x方向和y方向上受到的风扰动;[u1(t),u2(t)]为UAV线速度及角速度,其约束条件为
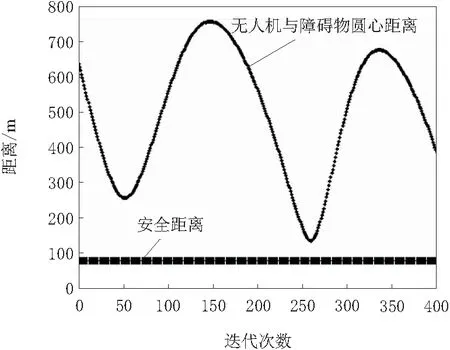
0 (2) 因为风扰动(Wx,Wy)与目标绝对速度对无人机相对速度影响是相同的,故本文假定风扰动为0。 u1控制量控制多无人机空速大小以完成协同跟踪任务,故本文认为单架无人机在跟踪过程中,始终以恒定空速v0飞行,即u1=v0。无人机跟踪目标模型如图1所示,假定目标位置和速度信息能够被无人机机载传感器捕获,无人机初始位置为[x0,y0],跟踪位于[xt,yt]的目标,对峙距离为rd,选取Lyapunov函数为: 图1 惯性坐标系下无人机跟踪目标模型 (3) 其中 (4) (5) 可通过Lyapunov矢量场函数确定无人机的应飞速度,即 (6) (7) 由式(5)进一步得到应飞航向为 (8) 对式(8)求导,可以得到 (9) 为了使无人机速度收敛到应飞速度,即φ-φd趋近于0,设计比例反馈控制律为 (10) k为比例系数。 将以障碍物中心O为圆心,ds为半径的圆定义为威胁区域。为简便运算,将无人机视为质点,无人机、威胁区域与目标点的位置关系如图2所示。本文任务是在跟踪过程中完成避障,故避障需要兼顾对目标的跟踪效果。故本文引入目标与无人机的相对位置作为参考,选取合适的避障策略,定义UT与X轴夹角为χ。 图2 单一障碍物的避碰模型 (11) 由2.1节可知,对于单一障碍物避碰,当γ<α时,无人机采取避障策略。基于单一障碍物的避碰模型,将延伸至对多障碍物的避碰问题研究。避碰主要步骤如下: a.由机载传感器获取无人机、障碍物与目标的速度、位置信息,解算出相对速度及相关角度参数。 b.选取距无人机最近的障碍物,提取该障碍物的相关参数。 c.判断γ与α的大小,若γ<α,执行d;否则,无人机依据Lyapunov矢量场法对移动目标进行跟踪。 d.判断dr是否小于r,若是则采取避碰策略;若不是,仍使用Lyapunov矢量场法。 e.判断相对速度是否解脱,若相对速度依然与落在冲突区域,依然进行避障策略;否则,继续跟踪目标,回到b。 由上述可知,针对多障碍物的避碰在步骤b时转化为对单一障碍物的避碰,故避碰策略仍是利用u2控制量改变无人机航向角,使其相对速度落在冲突区域外。u2的选取策略如下: 目标与无人机、威胁区域的相对位置决定无人机避碰时的旋转方向,即u2的正负,定义逆时针旋转时u2为正。当χ>θ时,无人机需要逆时针旋转Δγ;反之,顺时针旋转Δγ,使得无人机在避障后与目标的距离更近,有利于无人机更快地收敛和更好地观测目标。 当χ>θ时,判断θvr是否大于θ,若是,则有u2=Δγ=α-γ,否则u2=α+γ;当χ<θ时,判断θvr是否大于θ,若是,则有u2=Δγ=-(α+γ),否则u2=-(α-γ)。在式(2)约束下,无人机避碰的最大转角为±ωmax。 由于低空空域的复杂性,无人机在避障时需要面临各种情况。上述避碰算法在遇到威胁区域重叠情况时,容易造成无人机对其中一个障碍物避碰过程中,进入其他威胁区域,不能有效地避开所有障碍物。因此,利用几何关系将2个威胁区域合并,重新计算避碰算法相关参数。为简便起见,本文假设威胁区域半径相同。 如图3所示,冲突区域仍为虚线围成部分,避碰策略与2.2节一致,但避碰参数发生改变。利用2个相交威胁区域与新的障碍物区域的位置关系,可求得UO与2条正切线的夹角α。 图3 重叠障碍物合并 为了验证本文设计的算法在无人机跟踪过程中避障的效果,在MATLAB中进行仿真实验,对上述避障算法在不同条件下逐一验证。仿真中算法涉及到的主要参数如表1所示。 表1 仿真参数 无人机起始位置设置为(800,800),定义无人机航向角为速度与x轴夹角,设其初始航向角为0。目标点位置为(0,0),障碍物坐标为(200,480)。无人机利用Lyapunov矢量场法跟踪静止目标仿真结果如图4所示,不难看出威胁区域与无人机航迹重合,从而导致无人机有撞毁的危险。引入本文采取的避障策略进行MATLAB仿真,结果如图5所示。可以看出,本文提出的避障策略能够控制UAV完成避障任务,保证了跟踪任务中无人机的安全。 图4 Lyapunov法跟踪静止目标 图5 单障碍物避障仿真 由3.1节可知,本文提出的避障算法能够实现跟踪任务时对单一障碍物的避碰。为了应对跟踪任务的多样性和空域的复杂性,将在不同情况进行仿真分析。仿真参数如表2和表3所示。 表2 跟踪移动目标时障碍物参数 表3 跟踪移动目标移动障碍物参数 无人机及目标点起始位置与3.1节一致,利用避障算法进行仿真。由图6可知,无人机在完成目标跟踪任务的同时,并未进入冲突区域。图7更加直观地显示出无人机在执行任务中与障碍物中心点的距离一直保持着安全距离。利用本文提出的控制算法,无人机能够完成对峙跟踪任务,有选择性地对障碍区域1、2、3进行避碰,没有额外增加无人机飞行路径的同时,能够有效地避开威胁区域。针对移动障碍物的避碰问题,如图8所示,可以看出无人机完成了目标跟踪的要求。由图9可知,本文避障算法可以保证无人机与障碍物中心距离大于安全距离,实现了对威胁区域避碰。 图6 移动目标跟踪多障碍物避障 图7 移动目标多障碍物避障无人机与障碍物距离 图8 跟踪移动目标对移动障碍物避障 图9 移动目标移动障碍物无人机与障碍物距离 将多障碍物避障与障碍区域重叠情况融合,进行仿真实验,验证避障算法在复杂情况下的避障效果。仿真参数如表4所示。 表4 重叠障碍区域避障参数 m 仿真结果如图10所示,验证了改进后的避障算法对重叠障碍物避碰的有效性。 图10 多障碍物与威胁区域重叠避障 本文针对无人机跟踪过程中的避障问题进行建模和分析,提出将Lyapunov矢量场法和速度障碍法相结合,控制航向角变化量,引导UAV跟踪目标并避开威胁区域,确保了无人机在执行任务中的安全。仿真结果表明,该方法能够使无人机有效地执行跟踪任务,并完成对复杂空域中威胁区域的避障。1.2 Lyapunov矢量场

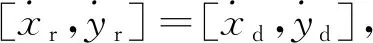

2 避障算法
2.1 避障模型建立


2.2 避碰策略与流程
2.3 重叠障碍物避碰

3 仿真分析

3.1 单障碍物避障仿真

3.2 多障碍物避障仿真





3.3 重叠障碍物避障仿真


4 结束语

