以提高最小膜厚为目标的船用水润滑轴承结构优化

吕芳蕊，夏 康，塔 娜，饶柱石

（1.河海大学机电工程学院，江苏常州 213022；2.上海交通大学机械系统与振动国家重点实验室振动、冲击、噪声研究所，上海 200240）

0 引 言

目前船舶中常采用水润滑高分子轴承作为艉轴承。与传统轴承相比，船用水润滑轴承具有显著的特点：首先，螺旋桨轴转速低，水作为润滑剂其黏度低等因素使水润滑轴承难以形成全局有效液膜，而是处于流体动压润滑与局部接触共存的混合润滑状态；其次，水润滑轴承常采用高分子材料作为衬层，其弹性变形不可忽略；再次，由于排沙和散热的需要，水润滑轴承常开有导水槽。这些特点使水润滑轴承性能与普通轴承的性能差异较大[1-4]。

已有学者分析了混合润滑、衬层弹性变形等因素对水润滑轴承性能的影响。如张胜伦等[5]考虑了瞬态冲击与弹性变形的影响，分析了高分子轴承的润滑特性及动力学特性，其研究基于全膜流体动压润滑假设，未考虑混合润滑的影响；Kraker 等[6]在Patir 和Cheng[7]提出的平均雷诺方程基础上考虑了衬层弹性变形的影响，提出了水润滑轴承的混合弹性流体动力润滑模型；作者[8]在此基础上考虑了紊流的影响，推导得到了考虑紊流的平均雷诺方程，建立了考虑紊流的混合润滑模型。由于排沙和散热需求，衬层表面常开设导水槽。Mallya等[9]研究了开有轴向槽的轴承性能，轴向槽的周向角为36°或18°，其研究结果表明，轴颈倾斜和紊流均提高了开槽轴承的承载能力；王家旭等[10-11]研究了螺旋槽及微沟槽形貌对轴承性能的影响，与直槽轴承相比，螺旋槽轴承性能有所提高，微沟槽形貌对轴承特性有一定影响。

上述研究主要建立或完善了水润滑轴承模型，为改善轴承性能，轴承设计方法的研究也得到了重视。Hirani 和Suh[12]为改善滑动轴承在稳态载荷下的性能，提出了一种通过设计轴承参数使功耗和润滑油流量具有最小值的优化设计方法；Chu[13]提出了一种利用逆方法设计滑动轴承的算法；欧阳武等[14]经分析认为增加阻尼结构后轴承动力学特性明显改善。近年来学者们发现表面织构可有效减小摩擦[15-16]，Meng 等[17-18]将该技术应用于水润滑轴承，研究了复合凹坑型表面织构对轴承摩擦学特性的影响，并得出复合凹坑可增大轴承的承载能力和减小摩擦这一结论。

上述针对滑动轴承优化的研究可在一定程度上改善轴承润滑特性，但对提高水润滑轴承的最小膜厚效果不明显。船用水润滑轴承液膜厚度极薄，甚至可能处于混合润滑状态，提高最小液膜厚度可显著降低摩擦系数、改善润滑状态、确保轴系安全可靠运行。鉴于此，本文提出一种提高最小膜厚度的轴承设计方法，即将轴承设计成端面渐扩形，也即增大轴向端面处的孔径，在此基础上针对轴颈无倾斜、轴颈倾斜两种情况分别分析端面渐扩形参数对轴承性能的影响，并提炼出可供广泛使用的端面渐扩形参数，以便工程应用。

1 含端面渐扩形结构的水润滑轴承混合润滑模型

1.1 几何模型

船用水润滑轴承由金属外壳和高分子衬层组成，由于排沙或散热需要常开导水槽（如图1（a）所示）。用作后艉轴承时，由于支撑着悬伸于船外的螺旋桨轴，轴颈易于倾斜（如图1（b）所示），轴颈与轴承孔的中心线在竖直方向产生一定夹角（以γ表示）。轴承宽度远小于轴长度，因此通常可认为γ在轴向为定值。

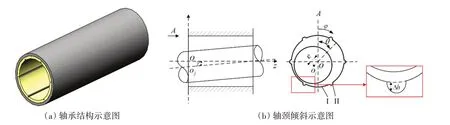
图1 船用水润滑艉轴承示意图Fig.1 Schematic diagram of a marine water-lubricated stern tube bearing

如图1（b）中A视图所示，轴颈在下沉端面的偏心距和偏位角分别以e和θ表示，则轴颈在任一轴向截面的偏心距ez可表示为

式中，z为轴向坐标。

轴颈倾角γ通常较小，因此tanγ≈γ，上式可记作

各轴向截面上轴颈的偏位角为

式中，ε为轴颈在下沉端端面的偏心率。

不考虑轴瓦变形及沟槽等影响因素时，轴承的膜厚方程为

式中，φ为从竖直方向开始计量的周向角度。

轴颈倾斜下计入衬层弹性变形与导水槽影响的膜厚方程为

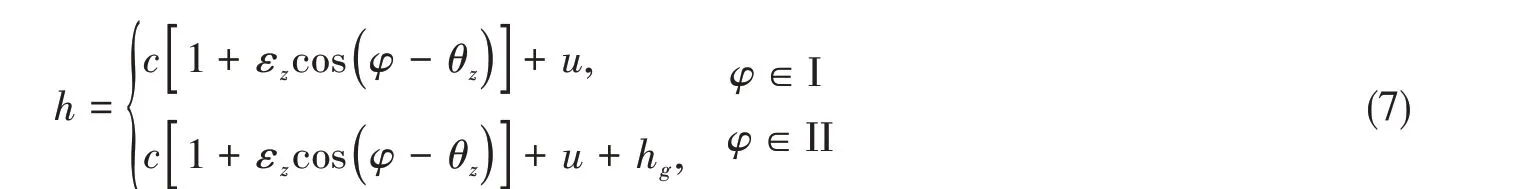
式中：I、II 分别为轴承的承载区与水槽区（详见图1（b））；hg为导水槽中节点的深度；u为衬层弹性变形，可通过式（8）求得。

式中：w为节点力；G（φj，zk，φξ，zη）为影响系数矩阵，影响系数为单位力作用在某一点（φξ，zη）引起的附近某点（φj，zk）的位移，本文通过有限元法得到。

最小膜厚是判断轴承润滑状态的关键指标，最小膜厚适当增大可减小碰摩，保障轴系正常运行。作者前述研究发现，对于轴颈无倾斜的水润滑高分子轴承，最小膜厚位于两轴向端面处，轴颈倾斜时，最小膜厚则位于轴颈下沉端。鉴于此，为改善轴承润滑特性，特别是提高最小膜厚并减小摩擦，提出在轴承轴向端面设计渐扩形结构。

将渐扩形结构的母线设计为抛物线，轴颈下沉端面附近液膜厚度变化量可记作

如图2所示，设2k1D为渐扩形结构的长度（D为轴承直径），b为轴向端面处膜厚的增大量，k2b为在渐扩形结构的轴向中分面处膜厚的增大量，0≤k1≤L/D，0≤k2≤1。由上述定义可知，k1为表征渐扩形长度的系数，k2为表征渐扩形形状的系数，b表征渐扩形深度，三参数与a1、a2、a3的关系为

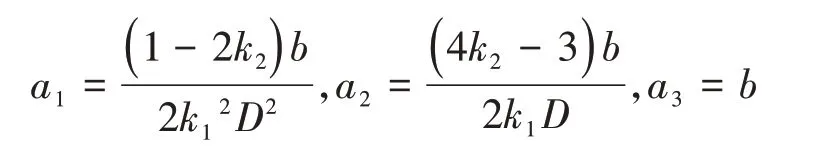
可见，渐扩形结构的形状取决于参数k1、b及k2。图2为k2取不同值时端面渐扩型轴颈无倾斜轴承的结构示意图。

图2 端面渐扩型轴承示意图Fig.2 Sketch of a bearing with gradually-expanding structures at axial ends

需要说明的是，式（10）为光滑表面假设下的膜厚方程，而船用水润滑轴承液膜极薄，表面粗糙度对轴承特性的影响不可忽略。因此式（10）中的h表示名义膜厚，即轴瓦与轴颈表面中心线间的距离，两粗糙表面间的当地液膜厚度hT为

式中，δ1、δ2分别为节点处轴颈和轴瓦粗糙表面到中心线的偏差。

1.2 混合润滑模型

稳态工况下混合润滑轴承的液膜压力可由平均雷诺方程求解得到：

式中，ϕx及ϕsx为流量因子，pˉ为液膜平均压力，h为名义膜厚，μ为润滑剂动力粘度，U为轴颈速度，hT为当地液膜厚度，σ为综合表面粗糙度。

液膜极薄时轴颈与轴承可能发生粗糙峰接触，粗糙摩擦表面建模的研究较多[19-22]，但哪个模型精确性更高尚无定论。本文利用被广泛应用的Greenwood-Tripp粗糙峰接触模型[23]计算粗糙峰接触承载力和摩擦力，粗糙峰的等效接触压力为

式中：Foilξ、Foilη分别为润滑膜动压力在水平和竖直方向的分力，A为轴承展开面的面积。

粗糙峰承载力为

式中，Faspξ、Faspη分别为粗糙峰接触力在水平和竖直方向的分力。

载荷平衡方程为

式中，W→为载荷，F→oil为润滑膜动压承载力，F→asp为粗糙峰接触承载力。润滑膜摩擦力表达式为

粗糙峰接触摩擦力表达式为

式中，fasp为两表面发生直接接触时的摩擦系数。

总摩擦力为

总摩擦系数为

2 数值求解流程及验证

利用Matlab 软件基于建立的轴承混合润滑模型编制相应的计算程序，图3 为计算流程。数值求解过程如下：给定初始偏心率及偏位角，通过方程（10）计算轴承名义液膜厚度分布，方程（10）中轴瓦变形量u在初次计算时假定为0；根据方程（12）求解液膜平均压力，并由方程（13）求解粗糙峰接触压力；根据得到的各节点压力计算轴瓦弹性变形u；将u代入方程（10）计算新的液膜厚度分布，反复迭代直至得到的压力分布满足压力收敛条件；通过方程（14）和方程（15）分别计算液膜动压力和粗糙峰接触力，直至达到载荷平衡条件。

图3 数值计算流程Fig.3 Flowchart of numerical calculation procedure

利用本文模型计算了文献[24]中的轴承，轴承参数见表1。表2 为利用本文模型所得结果与文献结果的对比，可以看到二者较为接近，因而在一定程度上验证了本文模型的正确性。值得注意的是，该算例中轴承处于流体润滑状态而未发生粗糙峰接触，并且未计入轴瓦变形等因素的影响。因而本文模型在考虑弹性变形及粗糙峰接触等多种因素影响时的正确性需通过后续实验进行验证。

表2 倾斜轴颈轴承的最大液膜压力计算结果Tab.2 Calculated maximum hydrodynamic pressures versus misalignment angles

3 轴颈无倾斜下渐扩形参数对轴承性能的影响分析

本章针对轴颈无倾斜的轴承分析渐扩形结构参数k1、b和k2对轴承特性的影响，据此选取适宜的参数，优化轴承特性。

以具有如表3所示参数的轴承为例进行分析，轴承衬层材料为赛龙，开有9个轴向导水槽，导水槽位置如图4所示。

图4 轴承开槽示意图Fig.4 Diagram of the bearing’s grooves

表3 船用水润滑轴承参数Tab.3 Parameters of the marine water-lubricated bearing

3.1 k1对轴承性能的影响

k1为表征渐扩形长度的系数，轴承直径不变时，渐扩形长度随k1的增大而增大。取四组不同的k1值分析其对轴承性能的影响，轴承1：k1=0，即无优化；轴承2：k1=0.025；轴承3：k1=0.05；轴承4：k1=0.1。在本节中，k2取定值0.25，b取定值12 μm。

图5显示的是偏心率为1.01时轴承名义液膜的厚度分布。轴承1即无优化轴承，其最小名义膜厚位于轴向两端面，这是因为两端面附近液膜压力小，由此引起的衬层弹性变形远小于内部区域。轴承的最小名义膜厚为0.5 μm，与表面粗糙度处于同一数量级，轴承中存在粗糙峰接触，处于混合润滑状态。轴承2～4的最小名义膜厚分别为8.6 μm、9.8 μm和9.2 μm，与轴承1相比均显著增大，极大地降低了粗糙峰接触发生的概率。轴承3的最小名义膜厚最大，此时k1=0.05。

图5 k1值变化时的轴承名义液膜厚度分布Fig.5 Film thickness distributions versus k1

图6为偏心率1.01下k1变化时的轴承摩擦系数及摩擦力。轴承1由于其最小名义膜厚较小，粗糙峰接触摩擦力大，因而轴承摩擦系数大；当k1增大时轴承最小名义膜厚增大，从而减少粗糙峰接触摩擦力，使摩擦系数迅速下降。而k1值取0.025 至0.1 时，轴承摩擦系数保持稳定，这是由于在该取值范围内轴承均无粗糙峰接触，在流体动压润滑状态下，最小膜厚的轻微变化对摩擦系数的影响不明显。

图6 k1值变化时的轴承摩擦力及摩擦系数Fig.6 Frictional forces and frictional coefficients versus k1

图7 为偏心率1.01 下周向角183°处液膜平均压力沿轴向分布图（最大平均液膜压力位于该周向角）。与无优化轴承（轴承1）相比，端面渐扩型轴承（轴承2、3、4）轴向两端面附近区域的平均液膜压力有所降低，且压力降低的区域随着k1的增大而增大；四个轴承的液膜压力在轴向内部区域的分布情况较为接近。

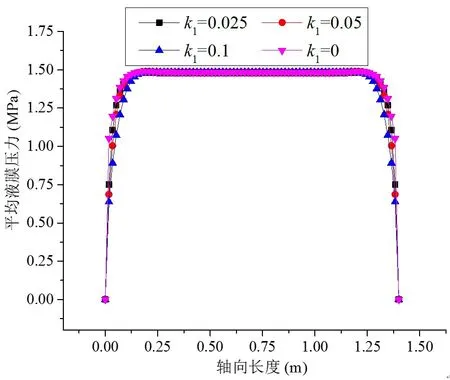
图7 液膜平均压力沿轴向分布图（周向角183°）Fig.7 Mean hydrodynamic pressure in the axial direction with a circumferential angle of 183°

图8 为不同k1及k2下轴承的最小名义液膜厚度及承载力图，偏心率为1.01。由图8（a）可见，k1=0.025 时最小名义膜厚随k2先增加后减小，这是因为当k2取较小值时，膜厚沿轴向变化较缓慢，而k1=0.025时渐扩形长度较短，在二者作用下，渐扩形对膜厚的增加作用不够明显，因此k2较小时最小名义膜厚随k2的增大而增大，当k2增大到0.5后继续增大时，渐扩形在与轴承内部的交界处膜厚增长过快，导致此处压力降低过大，进而会降低与之紧邻的轴承内部区域的弹性变形，从而导致该区域膜厚减小。当k1=0.05及k1=0.1时，最小名义膜厚随k2的增大而减小，当k1=0.05时，最小名义膜厚具有最大值。由图8（b）可见：当k1与k2增大时，承载力有减小的趋势；但当k1取0.025 或0.05 时，承载力下降幅度较小，如k1=0.05，k2=0.25时承载力仅减小1.57%。因此，为提高最小名义膜厚同时保持承载能力，选择优化参数k1=0.05。

图8 轴承最小名义膜厚及承载力随k1及k2的变化图Fig.8 Minimum nominal film thicknesses and load carrying capacities versus k1and k2

3.2 k2与b对轴承性能的影响

k2为表征渐扩形廓线形状的系数，k2＜0.5 时轴承下瓦处渐扩形为内凸，k2=0.5 时渐扩形廓线为直线，k2＞0.5 时轴承下瓦处渐扩形为内凹。分别取不同k2值对轴承性能进行计算，分析其对轴承润滑特性的影响。参数b取定值12 μm，k1取定值0.05。

图9（a）为不同k2值下名义液膜厚度沿轴向分布图（周向角为184°，最小名义膜厚位于该周向角）。由图可见，不同k2值下最小名义膜厚均位于轴向两端面。当k2=0.25 时，最小名义膜厚具有最大值；随着k2的增大，最小名义膜厚减小。当k2=0.25时，越靠近轴承端面，液膜厚度越薄；当k2为0.5及0.75时，渐扩形结构的轴向中分面处具有膜厚峰值，原因是k2较大时该位置膜厚增大；然而，此处膜厚的增大会使附近区域液膜压力降低（如图9（b）所示），进而使轴向端面处衬层弹性变形减小，最终导致轴向端面处的膜厚减小。图9（b）为不同k2值下液膜压力沿轴向分布图(周向角为183°，最大平均液膜压力位于该周向角)。由于渐扩形结构使端面附近的液膜厚度增大，因此轴向端面附近的平均液膜压力与无优化的轴承相比有所减小，并且其减小量随k2的增加而增大。

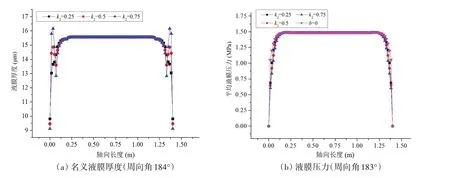
图9 名义液膜厚度及液膜压力沿轴向变化Fig.9 Film thicknesses and pressure versus axial positions

b为表征渐扩形深度的参数。图10为最小名义膜厚与承载力随b及k2的变化关系图。由图10（a）可知，b≤12 μm时，最小名义膜厚随b的增大而增大，k2取0.125时最小膜厚具有最大值；b＞12 μm时，最小膜厚先随b的增大而增大，当b继续增大时最小膜厚出现下降趋势，此时k2取0.25或0.375时最小膜厚具有最大值。当k2=0.375，b=16 μm时，轴承的最小膜厚具有最大值11.14 μm。由图10（b）可知，当b和k2增大时，承载力均有所降低，但与普通轴承相比，承载力降低幅度较小。如k2=0.375，b=16 μm 时，轴承承载力由261.7 kN 减小为255.2 kN，降低比率仅为2.37%，基本可忽略。对于该偏心率为1.01 的轴承，为提高最小液膜厚度同时保证承载能力，选取k1=0.05，b=16 μm，k2=0.375作为优化参数。

图10 偏心率1.01时轴承最小名义膜厚与承载力随b及k2变化关系图Fig.10 Minimum film thicknesses and carrying capacities versus b and k2,with an eccentricity ratio of 1.01

偏心率影响优化参数b与k2的选取。偏心率为0.99时轴承最小名义膜厚和承载力随b及k2的变化关系如图11所示，其变化趋势与偏心率1.1时（图10）接近，但轴承的最小液膜厚度的最大值出现在k2=0.375、b=8 μm 时，此时最小膜厚由无优化时的10.82 μm 增大至16.48 μm，承载力降低1.3%。由此，当该轴承偏心率为0.99 时，为增大最小液膜厚度同时保证承载力，取渐扩形结构参数k1=0.05，k2=0.375，b=8 μm。

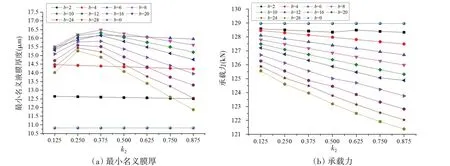
图11 偏心率0.99时轴承最小名义膜厚及承载力随b及k2变化关系图Fig.11 Minimum film thicknesses and carrying capacities versus b and k2 for an eccentricity ratio of 0.99

上述两算例中无量纲优化参数k1和k2取值相同，经典型算例验证，选取k1=0.05，k2=0.375作为渐扩形结构参数对轴颈无倾斜的普通大型水润滑艉轴承均可较显著地提高最小膜厚，而削弱承载力并不明显，参数b则需结合载荷等因素进行选取。

4 轴颈倾斜下渐扩形参数对轴承性能的影响分析

轴颈倾斜下，液膜厚度沿轴向不再均匀分布，最小膜厚出现在轴颈下沉端面，最高液膜压力靠近轴颈下沉端（如图12所示）。为提高最小液膜厚度并尽可能减小对承载力的影响，仅在轴颈下沉端设计渐扩形结构。本章根据上一章的分析，k2取为0.375，分析b与k1的取值。

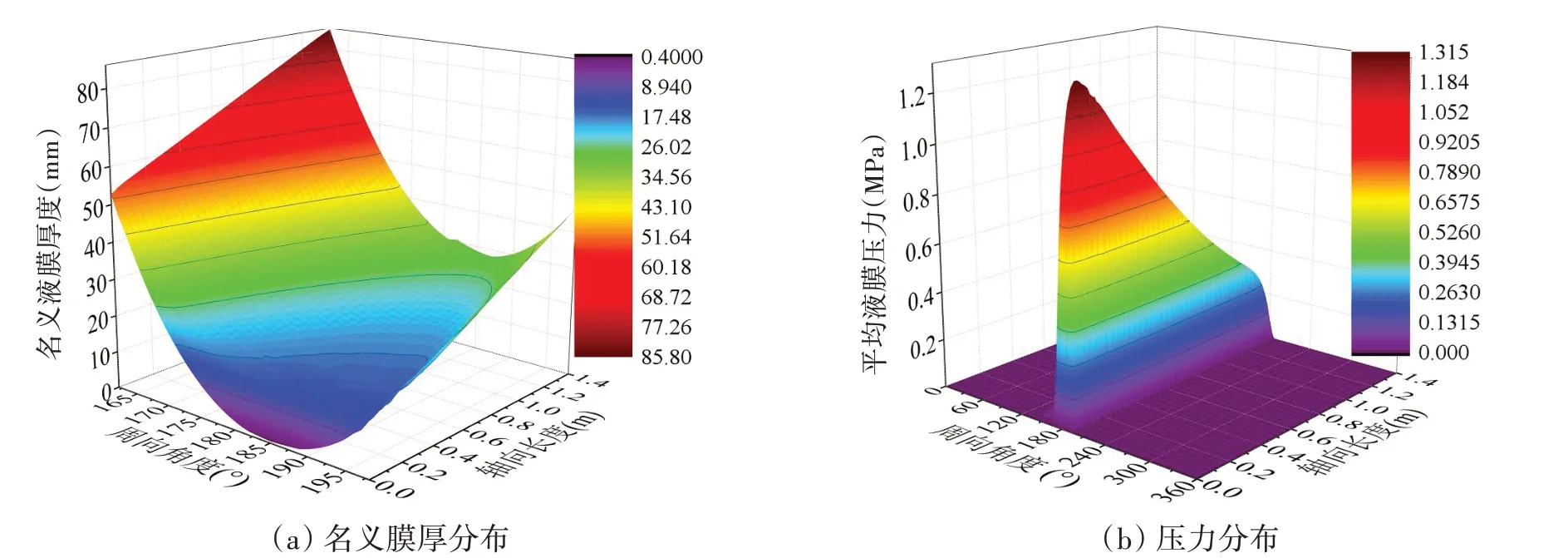
图12 轴颈倾角0.025 mrad下轴承性能Fig.12 Characteristics of the bearing for a misalignment angle of 0.025 mrad

图13（a）为不同k1下，轴颈倾斜时液膜厚度沿轴向的分布情况。k1为0.025 时，最小名义膜厚最小，且位于渐扩形结束处，这是因为渐扩形轴向长度较短，尚未覆盖无优化时最小膜厚显著下降的区域；k1取值为0.05至0.2时，膜厚分布形态不同，但最小膜厚比k1为0.025时显著增大，数值较为接近，且均出现在轴颈下沉端面。图13（b）为不同k1下轴颈倾斜时液膜压力沿轴向的分布情况。可见，渐扩形结构会降低端面处的液膜压力，随着k1的增大，最高液膜压力逐渐减小，且其位置逐渐远离轴颈下沉端面；k1由0.025 增大至0.05 时，液膜压力变化较小，k1由0.05 增大至0.2 时，轴颈下沉端附近区域液膜压力显著降低。

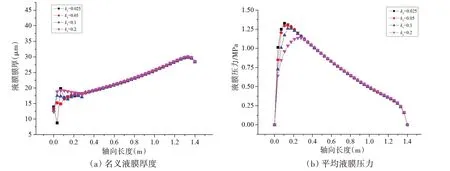
图13 轴颈倾角0.025 mrad下名义液膜厚度及液膜压力沿轴向变化Fig.13 Film thicknesses and pressure versus axial positions for a misalignment angle of 0.025 mrad

图14为b与k1对轴承最小名义膜厚及承载能力的影响图。由图14（a）可见，b值较小时，最小膜厚随b的增大显著增大，当b达到16 mm 左右并继续增大时，最小膜厚增大缓慢甚至有所下降；当k1为0.025时，b取16 mm时最小膜厚具有最大值；随着k1的增大，最小膜厚最大值所对应的b值有增大的趋势。由图14（b）可见，承载力随b及k1的增大而减小，其中k1为0.025 及0.05 时，承载力下降量在5%以内，当k1继续增大时，承载力下降显著加剧。总体而言，当k1为0.05，b为16 mm时可较明显地提高最小膜厚（由0.5 μm增大至10.5 μm），同时承载力下降量较小，因此取优化参数k1=0.05，b=16 mm。

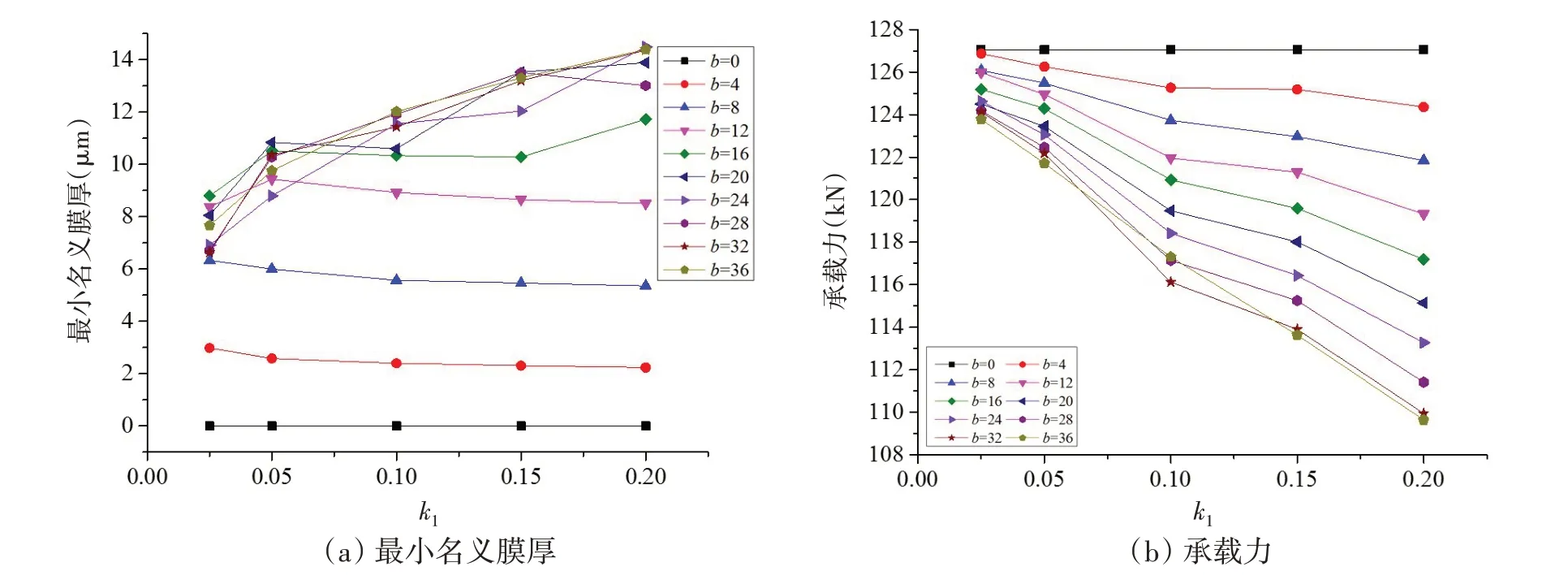
图14 不同b和k1下的轴承最小名义膜厚及承载力（轴颈倾角0.025 mrad）Fig.14 Minimum film thicknesses and carrying capacities versus b and k1 with a misalignment angle of 0.025 mrad

图15及图16分别为倾角0.05 mrad及倾角0.075 mrad下最小名义膜厚与承载力随优化参数b与k1的变化情况。可以看到，不同倾角下最小膜厚随优化参数b及k1的变化趋势较为相似。而倾角增大时随着b及k1的增大，承载力下降更加显著，这是因为倾角增大时轴颈下沉端附近承担的载荷比例增大，因此，b及k1过大易降低承载能力。为兼顾最小名义膜厚与承载能力，仍取优化参数k1=0.05，b=16 mm。

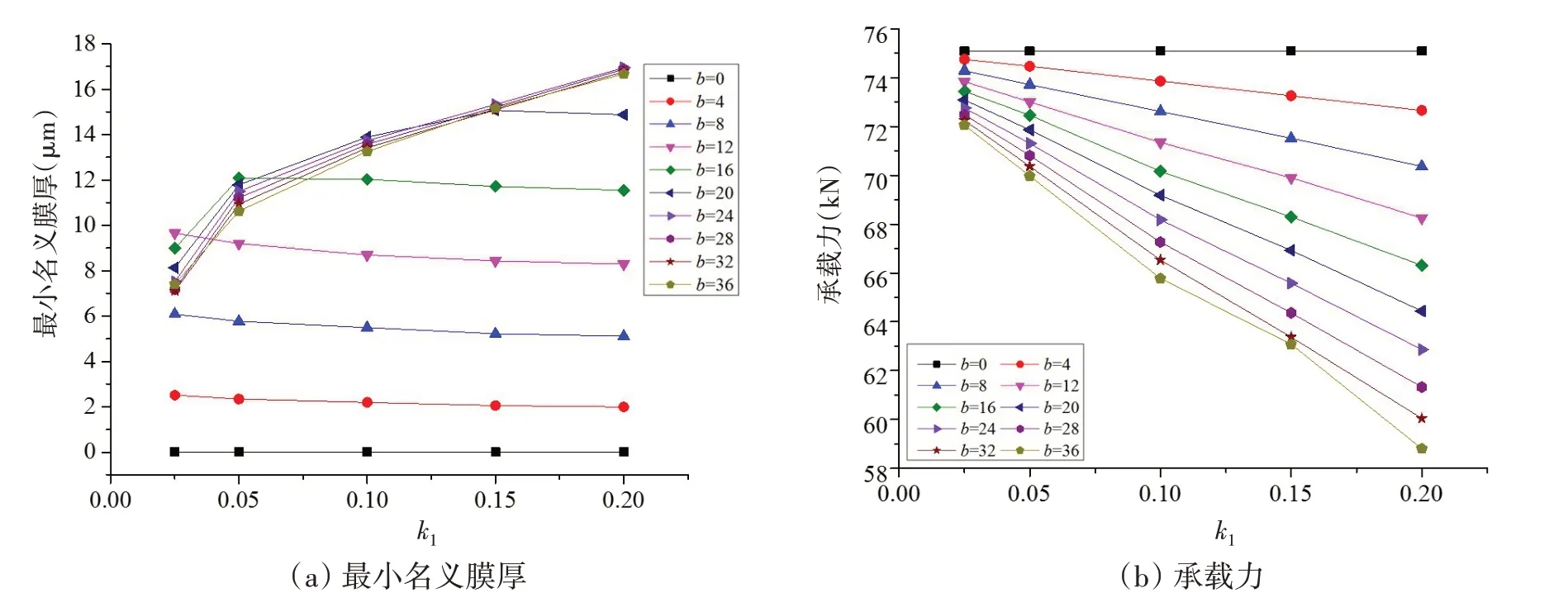
图15 不同b和k1下的轴承最小名义膜厚及承载力（轴颈倾角0.05 mrad）Fig.15 Minimum film thicknesses and carrying capacities versus b and k1 with a misalignment angle of 0.05 mrad

图16 不同b和k1下的轴承最小名义膜厚及承载力（轴颈倾角0.075 mrad）Fig.16 Minimum film thicknesses and carrying capacities versus b and k1 with a misalignment angle of 0.075 mrad

综上，该轴承轴颈倾斜时，取优化参数k1=0.05，k2=0.375，b=16 mm 可显著提高最小名义膜厚（如轴颈倾角为0.025 mrad 时，最小液膜厚度由0.5 μm 增大至10.5 μm），同时承载力的降低量较小，当倾角不超过0.075 mrad时，承载力的减小在5%以内。该优化参数与相同工况下轴颈无倾斜轴承的优化参数相同。

5 结 论

为改善船用水润滑轴承的润滑特性，特别是提高最小膜厚从而改善润滑状态以减小摩擦，提出了增大轴向端面处的孔径，即在端面设计渐扩形结构的方法，建立了相应的混合润滑分析模型及数值求解流程。分析结果表明：

（1）当无渐扩形结构时，船用水润滑轴承最小名义膜厚位于轴向端面处，端面附近区域处于混合润滑状态，轴承摩擦系数较高；当设计有端面渐扩形结构时，最小名义膜厚显著增大，轴承由混合润滑状态转变为流体润滑状态，承载能力略有降低，但降幅较小，甚至可忽略不计。

（2）对于轴颈无倾斜的船用水润滑轴承，轴向两端面均应设计渐扩形结构。渐扩形参数k1和k2为无量纲系数，取k1=0.05、k2=0.375 作为渐扩形结构参数对轴颈无倾斜的普通大型水润滑艉轴承，均可显著提高最小膜厚，同时对承载力的削弱作用不明显，参数b则需结合载荷等因素进行选取。

（3）对于后艉轴承等轴颈易于倾斜的轴承，应仅在轴颈下沉端设计渐扩形结构。随着倾角的增大，渐扩形的长度和深度增大时承载力明显下降，因此对于轴颈倾斜的轴承，k1与b不宜过大；不同倾角下，最小名义膜厚随渐扩形参数的变化趋势相似，因此对于轴颈倾斜的轴承可参照无倾斜轴颈轴承选取渐扩形参数。