基于频域高阶Rankine源法的有航速船舶斜浪中六自由度运动数值计算研究
杨云涛,朱仁传,陆 安,高 慧
(1.江苏科技大学船舶与建筑工程学院,江苏张家港 215600;2.上海交通大学船舶海洋与建筑工程学院海洋工程国家重点实验室,上海 200240)
0 引 言
船舶在海洋环境中航行时,不可避免地会遭遇来自不同方向的波浪。此时,船舶除了以某一平均速度的前进运动外,在波浪的激励下还会产生六自由度的摇荡运动。严重的摇荡运动不仅会影响船舶维持其正常使用功能的能力,在某些极端情况下甚至会造成船体倾覆或损毁。因此,开展船-波作用水动力问题研究,准确可靠地预报船舶在波浪中航行时的运动响应,对船舶的设计、使用以及航行安全等具有重要意义。
研究船舶这类大尺度物体在波浪作用下的运动响应时,流体粘性和船体曲率突变处的旋涡分离影响通常是局部、次要的,势流模型是对该问题的一个合理简化和近似。在过去的几十年中,基于势流理论的切片法[1]因其计算快捷、稳定且易于实现等优势,在船舶运动响应计算中应用广泛。但是该方法是在诸多假定的基础上建立的,对于高速、低频以及存在外飘的肥大船型,其数值预报结果的精度往往差强人意[2]。为了克服这些缺陷,近年来随着计算机技术的快速发展,出现了大量关于三维势流方法的研究工作,这些三维方法通常可以分为自由面格林函数法和Rankine源法两类。自由面格林函数法采用自动满足以辐射和均流线性化自由面条件的格林函数为边界积分方程的核函数,数值求解时只需要在物面布源,离散量较小,是目前解决零航速船-波作用问题的一种有效方法[3]。但是当船舶以一定的航速在波浪中航行时,该方法存在一定的局限性:由于有航速自由面格林函数存在高频振荡特性,因而数值计算复杂且对存在外飘的非直壁船型会出现计算不稳定现象[4];满足的是均流线性化自由面条件,无法考虑船体定常绕流对非定常扰动的耦合影响;在某些特殊的频率下,计算失效、无法得到可靠的数值解,出现所谓的不规则频率现象[5]。
采用以Laplace 方程的基本解1/r为核函数的Rankine 源法可以克服自由面格林函数法的这些局限。根据对时间因子处理方式的不同,Rankine 源法可以分为时域和频域法。由于时域Rankine 具有使用灵活、可采用只含速度势一阶导数的自由面的运动学和动力学条件等优势[6],被广泛应用于船舶在波浪中运动问题的研究。但从公开发表的文献[7-9]来看,这些研究大多针对的是船舶迎浪航行时的垂荡和纵摇运动。实际上,船舶在海上多为斜浪航行,伴随着六个自由度的耦合摇荡运动(包括纵荡、横荡、垂荡、横摇、纵摇和首摇),在采用上述时域Rankine源法进行数值模拟时,存在纵荡、横荡和首摇模态缺少回复力的问题[10]。为了解决这一问题,学者们[11]提出了引入人工弹簧模型的方法,但该方法的模拟精度仍有待进一步提高。相比时域,频域模型不存在没有回复力的问题,更适合斜浪中船舶运动响应计算,且计算效率也更高。但是,由于在Brard 数小于0.25 时难以处理船前产生波浪反射等原因[12],目前关于频域Rankine源法的研究大多局限于高航速或高频的迎浪工况。
本文针对船舶在斜浪中航行时的水动力学问题,在频域势流理论框架下,基于高阶Rankine 源法建立考虑定常绕流和横摇粘性阻尼影响的摇荡运动响应计算模型。数值实现时,在自由面条件中引入Rayleigh 人工阻尼,并采用二阶迎风差分格式进行离散处理,以保证辐射条件得到满足;在物面条件采用计及定常扰动势的mj项,并利用积分法进行求解,以提高数值计算的精度;采用CFD 方法模拟船舶的自由横摇衰减运动,并根据能量法计算粘性阻尼系数,代入运动方程求解运动响应,以避免势流理论无法考虑流体粘性所造成的横摇运动计算误差。在此基础上,采用Fortran自主开发数值程序,对不同船型在规则波中以不同遭遇浪向航行时的六自由度运动响应进行数值计算,并对其结果进行分析。
1 斜浪中航行船舶运动的频域势流模型
1.1 坐标系统和摇荡运动定义
设船舶以平均速度U和遭遇浪向β在波幅为A、圆频率为ω0、波数为k的深水规则波中斜浪航行(存在色散关系2=gk,其中g为重力加速度),建立图1 所示的两组右手坐标系:坐标系o-xyz为以船速U移动、原点位于静水面、x轴指向船舶前进方向、z轴竖直向上并通过平衡状态船舶重心的参考坐标系;坐标系ob-xbybzb为固定于船体、在平衡状态时与参考坐标系重合的动坐标系。在参考坐标系中,船上实际感受到的入射波频率变为遭遇频率ωe=ω0-kUcosβ,船舶在波浪激励下产生的摇荡运动可以分解为重心沿三个坐标轴的直线运动(纵荡X1、横荡X2和垂荡X3)以及动坐标绕三个坐标轴的转动(横摇X4、纵摇X5和首摇X6)。
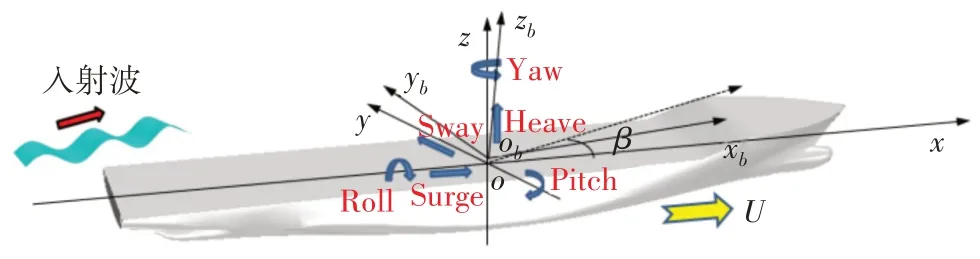
图1 坐标系统和摇荡运动Fig.1 Coordinate systems and ship motions
1.2 速度势及其边值问题
研究船舶在波浪中的运动问题时,流体(即水)可以看作是均匀、不可压缩且无粘的理想流体,流动可以认为是无旋的。此时,流场中任意一点的速度可以通过引入势函数Φ(x,y,z,t)来表示。在频域框架下,速度势Φ可以分解为
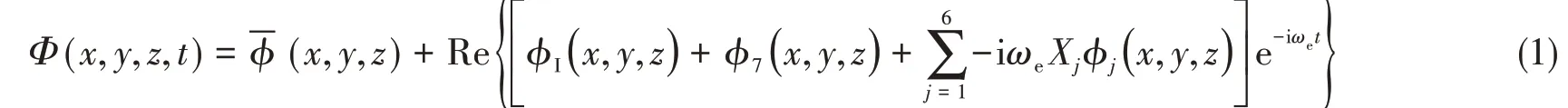
式中:右端第一项ˉϕ(x,y,z)为船舶定常运动的扰动势;剩余三项为非定常扰动势,其中ϕI和ϕ7分别为非定常入射势和绕射势的空间部分,ϕj(j=1,2,…,6)为船舶在j方向以单位速度摇荡产生的规范化辐射势。
对于定常扰动势ˉϕ(x,y,z),在一阶近似范围内可采用叠模流势代替[13],它在流域内满足Laplace方程

在线性波理论中,ϕI的表达式为

至于速度势ϕj(j=1,2,…,7),以往为了简便起见,通常对其进行求解时假定定常扰动势ˉϕ为小量,忽略船舶定常绕流的影响。但这一假定只适用于船体细长、前进速度是低速的情况。为了提高计算精度,本文在自由面和物面条件中计及ˉϕ的影响,采用以下定解条件:

式中:r=(x,y,z)为位置矢量。
1.3 非定常流体作用力和六自由度运动方程
船舶在波浪中航行时受到的外力按是否随时间变化可以分为定常力和非定常力。其中定常力主要包括重力、静浮力、推进力以及定常阻力,它们之间互相平衡,不会引起船舶的摇荡运动。因此讨论船舶在波浪中的运动问题时,只需要分析作用在船体上的非定常力。
若假定流体是无旋的理想流体,非定常流体作用力可通过利用Bernoulli方程和式(1)的速度势分解计算压强并沿船体湿表面积分求得,它可以分为入射力FIi、绕射力FDi、辐射力FRi和静恢复力FSi四个部分:

上述理想流体(无粘)假定在多数情况都是合理的,但是当船舶存在横摇运动时,由于粘性对其影响较大,还需考虑粘性力的作用。通常粘性力是非线性的,但可以采用如下等效线性化的形式表示:

2 数值实现

2.1 基于高阶Rankine源法计算绕辐射势
由于绕辐射势ϕj满足以Laplace 方程为控制方程的边值问题(6),根据格林第三公式,它可以采用如下的边界积分方程进行求解:


为了克服传统常值单元离散所存在的变量在边界上不连续、离散量大(计算效率低)以及难以获得精确的物面导数等缺陷,本文采用图2所示的9 节点二次单元对船体表面进行离散。经过上述的离散化处理,并将方程(6)中的自由面和物面条件代入式(14),可得如下的离散边界积分方程组:

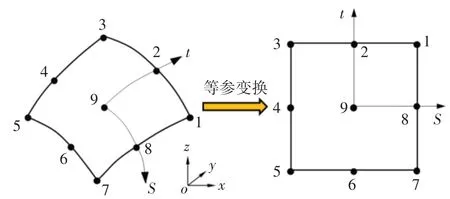
图2 9节点二次单元Fig.2 9-node bi-quadratic element
式中:NB和NF分别代表离散船体表面和自由面的单元数;Nk(s,t)和J(s,t)分别为形函数和Jacobian 矩阵,它们的表达式见文献[17]。
求解上述方程组的关键在于mj项的计算和ℑ[ˉϕ,ϕj]中ϕj的二阶空间导数的处理。根据公式(7)可知,mj取决于定常扰动势ˉϕ的一阶和二阶梯度,其中一阶梯度易于计算(在采用源分布法确定源强后,对定常扰动势的边界积分方程求梯度即可获得ˉϕ的一阶梯度),难点在于二阶梯度的求解。鉴于传统的直接数值差分法数值实现困难且精度不高[18],本文采用间接的积分法对ˉϕ的二阶梯度进行计算[14]。该方法将ˉϕ沿三个坐标轴的偏导数看作未知变量,建立关于它们的控制方程和边界条件,然后采用Rankine源法构建边界积分方程:

至于ℑ[ˉϕ,ϕj]中ϕj的二阶空间导数,为了反映流体相对船舶自上游流向下游(波动在上游衰减快,在下游衰减慢)的特征,保证数值计算的稳定性和精确性,本文采用如下的二阶迎风差分格式:

式中:i为自由面上离散单元节点的编号,它的数值从下游往上游逐渐增大;Ci、Ci+1、Ci+2和Ci+3为迎风差分格式的系数,它们的表达式见文献[19]。
2.2 基于CFD法计算横摇阻尼系数
当船舶斜浪航行时,会产生横摇运动。横摇受流体粘性影响较大,在采用频域运动方程(13)计算它的数值时,除了需要计及兴波阻尼系数外,还需要补充额外的横摇粘性阻尼系数。而后者是无法基于前文所述的频域势流理论求得的。目前,模型试验是估算横摇阻尼最为可靠的方法,但该方法存在成本高、速度慢以及换算到实船存在尺度效应等缺陷。随着计算机技术以及数值算法的快速发展,CFD 方法已成为研究船舶水动力问题的一种重要数值手段。CFD 方法相比模型试验更为经济、高效,相比势流方法可以考虑流体粘性。鉴于此,本文将采用CFD方法,通过仿试验的方式获得船舶自由横摇衰减曲线,在此基础上通过数值处理获得横摇阻尼系数。
CFD 方法模拟船舶自由横摇衰减运动所采用的控制方程、初始和边界条件、计算域范围、网格尺寸以及时间步等参数按照本文作者公开发表的文献[20]中的建议来设置。为了避免直接处理数值结果所产生的不稳定性,采用如下的衰减函数[21]拟合横摇衰减曲线:

式中,AD为横摇衰减曲线的最大横摇幅值,βi为衰减系数项,ωD为横摇衰减运动固有频率,ε为相位角。
根据能量守恒定律,船舶在自由横摇衰减过程中,ti到ti+1时间段内总能量的变化应等于阻尼力矩所做的功。由此可以推得[22]



在基于CFD法确定了横摇阻尼系数之后,本文进一步根据上一节的高阶Rankine源法开发数值程序计算绕辐射势,求解水动力系数和波浪力,并将其代入频域运动方程(13)便可求得船舶的六自由度运动响应。
3 数值方法验证
为了验证本文数值方法和程序的可靠性,以ITTC 标准船模S175 集装箱船为对象,开展船舶在首斜浪(β=150°)中垂荡、纵摇和横摇运动响应预报研究。S175 的船长L=175 m,船宽B=25.4 m,吃水D=9.5 m,排水量Δ=247 42 t,纵摇惯性半径kyy=0.24L,横摇惯性半径kxx=0.328B。

图3 S175自由横摇衰减运动计算网格Fig.3 Meshes used for the numerical simulation of roll delay motion of S175
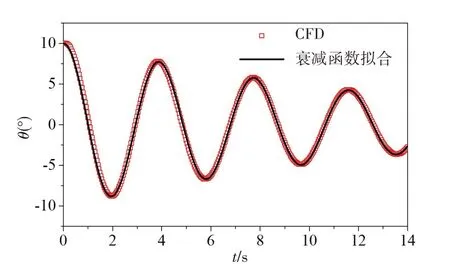
图4 S175自由横摇衰减曲线Fig.4 Free roll decay curve of S175
将采用CFD 法确定的横摇阻尼系数输入基于频域高阶Rankine 源法开发的数值程序,对S175 以航速Fr=0.275、遭遇浪向β=150°在规则波中航行时的运动响应进行预报。数值预报采用如图5 所示的经过收敛性分析的计算域和网格:自由面边界距船体1.5倍遭遇波长(λe=2πg/ω2e),单位遭遇波长内的网格节点数为20(自由面网格在数值程序中自动生成),船体网格的节点数为682。
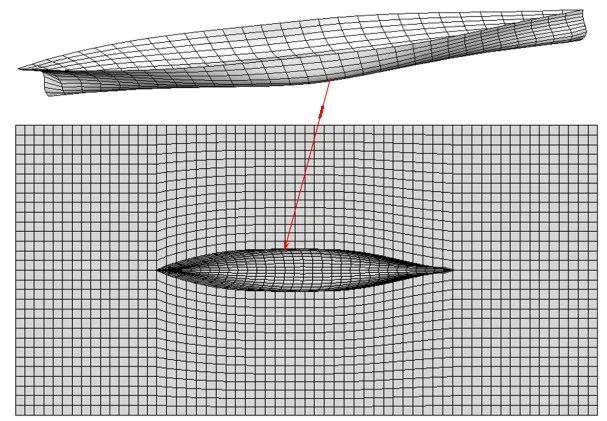
图5 S175船体和自由面网格划分示意图Fig.5 Mesh of S175 and free surface
图6给出了采用上述网格计算得到的垂荡、横摇和纵摇运动响应随入射波长的变化曲线(红色实线)。为了进行比较,图中还包含了试验值[24]以及本文作者建立的移动脉动源[4]和半解析高阶移动脉动源[25]的数值计算结果。移动脉动源法和半解析高阶移动脉动源法在求解势流问题时都是以移动脉动源格林函数为边界积分方程的核函数,其中前者在以常值元离散边界的基础上,采用传统的高斯求积公式计算格林函数的面积分;而后者选择了与本文相同的高阶单元离散边界,且为了避免格林函数沿水平方向的高频振荡所引起的数值计算的不稳定,采用了一种半解析的公式计算格林函数的面积分。从图中的结果可以看出,本文的频域高阶Rankine源法和另外两种数值方法计算得到的运动响应结果与试验值的变化趋势基本是一致的。但由于本文方法采用的核函数1/r计算简单且不存在振荡性,相比移动脉动源法,计算更为稳定(尤其是纵摇运动);由于在自由面和物面条件中考虑了船舶定常绕流的影响,相比基于均流线性化自由面条件的半解析高阶移动脉动源法,预报的垂荡和纵摇运动响应的结果在峰值附近与试验值更为接近。
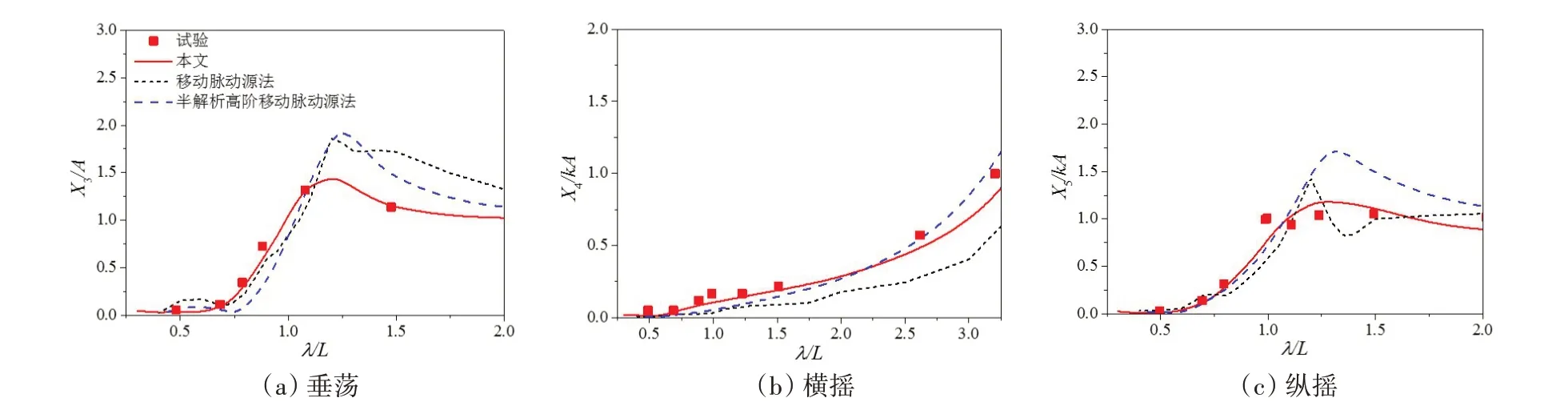
图6 S175以航速Fr=0.275、遭遇浪向β=150°在规则波中航行时的运动响应Fig.6 Motion responses of S175 at Fr=0.275 with heading angle β=150°
4 不同浪向下船舶六自由度摇荡运动数值模拟与分析
上述对S175船在遭遇浪向β=150°时的垂荡、横摇和纵摇运动的预报证实了本文建立的频域高阶Rankine在斜浪运动响应计算中的可靠性。在此基础上,下面进一步对不同浪向下船舶的六自由度摇荡运动进行模拟与分析。计算船型除了细长的S175 集装箱船,还包括一艘在KVLCC2 基础上改进得到的方形系数CB=0.84的散货船S-Cb84[26]。
4.1 S175船
图7给出了S175以Fr=0.275在不同浪向的规则波中航行时运动响应的计算结果与已有试验值[24]的比较。除了两个首斜浪(β=120°和150°)下六自由度摇荡运动RAO,图中还包括了横浪时S175的横荡、垂荡和横摇运动结果。由图可以看出,数值计算结果与已有试验值吻合良好,表明本文方法适用于不同浪向下船舶运动响应的预报。比较三个不同浪向下S175的运动RAO曲线可以发现,它们随入射波长的变化趋势类似,但是曲线峰值(即运动共振)对应的波长会随着浪向角的减小逐渐减小(垂荡和纵摇最为明显)。这主要是因为当船舶以一定的航速在波浪中航行时,波浪是以遭遇频率的振荡规律作用于船舶,运动共振发生在遭遇频率等于固有频率的工况。根据遭遇频率的表达式ωe=ω0-kUcosβ可知,它是随航速U、浪向角β和入射波频率ω0(或波长)而变化的,当船舶以一定的航速在首斜浪中航行时,若浪向角β较小,则入射波频率ω0必须较大时(即波长较小)才能使得遭遇频率ωe等于固有频率。

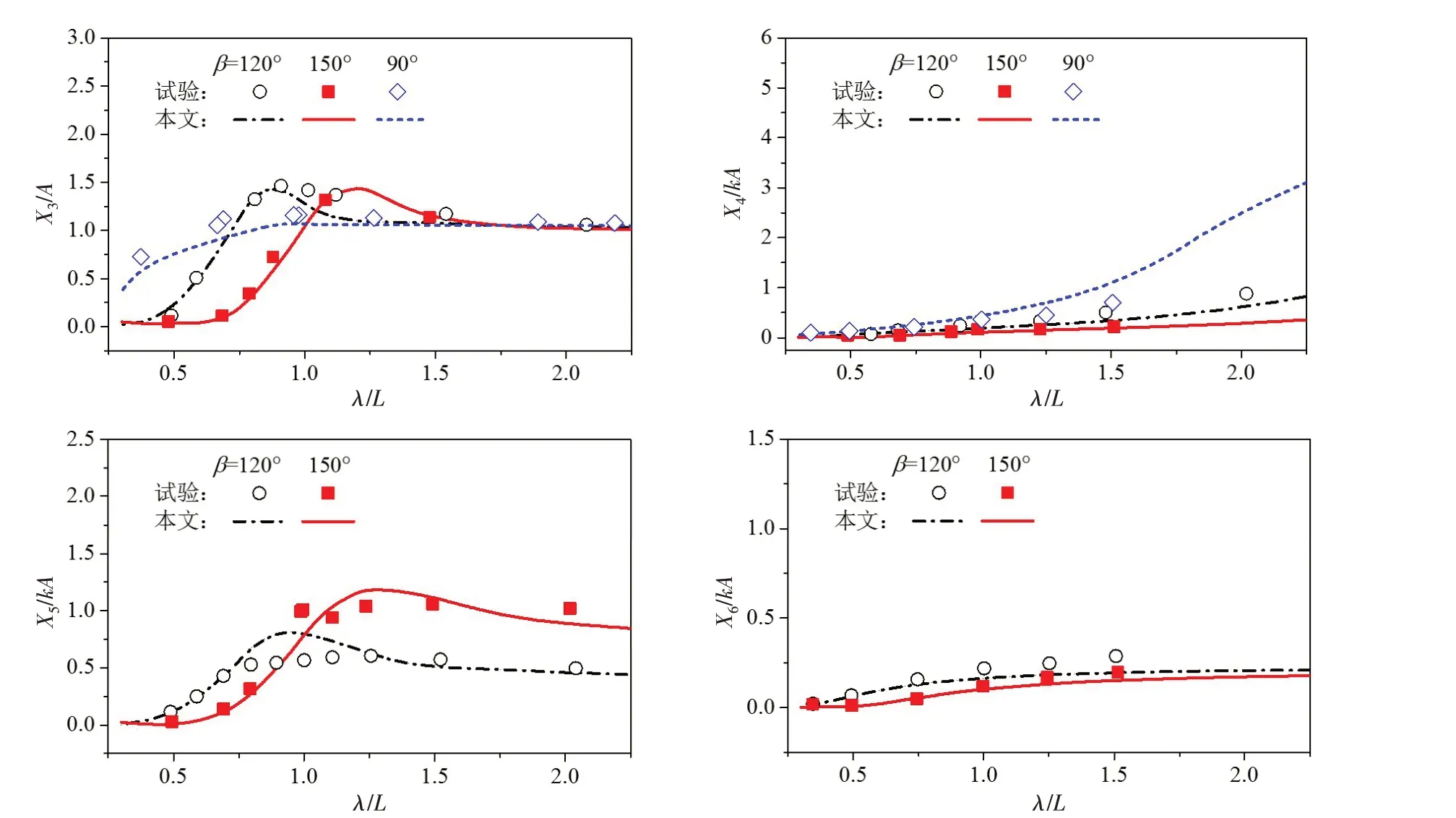
图7 S175以航速Fr=0.275在不同浪向的规则波中航行时的运动响应Fig.7 Motion responses of S175 at Fr=0.275 with different heading angles
4.2 S-Cb84散货船
采用本文方法进一步对较为肥大的散货船S-Cb84 的运动响应进行计算。S-Cb84 的主尺度为:船长L=320 m,船宽B=58 m,吃水D=20.8 m,排水量Δ=324 000 t,纵摇惯性半径kyy=0.25L,横摇惯性半径kxx=0.35B。图8 为运动响应计算中采用的船体网格(节点数为962),自由面网格参数的设置策略与S175相同。
图8 S-Cb84运动响应计算采用的船体网格Fig.8 Meshes of S-Cb84 used in the calculation of motion responses
图9给出了S-Cb84以航速Fr=0.099在首斜浪β=150°和尾斜浪β=30°中航行时,六自由度运动响应随入射波长的变化。对比数值结果和试验值可以看出,无论是首斜浪还是尾斜浪,本文方法均可以较好地预报出S-Cb84的运动响应。
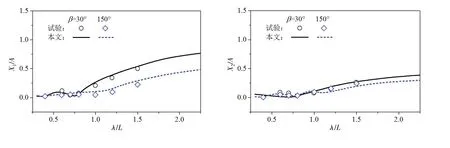

图9 S-Cb84以航速Fr=0.099在首斜浪β=150°和尾斜浪β=30°中航行时的运动响应Fig.9 Motion responses of S-Cb84 at Fr=0.275 with heading angles β=150°and 30°
图10进一步给出了横浪时,在数值计算中分别考虑和不考虑横摇粘性阻尼的横摇和垂荡运动响应结果的对比。可以发现,对于垂荡运动,是否考虑横摇粘性阻尼,结果几乎没有差别;但是对于横摇运动,若忽略粘性阻尼的影响,本文基于频域高阶Rankine 源法的数值计算程序将会严重高估共振频率附近的运动响应。
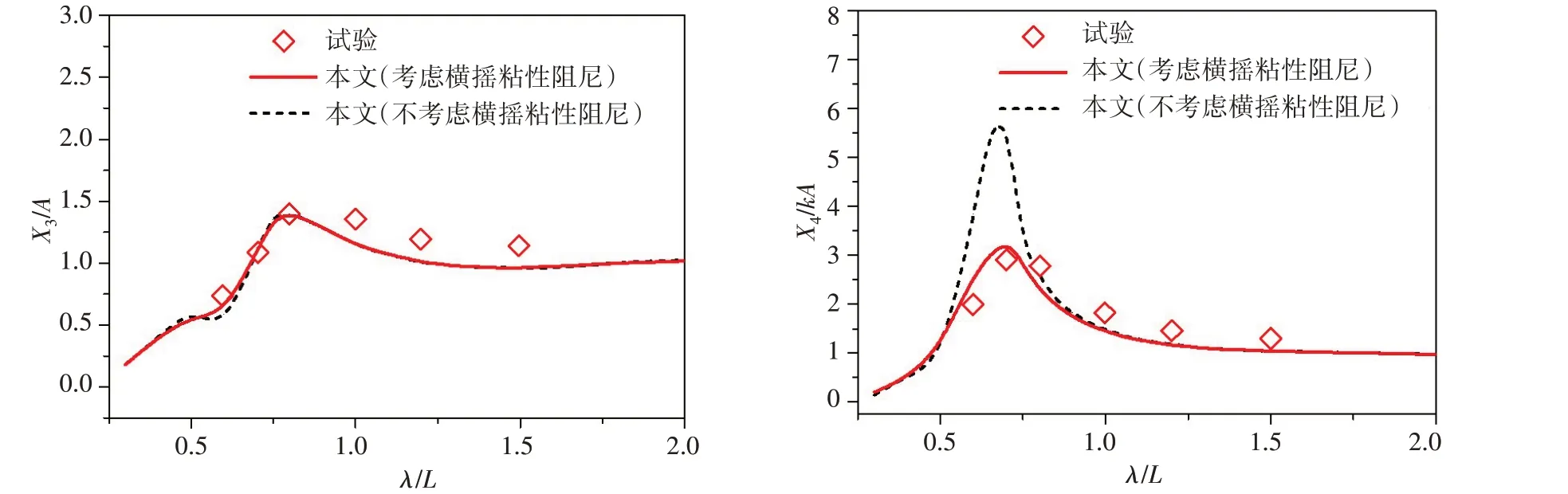
图10 横浪下(β=90°)考虑和不考虑横摇粘性阻尼的S-Cb84垂荡和横摇运动响应计算结果对比Fig.10 Comparison between the results of heave and roll motion responses calculated by considering and neglecting the influence of viscous roll damping of S-Cb84 in beam waves(β=90°)
5 结 论
本文针对船舶在海上斜浪航行时的水动力学问题,基于频域高阶Rankine源法并结合CFD技术获得的横摇粘性阻尼系数,建立了预报船舶六自由度摇荡运动响应的数值方法和程序。通过对不同船型在不同浪向和波长规则波中运动RAO的数值计算和分析,得出以下结论:
(1)对于横摇运动,流体粘性影响显著,忽略横摇粘性阻尼会严重高估共振频率附近的运动响应。本文采用CFD法模拟船舶自由横摇衰减运动,经能量法处理获得横摇阻尼系数,将其与频域高阶Rankine源法相结合可以更为准确地预报横摇运动RAO;
(2)相比基于移动脉动源格林函数的数值方法,由于本文方法在求解绕辐射势时采用了简单易于计算的Rankine源1/r,并且在自由面条件中计入了船舶定常扰流的耦合影响,计算更为稳定且运动响应的预报结果在峰值附近与试验值更为接近;
(3)无论是细长的集装箱船S175,还是肥大的散货船S-Cb84,数值模拟得到的不同浪向下六自由度运动响应结果均与试验值吻合良好,表明本文建立的数值方法在斜浪航行船舶摇荡运动预报中,对于不同船型、不同浪向均有广泛的适用性。

