伊藤随机马尔可夫跳变奇异系统控制设计
谢 俊,周绍生
(1.杭州电子科技大学理学院,浙江 杭州 310018;2.杭州电子科技大学自动化学院,浙江 杭州 310018)
0 引 言
伊藤随机马尔可夫跳变系统可以很好地描述不同类型的突变情况,引起国内外学者的广泛关注。文献[1]研究具有时变转移率的连续时间伊藤随机马尔可夫跳变线性系统的稳定性与镇定问题,运用随机李雅普诺夫函数和矩阵解耦方法得到了系统稳定的充分条件。文献[2]采用线积分型LK泛函方法研究带有时滞的伊藤随机区间二型系统的随机渐近稳定性、广义耗散性和状态反馈控制问题,采用锥补线性化方法和高阶矩阵解耦方法得到使系统满足随机渐近稳定和广义耗散性的充分条件。文献[3]运用T-S模糊模型研究一类非线性连续半马尔可夫跳变奇异系统的有限时间静态输出反馈H∞控制问题,采用随机李雅普诺夫函数方法和矩阵不等式解耦技术,得到闭环系统奇异随机H∞有限时间有界性的线性矩阵不等式条件。文献[4]研究一类非齐次马尔可夫跳变随机奇异区间二型系统的随机容许和镇定问题,构造随机李雅普诺夫函数,采用广义伊藤公式及不等式放缩技术给出系统随机容许的充分条件。本文在文献[1]和文献[4]的基础上,运用随机李雅普诺夫函数和Finsler引理研究了伊藤随机马尔可夫跳变奇异系统的随机容许性、H∞性能等问题,并设计了静态输出反馈控制器。
1 系统描述
假设连续时间伊藤随机马尔可夫跳变奇异系统如下:


(1)
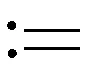
(2)

(3)



(4)

通过模糊混合,区间二型模糊系统可描述如下:
(5)
针对模型(5),本文设计了一个前提匹配的静态输出反馈控制器,模糊规则如下:

u(t)=Ki(rt,φt)y(t)
通过模糊混合,静态输出反馈模糊控制器表示如下:
(6)
将控制器(6)代入系统(5),得到闭环系统如下:
(7)
式中,
Aijk(rt,φt)=Ai(rt)+B1i(rt)Kj(rt,φt)C1k(rt),Bijk(rt,φt)=B2i(rt)+B1i(rt)Kj(rt,φt)C2k(rt),
C1ijk(rt,φt)=L1i(rt)+L2i(rt)Kj(rt,φt)C1k(rt),C2ijk(rt,φt)=L3i(rt)+L2i(rt)Kj(rt,φt)C2k(rt).


引理2[6](Finsler引理)设G=GT∈Rn×n,η∈Rn和U∈Rn×n且rank(U) 其中,U⊥表示U的右零空间的基构成的列满秩矩阵。 定义1[7]在零初始条件下,对于任何非零ω(t)∈L2[0,+∞),闭环系统(7)若满足 (8) 则称闭环系统(7)满足H∞性能。 本文运用随机李雅普诺夫函数建立使闭环系统(7)满足H∞性能和随机容许性的充分条件。 定理1对于∀i,j,k∈S,α∈N,m∈M,如果存在矩阵Pα m使得下列不等式成立, (9) (10) 则闭环区间二型模糊系统(7)是随机容许的且具有H∞性能。 证明由式(9)和式(10)可知, 参照文献[7]中引理1的证明可知,当ω(0)=0时,系统(7)是正则的、无脉冲的。 若rt=α,φt=m,随机李雅普诺夫函数为: 所以,总存在一个充分小的常数c>0使得 再运用Dynkin公式,可得: E[V(x0,r0,φ0)],∀t>0 所以,当ω(0)=0时,系统(7)是随机稳定的。 假设初始条件为0,即x(0)=0,并定义 由Dynkin公式及V(x0,r0,φ0)=0,可得 参照文献[7]可得JT1<0,不等式(8)成立,即闭环系统(7)满足H∞性能。证毕。 本文运用Finsler引理设计一种使系统(7)满足随机容许性和H∞性能的静态输出反馈控制器。 (11) 式中, Aijkαm=Aiα+B1iαKjαmC1kα,Bijkαm=B2iα+B1iαKjαmC2kα,C1ijkαm=L1iα+L2iαKjαmC1kα, 则闭环区间二型模糊系统(7)是随机容许的且具有H∞性能。 证明由式(11)和文献[7],可得: (12) 式中, 参照文献[8],对式(12)使用引理2,可得: (13) 式中, (14) 式中, (15) 式中, 假设伊藤随机马尔可夫跳变奇异系统中i=2,α=2,其参数如下: L111=(-0.5 0.4),L112=(0.5 -0.5),L121=(0.6 -0.3),L122=(1.2 -0.5),L211=0.1, L212=0.2,L221=0.2,L222=0.3,L311=0.3,L312=0.1,L321=0.2,L322=-0.1, C111=(0.1 0.7),C112=(0.8 0.2),C121=(0.3 0.5),C122=(0.4 0.4),C211=-0.1,C212=0.1, 对定理2中的不等式(11)求解,得到一组可行解, K111=-3.248 9,K112=-2.645 4,K121=-0.581 5,K122=-0.657 8,K211=-3.098 7,K212=-2.645 4,K221=-0.572 6,K222=-0.657 8。 图1 闭环系统的状态响应x(t) 从图1可以看出,随着时间的变化,转移率矩阵的模态跳变信号在1和2之间来回跳跃;随机跳变过程中,0~3 s时,闭环系统是不稳定的,3 s后的闭环系统具有良好的稳定性。 本文研究一类连续时间伊藤随机马尔可夫跳变奇异系统满足H∞性能指标下的稳定性分析问题,并设计了满足闭环系统稳定性和H∞性能的静态输出反馈控制器。值得注意的是,静态输出反馈控制器的设计思路也可以用于解决动态输出反馈控制问题。后续将针对伊藤随机马尔可夫跳变奇异系统的L2—L∞性能、耗散性等问题展开进一步研究。
2 H∞性能分析





3 输出反馈控制器设计






4 数值仿真与分析



5 结束语

