高性能永磁同步发电机无位置传感器控制策略

刘忠永， 国敬， 范涛， 边元均， 孟柳， 章回炫， 温旭辉

(1.中国科学院大学, 北京 100049; 2.中国科学院 电工研究所, 北京 100190)

0 引言

在新一代军事技术变革持续推进的大背景下，集电驱动、电武器、电防护为一体的全电化研究已成为军事特种车辆的重要发展方向[1-2]，永磁同步发电机以其高功率密度，高峰值效率等优势成为特种车辆发电系统的绝佳选择。在当前应用最广泛的矢量控制技术中，精准的电机转子位置信息是保证高性能控制的必要前提，常见的获取转子位置信息的方法是通过光电编码器、旋转变压器等传感器进行测量，但其通常需要额外的空间及配套硬件设备，增加了系统的成本和复杂性。且在特种车辆复杂的运行工况及各类极端环境下，位置传感器的故障已成为发电系统中主要的故障发生源[3]。因此，为了提高系统功率密度，降低成本，进一步保障系统的稳定性，采用无位置传感器算法的永磁同步发电机控制策略逐渐成为研究热点，方法主要分为两类[4-5]：一是基于电机本身凸极性的转子位置估算方法，模拟旋转变压器的工作原理，通过注入高频正弦波或方波信号获取转子位置信息[6-10]，但该方法对于电机本体具有一定的要求，不适用于隐极机，适用范围较窄，额外的信号注入会增加电机涡流损耗、影响电机的控制性能；二是基于电机模型的估算方法，通过反电势、磁链等状态量获取转子位置信息，常见的方法有线性状态观测器法[11-12]、磁链估计法[13-14]、滑模观测器法[15-17]、扩展卡尔曼滤波器法等[18-19]，此类方法在中高速区域具有较好的动静态性能，但是在低速工作区内容易受噪声影响，且模型对于电机参数变化较为敏感，在大功率运行时受温度、电流等因素影响容易出现电感饱和现象，模型参数失配，影响位置观测精度，进而出现算法失稳的情况[20]。

针对上述问题，以特种车用发电系统为应用背景，本文提出一种全速度范围的永磁同步发电机无位置传感器控制策略。在低速工作区时，发电机尚未切入负载，采集三相电压通过正交锁相环获取转速及转子位置信息。当到达设定转速阈值时，切换到基于线性状态观测器的无位置传感器算法，完成发电动作并投切负载，并结合基于递推最小二乘的参数辨识算法[21-23]，将不同工况下的参数辨识结果反馈到观测器模型，克服了观测器算法易受电机参数影响的问题。全程由估算电机转速作为判定条件，实现特种车用发电系统全自动化控制，最终在30 kW电机对拖平台上完成了功率验证，实验结果证明了该控制策略的正确性和有效性。

1 无位置传感器控制策略

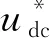
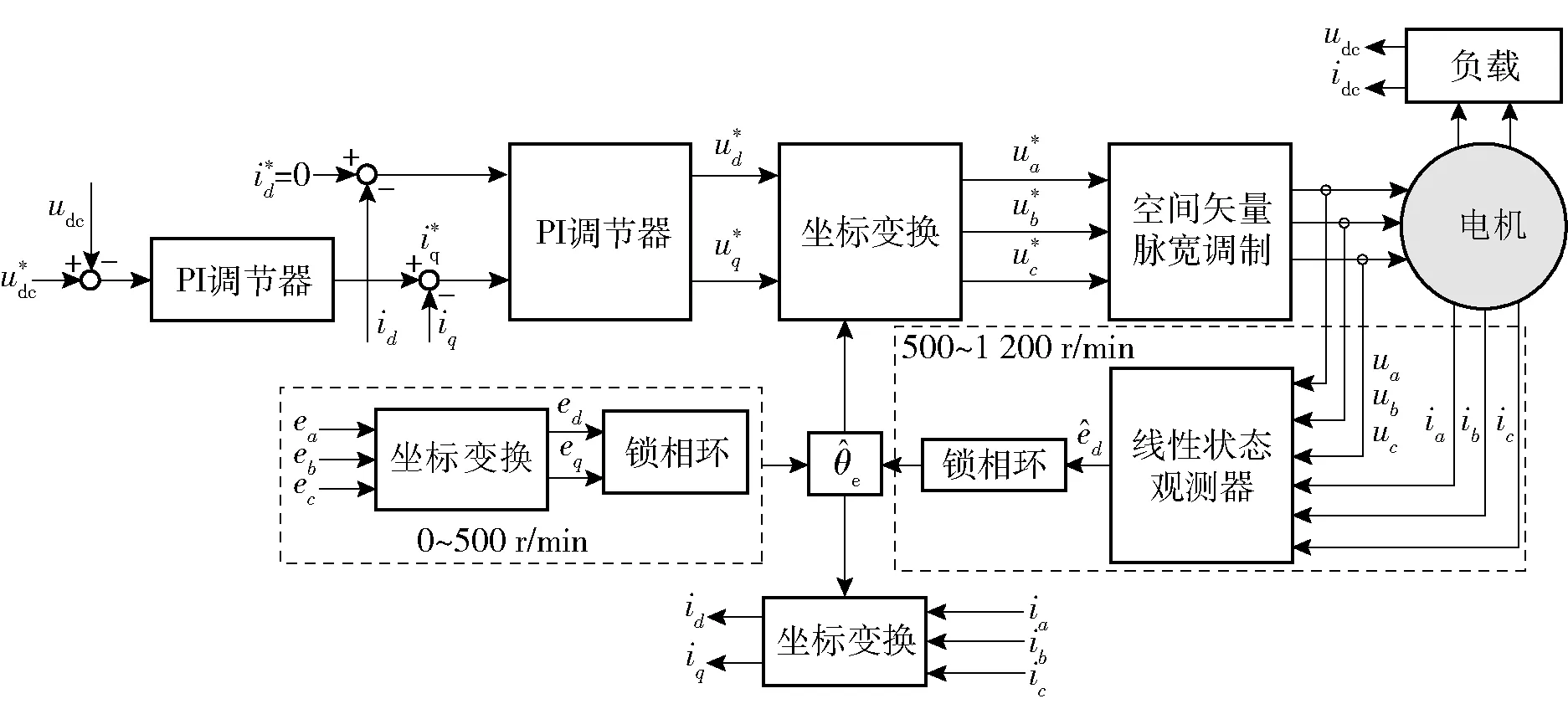
图1 无位置传感器发电策略控制框图

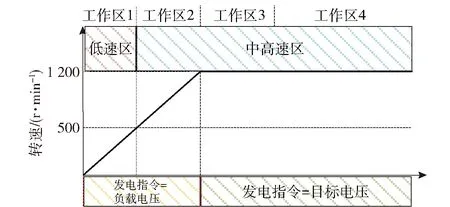
图2 全速度发电工况区域划分

由图1可知，基于PI调节器的永磁同步电机发电算法中，由无位置算法估算的转子位置信息e在两次坐标变换时被调用，算法实现流程如图3所示。当原动机拖动发电机旋转，程序开始运行时处于工作区1，将基于正交锁相环的角度跟踪器获取的估算位置信息e1赋值给e，此时系统给定的发电指令udccmd与直流侧反馈电压udcfb相同，当判定转速大于500(r/min)时，进入工作区2，此时转子位置信息e由基于线性状态观测器获取的估算位置信息e2所赋值；当判定转速大于1 200(r/min)时，进入工作区3，给定目标发电指令，即udccmd=udcobj，完成发电任务后在工作区4内进行负载投切。

图3 无位置传感器发电算法流程图

1.1 基于正交锁相环的转子位置观测算法

在工作区1内，发电机尚未切入负载，给定发电指令与反馈电压相同的控制策略，电压环PI调节器输出为0，即dq轴电流指令为0，忽略电阻压降，此时的相电压uabc即为反电势eabc，内含转子位置信息。由于逆变器输出电压为PWM波，需要通过硬件滤波电路实现相电压采集，本次实验逆变器开关频率10 kHz，设置滤波截止频率为3 kHz，实验所用电机12对极，工作区1内最高转速500 r/min对应电基频100 Hz，经滤波电路相位延迟1.8°，在误差允许范围之内，PWM波及滤波后电压波形如图4所示。逆变器工作时，为了防止桥臂上下管直通，需要在程序中加入死区时间，考虑死区的实际输出电压与理想输出相电压的平均电压误差与母线电压及死区时间呈正比，与开关频率呈反比[24]，在本次实验中死区时间给定3 μs，发电机在工作区1内低速运行，母线电压较低，理论上不会对三相电压采样产生明显影响，由于实验中无法将死区时间清零，现通过仿真进行验证分析，设置死区时间分别为0 μs与 3 μs，以及在逆变器模型中加入导通管压降的相电压对比如图5所示，可以看到三者几乎保持一致，即逆变器死区时间及管压降在该工况下不会影响三相电压采样精度。

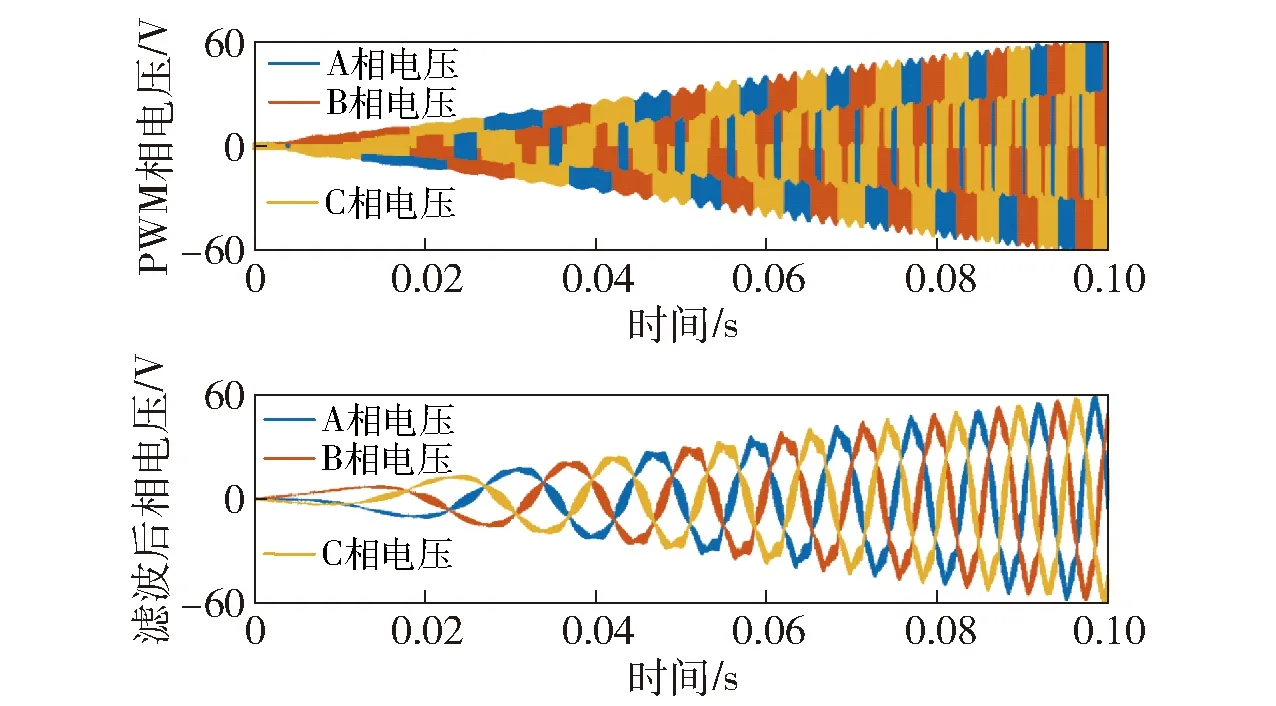
图4 PWM相电压及滤波后相电压

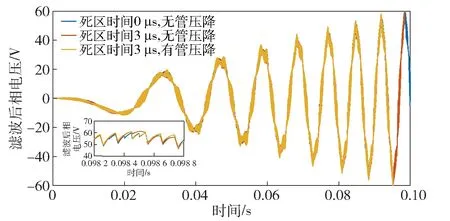
图5 不同死区时间下的相电压对比

获取三相反电势后，通过基于正交锁相环的角度跟踪器[25]获取转子位置信息，算法框图如图6所示，三相反电势经坐标变换至正交坐标系，与估算转子位置做差，当真实的转子位置θe与估算值e误差很小时，锁相环的误差收敛方程线性化如(1)式所示：

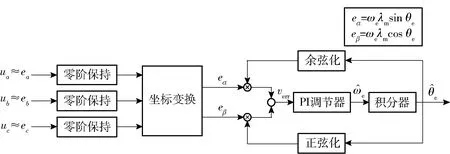
图6 基于正交锁相环的角度跟踪器

verr=ωeλmsinθecose-ωeλmcosθesine=

ωeλmsin(Δθe)≈ωeλmΔθe

(1)

锁相环线性化原理框图如图7所示，kp、ki为比例、积分增益系数。输入为真实转子位置，输出为估算转子位置，其本质是为一个单位积分环节设计指令跟踪调节器，系统及误差传递函数如(2)式～(3)式所示：

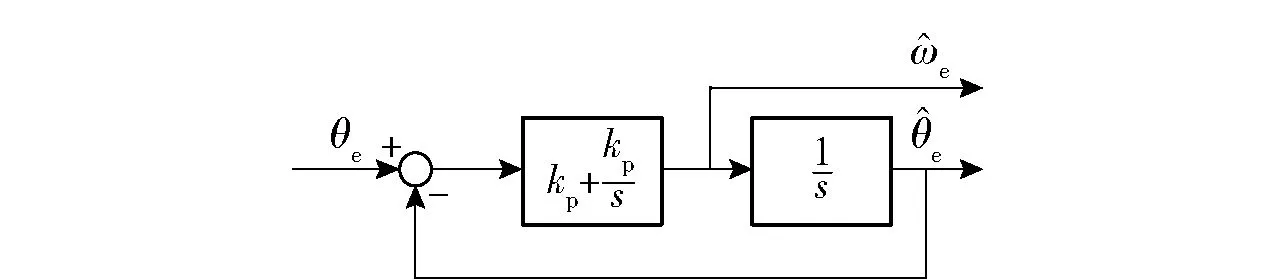
图7 锁相环线性化原理图

(2)

(3)

由图7可知，PLL为Ⅱ型系统，对于角度信号的阶跃输入信号及斜坡输入信号可以实现无静差跟踪，当输入为加速度信号，即θe=αt2时(α为转子加速度)，系统的稳态误差数学表达式如(4)式所示，此时可以看到虽然加速度信号输入存在误差，但是可通过调节积分增益系数ki来降低加速度输入下的稳态误差。

(4)

对系统传递函数进行分析，可知PLL实际上是标准二阶系统和其微分项的叠加，将(2)式写为经典传递函数的形式如(5)式所示。由于此时无零点部分本身已存在超调及振荡，后续微分环节在其峰值前后将加剧整个系统的振荡幅度，当积分系数ki增大时，系统的振荡幅度将随之增大；比例系数kp增大时，阻尼比增大，系统超调减小；由二阶系统频域动态特性分析可知，当阻尼比ζ不变时，增大积分系数ki，调节时间会缩短，系统伯德图及阶跃响应如图8～图9所示，可以看到在不同PI参数下系统的幅频特性及阶跃响应与上述分析一致。

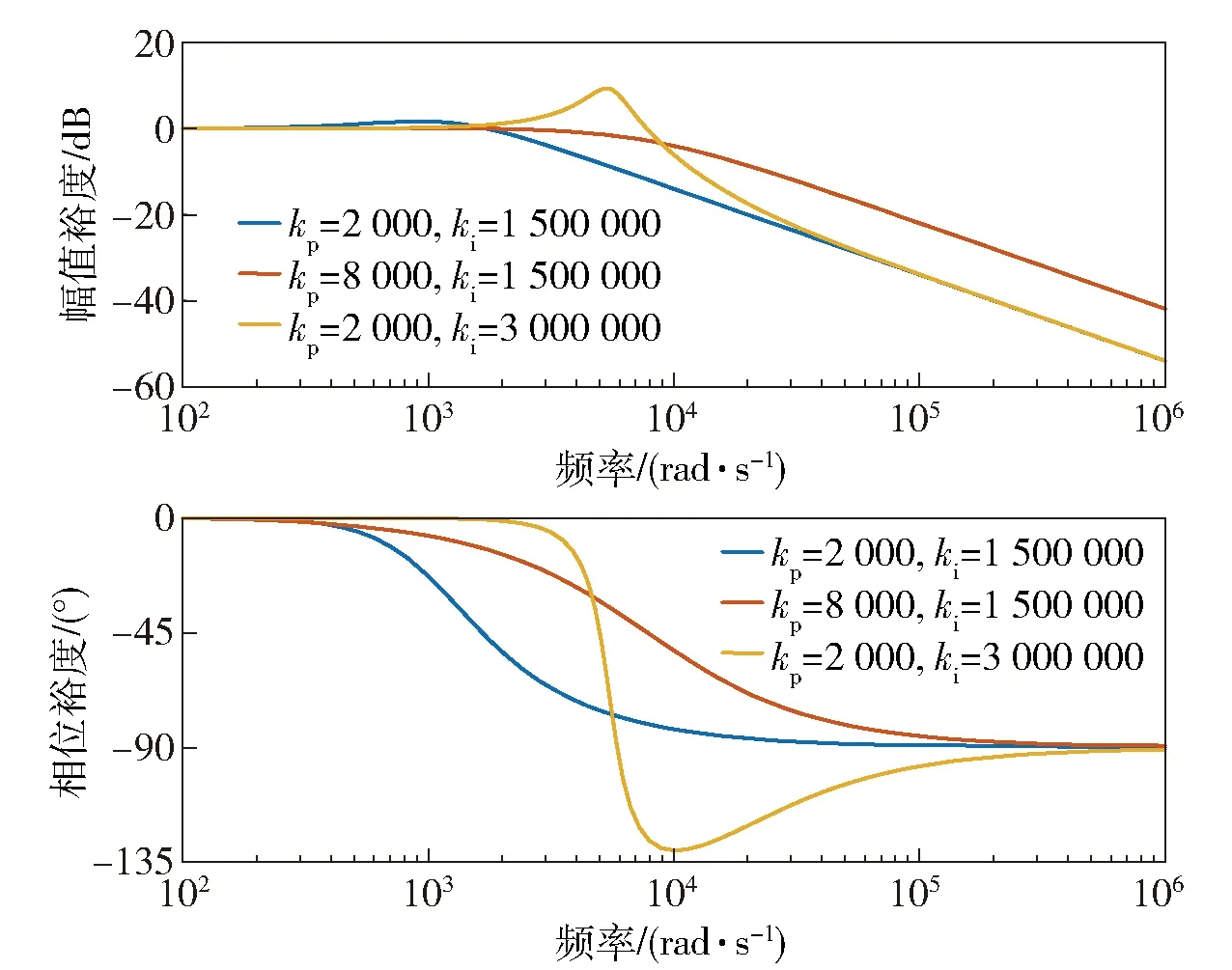
图8 锁相环伯德图

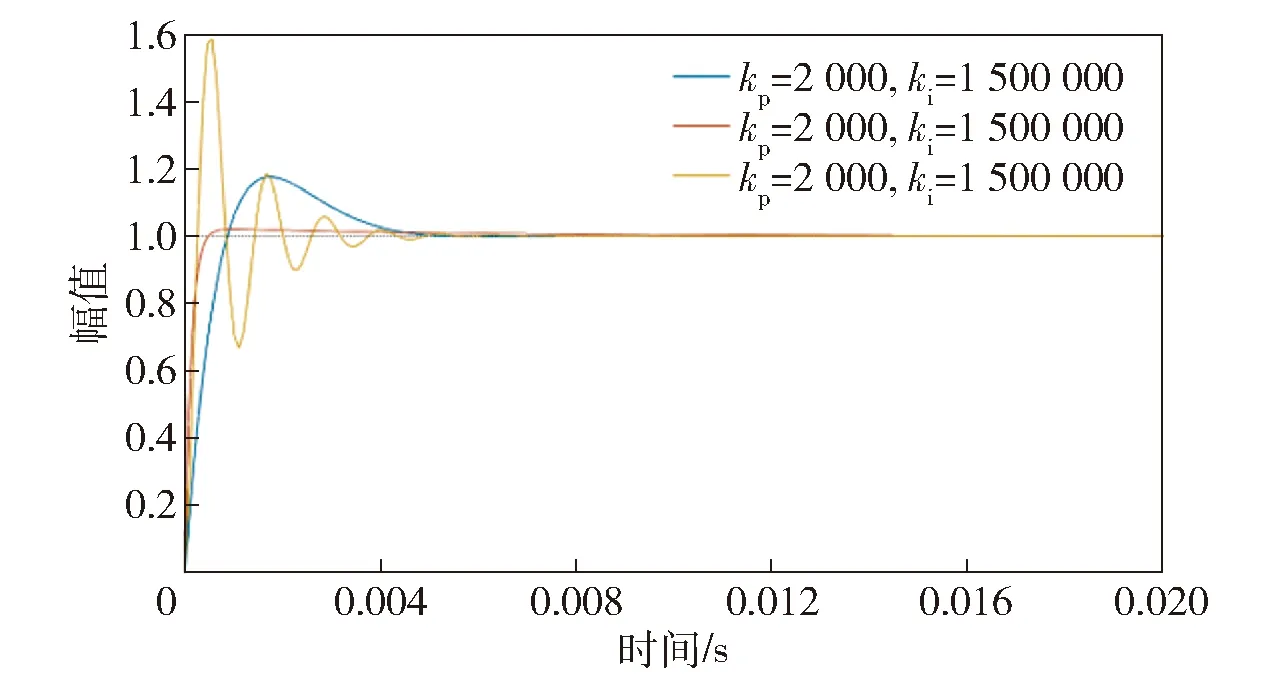
图9 锁相环阶跃响应图

(5)

1.2 线性状态观测器

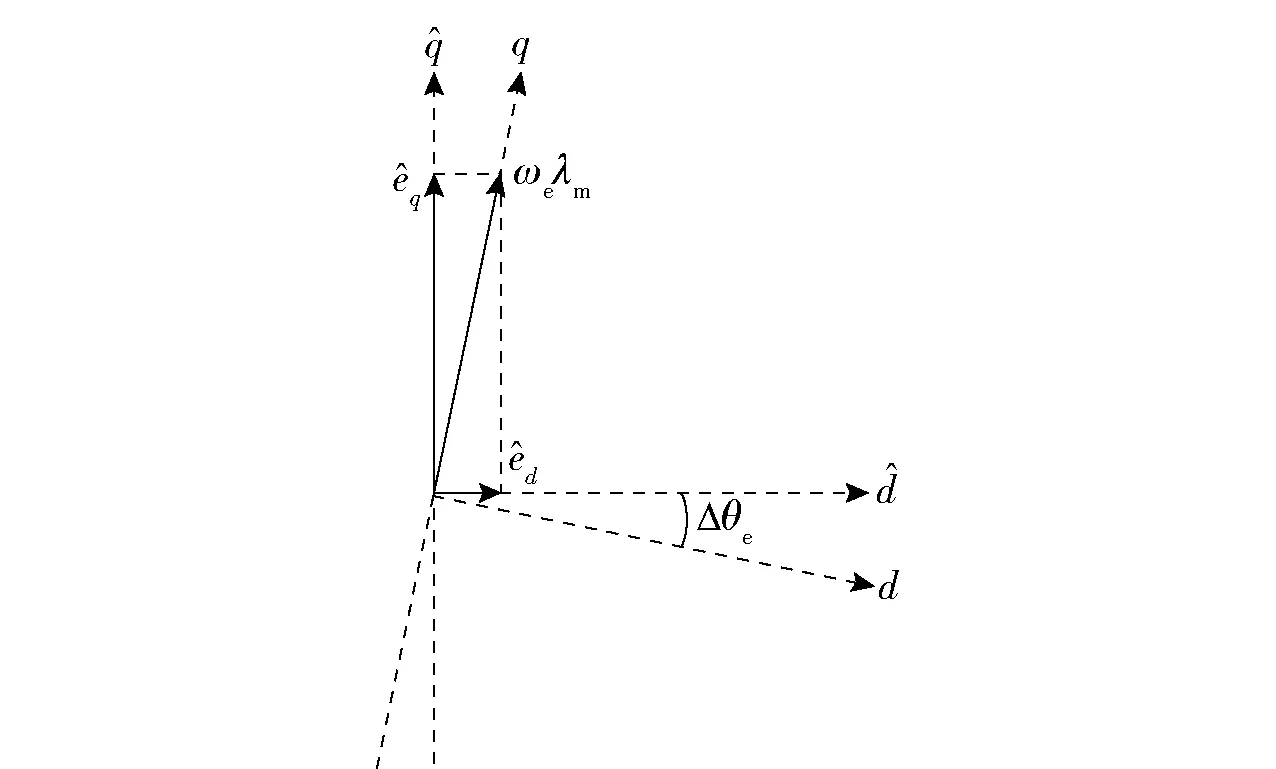
图10 永磁同步发电机旋转坐标系

(6)

状态观测器原理如图11所示，选取d、q轴电流及反电势观测值[dqdq]T作为状态变量x，选取dq轴电压[uduq]T作为输入变量u，选取d、q轴电流观测值[dq]T为输出变量y。需要注意的是由(6)式建立状态空间时，由于反电势中含有转速项，导致该状态空间方程受转速变化影响，直接求解反馈增益矩阵和配置极点时会遇到困难，但由于电机机械时间常数远大于电气时间常数，在一个控制周期内，可假设转子位置及转速为常数，即根据(7)式建立状态观测器的状态空间方程如(8)式所示[26-27]。

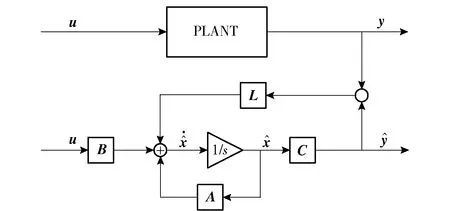
图11 线性状态观测器框图

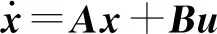
(7)

(8)

当引入反馈增益矩阵L后，观测器状态空间方程如(9)式所示：

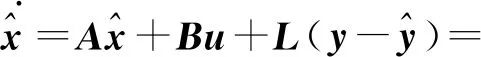
(9)

构建状态观测器与系统的误差函数如(10)式所示，由(11)式微分方程解析解可知，当矩阵[A-LC]特征值都在负半平面时，误差项可收敛至0，观测器的状态观测值趋于系统真值，根据极点配置法，需同时考虑系统收敛速度及抗扰能力设计合适的反馈增益矩阵。

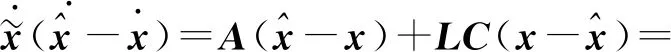
(10)

(11)

在dq坐标系下，为方便计算，将系统的特征方程配置成欠阻尼系统的形式如(12)式所示：

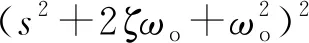
(12)

式中：ζ为系统阻尼比；ωo为观测器自然频率；I为单位矩阵。

考虑到旋转坐标系下的耦合项，配置反馈增益矩阵L如(13)式所示，可实现dq轴反电势的完全解耦。

(13)

将(13)式代入(9)式得到完整的状态空间方程，经离散化后如(14)式所示，在观测器获取反电势之后，对其进行线性化处理，通过基于锁相环的角度跟踪器获取转速，经积分环节后得到转子位置，反馈到状态观测器，参与控制形成闭环，算法框图如图12 所示。本节的锁相环与1.1节中的正交锁相环虽表现形式不同，但原理相同，此处不再做具体阐述。

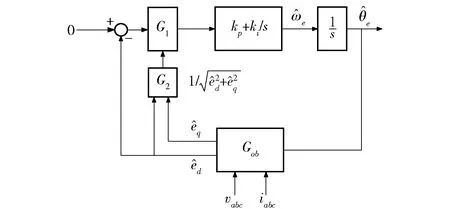
图12 基于锁相环的角度跟踪器

(14)

(15)

(16)

1.3 基于递推最小二乘的参数辨识算法

永磁同步发电机在不同的运行工况中，其参数受定子绕组电流、磁通饱和等因素影响，会在一定的范围内发生变化[28-29]，将直接影响到状态观测器的稳定状态，从而影响到电机控制性能。对电流环控制器设计来说，常见的辨识参数主要有4个，分别是定子电阻、永磁磁链、dq轴电感。对于无位置控制策略而言，在id=0的控制策略下，q轴电感随电流变化对算法的影响较为明显，本文采用递推最小二乘算法通过提前标定获取不同工况下的q轴电感参数，并通过在线查表的方式为状态观测器提供实时电机参数。

相较于一般的最小二乘法，递推最小二乘法的计算量小、收敛速度快，具有较明显的优势，最小二乘格式如(17)式所示：

(17)

在控制策略下，不考虑d轴电流带来的影响，(6)式电机方程离散化如(18)式所示，辨识模型如(19)式所示。

(18)

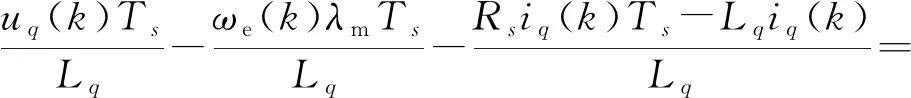
(19)

式中：输出向量y(k+1)=[iq(k+1)]，状态向量Φ(k)T=[uq(k)iq(k)ωe(k)]T，参数向量k=[abc]，本次实验中离线模式下辨识出的q轴电感参数如图13所示，可以看到q轴电感随着q轴电流增大而减小，此时状态观测器由于模型参数偏差，将产生相应的反电势观测误差，从而影响到估算的转子位置信息，导致磁场定向偏差，使得发电机电压极限圆发生旋转，电机转矩输出能力降低，损耗增大，运行效率降低，发电机带载能力降低，稳定性变差[30]。

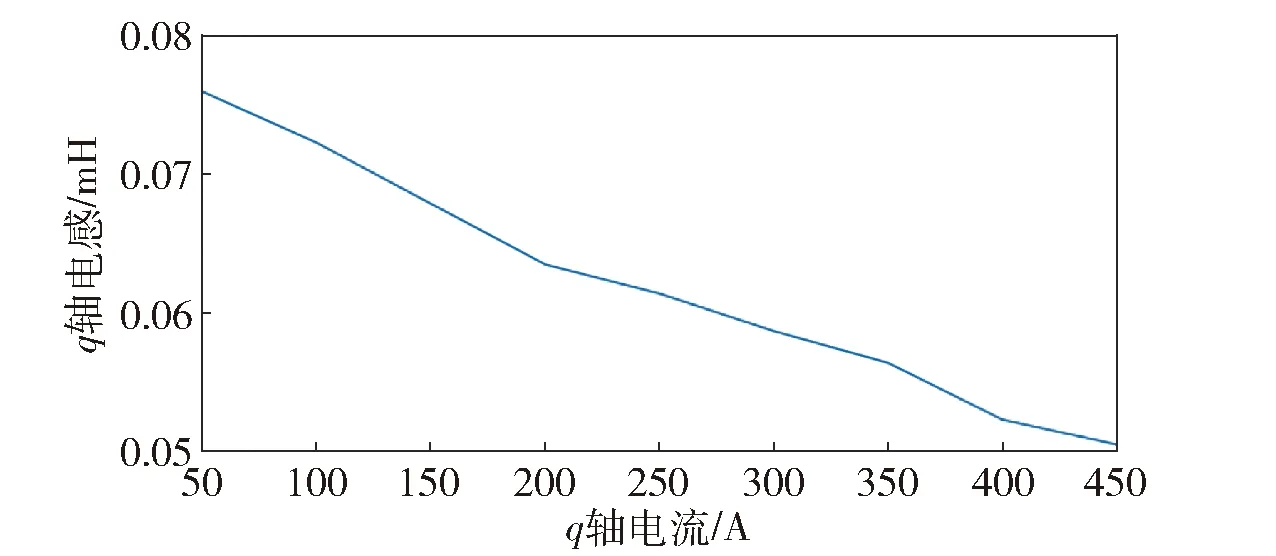
图13 q轴电感参数辨识结果

2 仿真及实验

实验平台为电机对拖系统，一台电机工作在转速环作为电力测功机，模拟特种车辆发动机，被测电机工作在发电模式，负载侧接电阻/负载箱模拟车用负载，仿真与实验皆按照前文发电策略进行。发电机参数如下：极对数p=12，相电阻Rs=2.4 mΩ，磁链λm=0.055 wb，电感Ld=0.068 mH，Lq=0.076 mH，额定电流有效值250 A，额定转速1 200 r/min，额定功率30 kW。

2.1 仿真

基于Simulink模块搭建模型进行仿真，给定发电机斜坡转速输入，于0.625 s时间点处达到算法切换阈值500 r/min，0.15 s时间点处达到发电转速阈值1 200 r/min，给定325 V发电指令，在0.25 s及0.8 s时间点处负载侧由开路状态依次切入10 kW、30 kW负载。

1.3节中提到，在工作区4内由于电机模型参数失配所导致的无位置算法角度观测误差将影响发电机带载能力，基于此进行参数失配下的仿真验证，将Simulink中的发电机q轴电感参数依照1.3节中离线辨识参数结果设置为随电流时变，而无位置算法中的电感参数保持默认常值，全工作区内仿真结果如图14所示。可以看到随着负载增加，电流增大，转速观测值出现大幅振荡，电压环无法正常跟随发电指令，电流环失控，验证了参数失配对于无位置算法的负面影响及参数辨识算法的必要性。

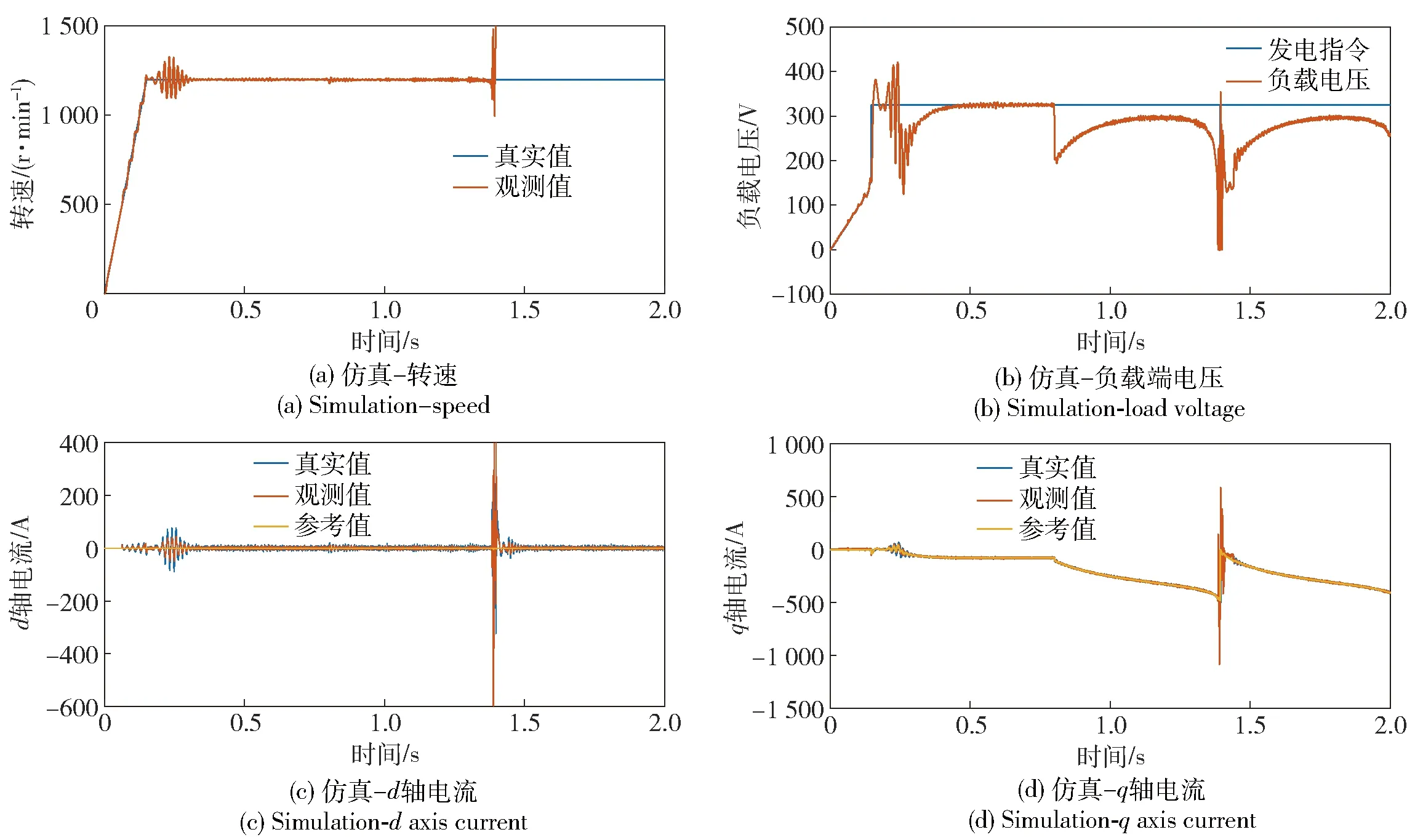
图14 参数失配下的仿真结果

结合1.3节中参数辨识结果实时向状态观测器更新电感参数，仿真数据如图15所示。图15(a)为发电机转速观测数据，可以看到无位置算法对于转速观测结果整体较为准确，在500 r/min处进行算法切换时，观测转速值有一个短暂的动态收敛过程，进入稳态后观测波动区间(-5 r/min,5 r/min)，在加载瞬间未出现明显波动；图15(b)为发电数据，在算法切换时，端电压未见明显波动，达到发电转速时，端电压能够实现稳定跟踪，在满功率负载处端电压波动区间(-5 V,5 V)；图15(c)～15(e)分别是发电机dq轴反电势及电流值，可以看到在整个工作区域内，基于无位置算法的电机控制算法在切换点处过渡平滑，保持了较好的电流控制精度，控制策略下，满功率30 kW 时，d轴电流波动区间(-20 A,20 A)，q轴电流波动区间(-20 A,20 A)。整个工作区域内转子位置最大观测误差12°，稳态误差6°，验证了该控制策略的可行性。

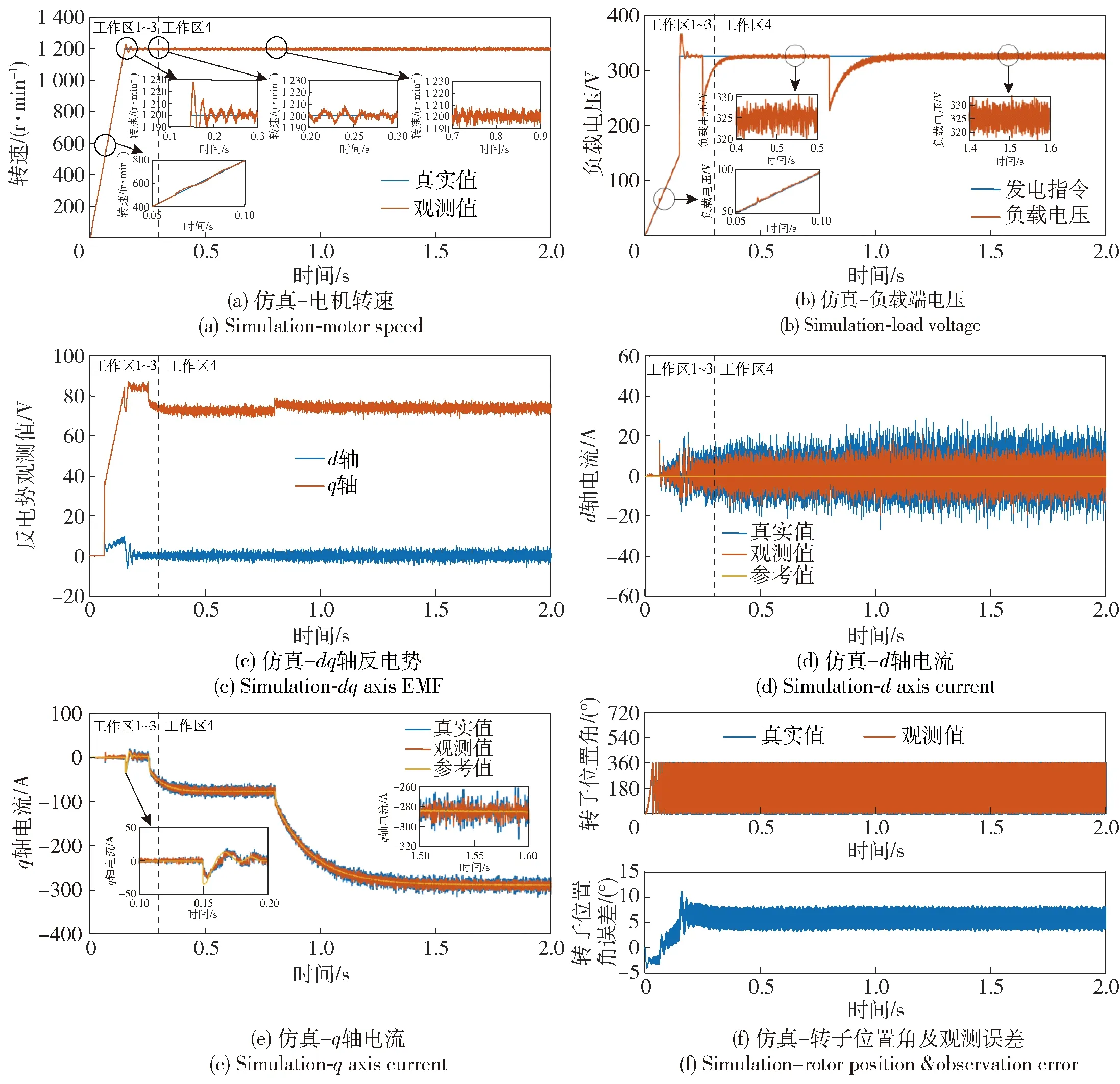
图15 全工作区仿真数据

2.2 实验

为进一步验证上述控制策略的可行性，进行了相应的实验验证，实验所用电机对拖平台、电阻负载箱及电机控制器如图16所示，控制器的数字处理芯片采用美国TI公司生产的TMS320F28335，同时选用AD2S1210硬件解码芯片获取电机实际转子位置信息与无位置算法进行对比。

图16 电机对拖实验平台

首先在未结合递推最小二乘算法的参数失配工况下进行实验，为保证实验安全，由电力测功机拖动发电机到达额定转速(1 200 r/min)，切入负载后采用升压方式测试系统带载能力，升压实验波形如图17所示，分别是参数失配下的观测电机转速、负载端电压及dq轴电流数据，可以看到当发电指令由210 V提升至215 V时，无位置算法观测转速发散，电压环无法完成指令跟踪，电流环失控，触发系统过流保护，停止工作。

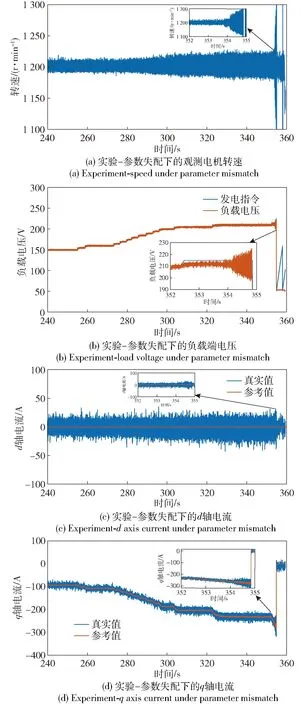
图17 参数失配下的实验数据

结合参数辨识算法，实时更新不同工况点的q轴电感参数进行实验，工作区1～3阶段的实验数据如图18所示，发电机0～1 200 r/min升速，当到达第2阶段转速阈值(500 r/min)时，切换到基于线性状态观测器的无位置传感器算法提供转子位置信息，当到达第3阶段转速阈值(1 200 r/min)时，电压环给定325 V发电指令。由实验波形可以看到在工作区切换时，观测转速及反电势过渡平滑，负载电压能够快速、稳定地跟随发电指令，dq轴电流未出现明显脉动，电机运行状态稳定。

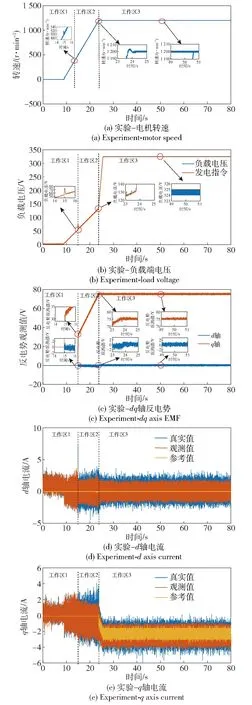
图18 工作区1～3实验数据

工作区4内进行负载投切，依次加载至满功率30 kW，再卸载至0 kW。实验数据如图19～图20所示。由图19a转速数据可以看到当负载发生变化时，无位置算法能较好地对转速进行跟踪，切入负载及切出负载瞬间，受电流波动影响，转速观测最大误差(-15 r/min,15 r/min)，进入稳态后转速误差波动区间(-2 r/min,1 r/min)；由图19(b)～19(d)电压及电流数据可以看到，控制算法电压环、电流环响应快速稳定；由图20实验数据可以看到，进入稳态后转子位置观测误差4°，相电流波形平稳，验证了算法的可靠性与稳定性。

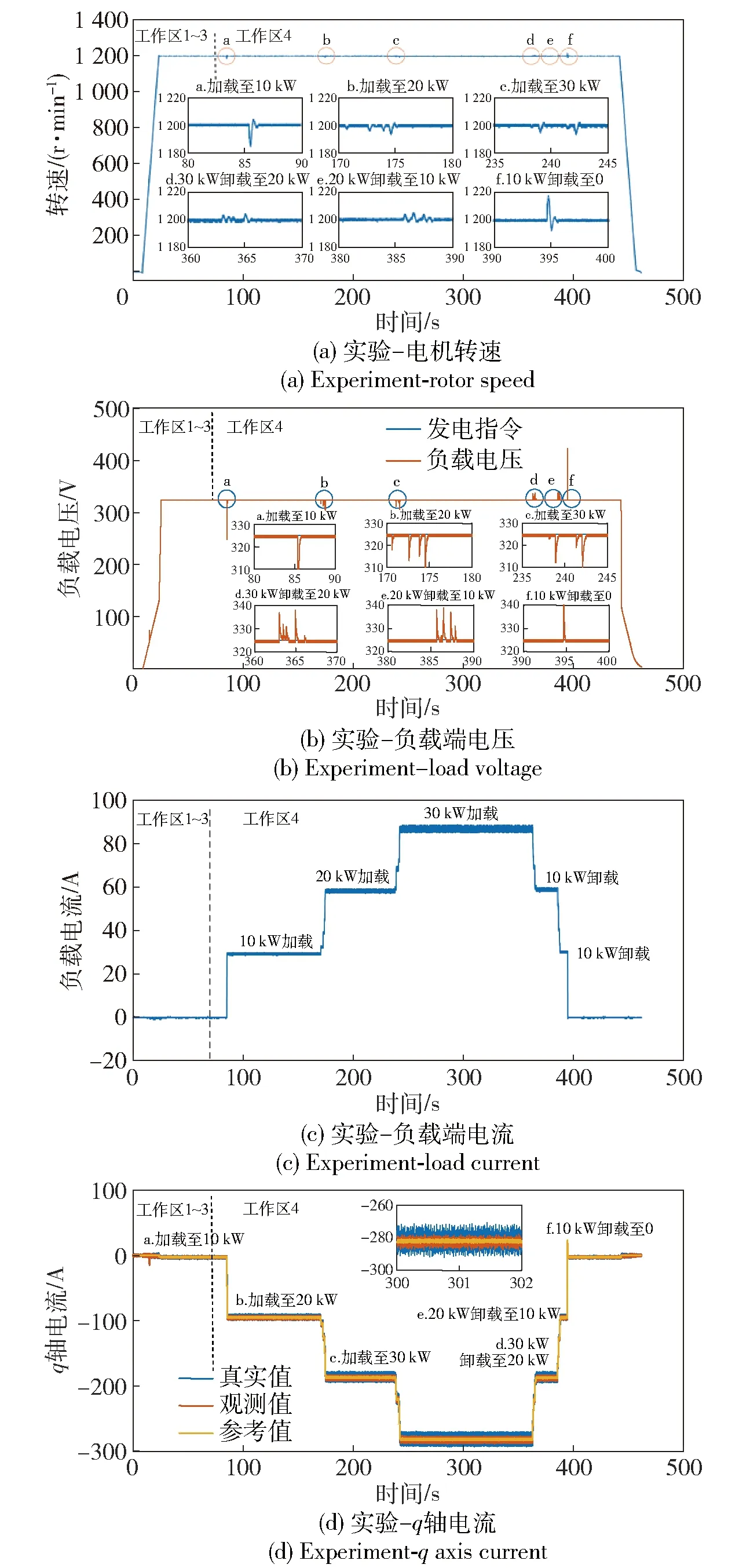
图19 工作区1～4实验数据

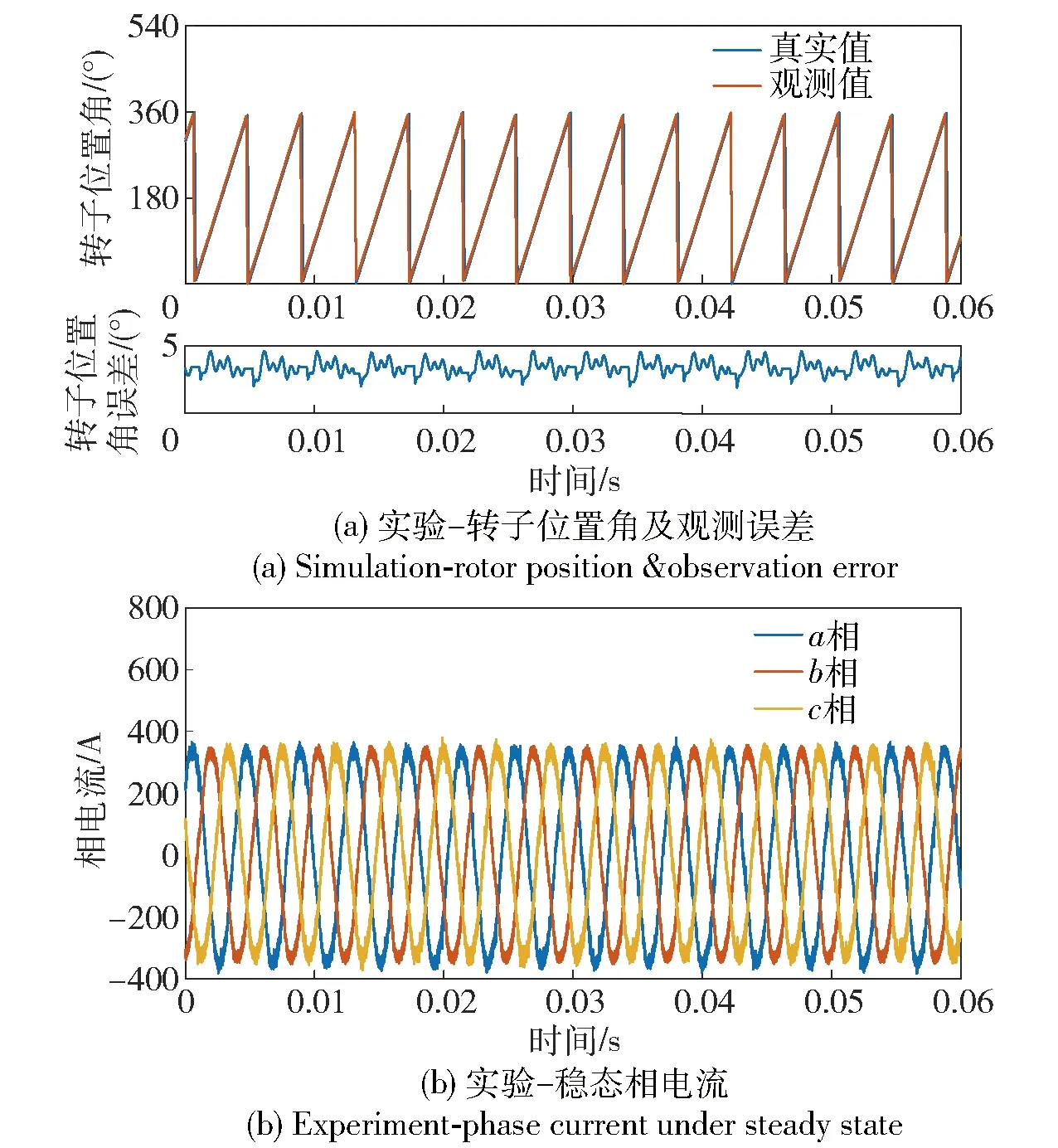
图20 30 kW稳态实验数据

3 结论

本文研究了一种全电化军用特种车用全速度范围内的永磁同步发电机无位置传感器控制策略，整个控制过程分为4个工作区，在工作区1内，采集三相电压，通过基于正交锁相环的角度跟踪器获取转子位置信息；在工作区2内，切换到基于线性状态观测器的无位置算法，结合递推最小二乘算法，离线辨识出不同电流工况下的q轴电感，以在线查表的方式实时更新状态观测器参数；在工作区3～4内完成系统发电目标及负载投切。在低速工作区内，相较于传统的高频信号注入法，本文提出的控制策略对电机凸极性无强制要求，不产生额外的涡流损耗，硬件电路实现简单；在中高速区内，结合递推最小二乘算法消除了不同工况点参数时变的影响，保证了发电系统在大功率工况下的带载能力，鲁棒性强，实现了特种车辆发电系统在全速域、全工况范围内的稳定控制。

本文阐述了基于正交锁相环的角度跟踪器工作原理，分析了系统的动、静态特性与调节器系数之间的关系。建立了在估算坐标系下的电机状态空间方程，给出了反馈增益矩阵的求解思路，并基于李雅普诺夫第二法对观测器稳定性进行了分析。基于对拖实验平台对上述控制策略进行验证，发电机最大输出功率30 kW，实验结果验证了本文所提控制策略的正确性和有效性。