一种面向非线性材料的二维高阶ANCF 梁单元

郭嘉辉，赵春花，独亚平，周川

（201620 上海市 上海工程技术大学 机械与汽车工程学院）

0 引言

随着科学技术的发展，机械系统中出现了柔性可变形构件。构件在运动过程中不仅存在刚性运动，也发生了弹性变形，其影响不可忽视。人们创建KED 法、浮动坐标法以及绝对节点坐标法解决这类柔性多体系统动力学问题。绝对节点坐标法[1]将单元节点定义在全局坐标系下，利用梯度向量作为旋转坐标，因此具有常数质量矩阵以及不存在科氏力和离心力项。此外，运用连续介质力学理论不仅可以建立线弹性力矩阵，还可以方便地引入非线性弹性模型建立非线性弹性力矩阵。因此相比其它方法，它可以更方便地建立系统的非线性运动微分方程，在描述系统运动过程中的大转动大变形情况比其它方法更具有优势。多年以来，绝对节点坐标法因此而受到广泛关注和研究。人们基于这种方法开发了梁、板、壳以及实体单元。

尽管如此，人们通过绝对节点坐标法建立的单元也存在着一些问题，本文主要研究的是含非线性弹性力作用下的二维ANCF 剪切梁单元的单元性能。有关研究中，Maqueda[2]等人在三维ANCF 梁单元中建立了Mooney-Rivlin 和Neo-Hookean 弹性力模型；Jung[3]等人通过橡胶单摆运动实验观察比较了三维ANCF 梁单元在3 种超弹性本构弹性力模型下的仿真结果；Orzechowski[4]通过选择性简约积分法以及罚函数方法缓解了低阶三维梁单元的闭锁问题；Xu[5]等人通过实验和仿真分析了由Shen[6]提出的42 节点高阶单元能够解决非线性本构方程带来的单元闭锁问题。此外，Xu[7]还在ANCF 梁单元建立了Arruda-Boyce 非线性弹性力模型。

本文利用基于Yeoh 模型建立二维梁单元的非线性弹性模型，对二维ANCF 梁单元进行深入研究，在此基础上提出了一种面向非线性弹性材料的二维高阶梁单元，利用大变形深梁静力学算例以及悬臂梁运动学算例验证模型性的有效性，并通过与ABAQUS 软件的仿真情况和不同二维高阶ANCF 单元进行比较分析，讨论了单元的精度问题。

1 单元模型：二维高阶ANCF 剪切梁单元

Zhao[8]等人在剪切梁单元[9]的位移模式中引入了y2项。本文通过对位移模式的深入研究，进一步将x2y 项引入位移模式中，建立新的绝对节点坐标法梁单元（B-2n）位移模式。在全局坐标系下定义的二维单元位移矢量ri表示单元内任意一点的位置矢量（ri1，ri2），其中ri1和ri2可用全局坐标x、y 的多项式表示。另外，位移模式ri也可以表示成节点广义坐标e 和相应的形函数S，表达式为：

2 基于Yeoh 非线性弹性模型下的弹性力及运动方程的推导

Yeoh 模型[10]为橡胶材料的常用本构模型之一，其物理特性可由应变能密度函数W 表示：

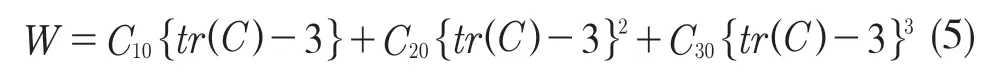
式中：C10，C20，C30——材料系数。C——右Cauchy-Green 变形张量，C=JTJ；J——位置梯度矩阵；tr（C）——矩阵C的迹。

此外，橡胶材料被认为具有体积近似不可压缩特性。文献[2] 指出可利用罚函数对应变能方程密度函数进行修改，以确保材料的不可压缩性。其中，α取值越大越有利于保证材料的不可压缩性。不可压缩Yeoh模型的总应变能密度函数为：

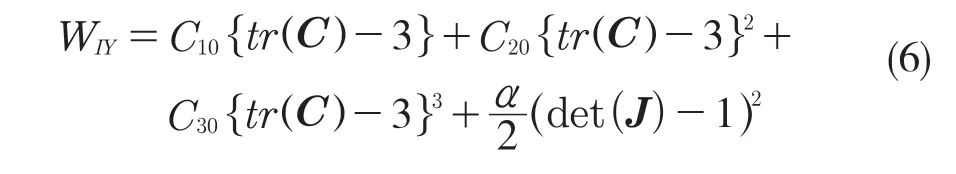
对式（6）求积分，可得不可压缩Yeoh 模型的总应变能

接下来，根据拉格朗日方程推导运动方程。

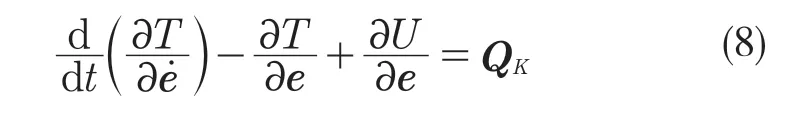
式中：T——单元动能；U——单元应变能；QK——广义外力矢量阵；t ——时间；——节点广义坐标e 对时间t 的导数向量。

根据式（7），可以推出单元弹性力QT为：

另外，单元动能依据定义推导，如式（10）：

式中：ρ——单元材料密度；V——单元体积；M——单元质量矩阵；——节点坐标e 的向量的时间导数。根据式（10），可提取单元的质量矩阵为

则单元运动微分方程表示如下：

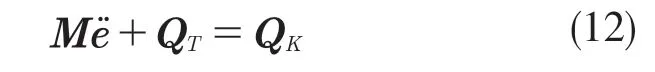
3 数值算例

3.1 静力学算例：大变形深梁模型

本节采用的深梁模型如图1 所示。由于深梁横截面有较大变形，使得单元闭锁情况加大，便于检测单元受到较大变形时的静力学计算[11]。深梁物理参数：长L=2 m，宽W=0.1 m，高H=0.5 m；不可压缩Yeoh 本构模型的材料系数分别为C10=0.545 235 MPa，C20=0.061 049 8 MPa，C30=-0.000 802.537 MPa；罚函数U 的系数α=1 000 MPa。深梁的端部末端受到集中力为F=-1 000 N。本算例中使用的参考解为有限元软件ABAQUS 计算的收敛解。在表1 中显示了深梁端部位移的计算结果。

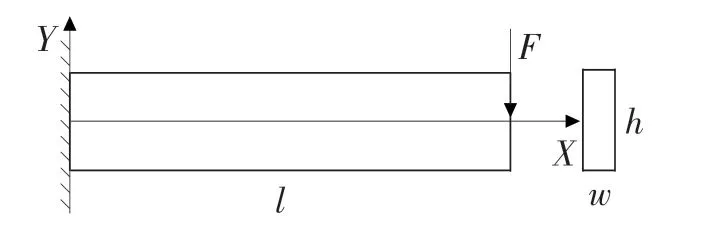
图1 深梁模型Fig.1 Deep beam model

从表1 中可以看出，随着单元数的增加，本文所建立的单元B-2n 的计算结果收敛，表明该单元模型的是有效的。与单元2D2N[8]计算结果相比较，模型B-2n 的计算结果与ABAQUS 的仿真结果更接近，说明加入x2y 项使得单元精度变得更高了。

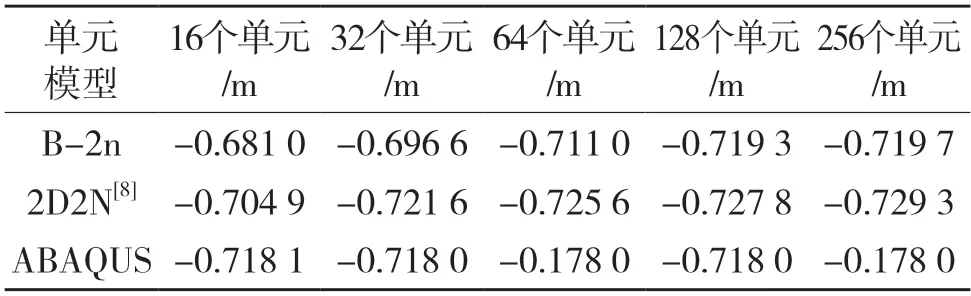
表1 深梁端部在Y 方向位移比较Tab.1 End displacement comparison of deep beam in Y direction

3.2 动力学算例：受重力作用悬臂梁模型

利用受重力作用的悬臂梁模型分析单元闭锁问题对单元动力学特性的影响。如图2所示，悬臂梁物理参数：长L=1 m，宽W=0.1 m，高H=0.1 m；不可压缩Yeoh本构模型材料系数：C10=0.545 235 MPa，C20=0.061 049 8 MPa，C30=-0.000 802 537 MPa；罚函数Up的系数α取1 000 MPa。摆的初始状态是水平的，其初始速度为0，重力加速度为g=9.81 m/s2。在重力的作用下悬臂梁在XY 平面内从右侧往下摆动至最左端，整个仿真时间为0.6 s。

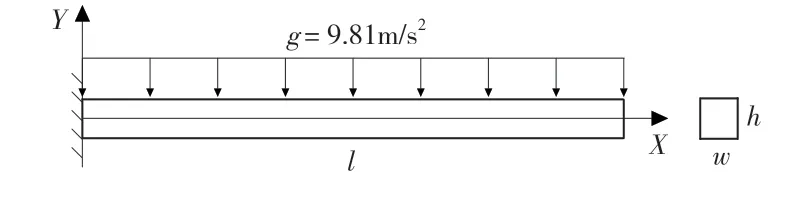
图2 重力作用下的悬臂梁摆动模型Fig.2 Swing model of cantilever beam under gravity

图3 是在不同单元数下，利用本文的ANCF 高阶梁单元B-2n 对悬臂梁末端点的位移计算结果。

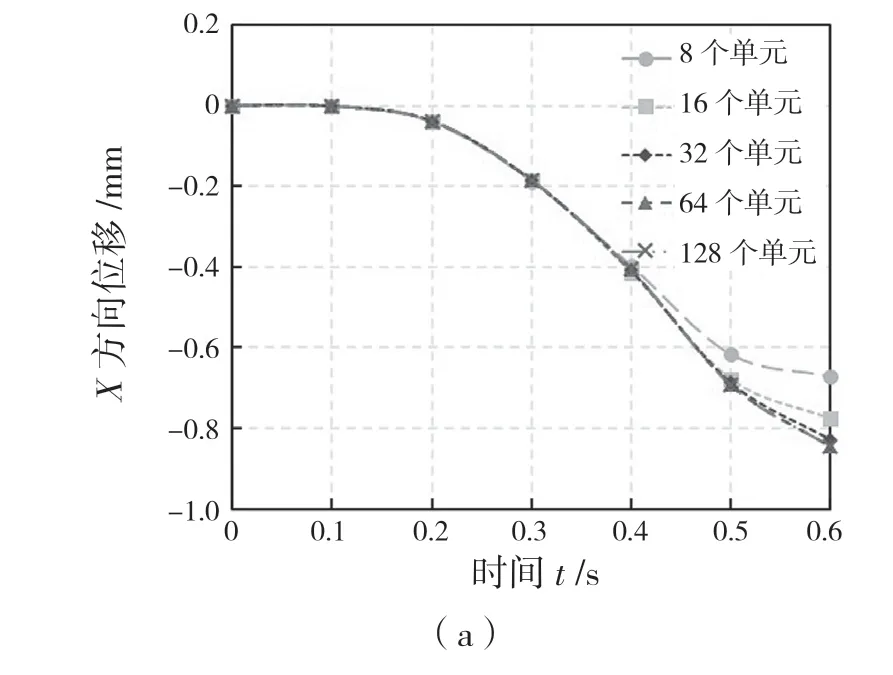
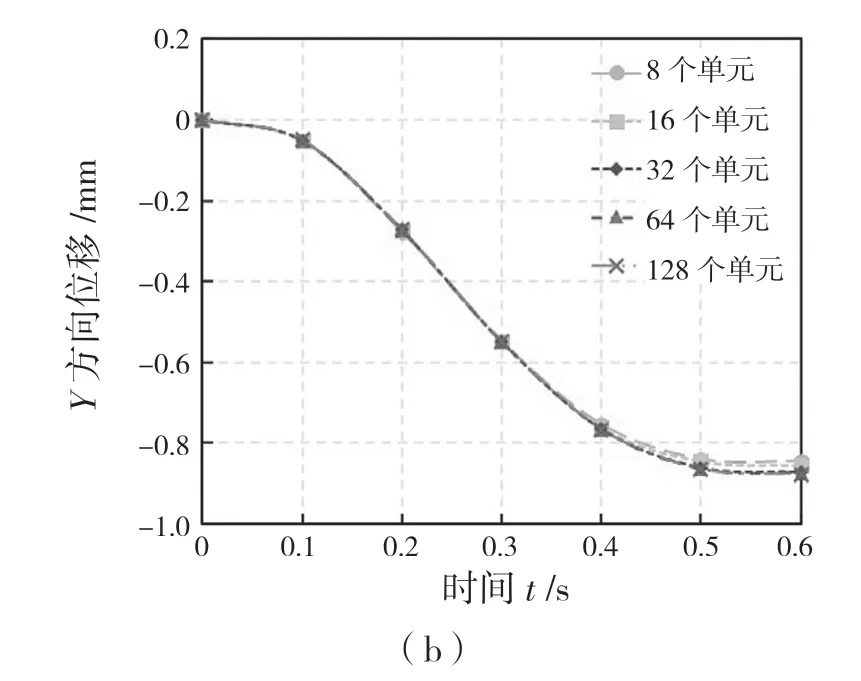
图3 单元收敛性分析Fig.3 Convergence analysis of the element

由图3 见，随着单元数的增加，单元计算结果是收敛的。当单元数到达32 时，模型已经开始收敛，图中64 个单元结果与128 个单元结果一致。因此，采用64 个单元数下的计算结果作为收敛结果分别与ANCF 高阶单元2D2N[8]和有限元软件ABAQUS的仿真结果进行比较，其结果如图4 所示。

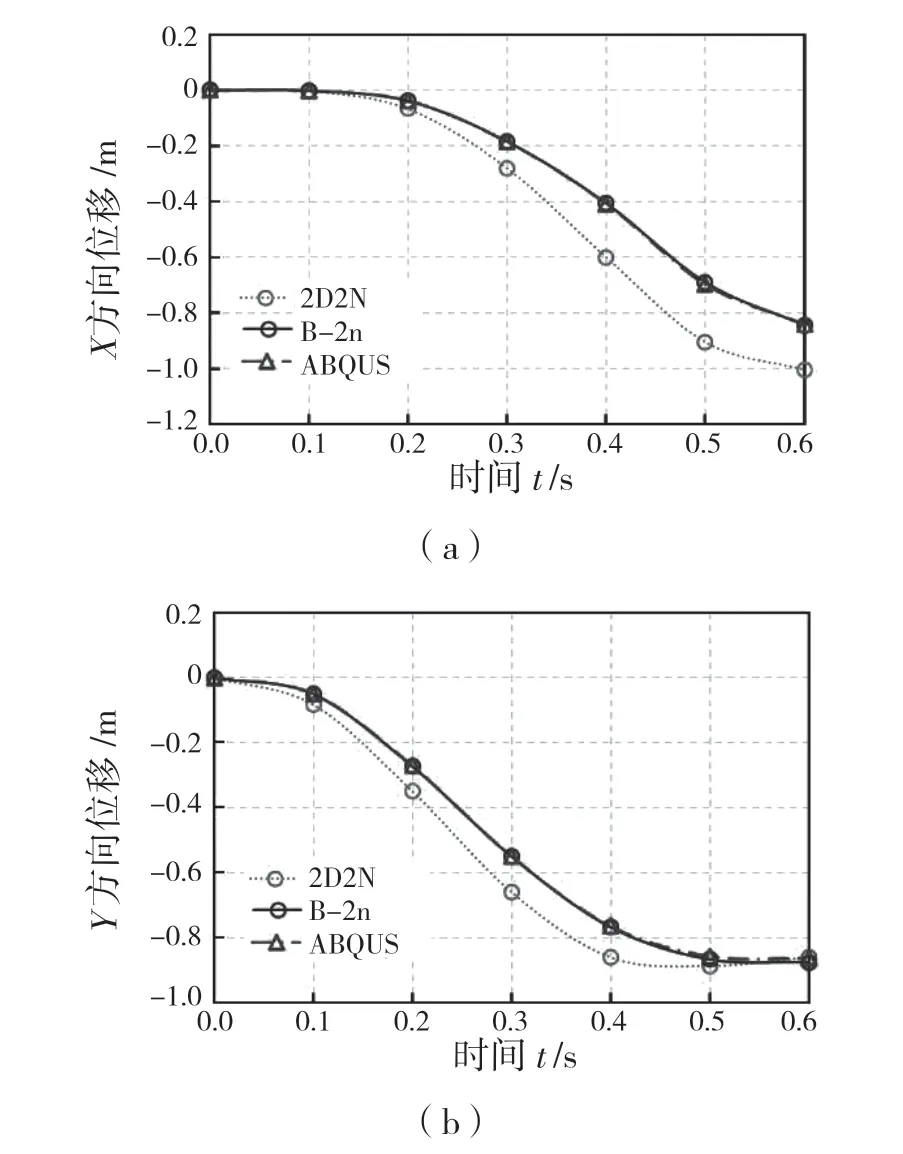
图4 不同单元下的悬臂梁端部位移分析比较Fig.4 End displacement comparison of cantilever beam using different elements

从图4 可以看出，本文提出的单元计算结果与ABAQUS 仿真结果趋于一致，而2D2N[8]模型计算的结果也接近ABAQUS 仿真结果。两者相比较，本文提出的单元可以更有效地模拟非线性弹性下的悬臂梁大变形运动过程。

4 结论

本文构建了一个2 节点二维高阶ANCF 剪切梁单元，通过静态以及动态算例分析，并将得到的结果与ABAQUS 软件中仿真结果进行比较、分析，得出结论：（1）在静力学中，本文提出的梁单元模型能够有效地分析深梁模型的大变形，单元模型的收敛精度较高；（2）在动力学分析中，本文提出的单元显示了良好的计算精度，适用于大变形非线性材料问题中的动力学研究与分析。