新趋近律的直流微电网母线电压滑模控制设计

苗 真，张 雷

(河南科技大学 电气工程学院，河南 洛阳 471023)

0 引言

太阳能发电、水力发电、风力发电以及电动汽车等过多分布式电源的直接并网会对电网的稳定性乃至系统的正常供电造成重大冲击，严重时甚至会造成人身事故。所以，迫切地需要解决分布式电源并网消纳的问题。微电网作为未来分布式能源系统的主要发展趋势之一，对推进节能减排、实现能源的可持续发展有重要意义[1-4]。现阶段，负荷类型多种多样，分布式电源的装机容量也越来越大，直流微电网凭借其可控性、经济性以及在供电质量上的优越性能，逐渐得到国内外学术界的广泛关注。

新能源的发展为解决能源危机和环境保护问题提供了捷径，将众多分布式电源以微电网的形式接入大电网是个行之有效的办法。微电网将分布式电源、储能装置和负荷等组成部分综合在一起，形成一个小型发配电系统。对微电网内来说，它可以完成微电网的自行调控和保护自治的功能；对微电网以外来说，它能简化成单一的受控源，最大优势是可以一直保持独立运行的能力。

发展微电网有以下几点原因：(1)微电网的加入可以满足电网对分布式电源的需求，微电网是连接分布式电源和大电网之间的桥梁；(2)可以通过它将电能传送到电资源紧张和稀缺的地区；(3)因为它良好的稳定性，即便电网发生了故障，也能及时恢复供电。

如图1所示，直流微电网通过直流母线将分布式电源、储能单元和负荷等连接起来，构成一个独立于大电网之外且可以单独运行的发电系统。其主要的优势如下：

1)损耗小，效率高；

2)电力变换装置少；

3)节约输电走廊；

4)可以实现自我管理，运行和维护系统的可靠性比较高；

5)直流微电网可以在并网模式与孤岛模式之间实现无缝切换，不仅可以向外部负荷提供电能，而且在外部网络故障的情况下也可以直接向用电设备供给电力。

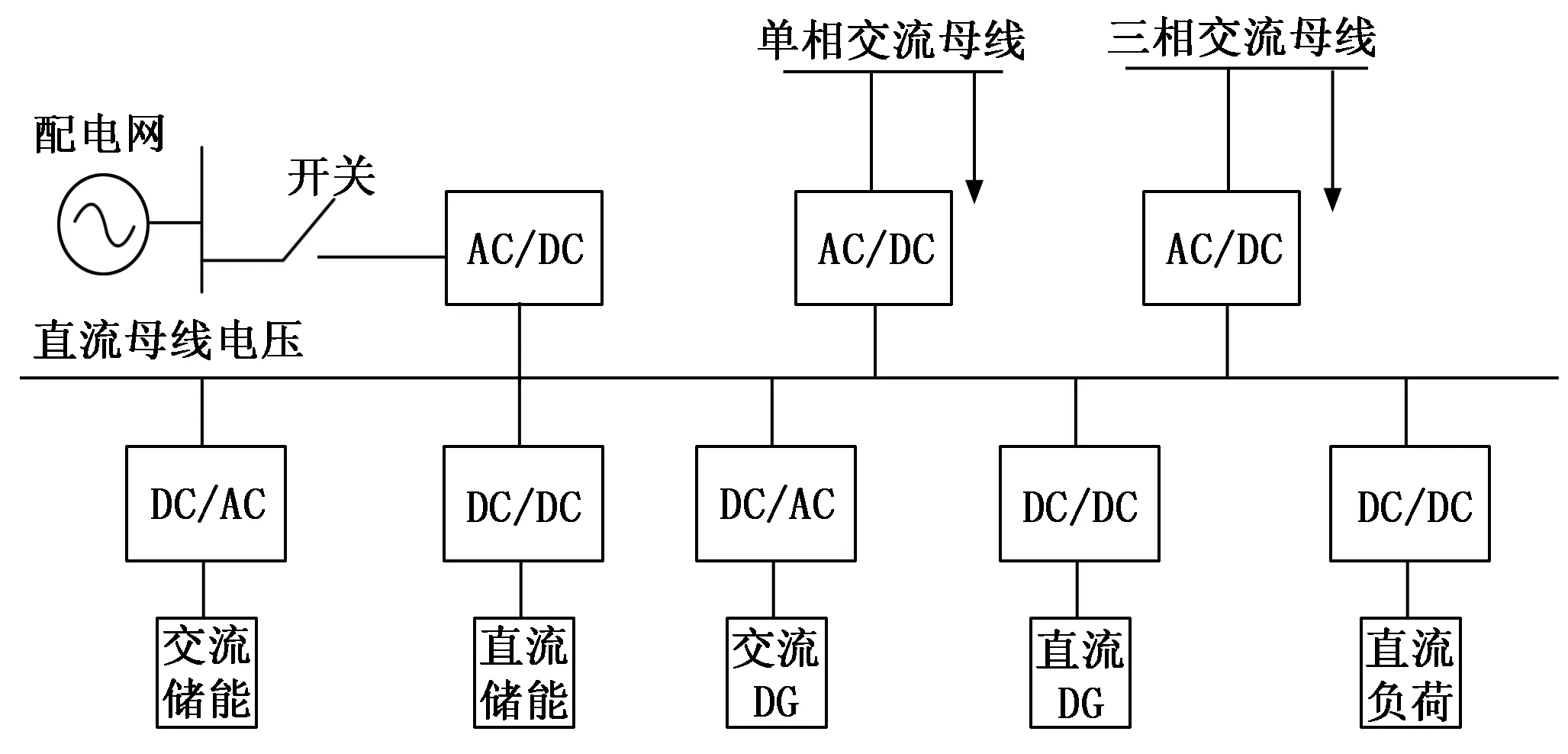
图1 直流微电网结构图

直流微电网存在以上众多优点，但它也极易受自身或外界扰动的影响。比如，由于光伏或风电输出功率的不稳定，而导致输出电压不稳定的问题；由于自身的非线性负载的变动而出现的波动问题；供电可靠性和损耗问题等等。这些问题都会严重影响直流母线电压的稳定，造成分布式电源的波动，严重时会导致直流母线电压的保护动作，影响正常供电。直流微电网母线电压控制系统是一个集非线性和强耦合于一身的系统，该系统往往也会出现复杂电力系统的通病，比如：微电网输出功率不够稳定，从而导致输出电压出现不稳定的问题；并且由于自身的非线性负载的变动而可能出现的母线电压波动问题；供电可靠性和损耗问题等等。综上所述，直流微电网的母线电压的稳定控制是直流微电网正常高效持续运行的关键所在[5-9]。所以，本文意在通过应用设计高效的控制器的方法，让直流微电网中存在的缺陷降到最低，实现其合理使用。

传统的PI控制因其算法简单在直流微电网母线电压内外环控制中均得到了充分的利用。但PI控制方法在实际系统中，容易受到参数摄动与负荷扰动的负面影响，不能得到理想的控制效果。滑模控制作为典型非线性控制方法凭借其不依赖被控对象模型、鲁棒性好等特点被普遍应用于直流微电网母线电压控制系统中，例如：文献[10]利用自适应滑模控制的直流微电网稳定策略，开发了一种微电网稳定控制器，保证了微电网在并网、孤岛和切换模式下的稳态及动态特性。文献[11]针对光储微网系统的抖振问题，引入新的组合函数代替幂次函数，设计了一种新型滑模控制器，提高了防抖振性能。

在直流微电网母线电压的控制系统中，直流微电网中电源输出的功率或者负荷的突变等扰动均会对直流母线电压造成较大的冲击[12-13]。因此，设计一种高性能的扰动观测器尤为关键，它能够有效的观测系统出现的扰动，扰动估计值也能通过前馈的方式补偿到控制器的输入中[14]，进而提高直流母线控制系统抑制母线电压扰动的能力。例如，文献[15]提出了一种干扰观测器，在不需要额外传感器时也能实现对系统扰动的快速跟踪。文献[16]直流微电网系统中非线性及参数变化对母线电压稳定的影响，将扩张扰动观测器与Backstepping相结合，补偿了系统的非线性和参数的变化，提高了系统的抗扰动性能。文献[17]设计了一种基于鲁棒扰动观测器的动态补偿法，能够在不改变参数的情况下，提升动态性能，抑制负载、功率波动以及交流侧负载不平衡等引起的直流母线电压波动，增强系统的鲁棒性。

抖振现象是滑模控制器固有属性之一，抖振可能激发被控系统中的高频未建模动态[18-20]，对系统的性能有较大的损害。而可以通过设计一种恰当的趋近律来改善滑模控制器的趋近速度和抖振现象的矛盾[21]。本文针对直流母线电压控制系统的滑模控制器模型，设计了一种新型趋近律。当系统的轨迹距离滑模切换面比较远时，恰当的趋近律使得运动点趋近滑模面的速度增大，来降低趋近时间；当系统的轨迹接近滑模面时，其速度趋近于零，以减小系统抖振[22]。同时，为了抑制直流母线电压控制系统可能出现的外部扰动，设计了扩张状态观测器观测系统扰动，观测器将观测到的扰动值补偿至滑模控制器中，能够进一步提高复合控制器的抗扰动能力，保证直流微电网系统的稳定性和鲁棒性。

1 三相AC/DC变换器数学建模

三相全桥逆变器具有结构简单控制、方法易于实现等特点，在直流微电网母线电压控制系统中应用最为广泛。图2为三相全控并网AC/DC变换器拓扑结构，其组成包括直流电源Udc、逆变器侧电感L、线路负载电阻R、三相电网和滤波电容C，S代表变流器的桥臂的通断信号。

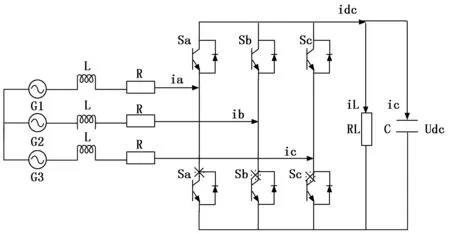
图2 三相变换器电路拓扑图

为得到更简洁的三相AC/DC变流器的数学模型，可作如下假设：

1)交流侧的电源可被看作是无穷大电源；

2)交流系统可看作是三相对称的系统；

3)功率开关管是理想器件模型。

由图2可得，三相静止坐标系下的数学模型为：

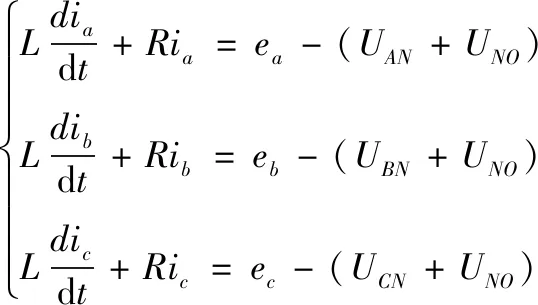
(1)

UAN、UBN和UCN分别为abc三相的电压，它们与直流电压Udc和3个上开关函数Sa、Sb和Sc有关，关系如下式所示：

(2)

假设交流侧的三相系统平衡，则可得：

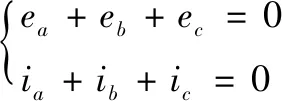
(3)

联立上式可得：

(4)

列写基尔霍夫电流方程，可得：

(5)

对于直流微电网双向AC/DC变换器，任意时刻都会有3个功率开关管是处于开启状态，直流微电网母线电流可表述为：

(6)

整理可得：

idc=iaSa+ibSb+icSc-iL

(7)

联立可得：

(8)

由电路拓扑图及所做出的假设，可通过基尔霍夫定律得到三相AC/DC双向变流器在三相静止坐标系下的数学模型为：

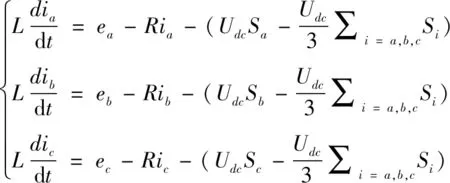
(9)

(10)

三相静止坐标系下的数学模型变量间存在着较强的耦合关系，这不利于控制器的设计。所以，需要对数学模型进行解耦处理，从而简化控制器的设计。

将三相静止坐标系下的直流微电网双向AC/DC变换器的数学模型通过变换，转化到两相静止坐标系下，可得下式：

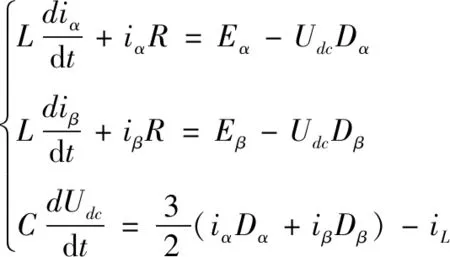
(11)

式中，E为电网电压在上的分量；iα和iβ为电流；Dα和Dβ为占空比函数；iL为流过负载两端的电流。坐标变换方便地解决了变量之间的耦合问题。

Xe=Xe-jθ

(12)

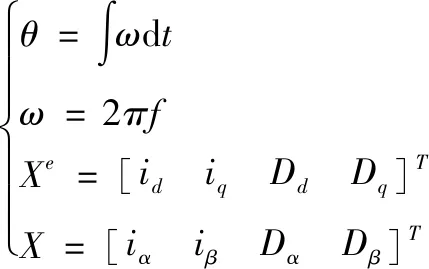
(13)

式中，Xe为两相旋转坐标系下的状态变量；X为两相静止坐标系下的状态变量；θ为q与α轴的夹角；ω为旋转角的速度，其中f=50 Hz，则ω=314 rad/s。

两相静止坐标系变换至两相旋转坐标系的变换矩阵为：

(14)

数学模型经过上式的变换矩阵坐标变换后，可以得到在两相旋转坐标系下的数学模型为：

C2s/2rTabc/αβZX=C2s/2rTabc/αβAX+C2s/2rTabc/αβU

(15)

最后，经过两种坐标变换后，得到的变换器的数学模型为：

(16)

式中，ed和eq为电网电压在d轴和q轴上的分量，id和iq分别为d轴和q轴上的电流，Dd和Dq分别为d轴和q轴上的占空比函数，iL为流过负载的电流。本小节通过坐标变换将变换器的数学模型从三相静止坐标系变换至两相旋转坐标系，从而有利于之后控制器的设计。

2 直流微电网母线电压的PI控制策略

PI控制具有简单可靠易于实现的特点，常被应用于直流微电网母线电压的控制系统之中，本小节根据上一节中所建立的变换器的数学模型来进行相关控制器的设计。

2.1 电流内环PI控制器设计

良好的电流跟踪性能能够有效的提高母线电压控制效果，首先，需要进行电流内环控制器的设计。

两相旋转坐标系下变换器的数学模型为：

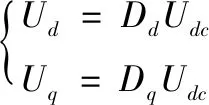
(17)

式中，Ud和Uq是电流内环d轴和q轴的控制变量。

联立可得：

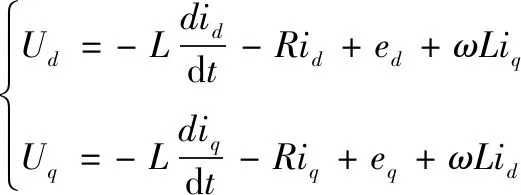
(18)

将上式进行拉普拉斯变换，可以得到在两相旋转坐标系下的直流微电网双向AC/DC变换器的频域模型为：

(19)

为了简化控制器的设计难度，通常可以采用前馈补偿的方法来来对内环控制系统进行解耦处理。将前馈变量-ωLIq(s)和ωLId(s)引入到双向AC/DC变换器的网侧电压矢量来抵消系统中存在的耦合项，从而实现dq坐标轴变量之间的解耦，前馈控制框图如图3所示。

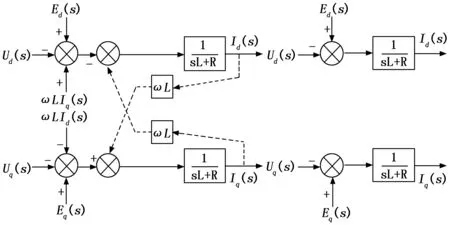
图3 前馈控制框图

引入的前馈变量-ωLIq(s)和ωLId(s)虽然可以解决dq轴状态变量之间的耦合关系，但是Id(s)仍会受到Ud(s)和Ed(s)的影响。因此，需继续引入状态变量-Ed(s)来抵消其影响。当直流微电网双向AC/DC变换器控制系统中的电流内环控制器采用PI控制器时，控制系统的输出为：

(20)

整理可得：

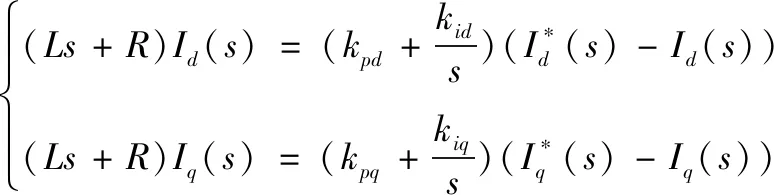
(21)

2.2 电压外环PI控制器设计

电压环控制是控制器的最外环，它会对直流微电网的母线电压进行直接的影响，所以外环控制器的性能也会直接决定最终母线电压的控制效果，下面将针对电压外环进行PI控制器设计。

由图2可知，直流微电网母线三相电动势为：

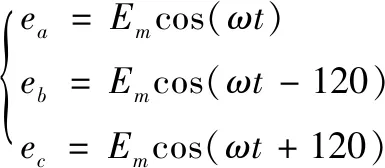
(22)

网侧电流可表述为：

(23)

忽略高频分量的影响，则Sk为：

(24)

式中，θ为开关函数导通时的初相角，m为脉宽函数调制比(m≤1)。

则直流微电网母线电流为：

idc=Saia+Sbib+Scic

(25)

推导可得：

idc=0.75mImcos(θ)

(26)

则直流微电网双向AC/DC变换器的电压外环传递函数为：

(27)

按照双闭环PI控制策略整定电压外环比例增益kup与积分增益kui，得：

(28)

由上式推导的结果可以得知，当滤波电容参数已知时，可以根据电容的大小进行电压外环的参数配置。但是随着时间的推移，电容会存在老化现象，其电容值会发生变化，这将影响PI控制器的控制效果，即PI控制器对系统参数变化较为敏感，当系统参数发生漂移，控制性能将会进一步恶化。而且由于PI控制器本身的结构，使得其存在超调与调节时间无法兼顾这一问题，且其抗扰动能力也是有限的。考虑到在直流微电网母线电压控制器中，外环往往决定了整个控制器的控制性能，所以为了克服上述问题，在下文将引出基于新型趋近律的直流微电网母线电压外环滑模控制器的设计，该控制器的设计可以有效地提高系统抗扰动的能力。

3 ESO-NRSMC的设计及稳定性分析

3.1 直流微电网母线电压控制器

在正常的工况下，内部参数摄动或负荷的扰动均可能扰乱直流微电网中直流母线电压的稳定，母线电压稳定性不足将会影响到微电网的正常供电。控制原理图如图4所示，常用的母线电压控制方式为采用两个电流内环和一个电压外环的来对母线电压进行控制。电流内环跟踪电压外环输出的给定值，而电压外环控制器起到维持母线电压稳定的作用，其性能决定了整个系统的控制性能。而本小节中直流母线电压的电压外环通过所设计的基于扩张扰动观测器的新趋近律滑模复合控制器ESO-NRSMC(extend state observer-New reaching law sliding mode control)进行控制。

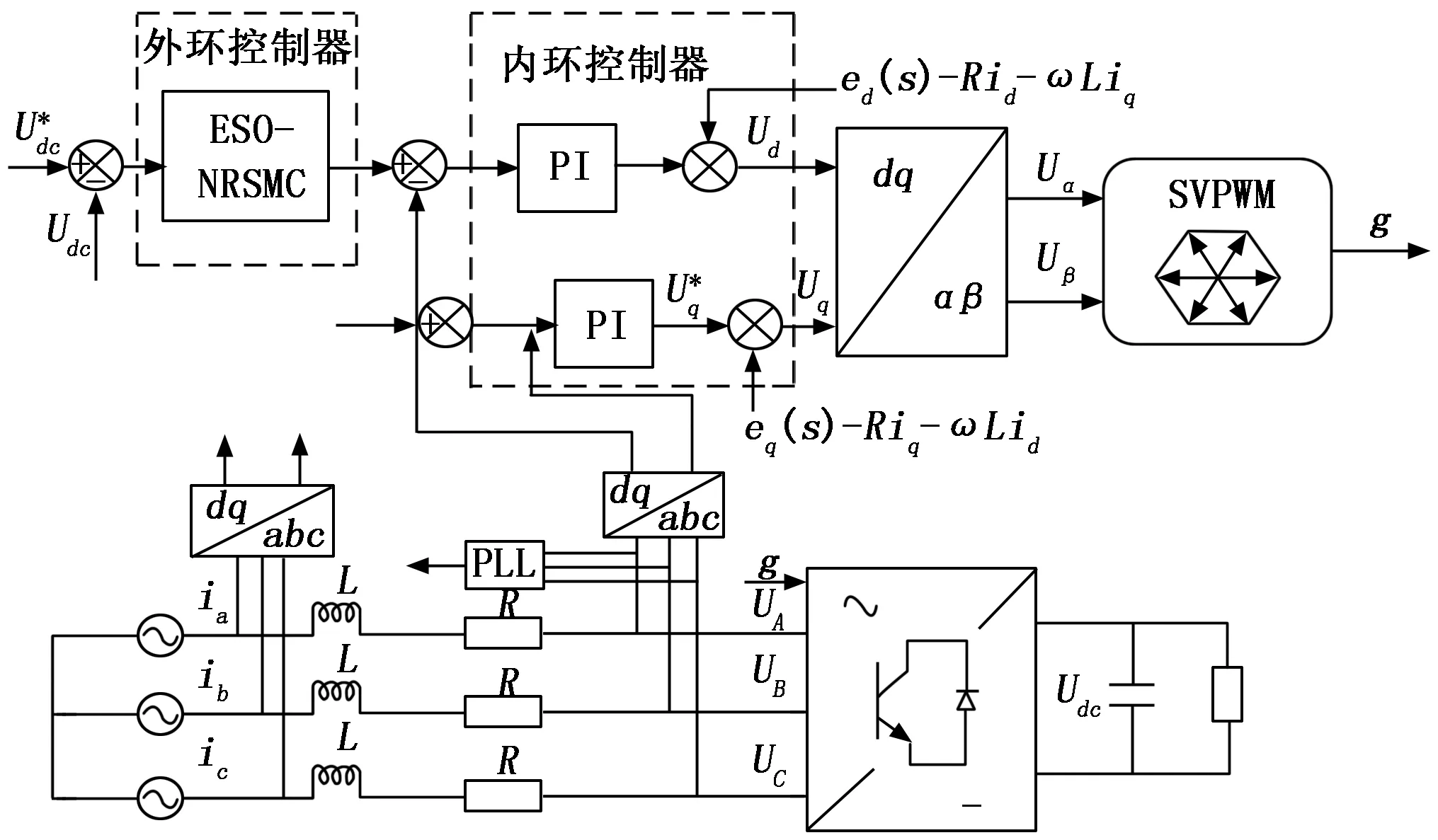
图4 直流母线电压控制原理图

3.2 新型趋近律的设计

设计滑模控制器的步骤一般包含选择恰当的滑模面和设计趋近律，从而让系统的轨迹能在控制律的作用下逼近滑模面。传统的指数趋近律如下式：

(29)

其中:s为滑模面，ε与k为大于零的常数。指数趋近律有自身的缺点，在指数趋近律的作用下，系统向原点进行运动时，并不能逼近原点，而是在其附近产生高频抖振。而新设计的滑模趋近律由变速趋近项和终端吸引趋近项构成，在变速趋近项中引入反正切函数，当滑模函数远离滑模面时，变速趋近项较大，加速收敛过程；当滑模函数接近滑模面时，变速趋近项较小抑制高频抖振。终端吸引趋近项相较于传统的指数趋近项提高了收敛速度，能在有限时间内收敛至滑模面，提升了滑模控制器的瞬时性。

(30)

式中,ε>0，k>0，ε的具体表达形式为下式：

(31)

综上分析表明：采用这种新型趋近律可以维持系统在接近或远离滑动模态时都具有很好的趋近性能，并且也可以抑制抖振现象，具有时间可达性。

3.3 基于扩张状态观测器的滑模控制器

针对于母线电压外环控制系统可能受到外部扰动的影响，本文引入了扩张状态观测器来观测系统可能受到的负载扰动，首先可将外环母线电压模型写为下式：

(32)

式中,dt为总的扰动值，定义系统的两个状态变量值X=[x1,x2]=[Udc,dt]，根据设置的状态变量得到新的状态空间表达式为：

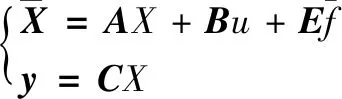
(33)

其中：

(34)

为了观测扰动值，设计以下的线性扩张状态观测器：

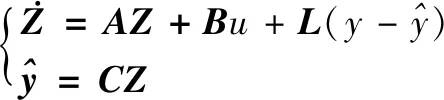
(35)

式中，Z=[z1,z2]T为扩张状态观测器的输出值，z2是扰动量的估计值，L=[β1,β2]T是观测器的增益参数。

图5为ESO-NRSMC控制器结构图，扩张状态观测器将观测到的扰动值对滑模控制器进行前馈的补偿，实现对系统可能出现的扰动的有效抑制。最终由滑模控制器得到外环电压控制器输出，即d轴参考电流值。

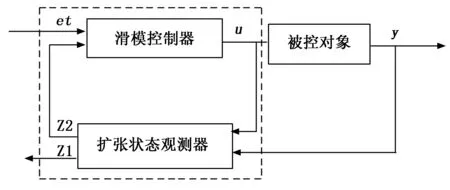
图5 ESO-NRSMC控制器结构图

下面将设计基于扩张扰动观测器的滑模控制器。首先定义母线电压跟踪误差为：

(36)

以母线电压误差为自变量，选取积分型滑模面为：

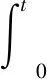
(37)

积分滑模面可以平滑控制器输入，并且让控制律中不会出现变量的二阶导数，可以增强控制器的稳定性。

最后，电压外环控制器的输出为：

(38)

为了分析设计的母线电压外环闭环控制系统的稳定性，本文构造Lyapunov函数为：

(39)

求导可得：

(40)

其次，可得：

(41)

(42)

将式子带入可得：

(43)

4 仿真结果与分析

本节为了验证所提出的基于新型趋近律的直流微电网母线电压滑模控制器的合理性和工作性能，采用图4所示的直流微电网母线电压控制结构，在Simulink上搭建系统模型。

将控制器的参数设置为：滑模控制器增益k=1 200；ε=6 000；β=3。PI控制器增益Kp=0.75；KI=45。

仿真结果的具体说明为：图6为系统在常用的PI控制和文中所提的直流微电网母线电压的ESO-NRSMC控制方法下的直流微电网母线电压的阶跃响应对比图；图7为在直流侧电阻性负载突变的情况下，母线电压的波形对比图；图8为在恒功率型负载突变的情况下，母线电压的波形对比图；图9为在参数C失配情况下，母线电压的波形对比图。

具体的结果分析如下所示。

1)阶跃性能比较。

从图6可以看出，直流微电网母线电压在PI控制的作用下起动迅速，但是会有较大的超调，并且到达稳态的速度较慢；而在所提的ESO-NRSMC控制策略下可以几乎实现无超调，且仅需约0.015 6 s便能快速地达到稳定状态。所提的ESO-NRSMC器相比于PI控制器在启动特性和鲁棒性方面更具有优势。

图6 直流微电网的母线电压阶跃响应图

2)负载波动性能比较。

由图7和图8可以看出，在直流微电网直流侧电阻性负载和直流侧功率性负载突然减半时，直流微电网母线电压在PI控制的作用下较为敏感，母线电压波动的幅度较大，并且波动后需要较长的调节时间才能够恢复到稳定状态；而在本文所提的ESO-NRSMC控制策略的作用下，当直流侧电阻性负载和直流侧恒功率性负载突然减半时，仍然能够维持较好的动态性能，可以快速地恢复到稳定状态，并且该控制方法采用了一种新型趋近律方法，使得控制器对抖振的抑制能力也得以提高。

图7 直流侧电阻性负载突变时的电压波形图

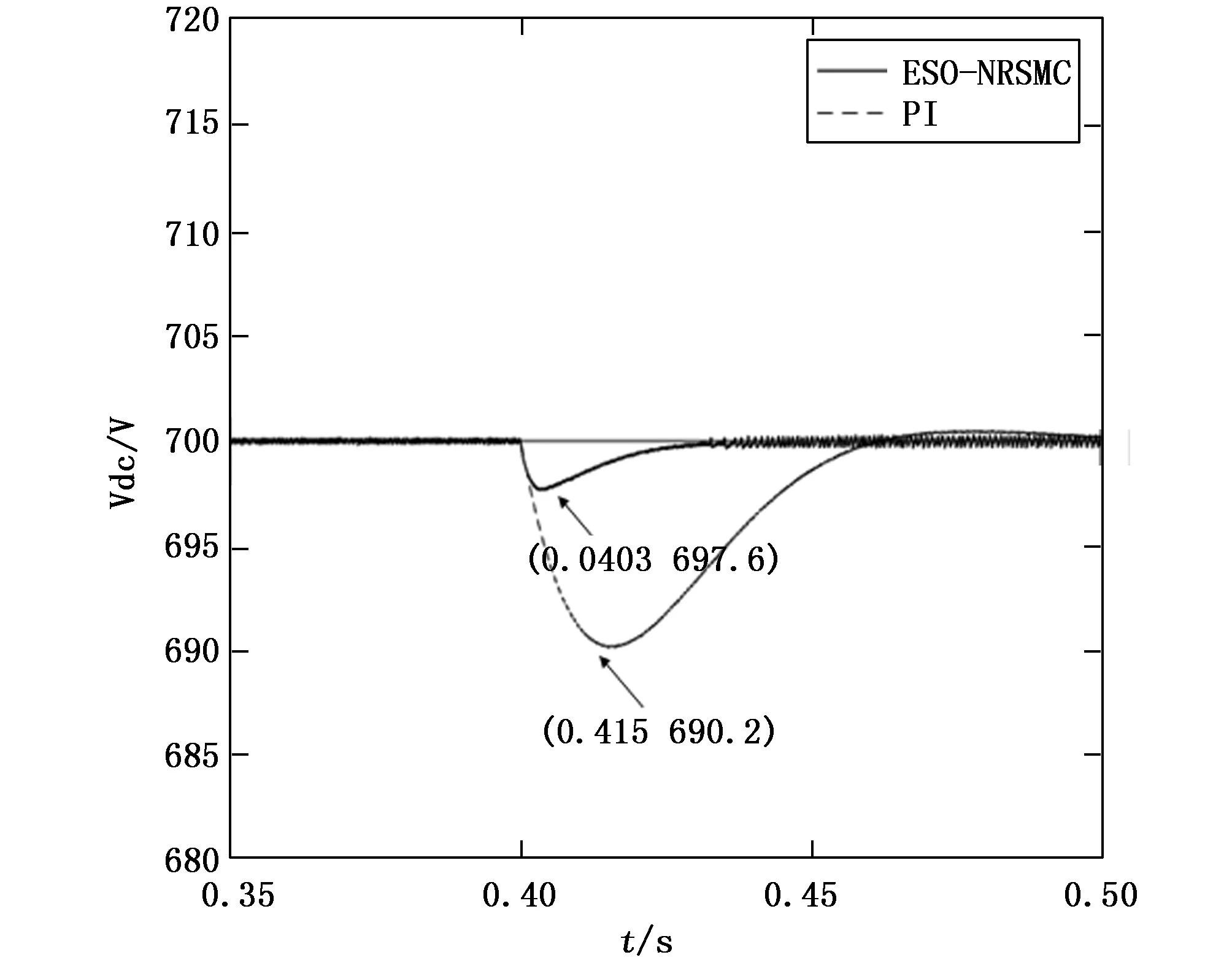
图8 直流侧恒功率性负载突变时的电压波形

3)参数敏感性比较。

在微电网运行过程中，可能会出现系统的模型参数与控制器的参数不匹配的情况，此处将直流母线电容设置为。由图9可以看出，在控制系统的参数C失配情况下，PI控制器对参数C失配的情况较为敏感，会恶化瞬态响应，超调量也较大。而所提ESO-NRSMC控制器对参数C变化的情况不敏感，瞬态响应较为良好，超调不明显，仅需要0.022 s就能在较快的时间内到达稳定状态。

图9 参数C发生变化时直流微电网的母线电压波形图

5 结束语

本文针对于直流微电网母线电压控制系统中存在的母线电压稳定性的问题，提出了一种ESO-NRSMC控制方法。该方法应用扩张状态观测器，观测到直流母线控制系统中的非线性部分与外部扰动的部分，并且对其进行前馈补偿，将所观测到的状态扰动值反馈到该控制器之中，有效地提高了直流微网母线电压的稳定性能。同时，还通过采用一种新型趋近律的方法来设计该滑模控制器，使得该控制器在拥有较快的收敛速度的同时，又可以有效地抑制系统出现的高频抖振。之后，还通过引入lyapunov函数，证明该控制器的稳定性。最后，将本文所设计的直流微电网母线电压控制方法与目前常用的PI控制方法作对比实验，验证了本文所设计的控制器ESO-NRSMC的可行性和优越性，证明本文所设计的控制器ESO-NRSMC可以有效地解决直流微电网在参数摄动和负荷波动情况下，母线电压难以维持其平稳运行的难题。