一种针对动目标的声呐波形设计算法∗

王鹤霖

（昆明船舶设备研究试验中心 昆明 650000）

1 引言

声呐波形设计技术一直是声呐研究中的焦点［1～4］。与传统调频信号相比，相位编码信号具有平均发射功率大、灵活多变等优点，这使得相位编码信号尤其受到重视［5～6］。由于水下航行器在工作时的运动速度较快，声呐系统接收到的目标回波的多普勒较高［7］，为了提高声呐系统在高多普勒时对弱目标的时延分辨力就需要设计一种在高多普勒条件下具有较高时延分辨力的发射波形。

提升发射波形时延分辨力的波形设计方法可分为零多普勒条件下提升发射波形时延分辨力的波形设计算法和高多普勒条件下提升发射波形时延分辨力的波形设计算法两类。第一类算法中比较经典的有CAN算法［8］、MISL算法［9］和MWISL算法［10］，这三种算法主要考虑的是通过最小化加权累积旁瓣水平WISL（Weighted Integrated Sidelobe Level）来压制自相关旁瓣水平，从而达到提高对弱目标的时延分辨力的目的。CAN算法主要是基于循环最优化方法CA（Cyclic Approach）推导的，而MISL算法和MWISL算法则是基于优化最小化方法 MM（Majorization Minimization）［11］推导的。目前对第二类算法的研究较少，比较经典的有AFSIM算法［12］，但该算法的实时性较差。本文主要研究的是第二类波形设计算法，通过将CA方法与MM方法结合提出了一种新的波形设计算法。经仿真验证，本文提出算法与AFSIM算法相比效果更好、实时性更强。

2 问题建模

将长度为N的相位编码发射序列表示为s=[s1,…,sN]T，则将发射序列与多普勒频移为 f的回波做互相关的输出为

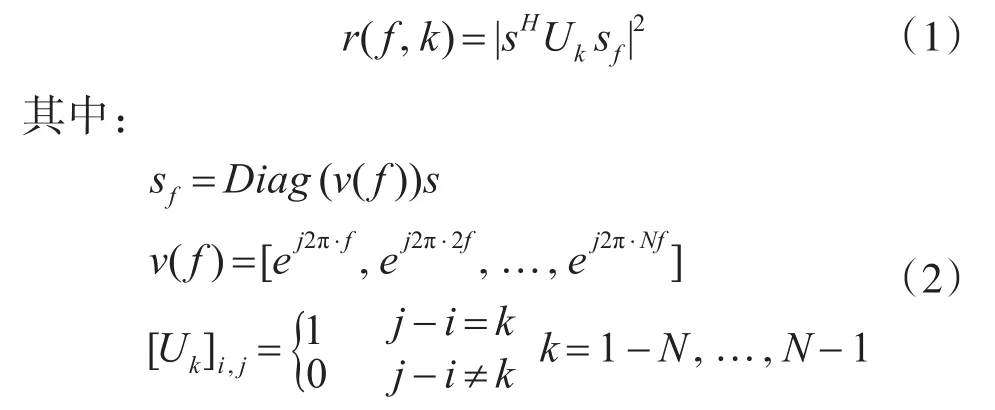
为了使生成序列与产生多普勒频移后的接收信号的互相关更接近期望互相关，就提出了如式（3）所示最小二乘代价函数：

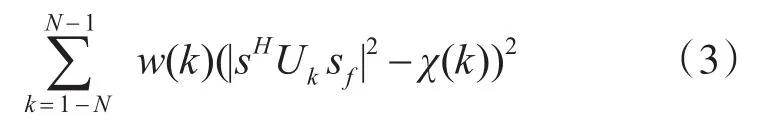
其中 χ(k)为期望互相关，w(k)为权重。对于需要提升弱目标分辨能力的时延区间，可将其对应的χ(k)和w(k)分别设为0和1。由于该目标函数为变量s的八次函数，难以解决，所以就利用下面的与该目标函数“近似相等”的四次函数来作为目标函数。

由于式（4）中的取模运算难以处理，就引入了一组辅助变量 θ=[θ1-N,θ2-N,…,θN-1]来将原问题中的取模运算简化。简化后的问题为

接下来就是解决式（5）所示的优化问题的具体推导过程。

3 循环最优化算法

依据CA方法的基本原理，在优化过程中要交替对两个优化变量θ和s进行优化。

3.1 变量θ的优化

由式的形式可得，当s为定值时，使其目标函数取得最小值的θ为

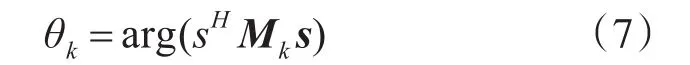
3.2 变量s的优化

当θ为定值时，将ϒ(s)完全展开并忽略常数项后可得如下的优化问题：

由于式（9）所示的ϒ1(s)是一个四次函数，难以通过直接优化来寻找其最小值，所以在优化过程中就需要先利用MM方法降低其幂次，再解决其优化问题。

其中 S(t)=s(t)(s(t))H，D的最大特征值 λmax=maxk为 N×N 维的单位矩阵。

由于发射序列s具有恒模的特点，则可得λmaxvec(S)Hvec(S)的值为 λmaxN2。除此之外，u1(S,S(t))的第三项中不包含变量S，是一个与变量S无关的量。忽略式中的与S无关的量后，其可转化为下面的二次问题。

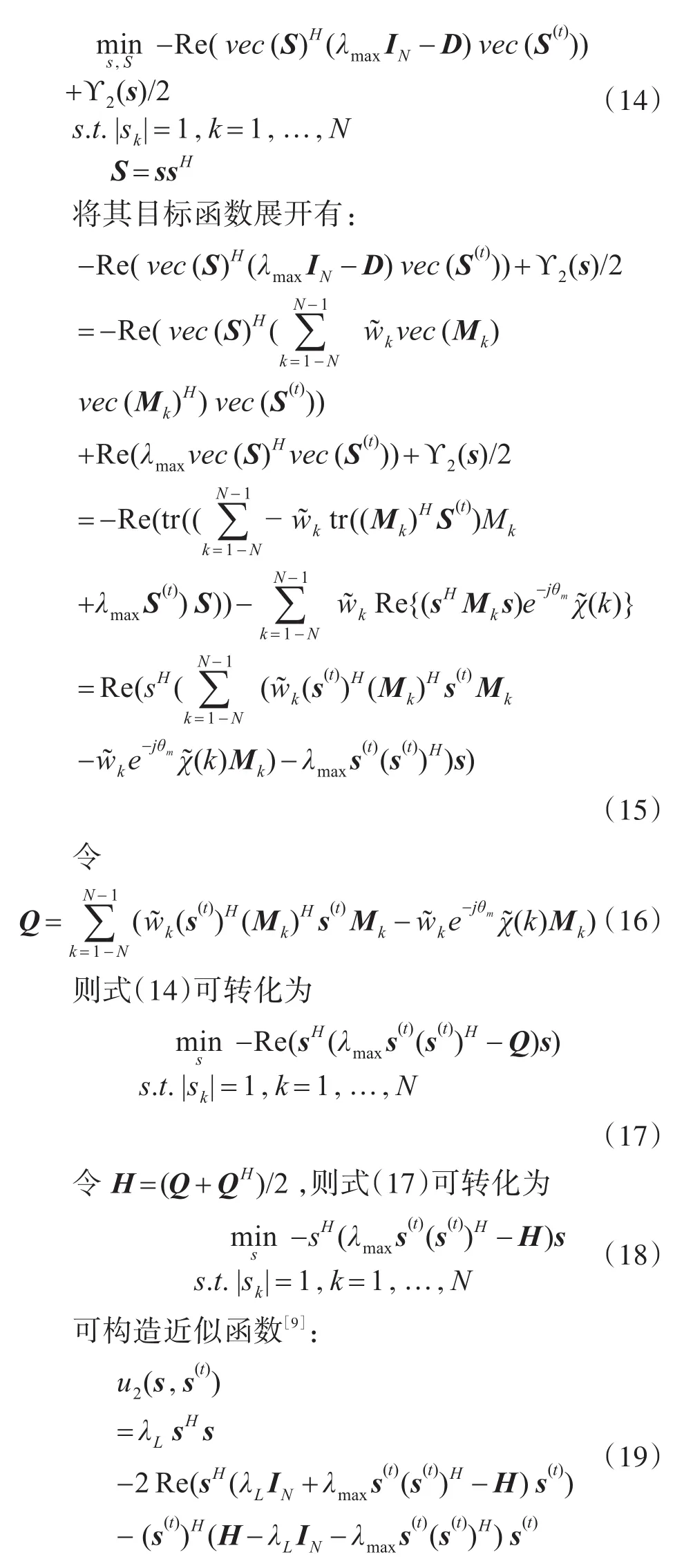
其中λL为H-λmaxs(t)(s(t))H的最大特征值的上界。

由于发射序列s具有恒模的特点，则可得λLsHs的值为λLN。除此之外，u2(s,s(t))的第三项不包含变量s，是一个与变量s无关的量。忽略式中的与s无关的量后，其可转化为下面的一次问题

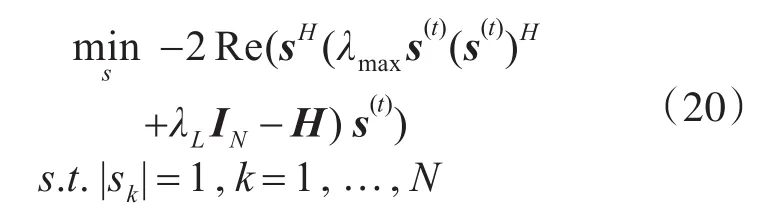
下面的工作就是估计矩阵H-λmaxs(t)(s(t))H的最大特征值的上界λL。

3.3 算法流程总结

将本文提出的算法命名为AC算法，则AC算法的步骤可以总结为

1）给定初始化序列、需要提高时延分辨力的多普勒频率和时延区间；

2）用式（7）计算θ；

3）用式（26）计算 y；

4）用式（28）计算 s；

5）重复步骤2）、3）、4），直到算法收敛。算法收敛的条件一般设置为两次迭代中序列变化量的二范数小于设定的门限。

4 仿真实验

为了验证本文推导的针对动目标的波形设计算法的效果，下面进行了计算机仿真，主要对比了AC算法与AFSIM算法的时延分辨力与运行速度。

仿真条件为：编码序列长度为N=50，需要提高时延分辨力的多普勒频率和时延区间分别为和[15,20]∪[25,27]，收敛条件为两次迭代中序列变化量的二范数小于10-3。图1为两种算法生成序列的考虑多普勒的自相关的对比。从图1中可以看出，AC算法生成序列在多普勒频率为、时延为[15,20]∪[25,27]的区间内的相关明显低于AFSIM算法，这证明AC算法生成的序列具有更高的时延分辨力。除此之外，AC算法仅用2.16s就达到了收敛条件，而AFSIM算法达到收敛条件则用了242.30s，这也展现出了AC算法的实时性强的特点。图2为AC算法的目标函数随迭代时间的变化。从图2中可以看出，AC算法具有单调特性，且在收敛时的目标函数值可以达到-37dB以下。

图1 AC算法与AFSIM算法效果对比

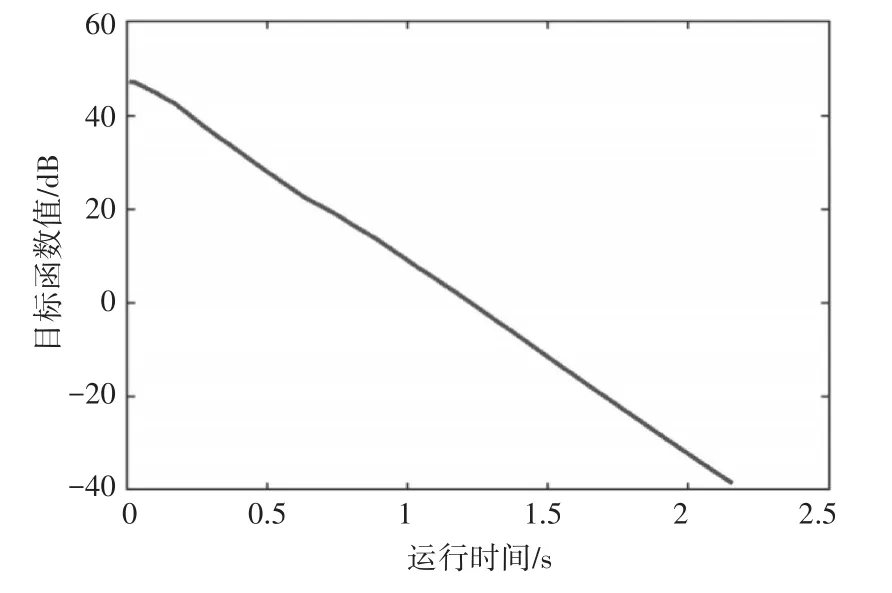
图2 AC算法的目标函数随迭代时间的变化

5 结语

本文提出了一种可在高多普勒条件下提升发射波形时延分辨力的AC算法。首先以最小化考虑多普勒的自相关函数与期望自相关函数的误差为目标提出了优化问题。然后基于CA方法和MM方法推导出了AC算法。最后证明了与AFSIM算法相比，本文提出的AC算法具有更好的时延分辨力和更强的实时性。