联合对海打击兵力配备方案优选方法研究∗

刘 蜀

（91336部队 秦皇岛 066326）

1 引言

现代海战中，对水面舰艇的打击主要由反舰导弹实施。由于水面舰艇对空探测、指挥控制、防空反导能力的迅速提升，达成预期攻击效果的难度也急剧提升。因此，在预定打击区域，组织各军兵种，联合实施岸海空协同同对海打击，是能够充分调动一切可用资源，完成预定打击任务的有效手段［1～3］。研究兵力配备方案优选方法，首先要提出兵力配备方案集，继而研究确定优选指标、指标值规范化处理方法、优选算法，通过定量计算确定打击兵力配备方案。

2 打击兵力配备方案列举

联合对海打击兵力配备方案优选的前提是列举出合理的配备方案，形成配备方案集。其实施方法如下：

首先，梳理出在预定打击区域我方可运用的岸海空兵力及其带弹数量，为配备方案列举提供依据。一般来说，可执行对海打击的兵力包括战斗机/战斗轰炸机、轰炸机、驱护舰、导弹艇、岸舰导弹、潜艇，其带弹数量分别为2枚～4枚、6枚、4枚～8枚、4枚～8枚、8枚、6枚。

其次，分析预定打击的水面舰艇的型号、数量、防空能力，对打击理论用弹量进行定量计算［4～7］。

最后，按照排列组合列举大于等于理论用弹量（大于量不超过10%）的打击兵力配备方案，形成打击兵力配备方案集，设配备方案个数为n，则配备方案集用X={x1…xn}表示。

3 优选指标确定

得到打击兵力配备方案集后，进行最优方案优选。优选过程如下：首先确定优选指标及各指标取值情况，继而对指标值进行规范化处理，最后应用优选算法对各方案进行优劣评分，得到最优方案。

开展打击兵力配备方案优选，需从组织协同、自身安全、攻击效果等方面综合衡量，具体考虑以下因素：兵力出动种类、兵力出动数量、兵力被攻击风险、行动隐蔽程度、目指需求、用弹量、地利因素。将上述因素定为优选指标，分别用 f1…f7表示，如图1所示。

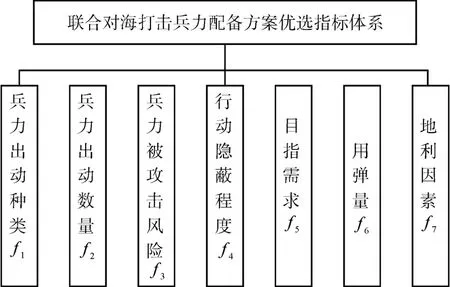
图1 联合对海打击兵力配备方案优选指标体系

上述指标的取值及取值的优劣规定如下：

兵力出动种类：分为单一型号、单一兵种、2个兵种、3个兵种四种情况，兵力出动种类越少，越好组织协同。

兵力出动数量：兵力出动数量越少，越好组织指挥。

兵力被攻击风险：通过分析研究上述兵力活动空间、机动性、攻防能力，结论如下，战斗机/战斗轰炸机、潜艇低，导弹艇中，轰炸机、驱护舰、岸舰导弹高，综合分析结论为低、较低、中、较高、高五个等级的定性描述。

行动隐蔽程度：通过分析上述兵力目标特性，结论如下，潜艇、导弹艇高，战斗机/战斗轰炸机中，轰炸机、驱护舰、岸舰导弹低，综合分析结论为低、较低、中、较高、高五个等级的定性描述。

目指需求：上述兵力对目标指示的需求程度，按照战斗机/战斗轰炸机、轰炸机、驱护舰、导弹艇、潜艇、岸舰导弹的顺序依次升高，需求程度越低，行动组织、通信保障越简单，综合分析结论为低、较低、中、较高、高五个等级的定性描述。

用弹量：用弹量为各兵力配备方案的导弹发射数量，考虑到冗余量，该指标在一定范围内越大越好，超过最佳值，则越大越差，最佳值选取根据目标情况临机确定。

地利因素：若兵力配备方案有导弹艇，且作战区域附近有可隐蔽待机的岛礁区、民船，则地利因素好；若兵力配备方案有岸舰导弹，但岸舰导弹射击扇面不能完全覆盖预定打击海区，则地利因素差。

4 指标值规范化处理方法

上述优选指标中，兵力出动种类、兵力出动数量、兵力被攻击风险、目指需求为成本型指标，即指标值越低越好；行动隐蔽程度为效益型指标，即指标值越高越好；用弹量为固定型指标，即越接近某个固定值越好。此外，上述指标中既有定性评价的指标，又有可定量计算的指标，定量的指标取值范围也不尽相同。因此，在方案优选之前，需首先将指标值进行规范化处理，统一规范化为［0，1］区间内的实数。方法如下：

兵力出动种类：令单一型号、单一兵种、2个兵种、3个兵种取值分别为1、2、3、4。该指标为成本型指标，通用规范化方法如下：

其中 rij为第i(1≤i≤7)个指标下第 j(1≤j≤n)个备选方案的取值，rimin、rimax分别为该指标的最小值、最大值，μij为规范化值，下同。

兵力出动数量：同为成本型指标，采用成本型指标通用规范化方法计算。

兵力被攻击风险：该指标为定性指标，可将风险等级从低到高分别取值为1、2、3、4、5。该指标为成本型指标，采用成本型指标通用规范化方法计算。

行动隐蔽程度：该指标为定性指标，可将隐蔽程度从低到高分别取值为1、2、3、4、5。该指标为效益型指标，通用规范化方法如下：

目指需求：该指标为定性指标，可将需求程度从低到高分别取值为1、2、3、4、5。该指标为成本型指标，采用成本型指标通用规范化方法计算。

用弹量：该指标为固定型指标，通用规范化方法如下：

地利因素：若为好，则取值为1；若为差，取值为0；不涉及地利因素，取值为0.5。

通过规范化处理，得到各方案指标值的相对优属度矩阵 μ=(μij)7×n。

5 优选算法

优选算法需体现如下两个因素：综合各个指标，从当前备选方案中进行优选，由于指标值已规范化，因此可规定优选出的方案需接近理想方案（各指标值均为1）同时远离负理想方案（各指标值均为0），与TOPSIS算法的思路基本一致；地利因素很多方案不涉及，因此确定各指标的权重值时，需针对是否涉及地利因素对初始权重进行调整。

综上所述，本文采用权重可调整的TOPSIS改进算法进行方案优选。

5.1 变权加权算法

变权是相对于常权而言的。在多属性决策中，决策对象xj的常权综合函数Mxj常用如下公式表示：

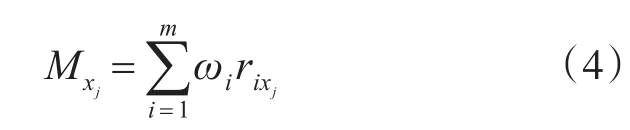
常权综合考虑了各个指标的相对重要性，使综合值在一定程度上体现了各个指标的重要程度，由于其简单和具有一定的合理性而被广泛应用。但是，在多属性决策中，有时不仅需要考虑各评估指标的相对重要性，还应该考虑指标值的变化对评估指标相对重要性的影响。实现方法为通过指标值的大小对指标的权重进行适当的重新分配。

变权加权的思想、算法由汪培庄等教授提出并论证，其主要性质如下［9～11］：

3）惩罚型：ω(rj)是关于 rj中每个分量 rij（i=1,2,…,m）的单调不增向量函数；或激励型：ω(rj)是关于rj中每个分量rij（i=1,2,…,m）的单调不减向量函数；或混合型：ω(rj)是关于rj中 p个分量rij的单调不增（或减）向量函数，而关于其余m-p个分量的单调不减（或增）向量函数，其中0≤p≤m。

则称ω(rj)为1个变权向量。

5.2 TOPSIS投影算法

逼近于理想解的排序方法（Technique for Or⁃der Preference by Similarity to Ideal Solution，TOP⁃SIS）是为解决多目标决策问题而提出的一种接近于线性加权法的排序方法。这种方法的基本思想是：所选择的满意方案应尽可能地接近相对理想方案同时又尽可能地远离相对负理想方案。

定义理想方案为x+，其目标相对优属度为g=(g1,g2,…,gm)T=(1,1,…,1)T；负理想方案为x-，其目标相对优属度为b=(b1,b2,…,bm)T=(0,0,…,0)T。 备 选 方 案 xj(j=1,2,…,n)与理想方案x+的接近程度用加权欧氏距离度量：

与负理想方案的远离程度也用加权欧氏距离度量：

理想方案与负理想方案之间的加权距离表示为

其中ωi为目标 fi(i=1,2,…,m)的权重。

在TOPSIS中，备选方案xj(j=1,2,…,n)与理想方案x+的相对接近度为

显然，cj=0时xj为负理想方案，cj=1时xj为理想方案，cj越大表示xj越接近于x+，于是可由cj(j=1,2,…,n)从大到小的顺序确定出备选方案集X的优劣排序。但是TOPSIS在有些情况下并不能有效地兼顾备选方案接近理想方案与远离负理想方案这两方面因素。例如：假设备选方案A与理想方案的距离为0.3，与负理想方案的距离为0.4；备选方案B与理想方案的距离为0.376，与负理想方案的距离为0.5。以备选方案A为参照进行比较，备选方案B同时远离正负理想方案，但与负理想方案的距离增幅大于与理想方案的距离增幅，因此综合考虑的结果应为备选方案B优于备选方案A，但是用TOPSIS却得出了相反的结论。为此，对TOPSIS进行改进，其基本思想是：将n个备选方案与理想方案、负理想方案都抽象为m维方案空间中的点，每个方案的相对优属度即该方案在空间中的坐标值。将代表各个备选方案的点垂直投影在理想方案点与负理想方案点的连线上。投影点距离理想方案点越近的同时距离负理想方案点也就越远，意味着该点代表的备选方案越优，反之则越劣。如图2所示。

图2 方案点垂直投影示意图

具体计算可按如下方法进行。记dq(xj,x+)=a，dq(xj,x-)=b，dq(x+,x-)=c，∠xjx-x+=θ，并令 pj长度为方案xj的投影值 pxj。

显然，0≤pxj≤1，且 pxj值越大表示方案越优，于是可由pxj值按降序排列确定出方案集X的优劣排序。当两个备选方案具有相同的 p值时，此时采用TOPSIS即可辨别优劣［12］。

5.3 变权加权TOPSIS投影算法

将上述两个算法进行结合，得到本文采用的变权加权TOPSIS投影算法，计算流程如下：

Step1：计算每个方案在各个指标下的指标值，采用规范化方法对指标值进行规范化，得到指标值的相对优属度矩阵μ。

Step2：确定各指标的初始权重：构造层次分析法中的重要性对比矩阵，邀请专家进行打分，得到各指标的初始权重向量（即常权向量）ω=(ω1,ω2,…,ω7)T=（0.22，0.18，0.15，0.19，0.16，0.1，0）T。由于大多数方案不涉及地利因素 f7，因此初始权重向量中ω7=0。

Step3：针对方案xj（j=1,2,…,n）确定状态变权函数。综上分析，前6项指标权重不需要随其指标值改变，因此对于(i=1,2,…,6)。对于 f7，当r7j=0.5时，表示 xj不受地利因素影响，则不变，其值为 0；当r7j=1或r7j=0时，表示xj受地利因素影响，则令，即地利因素有一定权重值。

Step4：对xj重新分配后的权重进行归一化处理，得到 xj的变权权重向量 ω(rj)=(ω1(r1j),ω2(r2j),，计算公式如下：

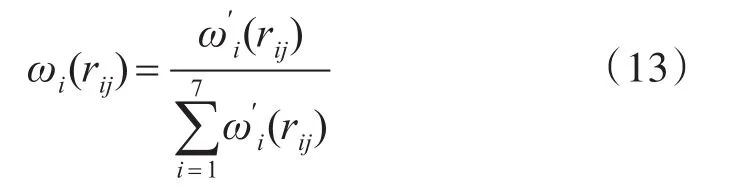
Step5：采用TOPSIS投影算法，首先计算各方案的与理想方案、负理想方案的加权欧氏距离，继而计算投影值，最后对投影值进行排序，投影值最大的即为最优方案。

6 案例分析应用

设计一个作战想定，运用本文提出的优选方法进行案例分析，以检验方法的可行性及有效性。

6.1 作战想定

假设当前态势如下：

敌方组织1艘驱逐舰、3艘护卫舰，为3艘登陆舰护航，意图夺占我方关键岛屿。

我方决心在预定打击海区消灭敌登陆编队，可动用的兵力有：驱护舰8艘、战斗机12架、战斗轰炸机10架、岸舰导弹中队1个。其中岸舰导弹射击扇面不能完全覆盖预定打击海区。

6.2 打击兵力配备方案集生成

采用参考文献［5］提出的计算方法，分析敌方登陆编队的舰型、排水量及武器装备，计算对海打击的理论用弹量。计算结果如下所示：驱逐舰22枚、护卫舰13枚、登陆舰10枚，合计91枚。按照用弹量不超过理论用弹量10%的要求，即用弹量不大于100枚。

按照战斗机2机1编队，每机挂反舰导弹2枚，战斗轰炸机2机1编队，每机挂反舰导弹4枚，驱护舰每舰配反舰导弹4枚，岸舰导弹每中队配反舰导弹8枚，结合可动用兵力规模对打击兵力配备方案进行列举，结果如下：

方案1：战斗机12架、战斗轰炸机10架、驱护舰8艘，用弹量96枚；

方案2：战斗机12架、战斗轰炸机10架、驱护舰7艘，用弹量92枚；

方案3：战斗机12架、战斗轰炸机10架、驱护舰7艘、岸导中队1个，用弹量100枚；

方案4：战斗机12架、战斗轰炸机10架、驱护舰6艘、岸导中队1个，用弹量96枚；

方案5：战斗机12架、战斗轰炸机10架、驱护舰5艘、岸导中队1个，用弹量92枚；

方案6：战斗机12架、战斗轰炸机8架、驱护舰8艘、岸导中队1个，用弹量96枚；

方案7：战斗机12架、战斗轰炸机8架、驱护舰7艘、岸导中队1个，用弹量92枚；

方案8：战斗机10架、战斗轰炸机10架、驱护舰8艘、岸导中队1个，用弹量100枚；

方案9：战斗机10架、战斗轰炸机10架、驱护舰7艘、岸导中队1个，用弹量96枚；

方案10：战斗机10架、战斗轰炸机10架、驱护舰6艘、岸导中队1个，用弹量92枚；

方案11：战斗机10架、战斗轰炸机10架、驱护舰8艘，用弹量92枚；

方案12：战斗机10架、战斗轰炸机8架、驱护舰8艘、岸导中队1个，用弹量92枚；

方案13：战斗机8架、战斗轰炸机10架、驱护舰8艘、岸导中队1个，用弹量96枚；

方案14：战斗机8架、战斗轰炸机10架、驱护舰7艘、岸导中队1个，用弹量92枚；

方案15：战斗机6架、战斗轰炸机10架、驱护舰8艘、岸导中队1个，用弹量92枚。

上述方案用x1…x15分别表示。

6.3 打击兵力配备方案优选

采用变权加权TOPSIS投影算法进行计算。

经专家分析确定，用弹量最佳值为95枚。首先按照上述7个优选指标及其规范化处理方法分析上述15个备选方案，得到各备选方案的决策矩阵r7×15以及相对优属度矩阵 μ7×15结果如下：

继而计算指标权重。初始权重ω已确定。根据状态变权函数计算方法，前6项指标的ω′i(rij)=ωi(i=1,2,…,6)，因部分备选方案运用了岸舰导弹，但是其射击扇面不能完全覆盖预定打击海区，所以

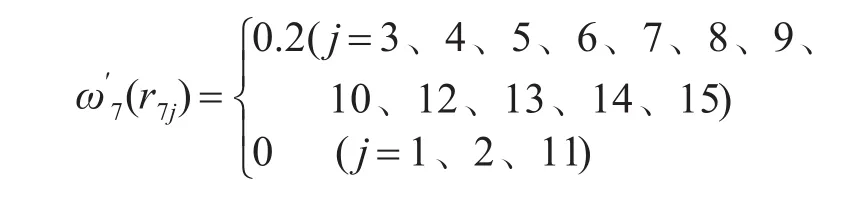
采用式（13），计算各个备选方案的变权权重。得到

采用式（6）、（7）、（8），计算正负理想方案间的距离以及各备选方案与正、负理想方案间的距离。结果如下：

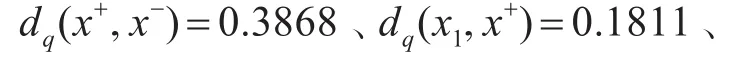
采用式（12），计算各备选方案的投影值pxi。结果如下：

7 结语

本文基于变权加权算法和TOPSIS算法，进行适当改进、集成，提出了一种联合对海打击兵力配备方案生成与优选的方法。通过通过案例分析应用，检验了该优选方法的合理性、有效性，表明该方法能够快速准确地开展联合对海打击兵力配备方案优选。下一步需要充分运用机器学习、人工智能等算法，针对备选方案生成与初步筛选环节，开展深入研究，以便更加迅速地开展方案优选。