六维力传感器的优化设计

甘俊，付荣豆

（北方工业大学 机械与材料工程学院，北京，100144）

0 引言

六维力传感器是自动化[1,2]，机器人[3,4]和航空航天领域最重要的传感器之一。它可以同时测量三维力和三维扭矩信息，根据六组分离信息识别其环境，主要用于力和力位置控制，如焊接、研磨、装配、轨迹跟踪等。目前，六维力传感器主要应用在机器人的末端，用于感知外界环境，是机器人高质量控制的重要传感元件[4,5]。

针对多维力传感器之间存在的维间耦合问题[6,7]，本文在传统的十字梁弹性体结构的基础上进行弹性体结构优化和对电路的解耦设计，提出了一种解耦能力更强、精度更高的新型六维力传感器弹性体结构和电路解耦方式，且该传感器具有结构简单、易于加工，测量精度高，维间耦合误差小等优点。

1 六维传感器的结构

六维力传感器弹性体的结构设计直接决定了传感器的性能。本文在如图1所示的六维力传感器弹性体结构的基础上对其进行了优化设计，优化后的弹性体结构如图2所示。四根弹性梁组成十字交叉形，弹性梁为十字变截面的弹性结构，四个角为固定端，中间的中心凸台为测量平台，与被测量物体连接，弹性梁和轮缘连接处为浮动梁连接，中心凸台与浮动梁之间为弹性体连接，有四个沿圆周均匀分布的弹性体主梁，传统的传感器十字型截面面积保持不变，在主要尺寸不变的情况下，优化后的十字型截面面积沿着测量平台到浮动梁方向逐渐减少，用于测量空间中的六个分力。

2 有限元仿真

确定了弹性体的结构形式后，利用有限元软件Ansys对优化前后两种结构的弹性体进行静力学分析，确定在单维力作用下结构变形最大的区域。本文只给出优化后的十字型变截面弹性体有限元变形图。

2.1 弹性体有限元模型

利用Ansys对十字变截面弹性梁进行静力学仿真分析，确定弹性梁在单维力作用下结构的最大变形区域。

弹性体结构的主要尺寸如表1所示。

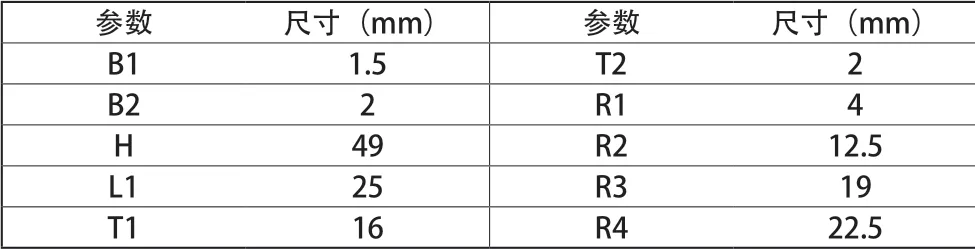
表1 主要结构尺寸

弹性体材料为7075高强度铝合金，其杨氏模量为10＾5MPa，材料密度为7850kg/m3，泊松比为0.25。利用ANSYS有限元软件对六维力/力矩传感器进行三维实体建模，并用高精度实体单元SOLID186对模型进行网格划分。

2.2 结构应变分析

将四个螺钉孔内表面设置成固定约束，将中心平台的中心孔设置成载荷约束，当扭矩分析时就添加扭矩载荷属性，当受力时就设置力载荷属性。弹性体变形图如图3所示。

由于结构对称，Fy与Fy的受力情况等效，Mx与My的受力情况等效，故不在此列出。x轴、z轴方向的受力和力矩分别为150N、10N.m。

如图3所示，在Fx=150N单独作用下，y向浮动梁和弹性梁的应变相较于与x轴方向的弹性梁应变较小，可忽略不计，因此，力Fx可以通过测量y向弹性梁的应变得到，Fy与此类似；弹性体在受到Fz=150N单独作用时，x向主梁和y向主梁均发生了弯曲变形，因此Fz可以通过检测弹性梁上下表面节点的应变获得；弹性体受到力矩Mx=10N.m时，y向主梁分别向相反的方向发生弯曲变形，因此，力矩Mz可以通过检测y向弹性梁上下表面节点的应变获得；弹性体受到力矩Mx=10N.m时，x向主梁和y向主梁均发生了弯曲变形，因此，力矩Mz可以通过检测主梁侧面节点应变获得。因此，可将弹性梁最大应变位置作为传感器测量桥路的贴片位置。

3 桥路的解耦设计

弹性体的每一维受力可使用4只应变片构成全桥电路来检测，6组桥路共计24只应变片，组桥示意图如图4所示。

各桥路的输出电压为：

其中，ε为弹性体上第i个传感器的应变值，U为激励电压，K为应变片的灵敏系数。

桥路解耦的电路原理分析：影响六维力传感器精度的因素有很多，其中最主要的因素是维间耦合。解决维间耦合问题一方面是从传感器弹性体自身结构上采取措施，另一方面是采取电路或信号处理方法。因此，在确定弹性体结构及贴片位置后，需要对解耦电路进行合理的设计。

此结构采用全桥电路连接，左右两个梁上贴上12只应变片、上下两根梁贴上12只应变片，对称分布，共24只应变片，形成6路输出电信号，具体贴片位置见图5，图中的R9/R10为梁的上下两面，同理有R11/R12，R15/R16，R17/R18，R19/R20。全桥电路的相对应变片贴在弹性体梁的变形相同的地方，电路上相邻应变片贴在梁上变形相反的地方，组合成全桥后应变放大四倍输出，同时对噪声温度等有一定差分消除的作用，从而实现了电路解耦的设计。

4 实验结果

4.1 各桥路输出

为了确定弹性梁上的贴片位置，需要找到在单位力作用线的梁上最大应变的位置。为了确定电阻应变片的精确位置，需要分析十字梁上节点距中心凸台的距离与应变大小的对应关系。为此，利用了Ansys的路径映射技术，设置一条直线路径，该路径位于弹性体十字变截面弹性梁表面的中线上，中心凸台与弹性体相交处为顶端，到浮动梁处为末端，将受力/力矩的应变结果映射到该路径上，结果如图6所示。

由图可知：在单维力Fx=150N作用下，贴片位置位于路径的起点1.1669mm处，桥路的测量值最大；在单维力Fz=150N作用下，贴片位置位于路径的起点2.0963mm，桥路的测量值最大；在单维力Mx=10N.m作用下，贴片位置位于路径的起点2.5622mm处，桥路的测量值最大；在单维力Mz=10N.m作用下，贴片位置位于路径的起点1.8892mm处，桥路的测量值最大。根据上述分析结果，选取应变最大的节点作为贴片点。

4.2 维间耦合分析

理想的六维力传感器，每一个方向输出的电压值与该维度的作用力/力矩的大小成正比，与其余五个方向的作用力/力矩大小无关。下面通过表2和表3对比分析了对十字梁优化前后两种结构的六维力/力矩传感器的维间耦合效应。

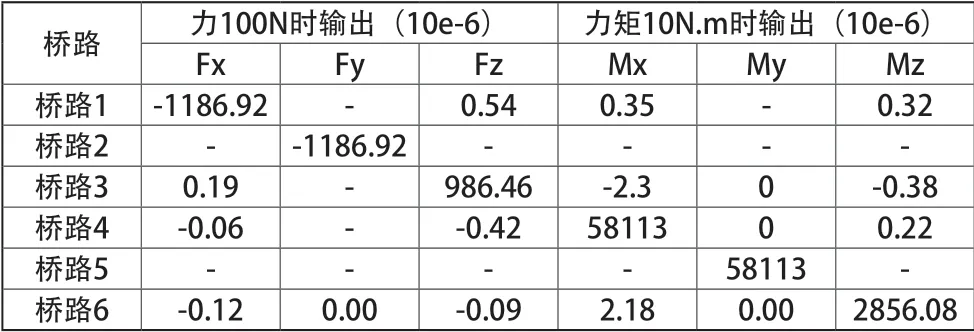
表2 优化后的十字型截面各维力/力矩在不同桥路的输出

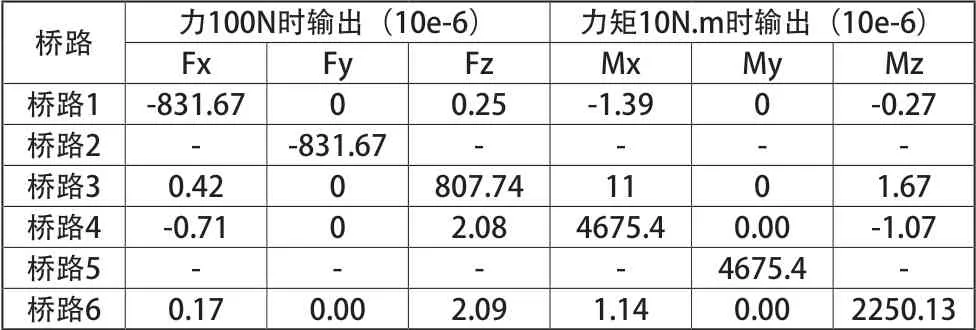
表3 传统十字型截面各维力/力矩在不同桥路的输出

由表可知，Fx主要影响桥路1的输出，Fy主要影响桥路2的输出，Fz主要影响桥路3的输出，Mx主要影响桥路4的输出，My主要影响桥路5的输出，Mz主要影响桥路6的输出，各维力之间耦合误差小。

通过十字截面梁弹性体和十字变截面梁弹性体的耦合度对比发现，在相同的尺寸和载荷条件下，经计算十字型截面的弹性体结构的耦合度为1.36%，优化后的十字型变截面的弹性结构的耦合度为0.23%。优化后的十字型截面的弹性体结构的微应变均有一定程度提升，尤其是对本身应变就偏弱的Fx的提升到300个微应变，增幅46%，其他方向均有部分提升。

5 结论

本文通过对十字型截面的弹性体结构和优化后的变截面十字型截面的弹性体结构的对比分析发现，优化后的变截面的弹性体自解耦效果更好、精度更高。本文通过对传感器的静力学仿真，分析了贴片点的位置变化对桥路输出的影响，并确定了各测量桥路的最佳贴片位置和组桥解耦电路的设计方式。最后对传感器耦合度进行了分析，验证了优化后的传感器解耦能力更强、灵敏度高、维间耦合小等优点，具有较强的实用性。