贝叶斯网络方法能为教育研究带来什么? *
顾 昕 毛梦琪 马淑风 陈森宇
(1. 华东师范大学教育学部教育心理学系,上海 200062;2. 曼彻斯特大学健康科学学院,曼彻斯特 M13 9PL )
一、引言
教育实证研究强调数据证据,研究者根据理论提出假设、设计实验、收集数据、分析数据,得到支持或反对研究假设的结论。但是传统数据分析方法在处理复杂、多元、动态的教育实证研究数据时面临诸多挑战。首先,随着教育研究问题的复杂化,研究对象通常是包含多个维度、多个层次的复杂建构,传统方法如方差分析、回归分析等已无法满足教育数据分析的实际需求。其次,统计分析是基于概率的推断,具有不确定性。传统方法得到的研究结论通常表述的是差异的显著性或影响的大小、方向等,例如“不同家庭教养方式下的子女学业成绩有显著差异”“父母受教育程度越高,其子女学业成绩越高”,这些研究结论并未体现数据证据的不确定性。再次,传统分析流程要求预先设置被试抽样、观测变量、样本容量等,得到的数据证据不可累积和更新。然而,教育是通过教师和学生的互动来实现的,学生的发展是动态的,教育数据是过程性的,模型建构是不断变化的。动态的教育数据分析需要证据的积累与更新,需要研究结果的实时反馈。那么,是否有统计分析方法能够处理以上问题呢?
Almond等(2015)针对教育评估中证据推理的复杂性(complexity)、不确定性(uncertainty)与动态性(dynamic)问题,提出采用基于概率推理的贝叶斯网络(Bayesian network)方法。概率无处不在,它允许我们从不确定和不完整的数据证据中做出复杂的统计推论。对于多维度、多层次的教育数据,变量间的关系错综复杂,概率推理计算困难。例如在评估学生英语的听说读写能力时,写作与听力水平依赖于阅读能力,但是又影响着口语能力。同时,英语能力也受到学生沟通交流能力的影响,所以要评估或预测学生的听力水平必须考虑其他能力的高低。一种简单的处理方法是画出变量关系的网络图(如图1所示),网络图中的节点(node)表示变量,其连线(edge)表示变量间的依赖关系,箭头指出的变量为“原因”变量,箭头指向的变量为“结果”变量。这类网络模型反映了变量间的因果关系,并能够以贝叶斯的方式(即随着新数据的收集而更新)表示复杂且不断变化的信息状态。图灵奖获得者Judea Pearl(1988)推广了这类网络模型,并称之为贝叶斯网络。

图1 贝叶斯网络示例(Almond等, 2015)
贝叶斯网络使用图形表达变量间的复杂关系(图1),变量关系既可以根据理论设定,也可以由数据信息给出。从这一点来说,贝叶斯网络模型同教育与心理学实证数据分析常用的路径分析模型与结构方程模型(侯杰泰等, 2004)十分相似。然而贝叶斯网络和其他使用类似图形结构的模型之间存在几点区别。首先,贝叶斯网络无需假定变量间的线性关系,特别适用类别变量的非线性关系建模(Gupta &Kim, 2008)。其次,贝叶斯网络依据概率来报告变量状态,适合诊断与预测(Sinharay, 2006)。更重要的是,贝叶斯网络能够随着数据的收集而更新(Reichenberg, 2018),这意味着,数据证据可以积累或改变。研究者可以得到更多的数据证据支持研究理论,也可能有新的数据证据反对研究理论。数据证据的更新不依赖于实验设计,模型中任意变量数值的改变都将对整个模型产生影响。
目前贝叶斯网络已广泛应用于各个研究领域,包括计算机科学、统计学、认知科学、心理学、教育学等。在教育学领域,贝叶斯网络的应用主要涉及:(1)学生发展的动态监测,García等(2007)使用贝叶斯网络诊断并监测学生的学习风格;Carmona等(2008)设计动态贝叶斯网络构建学生学习风格模型;Sabourin等(2013)利用动态贝叶斯网络构建自主学习的早期预测模型。(2)不同维度的数据证据整合,Belland等(2017)将贝叶斯网络用于STEM教育中的认知数据证据整合;De Klerk等(2015)利用贝叶斯网络对教育心理学数据测量做了系统性评估。(3)复杂研究问题的模型构建,Pietro等(2015)在高等教育研究中使用贝叶斯网络评估教师表现,同时考虑内部绩效指标以及学生需求、期望、满意度等外部指标;Xenos (2004)在开放与远程教育中使用贝叶斯网络评价学生表现,构建了多变量关系的复杂模型;Mouri等(2016)使用贝叶斯网络预测大学生学业成绩。(4)在教育与心理测量领域的应用,Reichenberg (2018)综述了教育与心理测量中使用贝叶斯网络的文献,并关注其应用;Almond等(2015)展望了贝叶斯网络在教育测评中的应用。在国内的教育实证研究中,同样出现了许多贝叶斯网络的应用研究,主要集中在教育评价(张晓勇等, 2012; 柳炳祥等, 2018; 张戈辉, 2018),认知诊断与自适应学习(宋丽红, 2016; 闫志勇等, 2002)等领域。但是,目前还未见有文章从教育实证研究的角度介绍贝叶斯网络的方法与应用,也未见有研究系统地论述贝叶斯网络方法与模型在教育实证研究中的特征与优势。
本文论述教育数据分析的贝叶斯网络方法与模型,阐述贝叶斯网络与传统实证研究方法在研究范式、数据分析、统计模型等方面的不同与优势,介绍贝叶斯网络的基本算法与实现软件,结合具体的教育实证研究案例展示贝叶斯网络方法的应用。
二、什么是贝叶斯网络
贝叶斯网络是一种以概率方式描述变量之间关系的图模型(Pinto等, 2009),由有向无环图(directed acyclic graph, DAG)和条件概率表(conditional probability table, CPT)两部分组成。其中DAG中的节点表示变量,节点间的有向连线表示变量间的因果关系。若两个节点间以一个单箭头连接在一起,则箭头指出的是父节点(parent node),表示“原因”;箭头指向的是子节点(child node),表示“结果”。例如图1中,阅读指向写作,因此阅读为写作的父节点,写作为阅读的子节点。
贝叶斯网络使用条件概率表储存所有节点在其父节点下的条件概率,若无任何父节点则储存其边缘概率(即不依赖于其他节点变量的概率)。需要注意的是,任意一个变量在给定父节点的情况下都独立于它的非子节点,这有助于变量的评估与预测。例如在图1英语测试中,给定阅读能力时,听力与写作能力是独立的,在评估写作能力时,我们仅需考虑写作在阅读和交流能力下的条件概率。根据贝叶斯网络的链式法则,所有变量的联合概率分布可以简化为每个节点关于其父节点的条件概率的乘积。每个节点的边缘概率等于每个节点的条件概率乘以其父节点的条件概率直至最上方的父节点的边缘概率(即最终的“原因”)。以英语能力测试为例,将测试结果简化为两个状态:高分或低分(记为1或0),图2展示了其中交流、写作、阅读三个能力变量间的网络结构模型。用P(写作)表示写作得高分的概率,P(阅读)表示阅读得高分的概率,P(交流)表示交流得高分的概率。此外,交流是阅读的父节点,交流得高分的学生在阅读上能得高分的概率表示为P(阅读|交流)。同样地,交流和阅读都得高分的学生在写作上能得高分的概率表示为P(写作|阅读,交流)。那么,可以从图中变量间的依赖关系推出P(阅读)=P(阅读|交流)×P(交流)以及P(写作)=P(写作|阅读,交流)×P(阅读|交流)×P(交流)。在收集到学生三项能力测验表现后,可得交流能力的边缘概率并计算出阅读、写作能力的条件概率表,建立完整的贝叶斯网络模型。
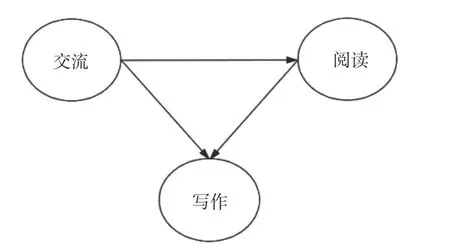
图2 贝叶斯网络推理示例
贝叶斯网络可以进行因果推理(causal inference),目标变量在给定其他变量状态时的概率作为推理依据。具体地,目标变量及其父节点、子节点和子节点的其他父节点共同组成了该变量的马尔可夫毯(Markov Blanket),提供所有的概率依赖信息。利用这些概率信息,贝叶斯网络可以实现从原因到结果的推理,从结果到原因的推理,同一结果不同原因的关联推理,以及包含以上三种的混合推理等。在英语测试的例子中,当数据更新学生交流和阅读的表现后,可预测其写作能力高的概率(原因到结果);当知道学生的写作和阅读表现后,可反推其交流能力高的概率(从结果到原因);当知道学生的写作表现后,可推理交流和阅读的关系(关联推理)。对因果推理感兴趣的读者可参考Pearl(2009)。
贝叶斯网络结构中的变量依赖或独立关系可以从图的角度进一步讨论。在网络图DAG中,d分离(d-separation)提供了一种方法快速确定任意一对变量之间是否条件独立(Pearl, 1988; Geiger, Verma& Pearl, 1990)。考虑三个节点A,B和C,A和B通过C间接连接的情况有三种:汇连(converging connection)、顺连(serial connection)、分连(diverging connection),如图3所示。汇连结构也被称为V结构,变量C能够诱发A和B之间的信息流动,A和B之间边缘独立,但以C为条件时,A和B之间条件依赖。这种结构类似回归模型,如家庭环境A与学校环境B共同影响学生行为C,家庭环境和学校环境边缘独立,但当考虑学生因素时,条件依赖。在顺连和分连结构中,变量C将阻塞A和B之间的信息流动,A和B之间边缘依赖,但以C为条件时,A和B之间条件独立。顺连结构类似中介模型,如家庭社会经济地位A通过子女社会文化观C间接影响子女的创造力B,家庭社会经济地位与子女创造力相关,但在子女社会文化观不变时,家庭社会经济地位和子女创造力条件独立。分连结构又称为共同原因模型,如教育双减政策C提升了教师满意度A与家长满意度B。

图3 节点之间的三种基本结构
三、贝叶斯网络能为教育实证研究带来什么?
前文介绍了贝叶斯网络模型与方法,本节具体讨论贝叶斯网络相较于传统方法的优势,能解决哪些传统方法不能解决或不能很好解决的问题。
(一)理论驱动与数据驱动的融合
随着人工智能、大数据分析的发展,国内外研究者开始关注数据驱动的教育学研究(Kurilovas,2020; 孟志远等, 2017; 杨现民等; 2020),但也有学者重申理论驱动的教育研究的重要性(Huang & Hew,2018; 杨向东, 2014)。理论驱动的分析流程是“研究问题—提出假设—设计实验—收集分析数据—验证假设”,研究者需要理论构建模型,表达变量间的关系。数据驱动的分析流程是“研究问题—收集分析数据—得出结论”,研究者直接根据获得的所有数据信息构建模型,省去了研究假设与实验设计。
下面以农村地区学生学业困难的影响因素为例(Mandinach, 2012),具体说明两种传统分析路径的差异与缺点,并阐述融合理论与数据驱动的贝叶斯网络方法的优点。理论驱动分析方法首先根据研究问题提出研究假设,影响学业困难的因素有家庭状况、健康状况、不良行为等。再确定抽样对象、样本容量及观测变量,包括因变量学习成绩,自变量家庭收入、医疗记录、违纪频率等。随后收集数据,使用线性回归模型分析以上自变量是否对学习成绩有显著的影响及影响大小,验证研究假设。这一分析流程存在两个缺陷。首先,理论假设可能忽略某些对学业困难有显著影响的重要变量,如班主任管教方式,一旦确定研究设计、收集数据后无法增加新的观测变量。其次,需要事先设定样本容量的大小,样本不足会导致假设检验失效,而样本过多则会提高实验成本。
数据驱动分析流程首先明确研究问题,研究者试图了解为什么部分学生会在学业上遇到困难。随后收集到学生学业成绩、医疗记录、行为数据、出勤率等,以及其他看似与学业困难不相关的变量,如当地交通、当地气候等。基于所有数据信息,利用相关分析、聚类分析等大数据分析常用方法,得到学业困难的相关因素。注意,所有观测到的数据信息都可以加入分析。数据驱动方法的缺点是仅能判断与学业困难相关的变量,无法解释它们的影响机制。如研究者发现学生学业困难与当地气候有关,但真实原因可能是恶劣天气导致交通不便,进而影响学生学业。
贝叶斯网络结合理论驱动与数据驱动的思想,其基本分析流程可归纳为:“研究问题—先验模型—收集分析数据—阶段性结论—更新模型—收集分析数据—”。首先,贝叶斯网络可以整合特定教育研究领域内的理论知识与专家经验。贝叶斯方法鼓励专家(教育学者、一线教师等)参与选取变量并定义变量间的关系,这种关系可以是相关也可以是因果。比如,指定当地气候影响交通,进而影响学业困难的路径。专家经验将作为先验知识加入贝叶斯网络模型,这意味着先验模型的结构将有教育理论支撑,也能适应特定的研究目的。其次,在先验模型构建之后,研究者收集分析数据,得到阶段性结论,并更新先验模型,再收集分析数据,以此迭代。基于这一流程,贝叶斯网络能够从教育数据中学习。贝叶斯网络的数据学习特性来源于贝叶斯公式,其反映了人们对过去的认知会随着新数据的加入而发生改变。当收集到新的数据时,贝叶斯网络将改进基于教育理论或专家经验的原始模型,或更新之前数据分析得到的历史模型。这种学习既可以调整模型参数,也可以对模型结构提出更改建议。后者对于教育研究是有指导意义的,因为它反映了不断积累的数据证据对教育理论或专家经验的批判性修正。比如,随着小康社会的全面建成、农村经济的整体发展,家庭收入、交通状况或不再是影响学业困难的主要因素,而学业压力等可能成为新的影响因素。因此,新研究数据的分析结果会动摇我们对过去的认知。需要注意的是,部分数据分析结果往往不足以推翻旧的理论,但是贝叶斯模型会降低历史模型的可信度,直到积累足够的数据证据反对历史模型。
综上,相较于传统理论驱动或数据驱动分析方法,贝叶斯网络融合理论与数据信息构建模型,随着新数据的收集迭代模型,更新研究结论。贝叶斯网络方法避免了理论驱动方法在假设模型提出后无法增加新的变量,在实验设计后无法增加样本容量,在得到结论后无法更新修正等问题;同时,贝叶斯网络方法弥补了数据驱动方法在解释变量因果关系、影响机制等方面的不足。
(二)概率推理
基于概率推理的教育实证研究结果具有不确定性,这种不确定性来自研究抽样误差、测量误差、统计分析误差等。传统统计推断报告的研究结论通常是变量存在“显著差异”“显著相关”“显著影响”等,研究者无法知晓其所关心变量,如学生能力、教师水平等高低的概率。贝叶斯网络将概率推理的不确定性纳入模型。概率可以用来表示个体发展、预测信息、情景感知以及数据和先验知识融合等不确定性。研究者根据理论设定贝叶斯网络初始模型时,将这些不确定性带入模型,当数据输入后,利用概率迭代进行推理,推理的结论同样以概率表示。
以网络教学中的学生学习风格推理为例(García等, 2007),学习风格包括信息加工、感知、输入和理解等维度。其中,信息加工有两种类型:活跃型与沉思型,根据学生在网络学习论坛和聊天室中的不同行为表现推理其信息加工的类型。论坛变量包括四种状态:回复消息、阅读消息、发布消息、不参与;聊天变量包括三种状态:参与、聆听、缺席。研究者评估学生信息加工风格,对于类别变量的关系,传统统计方法常使用交叉表格卡方检验,但是其得到的结论只能是信息加工风格与论坛、聊天等变量独立或显著相关;或是使用二元逻辑回归模型,但是其只能判断论坛、聊天等变量是否显著影响信息加工风格。而贝叶斯网络方法除了构建模型表达变量间的关系,还能对学生个体的信息加工风格进行概率推理。比如García等(2007)构建了图4的贝叶斯网络,并根据数据生成变量的条件概率表1。若观测到某学生在论坛回复消息且参与聊天,则由表1可推理其信息加工风格为活跃型的概率为0.85;若观测到另一位学生仅在论坛中阅读消息并且没有参与聊天,则可推理其信息加工风格为沉思型的概率为0.55。与传统统计推断方法得到的变量显著相关、显著影响等结论相比,贝叶斯网络更关注个体层面的概率推理,得到的结论更加精准有效。
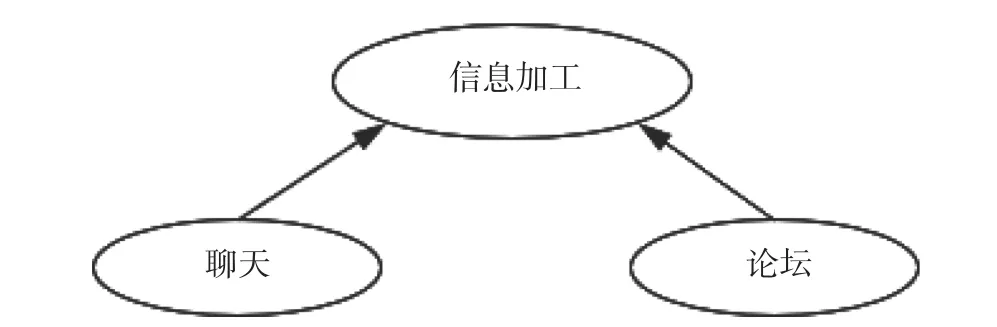
图4 信息加工的贝叶斯网络

表1 信息加工风格条件概率表
(三)复杂模型构建
教育研究问题往往涉及多变量、多维度的复杂建构。为了处理变量间的复杂关系,教育数据分析大多采用中介与调节模型(温忠麟等, 2005)、结构方程模型(侯杰泰等, 2004)、多水平模型(马晓强等,2006)等。但是这些模型都有很强的数据假设,如正态性、模型残差随机、独立、齐次等,在处理类别变量的非线性关系时,会有较大的估计误差,导致模型诊断与预测效果不佳(Gupta & Kim, 2008)。此外,这些模型能够处理的变量关系复杂度有限,拟合具有较高复杂依赖性的数据是一项挑战(Almond等,2015)。贝叶斯网络对数据类型与变量关系类型都没有要求,连续或类别变量、正态或非正态数据都可以纳入贝叶斯网络模型;线性或非线性的变量关系都可以在贝叶斯网络模型中表达与分析。同时,作为大数据分析方法,贝叶斯网络能够处理多维度、多层次的复杂变量关系。
在前文例子中,研究者诊断学生学习风格,考虑信息加工、感知、理解维度(García等, 2007)。每个维度有两种类别,分别为活跃型与沉思型、感悟性与直觉型、序列性与综合型,由学生的网络学习行为数据诊断。研究中的信息加工、感知、理解均为类别变量,不满足传统线性回归模型、中介模型等的正态性、方差齐次、线性等假设。图5构建了学习风格的贝叶斯网络,研究者根据聊天行为、考试提交时间、修改答案行为、考试结果等变量诊断学生个体的学习风格。此外,在图5中贝叶斯网络可将学习风格模型的各维度分块建模,再对学习风格模型整体进行评估,分析信息加工、感知与理解维度间的关系。

图5 学习风格的贝叶斯网络(García等, 2007)
(四)实时监测与反馈
传统教育测评多以纸笔测验为主,计算测验问卷的总分或平均分。这类评估通常指向知识、技能的单一维度,无法进行多维度、多层面的复杂测评。同时,如果问卷包含较多题目,或者学生没有意识到问卷的用途,往往会不经过仔细思考随意选择答案,得到的结果可能是不准确的。此外,传统测评独立于教学与学习活动,强调终结性评价,无法获知学生在学习过程中的发展与变化。当前教育研究关注过程性评价,以真实学习情境为载体,智能设备与系统为工具,教育过程数据为证据,动态测评模型为方法,实时监测与反馈为目标,评估学生在学习过程中体现出来的知识、技能、方法、思维、风格和价值观念等。随着便携式视频设备、智能学习系统引入课堂,学生在教学活动过程中的多维、动态数据可被捕捉,如教师教学时学生的面部表情,小组讨论中学生的发言次数,课堂练习中学生点击智能设备的频率等。基于教育过程数据在真实课堂中评价学生的能力,能够帮助教师全面、即时地了解学生的发展状况,从而更好地建立学习提升计划。
传统动态数据分析方法是建立时序模型,即将变量进行时间分割后加入模型,如重复测量模型、纵向追踪模型、自回归模型、交叉滞后模型(Grimm等, 2021)等。这类模型分割的时间是离散的,需要在某一时刻观测到所有变量数据信息才能更新模型。但是教学与学习过程是连续的,行为数据并非发生在某一特定时刻;换句话说,特定时刻可能观测不到研究者需要的行为信息,因此这类时序模型无法做到实时监测与反馈。贝叶斯方法的天然优势就是处理数据的动态更新。教育研究者根据理论或专家经验等设置初始模型后,每当数据进入,模型都将更新,支持或反对研究理论的数据证据也持续累积。值得注意的是,在某一时刻,贝叶斯网络不需观测模型中的所有变量即可完成更新。例如,在数学课堂学习中,捕捉到学生举手发言后,我们对其注意力、计算思维等能力的评估,以及数学成绩的预测也将随之发生改变。贝叶斯网络能够有效融合动态学习过程中的所有数据信息,从而帮助教师评估学生知识、能力等的薄弱环节,实现实时监测和反馈。此外,贝叶斯网络还能够综合历史数据,推测学生发展趋势,为教师调整教学方案提供参考。
以前文学生学习风格与其在网络教学中的互动行为关系为例(García等, 2007),研究者可以建立重复测量模型,构建学习风格与互动行为的动态关系。例如在学习开始时、中间某时刻、结束时,分别收集学生的聊天、论坛、邮件等行为数据,构建学习风格的重复测量模型,评估学生学习风格在三个时刻的变化趋势。但是,重复测量模型等传统时序模型局限于固定时刻变量关系的多次评估,无法做到学习风格的实时评估。为此,García等(2007)构建了学习风格与互动行为的贝叶斯网络模型,分析学生在使用网络教学系统时的学习与互动过程数据(见图5)。模型构建与数据分析是连续的动态过程,在任意时刻,学生的任何行为,如参与聊天、回复邮件等,都将更新模型,给出学习风格的最新概率推理结果。换句话说,监测学生学习风格不需设置特定时间节点,不需观测所有行为数据。因此,贝叶斯网络相较于传统时序模型,能够提供实时监测。
(五)小样本、缺失与不完整数据分析
受限于人力、物力、经费等实验条件,教育实证研究的样本容量可能相对较小。例如,教育神经科学研究需要对被试进行脑红外成像或核磁共振,能收集到的样本有限。在参数估计方面,对小样本数据使用传统极大似然法(Maximum likelihood)估计变量间的相互关系,极易受到个别极端数据的影响,产生有偏差的估计结果。贝叶斯方法融入基于专家经验或历史数据的先验信息,减小了极端值的影响,比极大似然法的估计精确度更高(Van de Schoot等, 2017)。在假设检验方面,频率统计方法需要确定样本容量、显著性水平等。实际操作中研究者可能会因为样本容量较小,无法得到任何结论,也可能会收集过多的样本数据造成浪费。贝叶斯方法无需预先设定样本容量,不依赖于实验设计,对多次实验可以进行数据证据的积累。即使一次实验的样本较小,无法得到有用的结论,研究者也可以继续收集新的数据,在贝叶斯模型中积累数据支持研究假设的证据,直到得到有意义的教育研究结论。一般来说,贝叶斯统计分析所需的样本容量都小于频率统计分析,而贝叶斯网络继承了贝叶斯统计方法在小样本参数估计和假设检验方面的优势。
教育研究数据可能存在缺失或不完整的情况,例如因为实验设备问题造成的部分学生的视频或音频数据缺失。对于缺失与不完整数据,贝叶斯网络同样比传统方法表现更优。贝叶斯网络模型可根据变量间的相互依赖关系计算各变量的条件概率,比如当学生听力水平高的概率是80%时,即使其口语能力测验数据缺失,我们也可根据其听力水平对口语能力进行估算。在具体分析中,贝叶斯网络使用期望最大化(Expectation-Maximum)算法从不完整数据中估计条件概率。与其他估计方法不同,无论数据是随机缺失或是缺失依赖于其他变量的状态,期望最大化算法都可以处理缺失值的估算。
本节重点阐述了贝叶斯网络方法较传统数据分析方法的优势:融合理论与数据驱动分析思想;能够对个体进行精准概率推理;适用任何数据与变量类型;对变量多维度、多层次的复杂关系进行建模;对教育过程数据进行实时分析与反馈;不依赖样本容量与实验设计等。
四、贝叶斯网络分析算法与软件
由第2节讨论可知,当知道各个变量节点的因果关系后,贝叶斯网络的结构即可确定。但是,如果关于网络结构的先验信息不可知,则需要用数据驱动的方式构建网络图模型,即贝叶斯网络的结构学习。目前贝叶斯网络结构学习算法可分为三类:基于约束的算法(constraint-based algorithm),基于评分的算法(score-based algorithm)以及两者的混合算法。基于约束的算法主要使用条件独立性检验来识别变量之间的条件独立关系,并构造相应网络结构图(De Campos & Huete, 2000),其优点是便于判断变量间的因果关系,但是计算较为复杂。基于评分的算法使用评分函数衡量网络模型与数据的拟合程度,将结构学习视为一个结构优化问题,利用搜索策略来选择评分最高的结构。广泛使用的评分指标包括模型比较常用的AIC和BIC信息准则分数。评分搜索算法的优点是给出了模型拟合数据的程度,但是当变量节点较多时,无法遍历所有可能的模型,容易陷入局部最优。在确定结构模型后,贝叶斯网络分析的任务是计算条件概率表,即贝叶斯网络的参数学习。参数学习主要有极大似然估计和贝叶斯后验估计两种方法。这里推荐贝叶斯估计方法,与贝叶斯网络的整体分析方法(即贝叶斯法)具有一致性,并且贝叶斯方法对于小样本数据有较好的参数估计精度。
能够实现贝叶斯网络数据分析的软件非常之多(Scanagatta et al, 2019),这里仅介绍基于不同平台的部分软件,并对其算法、功能等进行比较,详见表2。基于R语言平台的bnlearn (Scutari, 2009)是目前使用最广泛的贝叶斯网络软件,其功能强大,适用各种数据类型和结构学习算法,并能构建动态贝叶斯网络模型,进行参数估计、模型比较和近似推理等。其他两个R软件包Deal和pcalg分别采用基于评分和基于约束的结构学习算法,但是均不能构建动态贝叶斯网络模型。Banjo和Free-BN适合Java软件使用者,BNFinder适合熟悉Python软件的研究者,BNT适合熟悉Matlab软件的研究者。

表2 贝叶斯网络常用软件
五、贝叶斯网络的实证研究应用
本节使用一个教育实证研究案例来展示如何构建、分析和报告贝叶斯网络。该实例关注青少年在合作学习过程中展现的尊重、帮助、关心、同情等亲社会行为与同伴关系发生和发展的作用机制(陈森宇等, 2021)。研究收集了22名来自河北省某县级中学的七年级学生的课堂合作学习行为视频数据,其中男生8名,女生14名。这些学生被分为3个小组(7+7+8=22)参与基于合作推理讨论(Anderson et al, 1998)的合作学习模式,每个小组进行8轮讨论,其中第一次讨论为正式讨论前的“预演”,便于学生熟悉合作推理讨论的规则和形式,之后的7轮讨论作为观察数据进行同伴互助行为的编码,共计21次讨论,讨论平均时长27.5分钟。
学生的互助行为包含讨论促进行为、行为支持、认知支持、情感支持等四个大类别。其中,讨论促进行为包括邀请他人发言,提醒讨论规则,进一步指导等小类;行为支持表示直接回应组员的需求,提供相关学习资源等小类;认知支持包括为组员提供解释、建议、指导,补充、评论、澄清对方观点等小类;情感支持包括对组员给予安慰、鼓励、关心,表达理解、尊重、亲近等小类。研究在讨论前与讨论后测试了学生的同伴喜欢程度和同伴关系提名,前者需要学生指出是否喜欢和组内某同学一起玩(0表示不认识,1表示不喜欢,2表示喜欢),后者需要学生指出组内哪些成员被认为是他/她的好朋友(0表示不是,1表示是)。表3展示了在7轮讨论中,四类互助行为出现的次数以及同伴喜欢程度和同伴关系提名次数。其中,讨论促进行为在初期较多,随着讨论的进行,讨论促进行为逐渐减少。行为支持略有上升,而认知支持和情感支持的变化不大。同伴关系提名次数明显增加,同伴喜欢程度明显上升。以上分析描述了学生互助行为与同伴关系变量的独立变化。

表3 学生互助行为与同伴关系统计描述表
传统回归分析方法的分析思路是构建因变量为同伴喜欢程度或同伴关系提名,自变量为讨论促进、行为支持、认知支持、情感支持等的线性回归模型,当模型设定后,可在T2、T3等时刻随着讨论的进行预测同伴喜欢程度或同伴关系提名的变化。但是,同伴喜欢程度或同伴关系提名在理论上是互助行为发生的内在原因,学生更有可能帮助或支持和自己关系好的组内同学。在交往和互助的过程中,具有相同或相近社会认知能力的学生更有可能发展友谊关系。因此,以同伴喜欢程度或同伴关系提名为因变量的回归分析是不合适的。此外,该研究涉及类别变量,类别变量的数据分析是对变量发生概率的解释和预测。使用线性回归或逻辑回归模型需要对类别变量进行虚拟化处理(dummy coding),其结果的解释较为复杂。最后,本研究的初始样本容量较小,传统分析方法可能无法得到任何有用的结论,也不能随着新数据的输入而更新数据证据。
本研究利用贝叶斯网络构建互助行为与同伴喜欢程度和同伴关系提名的模型。为了演示简便,模型只包含四个大类互助行为与同伴喜欢程度和同伴关系提名。在T1时刻,可获得所有变量的观测数据,根据先验理论构建如图6中T1时刻所示的贝叶斯网络模型。图6中的变量名下方展示了各变量的边缘概率,例如T1时刻,同伴关系提名与否的概率分别为8%和92%,同伴喜欢程度高的概率为12%,低的概率为49%,不认识的概率为39%等。当理论模型不确定时,可计算各个备选模型的评分指标(如AIC、BIC等)进行模型比较,选择最优的先验模型。确定模型并带入数据后,即可生成条件概率表,如表4所示。
在表4中,P(同伴关系提名)所在行显示了同伴关系提名为0和1的概率。在图6模型中,同伴关系为最上方的父节点(即最终的“因”),因此该概率为不依赖于其他变量的边缘概率,与图6中T1时刻同伴关系下方的概率相同。P(同伴喜爱程度)所在行展示了同伴喜欢程度为0、1、2的概率,该概率为依赖于同伴关系提名的条件概率。例如当同伴关系提名为1时,同伴喜欢程度为2的条件概率为0.884。P(讨论促进)等其余行给出了四个互助行为在同伴关系提名和同伴喜欢程度给定下的条件概率。例如同伴关系提名为0且同伴喜欢程度为1时,可得认知支持为1的概率为0.544。此外,当同伴关系提名为1且同伴喜欢程度为0时,互助行为的条件概率都为默认概率0.5,这是因为该情况没有任何观测数据,学生提名的好朋友不会是他或她不认识的同学。
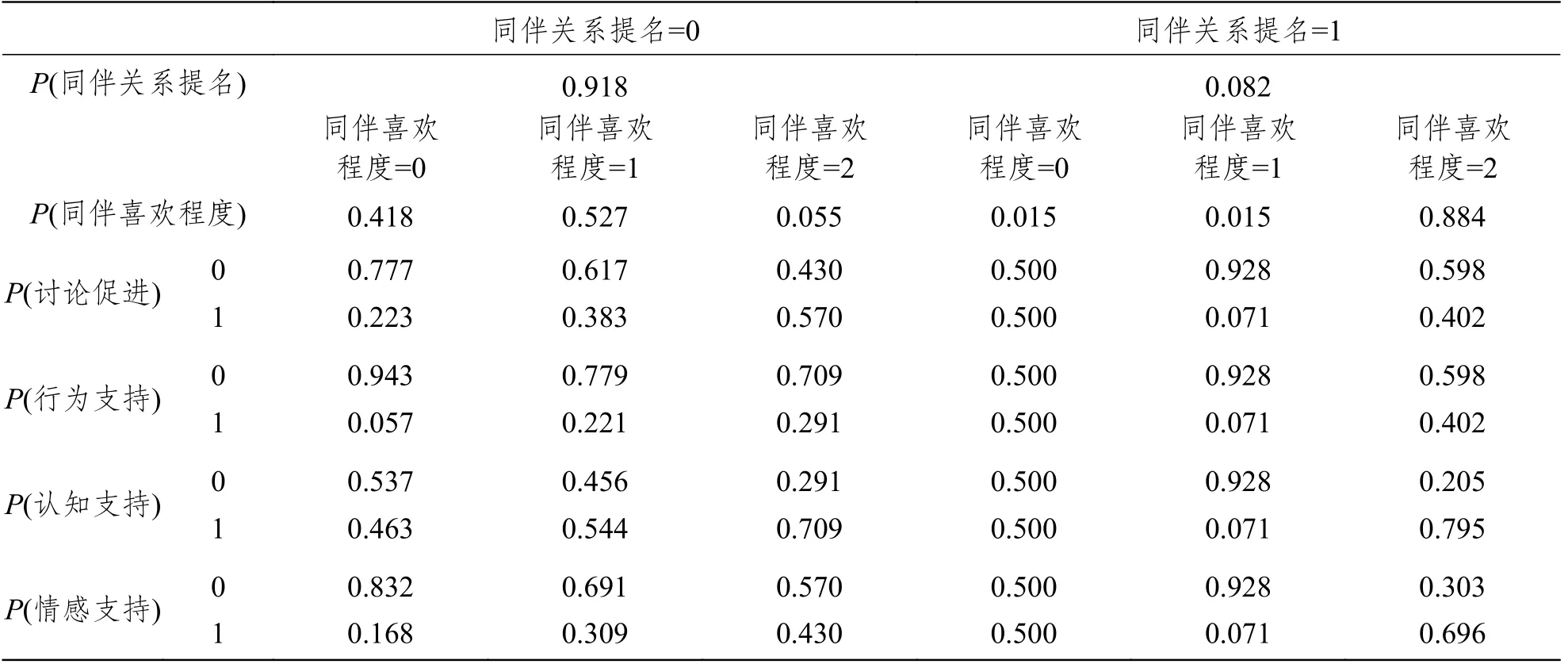
表4 T1时刻贝叶斯网络模型条件概率表
T2到T6时刻仅能观测学生的互助行为,但是可以利用贝叶斯网络和条件概率表预测同伴喜欢程度与同伴关系提名。图6中的T3和T5网络图为合作学习小组讨论中选取的两个时刻的预测模型,其中互助行为下方的概率为观测值,同伴喜欢程度与同伴关系提名的概率为预测值。在T7时刻讨论结束后,对学生的同伴喜欢程度与同伴关系提名再一次进行测试,新的数据用于更新模型,更新后的模型如图6中的T7网络图所示,条件概率表见表5。

表5 T7时刻贝叶斯网络模型条件概率表

图6 同伴关系与互助行为的贝叶斯网络图
当研究者没有任何先验知识时,可使用完全数据驱动的结构学习算法构建贝叶斯网络模型。图7展示了同伴喜欢程度和同伴关系提名与11个学生具体互助行为在T1时刻的网络关系,与所有变量都无关的互助行为已被删除。需要注意的是,完全数据驱动的模型可能无法解释或错误解释变量间的关系,如图7中的很多互助行为并不存在因果关系,如实物帮助与给予提醒、补充评论观点与提醒讨论规则等。当新的数据不断进入模型后,变量的关系可能会被修正,条件概率表将会更新。多次数据迭代更新后的贝叶斯网络模型能够准确推断、预测变量的变化。
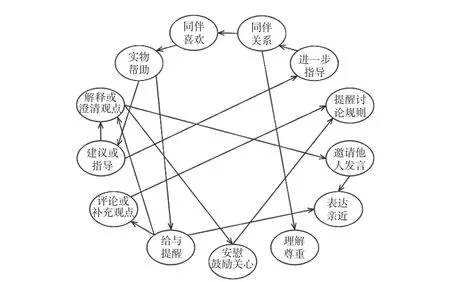
图7 数据驱动的同伴关系与互助行为贝叶斯网络图
六、总结
本文阐述了贝叶斯网络法在教育实证研究范式、数据分析方法、模型应用等方面的优势,讨论了贝叶斯网络模型的特征、算法与软件,通过教育研究实例展示了贝叶斯网络模型数据分析过程。贝叶斯网络方法已广泛应用于众多研究领域,但在教育实证研究中的应用相对少见。可能的原因是教育大数据研究尚处于起步阶段(孟志远等, 2017),作为大数据分析方法的贝叶斯网络未被教育研究者所熟知。为此,本文呈现了贝叶斯网络的基本方法与分析流程,旨在推广贝叶斯网络在教育实证研究中的应用。

