基于数据增强的运动想象脑电分类
彭禹,宋耀莲,杨俊
基于数据增强的运动想象脑电分类
彭禹,宋耀莲*,杨俊
(昆明理工大学 信息工程与自动化学院,昆明 650500)(∗通信作者电子邮箱39217149@qq.com)
针对运动想象脑电(MI‑EEG)多分类问题,在已有研究的基础上进行改进,构建了基于深度可分离卷积的轻量级卷积神经网络(L‑Net)和轻量级混合网络(LH‑Net),并在BCI竞赛Ⅳ-2a四分类数据集上进行了实验和分析,结果表明:L‑Net比LH‑Net可以更快地拟合数据,训练时间更短;但LH‑Net的稳定性比L‑Net更好,在测试集上的分类性能具有更好的稳健性,平均准确率和平均Kappa系数比L‑Net分别提高了3.6个百分点和4.8个百分点。为了进一步提升模型分类性能,采用了基于时频域的高斯噪声添加新方法对训练样本进行数据增强(DA),并针对噪声的强度进行了仿真验证,推测出了两种模型的最优噪声强度的取值范围。仿真结果表明使用了该数据增强方法后,两种模型的平均准确率最少提高了4个百分点,四分类效果均得到了明显提升。
脑电信号;运动想象;深度学习;深度可分离卷积;数据增强
0 引言
脑机接口(Brain‑Computer Interface, BCI)在人类大脑和外部设备之间提供了一种新的人机交流模式,通过它可以将人脑中的想法编码成计算机可以识别的机器指令进一步控制外接设备运作[1]。在不同类型的脑电(ElectroEncephaloGraphy, EEG)信号中,运动想象脑电信号(Motor‑Imagery EEG, MI‑EEG)[2-3]近年来引起了广泛的研究,目前研究人员已经使用MI‑EEG信号帮助中风和癫痫患者交流[4-5]、控制轮椅和机器人等外部设备,甚至用于阿尔茨海默病等疾病的研究[6]。但是EEG信号由于受采集环境、设备以及受试者的身心状态的影响,具有高度的非平稳性和信噪比低的特点,增加了EEG分类任务的难度[7]。
1 相关工作
传统的机器学习方法虽然在EEG分类方面取得了一定的成功,但仍不能达到良好的解码精度。目前深度学习方法的成功推动了研究人员将其应用于EEG信号分类,深度学习证明了EEG特征自动提取可以达到更好的效果[8]。Lawhern等[9]针对来自不同BCI范式的EEG信号提出了一种紧凑型的模型EEGNet,在目前较常用的四种BCI范式上表现出了良好的性能;Sakhavi等[10]基于滤波器组通用空间模式(Filter Bank Common Spatial Pattern, FBCSP)方法将EEG转换成一种新的时间包络表示,并使用卷积神经网络(Convolutional Neural Network, CNN)进行分类,在BCI竞赛Ⅳ数据集2a上平均准确率达到74.46%;Amin等[11]提出了多层CNN融合模型,该模型将多个不同深度的CNN提取到的特征分别通过多层感知器(Multi‑Layer Perceptron, MLP)和自编码器进行特征融合;杜秀丽等[12]提出了一种融合注意力模块的CNN模型,通过注意力模块增强重要特征信息、抑制不重要特征的方式有效提升了模型的分类性能,该模型在BCI竞赛Ⅳ‑2A数据集上平均准确率达到了81.6%。包括以上分类方法在内,目前大多数深度学习的模型都是在EEG的预处理,或者是在模型输入形式上做了较多的特征处理工作,这很可能导致原始EEG信号中有效信息的丢失[13],致使网络模型分类表现欠佳。
针对以上问题,本文参考了EEGNet[9]的特点,构建了两种不同结构的轻量级网络:L‑Net(Lightweight Convolutional Neural Network)和LH‑Net(Lightweight Hybrid Network);同时提出了基于短时傅里叶变换(Short‑Time Fourier Transform, STFT)的高斯噪声添加方式来扩充数据。为了验证两种模型以及基于STFT的数据增强方式的性能,在BCI竞赛Ⅳ中2a数据集进行模型训练、测试和评价。
2 本文方法与原理
2.1 基于深度可分离卷积的分类方法
考虑到数据集规模较小的特点以及硬件设备的限制,本文设计了两种网络参数体量较小的轻量级网络模型,分别为L‑Net和LH‑Net,二者的具体网络结构分别如图1、2所示。在模型的输入表示上,本文将EEG信号的通道数量作为输入样本尺寸的高度,将采样点的数量作为样本的宽度。这种将输入表示为二维矩阵的形式,与将EEG信号转化成时频图片的方式[16]相比,优势在于能显著降低输入的维数。

图1 L‑Net模型结构

图2 LH‑Net模型结构
L‑Net根据网络层的不同功能主要可划分为三个模块:
1)时空卷积模块,对应图1中的二维的卷积和深度卷积,这两个子层分别对经过时间裁剪后的EEG信号进行时间域和空间域卷积[9]。二维卷积的卷积核的大小为64×1,输出特征图数量为F1即该层卷积核的数量。深度卷积的卷积核大小为1×22,输出特征图数量为F2。
2)深度可分离卷积模块,分别对上一层输出的所有特征图按照通道顺序做深度卷积,再进行逐点卷积。它将标准卷积操作分成了两步,不仅减少了通道之间的耦合,还进一步减少了模型的参数量,输出的特征图数量仍然与上一层保持一致。
3)分类模块,由一维卷积层、展平层和全连接层组成。一维卷积的卷积核大小为4,采用因果卷积来提取更加抽象的EEG特征,卷积之后向展平层输入16个长度为17的特征向量;展平层则将所有向量连接展平为长度为16×17的特征向量,输入到最后的全连接层,并通过Softmax激活函数输出分类概率;全连接层共包含了4个神经元,分别代表网络的4类输出结果(左手、右手、舌头和双脚),该层根据式(1)将输入的特征向量通过一个权重矩阵进行加权求和。
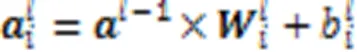
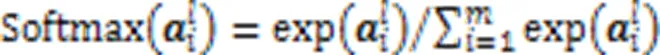
有大量证据表明,EEG信号是跨多个时间尺度组成的,具有较好的时间分辨率[18];而且在深度可分离卷积之后,特征图仍包含了时间信息。因此,为了进一步在更深层次中提取关于EEG更为抽象的时间特征,增强模型的分类效果,本文在L‑Net的基础上,使用图3(b)所示的残差块来堆叠时间卷积网络(Temporal Convolutional Network, TCN),构建了LH‑Net。TCN是Bai等[19]于2018年提出的,且在多个数据集上的表现均比经典的序列模型如长短期记忆(Long Short‑Time Memory, LSTM)网络和门控循环单元(Gated Recurrent Unit, GRU)等更优秀,避免了序列模型经常出现的梯度爆炸、梯度消失等问题。TCN模型的结构特点是它在卷积层使用了因果卷积和膨胀卷积[20],同时加入了残差结构。图3(a)展示的便是TCN的核心模块,它在卷积后面均添加了归一化层、非线性层和Dropout层[19]。LH‑Net也使用了与TCN残差块相同的结构,但是在归一化层上将权重归一化换成了批量归一化,激活函数由修正线性单元(Rectified Linear Unit, ReLU)换成了ELU。LH‑Net在TCN模块之后,将输出的特征矩阵输入到网络的自定义层,并在该层实现了对特征矩阵进行跨通道的特征融合,最后输入到包含四个输出单元的全连接层,并通过Softmax激活函数输出分类结果。
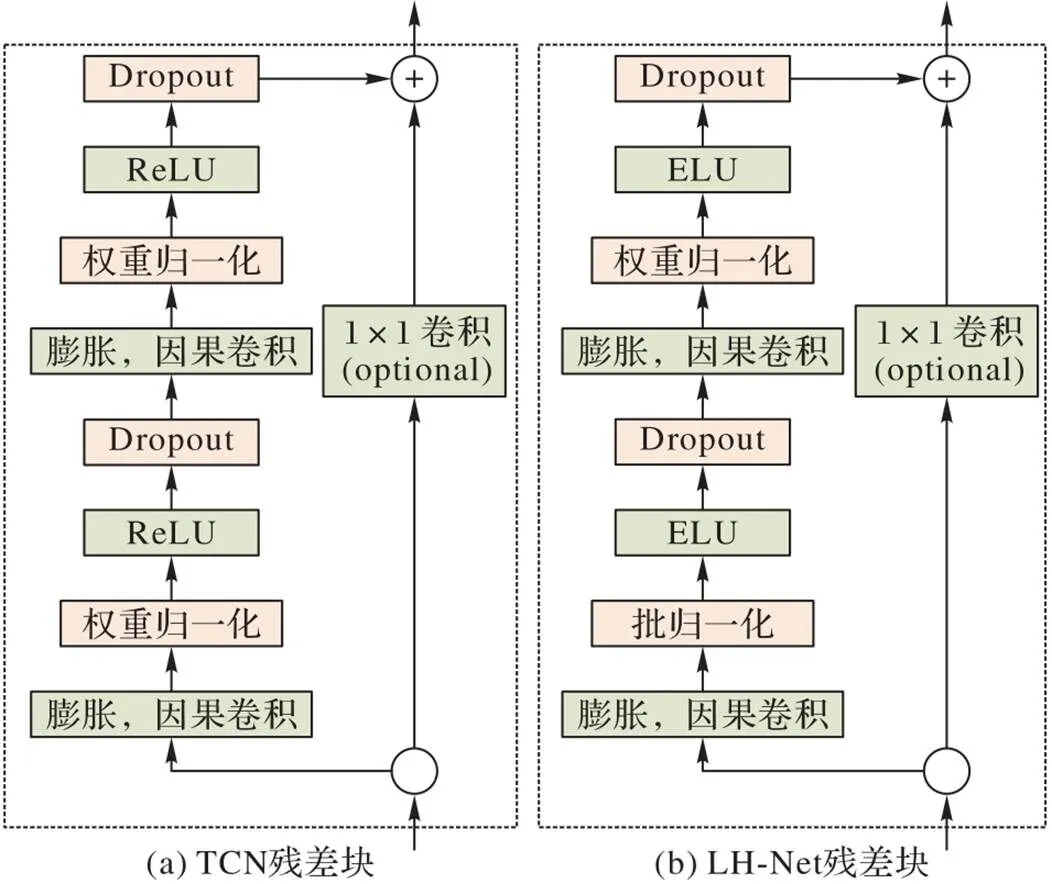
图3 时间卷积网络残差块
2.2 基于时频域的数据增强方法
深度学习模型的分类性能非常依赖于参与模型训练的数据量,尤其在网络深度不断增加的情况下,极大概率会出现过度拟合的问题[21]。在图像处理等领域,解决过拟合的最好方法就是增加训练样本的数量,一般会对图像进行几何变换或者噪声添加。如果对EEG信号进行同样的几何变换,会破坏数据的时域特征;如果直接在EEG信号中加入噪声会破坏信号的幅值和相位信息,从而降低分类精度[14]。综上分析,本文提供了基于STFT的噪声添加方法来扩充训练用的样本数量。同时考虑到EEG信号具有很强的随机性和非平稳性,随机加入一些局部噪声,如泊松噪声、椒盐噪声,会局部改变EEG的有效特征[14],因此,本文使用了高斯噪声来进行噪声添加,具体的算法流程如图4所示。
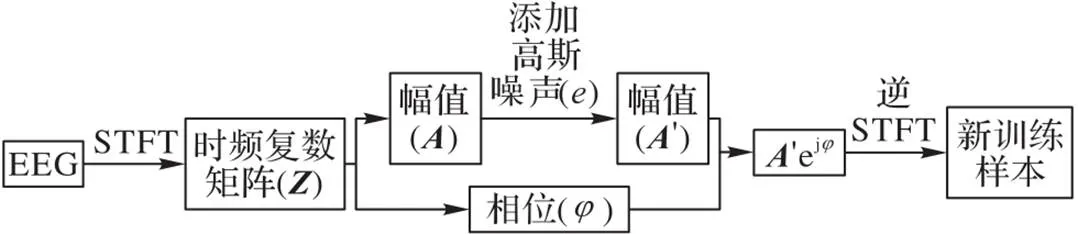
图4 基于时频域的数据增强算法流程
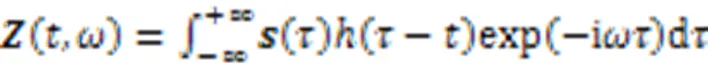
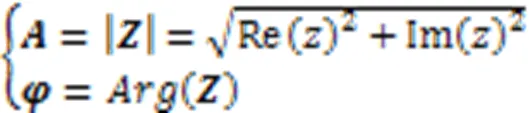
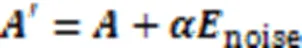

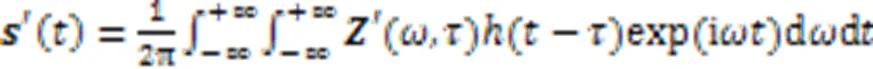
高斯噪声是指它的概率密度函数服从高斯分布的一类噪声。式(8)是关于高斯随机变量的概率密度函数表达式:
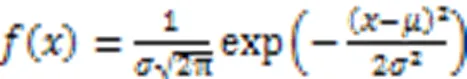
3 实验数据与设置
3.1 数据集和预处理
本文使用的EEG数据来自BCI竞赛Ⅳ-2a数据集,该数据集由奥地利格拉茨工业大学[22]提供。该数据集一共记录了9名受试者关于左手、右手、双脚和舌头四种不同的运动想象任务的EEG脑电信号。每个受试者的数据由两个部分组成:一部分用于训练,另一部分用于测试。每个部分都包含了288次实验,每次实验持续7.5 s,并根据图5所示的计时方案来进行记录。所有数据均是通过分布在头部的22个Ag/AgCl电极记录,采样频率为250 Hz,并且对采集的信号进行了0.5~100 Hz带通滤波。
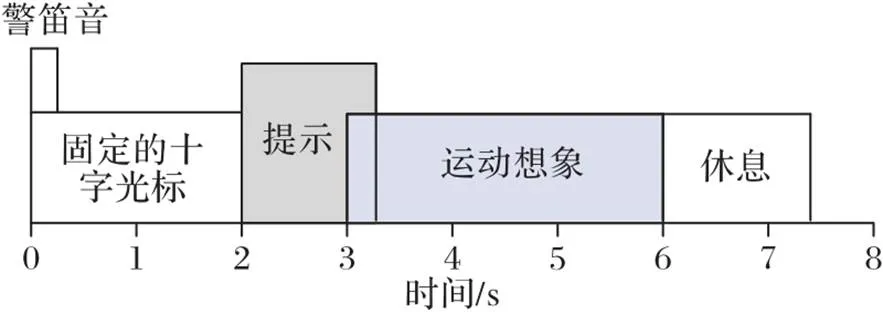
图5 数据采集计时方案
本文首先对原始的EEG信号进行相关运动想象事件段的提取,从每个试次中提示出现的前0.5 s到3 s的运动想象实验结束为止。从图5中来看,即Cue的前0.5 s一直到第6 s运动想象结束,共4.5 s的时间长度。同时本文将提取到的样本标签进行独热编码,用一个长度为4的二进制向量来表示四种类别标签,最后左手、右手、双脚和舌头四类标签分别被编码为1000、0100、0010和0001。MI‑EEG在采集中很容易受到生理性和非生理性的噪声影响,这些被记录的噪声便是伪影。非生理性伪影多数为操作不当引起的,生理性伪影主要由眼部的活动、肌肉活动、呼吸以及汗水等引起。非生理性的伪影可以通过肉眼辨别出,但多数生理性伪影与MI‑EEG的有效频段重合难以剔除,为了尽量减少有效信息的损失,本文未进一步对提取到的数据段进行滤波。
3.2 实验设置
EEG信号中含多个频率分量,且汉宁窗对非平稳信号的良好性能,可以防止频谱泄漏同时消去高频干扰[23]。因此本文在对EEG信号进行STFT时使用汉宁窗作为窗函数,同时为了获得较高的频率分辨率,将时间窗函数的长度设置为256。进行数据增强后,每个类别的训练样本量均扩充为原来的两倍。
图6展示了某个受试者同一个通道上,关于左手和右手两个类别的EEG信号在进行数据增强前后的时频幅值对比。从图6中可以发现,在时频域对训练样本进行噪声添加后,很好地保留了信号的时频特征,同时在局部的特征上有比较明显的区别,达到了本文数据增强的目的。
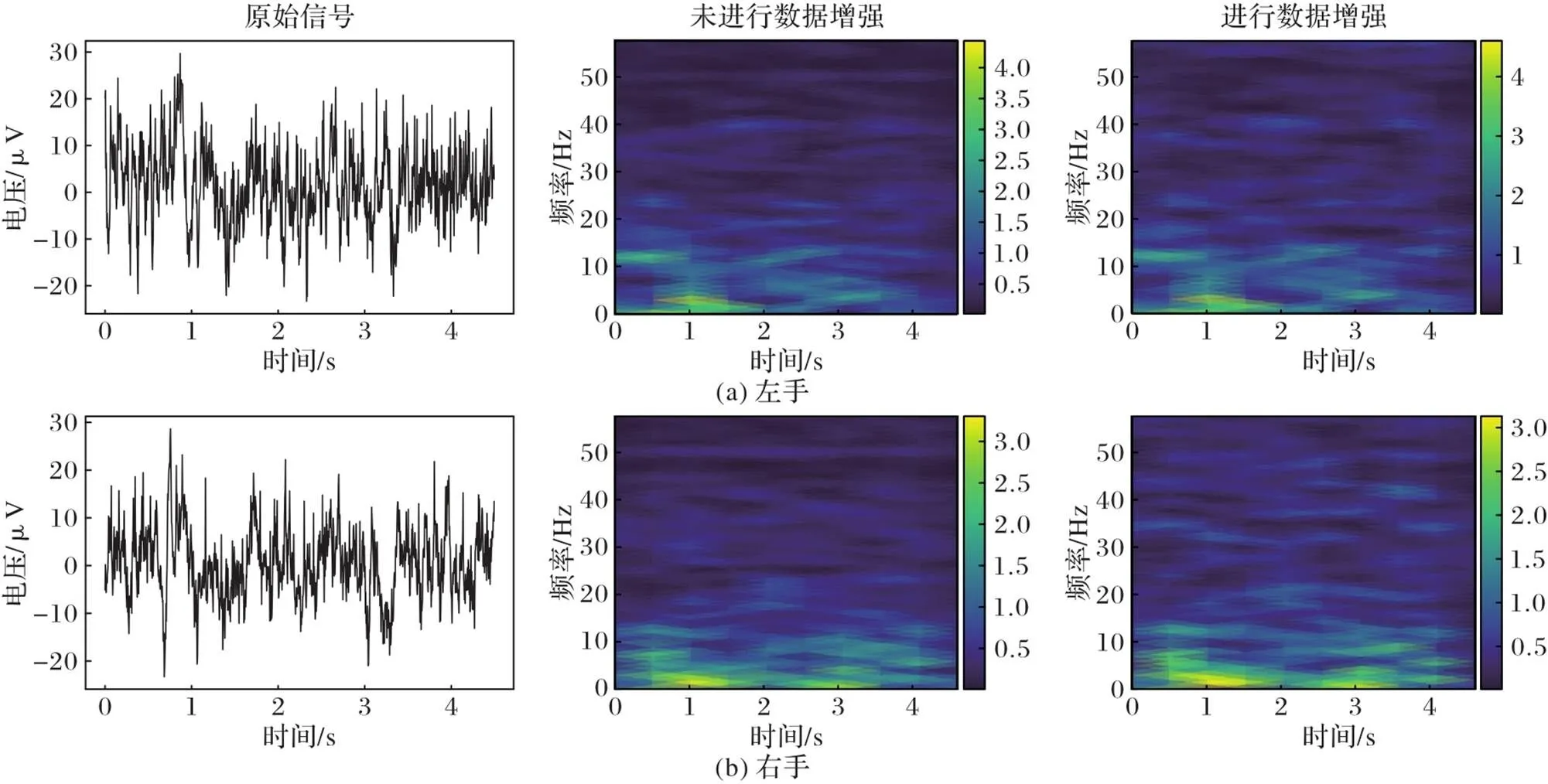
图6 数据增强前后的时频图对比
本文对所有受试者分别使用两种网络模型进行训练和测试,将2a数据集中每个被试的训练子集部分用于训练,测试子集部分用于测试。在训练阶段,每训练完一个epoch就将训练数据的顺序打乱,同时为每个epoch设置了批大小(batchsize)。除了少数受试者的批大小设置为32,其余均为64。两种模型在训练过程中均采用了最小化交叉熵损失函数,同时使用Adam优化器算法对模型参数进行优化,学习率均设置为0.001。本文所有实验代码均使用Python语言编写,其中在网络模型的构建和训练测试部分采用了GPU版的Tensorflow框架。
4 实验与结果分析
4.1 评价指标
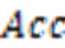
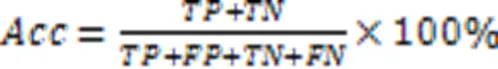
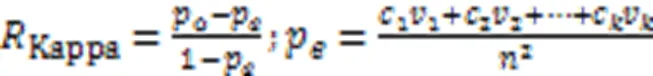
4.2 模型对比
图7展示了4个受试者(A03、A05、A07、A08)在模型训练过程中的准确率曲线。L‑Net由于网络的深度比LH‑Net浅,因此在第100到200个epoch左右便可以很好地拟合训练样本,而在图(a)~(c)中LH‑Net则需要训练400个epoch左右才能拟合数据,训练所需的时间是L‑Net的两倍多。虽然L‑Net能更快地拟合数据,但是从图中可以发现,在训练后期L‑Net的准确率出现了较大波动,而LH‑Net则并未出现这种情况,训练期间的准确率一直比较稳定。
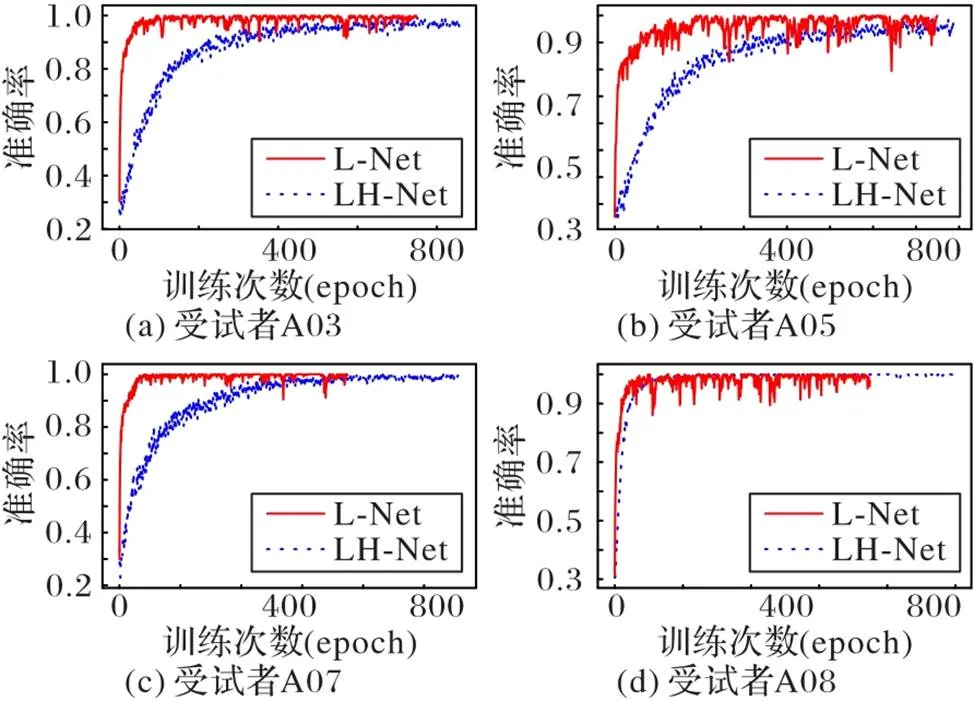
图7 部分受试者的训练准确率
为了验证L‑Net和LH‑Net在运动想象四分类任务上的优势,本文选取了以下几个近几年来在该研究领域中性能表现优秀的深度学习模型进行对比。
1)基于深度可分离卷积构建的EEGNet[9]。它是一种紧凑的卷积神经网络结构,模型的可训练参数仅在2 000左右。该模型在目前最先进的BCI范式上表现出了相当高的性能,且具有很好的泛化能力。
2)基于3D卷积的多分支卷积神经网络(3D Convolutional Neural Network, 3DCNN)[24]。该模型开创性地提出了使用多维阵列来表示EEG信号,并使用3个不同接受视野大小的3D卷积网络来提取运动想象的相关特征。
3)并行的多尺度滤波器组卷积神经网络(Multiscale Filter Bank Convolutional Neural Network, MSFBCNN)[25]。该网络采用多个不同尺度的卷积核来提取EEG的时间特征。
表1展示了本文方法与MSFBCNN、EEGNet、3DCNN在2a数据集上的具体性能表现。从表1中可以发现,深度学习模型在分类性能上远远超过传统的FBCSP,具有更好的泛化能力。其中L‑Net与EEGNet、3DCNN、MSFBCNN的平均准确率和平均Kappa系数相较于L‑Net的总体性能略高于EEGNet同时略低于3DCNN,与MSFBCNN的分类性能则基本保持在同等水平。虽然在受试者A02、A03、A06和A08上的分类表现不佳,但是在A04和A05上的准确率均达到了71%左右,Kappa系数则到达了61%左右,均高于前二者。由L‑Net改进的LH‑Net在平均准确率和平均Kappa系数上分别达到了77.83%和70.44%,相较于EEGNet、3DCNN和MSFBCNN平均准确率分别提高了4.4、1.6和2.9个百分点,平均Kappa系数则分别提升了5.9、2.1和3.9个百分点。同时在A03上将准确率提升到91.57%,Kappa系数则提升到88.76%,均优于EEGNet、3DCNN和MSFBCNN。结合图7的训练情况和表1的测试结果,可以发现LH‑Net虽然在训练时间效率上不如L‑Net,但是在测试集上的表现要更优于L‑Net,性能上具有更好的泛化能力。
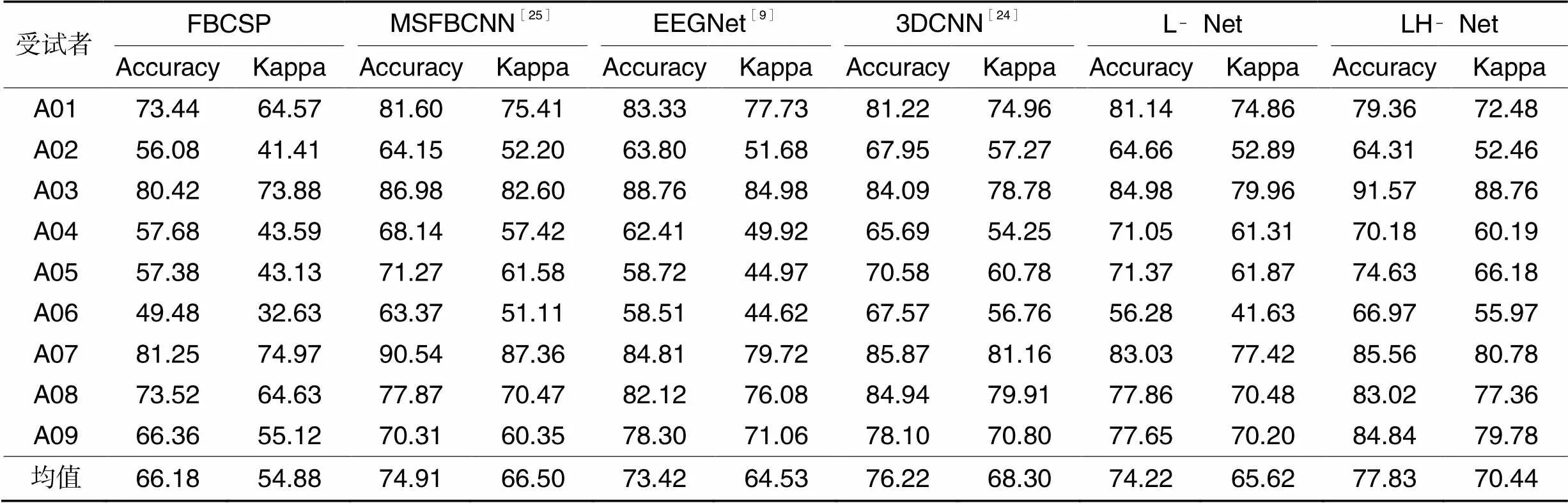
表1 各方法在测试集上的分类性能比较 单位: %
4.3 数据增强分析
本文针对每个受试者均采用了6种不同强度的噪声来生成新的训练样本,并从区间[0.001, 0.5]取值作为噪声的强度值。图8和图9分别为两种模型针对数据集中的9名受试者在采用不同噪声强度的数据增强方法时的分类准确率,图中的横轴坐标代表6种噪声强度的取值,与横轴平行的散点代表不同受试者(A01~A09)未使用数据增强(a01~a09)时的分类准确率。从图8中可以明显发现L‑Net在使用6种不同强度的噪声时,受试者A03、A07、A08的分类精度均比未使用数据增强的分类准确率有了比较明显的提高。其余的几个受试者则只有在特定的噪声强度范围内准确率才有明显提高,其中A02、A04、A06的最优强度范围大致在(0.05,0.001)区间,A05和A09的最优强度范围大致在(0.01,0.5),而A01只有在区间(0.01,0.1)内准确度才有提升。
图9显示,LH‑Net在6种不同强度的噪声下,受试者A01、A02、A04、A05、A06的分类准确率均比未使用数据增强的准确率有了比较明显的提高,与图8相比呈现出一种截然不同的情况。与图8中不同的是,A03、A07、A08、A09的噪声强度最优范围均缩小了,其中:A03的最优强度范围由(0.001, 0.5)缩小到(0.01, 0.5),噪声强度设置过小,分类准确度却降低了;A07和A08的最优强度范围则是由(0.001, 0.5)缩小到(0.001, 0.01),噪声强度过大反而导致了准确率降低;A09在噪声强度过大和过小时均会导致准确率降低,只有在强度为0.01时准确率才会有所上升。
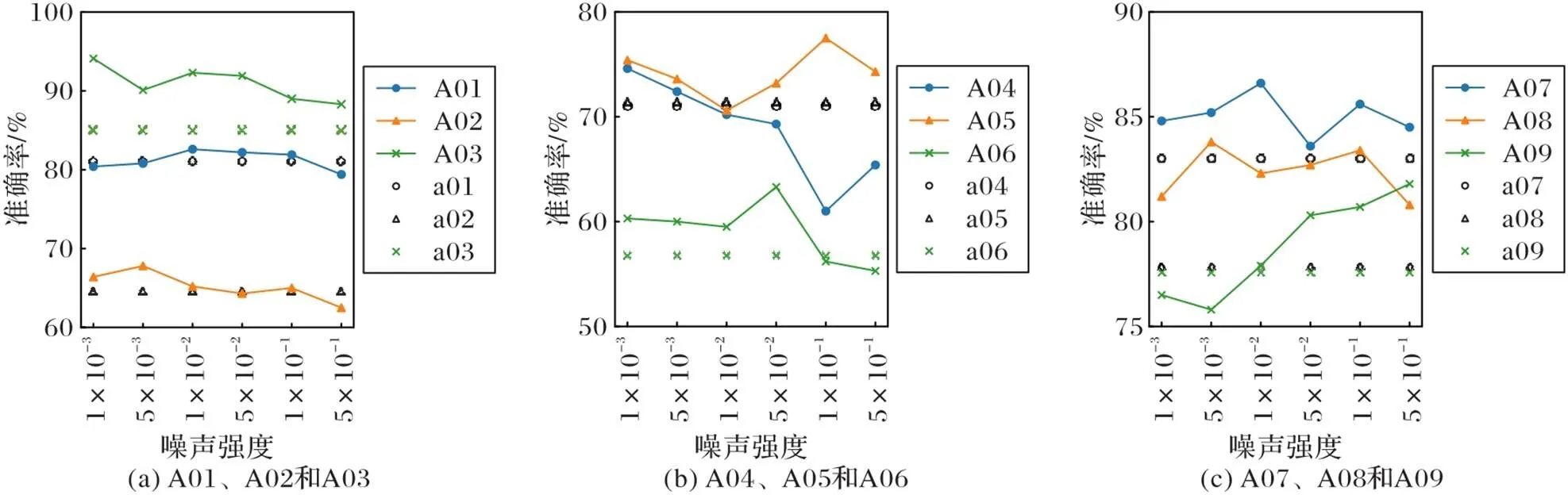
图8 9名受试者在L‑Net上不同噪声强度下的分类准确率
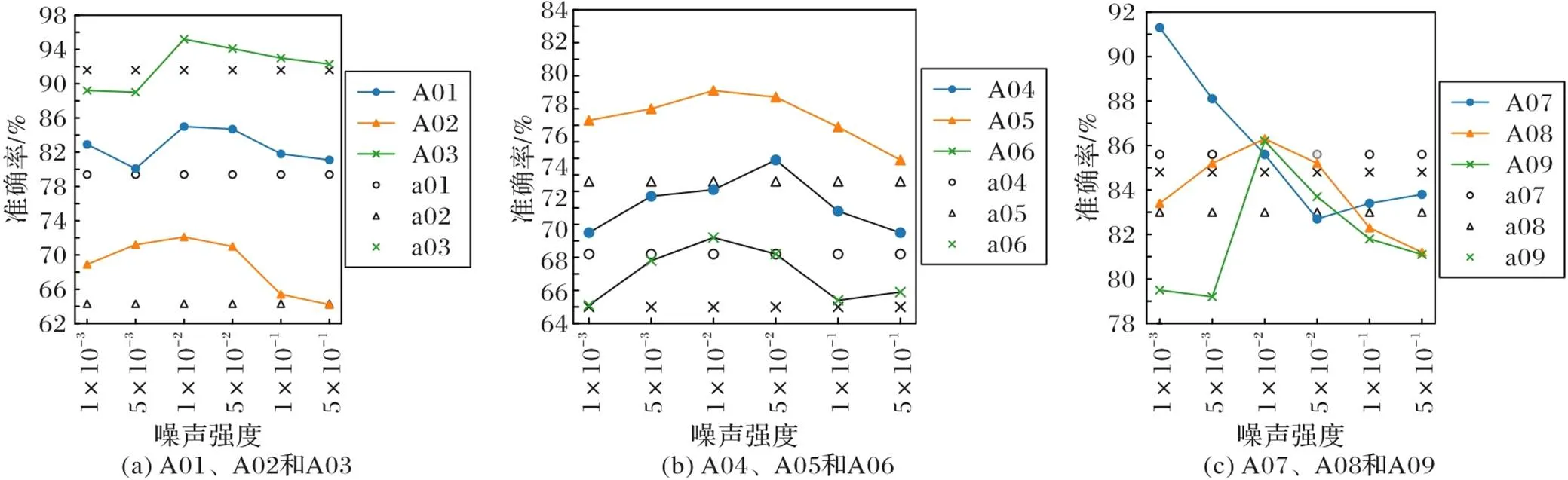
图9 9名受试者在LH‑Net上不同噪声强度下的分类准确率
综上所述,由于两种模型结构之间的差异和不同受试者自身数据的特异性,导致在进行数据增强时噪声的强度成为影响模型性能的关键因素,不同受试者在不同模型上存在不同的最优噪声强度范围。为了探索噪声强度对该数据集总体分类效果的影响,本文在不同噪声强度下,计算得到9名受试者的平均准确率如图10所示。
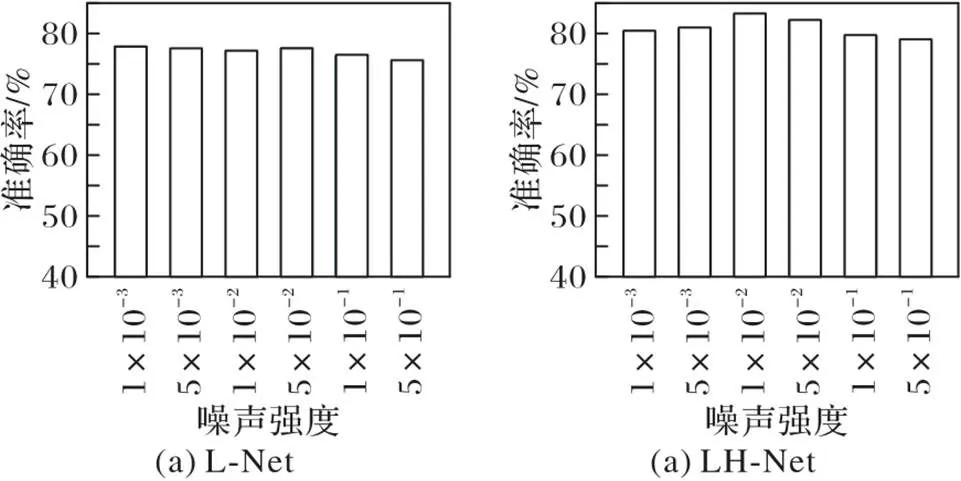
图10 L‑Net和LH‑Net在不同噪声强度下的平均分类准确率
从图10中可以发现随着噪声强度从0.5降低到0.05,两种模型的平均分类准确率都在逐渐升高。其中对于L‑Net模型当噪声强度降低到为0.05时准确度提升到75%左右,之后随着噪声强度的减弱平均分类准确度未有明显的提升。而LH‑Net在噪声强度降低到0.01时,平均准确率上升到最高(81%左右),之后随着强度的减弱平均准确率呈现下降的趋势。由此可初步推断出两种模型的最优噪声强度范围大致分布在(0.001,0.05)、(0.01,0.05)。
表2展示了传统的直接对信号样本进行噪声添加(Noise Addition, NA)与本文基于时频域的噪声添加方法(STFT+NA),两种不同的数据增强方法在L‑Net和LH‑Net两种模型上的分类性能。从表2可以看出,与未进行数据增强之前相比,两种模型的性能指标均得到了有效提升。其中L‑Net和LH‑Net在使用传统的噪声添加方式时,两种分类指标均提升了1~2个百分点;而使用基于时频域的噪声添加方法后,二者的分类指标比使用传统的噪声添加方法提升效果更显著,两者的平均准确率分别达到了79.12%和82.67%。相较于未采用数据增强策略得到的性能指标,L‑Net在平均准确率和平均Kappa系数分别提升了4.90个百分点和6.55个百分点;而LH‑Net则提升了4.84个百分点和6.46个百分点。同时LH‑Net在受试者A03和A07上准确率分别达到了95.24%,91.33%,Kappa系数则达到了93.65%,88.44%。
为了进一步比较两种模型在不同类别上的性能优异,本文在从所有受试者中挑选出最佳噪声强度下的分类模型,并将所有人的预测结果和测试集的真实标签分别合并为一个标签集合来绘制混淆矩阵,同时与未进行数据增强的最优模型进行了对比,如图11所示。其中图11(a)、(c)是在没有使用数据增强的情况下得到的混淆矩阵,图11(b)、(d)是在使用了数据增强的情况下得到的混淆矩阵。从图11可以发现,使用数据增强后,LH‑Net在四个类别上的准确率均有了非常明显的提升,每个类别的精度平均增长了4.8个百分点;而L‑Net虽然在右手这一类别的准确率降低了些许,但其他三类的准确率均有不错的提升,尤其在舌头分类中,准确率由72.6%提升到了83.1%,总体的平均增幅为4.9个百分点。
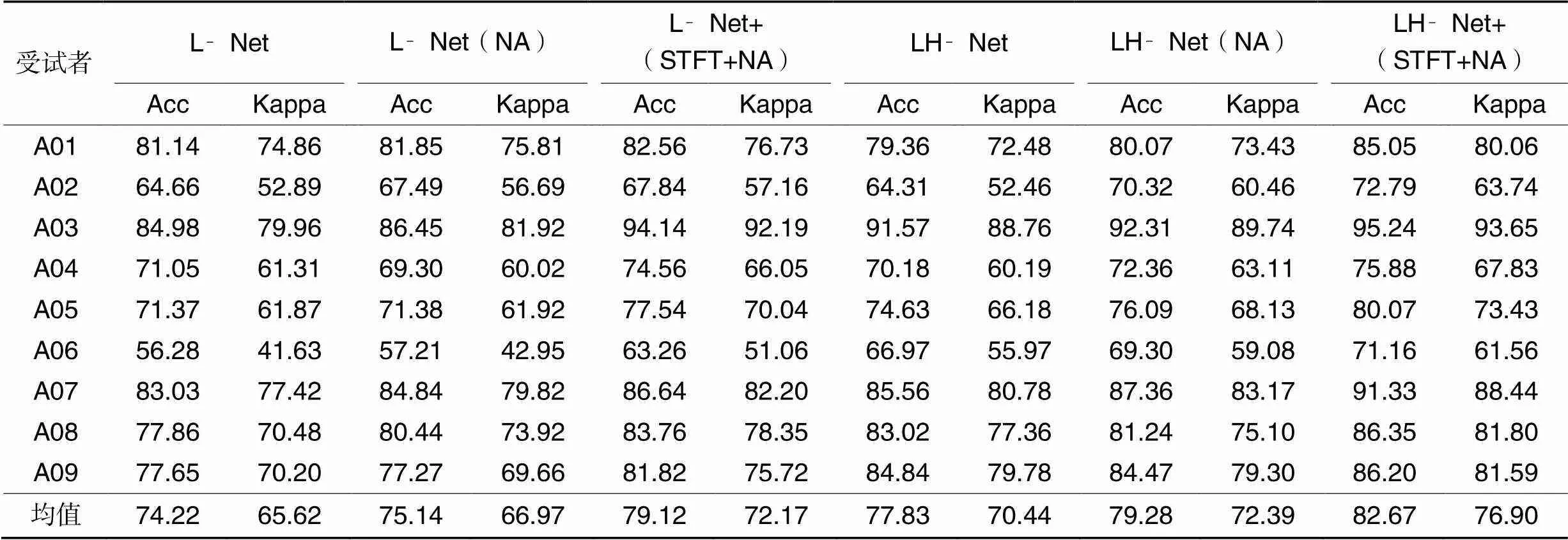
表2 L‑Net和LH‑Net使用不同数据增强方法的分类性能比较 单位: %
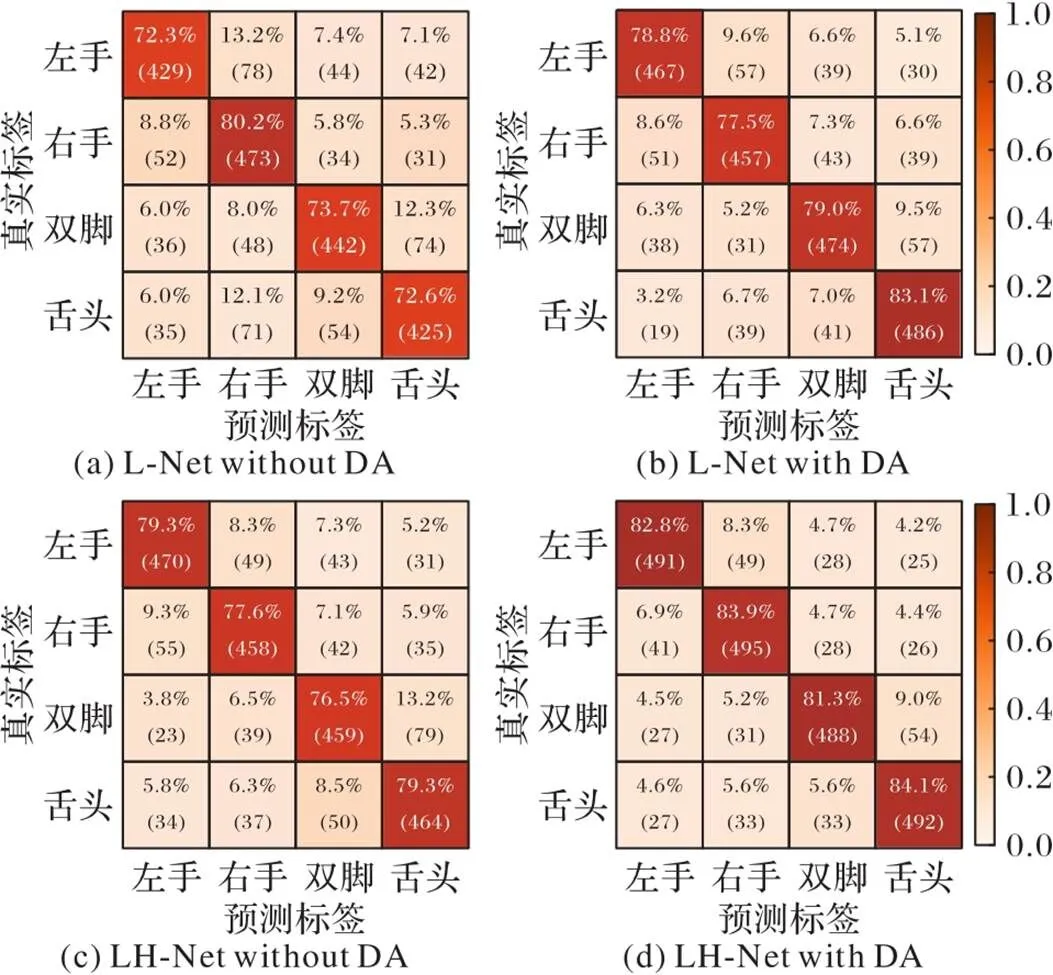
图11 L‑Net和LH‑Net在测试集不同类别上的分类准确率
表3给出了不同模型在相同训练次数时所耗费的时间。从表3可以发现:在未使用数据增强时,LH‑Net总体耗费的时间比L‑Net多161 s,每个受试者的平均训练时间多18 s;在使用数据增强后,由于数据集的样本变为了原来的两倍,二者的总体训练时间和平均训练时间也增加到了原来的两倍左右。结合表2的分类性能分析,虽然LH‑Net与L‑Net相比增加了模型的复杂度,导致训练时间更长,但是模型的分类效果得到了有效提升,同时增加的训练时间在一个可接受的范围。由此可见模型LH‑Net的整体效果要优于L‑Net,同时本文使用的基于时频域的数据增强方法在两种模型上都取得了不错的表现。
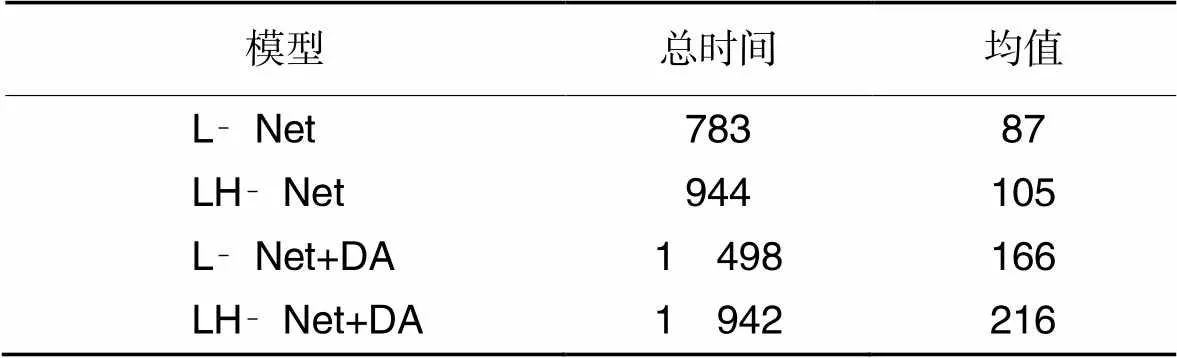
表3 不同模型的训练时间比较 单位: s
5 结语
本文提出了两种不同结构的轻量级网络L‑Net和LH‑Net,它们在运动想象四分类任务中表现良好,且LH‑Net比L‑Net具有更好的鲁棒性,分类性能更好;同时也说明了基于时频域的数据增强方法能够有效提升网络模型的分类效果。本文基于时频域的噪声添加方法与目前使用对抗生成网络的数据增强方法[16]相比,是一种高效、简单的数据增强方法。L‑Net和LH‑Net的优势在于使用了深度可分离卷积,在大幅减少训练参数的同时,能保证模型较好的性能表现;而且由于网络模型规模较小,与3DCNN等大规模的网络模型相比,硬件部署的场景也会更广泛。不过这两个模型在部分受试者上的分类性能表现欠佳,因此我们的下一步工作将从特征选择和迁移学习两个方向继续研究和探索。
[1] LONG J, LI Y, WANG H, et al. A hybrid brain computer interface to control the direction and speed of a simulated or real wheelchair[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2012, 20(5): 720-729.
[2] ANG K K, CHIN Z Y, WANG C, et al. Filter bank common spatial pattern algorithm on BCI competition IV datasets 2a and 2b[J]. Frontiers in Neuroscience, 2012, 6: Article 39.
[3] TONIN L, CARLSON T, LEEB R, et al. Brain‑controlled telepresence robot by motor‑disabled people[C]// Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Piscataway: IEEE, 2011: 4227-4230.
[4] ACHARYA U R, SREEr S V, SWAPNA G, et al. Automated EEG analysis of epilepsy: a review[J]. Knowledge‑Based Systems, 2013, 45: 147-165.
[5] HOSSAIN M S, AMIN S U, ALSULAIMAN M, et al. Applying deep learning for epilepsy seizure detection and brain mapping visualization[J]. ACM Transactions on Multimedia Computing, Communications, and Applications, 2019, 15(1): 1-17.
[6] SAFI M S, SAFI S M M. Early detection of Alzheimer’s disease from EEG signals using Hjorth parameters[J]. Biomedical Signal Processing and Control, 2021, 65: 102338.
[7] ZHANG R, ZONG Q, DOU L, et al. Hybrid deep neural network using transfer learning for EEG motor imagery decoding[J]. Biomedical Signal Processing and Control, 2021, 63: 102144.
[8] CHIARELLI A M, CROCE P, MERLA A, et al. Deep learning for hybrid EEG‑fNIRS brain‑computer interface: application to motor imagery classification[J]. Journal of Neural Engineering, 2018, 15(3): 036028.
[9] LAWHERN V J, SOLON A J, WAYTOWICH N R, et al. EEGNet: a compact convolutional neural network for EEG‑based brain–computer interfaces[J]. Journal of Neural Engineering, 2018, 15(5): 056013.
[10] SAKHAVI S, GUAN C, YAN S. Learning temporal information for brain‑computer interface using convolutional neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(11): 5619-5629.
[11] AMIN S U, ALSULAIMAN M, MUHAMMAD G, et al. Deep learning for EEG motor imagery classification based on multi‑layer CNNs feature fusion[J]. Future Generation Computer Systems, 2019, 101: 542-554.
[12] 杜秀丽,马振倩,邱少明,等.基于卷积注意力机制的运动想象脑电信号识别[J].计算机工程与应用,2021,57(18):181-185.(DU X L, MA Z Q, QIU S M, et al. Motor imagery EEG signal recognition based on the convolutional attention mechanism[J]. Journal of Computer Engineering and Applications, 2021, 57(18): 181-185.)
[13] SCHIRRMEISTER R T, SPRINGENBERG J T, FIEDERER L D J, et al. Deep learning with convolutional neural networks for EEG decoding and visualization[J]. Human Brain Mapping, 2017, 38(11): 5391-5420.
[14] WANG F, ZHONG S‑H, PENG J, et al. Data augmentation for EEG‑based emotion recognition with deep convolutional neural networks[C]// Proceedings of the 2018 International Conference on Multimedia Modeling, LNCS 10705. Cham: Springer, 2018: 82-93.
[15] SCHWABEDAL J T C, SNYDER J C, CAKMAK A, et al. Addressing class imbalance in classification problems of noisy signals by using fourier transform surrogates[EB/OL]. (2019-01-28)[2021-06-19]. https://arxiv.org/pdf/1806.08675.pdf.
[16] ZHANG K, XU G, HAN Z, et al. Data augmentation for motor imagery signal classification based on a hybrid neural network[J]. Sensors, 2020, 20(16): 4485.
[17] HINTON G E, SRIVASTAVA N, KRIZHEVSKY A, et al. Improving neural networks by preventing co‑adaptation of feature detectors[EB/OL]. [2021-09-01]. https://arxiv.org/pdf/1207. 0580.pdf.
[18] CHAUDHARY S, TARAN S, BAJAJ V, et al. Convolutional neural network based approach towards motor imagery tasks EEG signals classification[J]. IEEE Sensors Journal, 2019, 19(12): 4494-4500.
[19] BAI S, KOLTER J Z, KOLTUN V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling[EB/OL]. (2018-04-19)[2021-06-19]. https://arxiv.org/pdf/1803.01271.pdf.
[20] 袁华,陈泽濠.基于时间卷积神经网络的短时交通流预测算法[J].华南理工大学学报(自然科学版),2020,48(11):107-113, 122.(YUAN H, CHEN Z H. Short‑term traffic flow prediction algorithm based on time convolutional neural network[J]. Journal of South China University of Technology (Natural Science Edition), 2020,48(11): 107-113, 122.)
[21] 周飞燕,金林鹏,董军.卷积神经网络研究综述[J].计算机学报,2017,40(6):1229-1251.(ZHOU F Y, JIN L P, DONG J. A survey of convolutional neural networks[J]. Chinese Journal of Computers,2017,40(6): 1229-1251.)
[22] TANGERMANN M, MÜLLER K‑R, AERTSEN A, et al. Review of the BCI Competition Ⅳ[J]. Frontiers in Neuroscience, 2012, 6: Article 00055.
[23] SAMIEE K, KOVACS P, GABBOUJ M. Epileptic seizure classification of EEG time‑series using rational discrete short‑time Fourier transform[J]. IEEE Transactions on Biomedical Engineering, 2014, 62(2): 541-552.
[24] ZHAO X, ZHANG H, ZHU G, et al. A multi‑branch 3D convolutional neural network for EEG‑based motor imagery classification[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2019, 27(10): 2164-2177.
[25] WU H, NIU Y, LI F, et al. A parallel multiscale filter bank convolutional neural networks for motor imagery EEG classification[J]. Frontiers in Neuroscience, 2019, 13: Article 01275.
Motor imagery electroencephalography classification based on data augmentation
PENG Yu, SONG Yaolian*, YANG Jun
(,,650500,)
Aiming at the multi‑classification problem for Motor Imagery ElectroEncephaloGraphy (MI‑EEG), Lightweight convolutional neural Network (L‑Net) and Lightweight Hybrid Network (LH‑Net) based on deep separable convolution were built on the basis of existing research. Experiments and analyses were carried out on the BCI competition IV-2a data set. It was shown that L‑Net could fit the data faster than LH‑Net, and the training time was shorter. However, LH‑Net is more stable than L‑Net and has better robustness in classification performance on the test set, the average accuracy and average Kappa coefficient of LH‑Net were increased by 3.6% and 4.8%, respectively compared with L‑Net. In order to further improve the classification performance of the model, a new method of adding Gaussian noise based on the time‑frequency domain was adopted to apply Data Augmentation (DA) on the training samples, and simulation verification of the noise intensity was carried out, thus the optimal noise intensity ranges of the two models were inferred. With the DA method, the average accuracies of the two models were increased by at least 4% in the simulation results, the four classification effects were significantly improved.
electroencephalography; motor imagery; deep learning; depth separable convolution; data augmentation
PENG Yu, born in 1995, M. S. candidate. His research interests include brain information decoding, deep learning.
SONG Yaolian, born in 1979, Ph. D., associate professor. Her research interests include brain information decoding, communication system.
YANG Jun, born in 1984, Ph. D., lecturer. His research interests include brain information decoding, deep learning.
1001-9081(2022)11-3625-08
10.11772/j.issn.1001-9081.2021091701
2021⁃09⁃30;
2022⁃01⁃05;
2022⁃01⁃28。
TP391.4
A
彭禹(1995—),男,四川泸州人,硕士研究生,CCF会员,主要研究方向:脑信息解码、深度学习;宋耀莲(1979—),女,河南延津人,副教授,博士,主要研究方向:脑信息解码、通信系统;杨俊(1984—),男,云南昆明人,讲师,博士,主要研究方向:脑信息解码、深度学习。

