汽车起重机车架多目标尺寸优化设计

孙丰科，高顺德，徐金帅，奚传峰，郭二棒

汽车起重机车架多目标尺寸优化设计

孙丰科1，高顺德1，徐金帅2，奚传峰1，郭二棒1

（1.大连理工大学 机械工程学院，辽宁 大连 116025；2.大连理工大学 工程力学系，辽宁 大连 116025）

车架作为汽车起重机的重要承载部件，其承载能力对汽车起重机的整车性能有很大影响。本文以55 t汽车起重机车架为研究对象，在SolidWorks中建立参数化模型并导入Workbench中对车架进行有限元分析，计算其极限工况下的应力、变形以及模态。通过参数敏感性分析得到各参数对优化目标的敏感度并确定合理的设计变量。构建以筋板厚度和位置为设计变量的响应面模型，以车架的许用应力为约束条件，基于多目标遗传算法对其进行多目标优化。得到优化结果后对其进行分析确定其合理性。结果表明，优化后的车架满足强度与刚度要求，质量减小了6.3%，第一阶固有频率提高了4.9%。

起重机车架；灵敏度分析；响应面；优化设计

汽车起重机具有操纵灵活、机动性好、能在各种条件下作业的特点，因此汽车起重机发展迅速，被广泛使用在建筑、石化、风电、核电等行业。汽车起重机发展至今，市场竞争日益激烈，在满足结构刚度与强度、整机稳定性等要求的基础上，对其结构进行优化设计，降低制造成本是一种必然趋势。车架重量在汽车起重机各部件的总重量中占据很大的比例[1]。同时，车架作为汽车起重机的主要承载部件之一，其强度和刚度对起重机的安全性、稳定性及可靠性具有重要影响[2]。因此，在保证足够强度和刚度的前提下降低重量对起重机的轻量化以及低能耗发展具有重要意义。于志新等[3]利用Hyperworks软件对某载货汽车车架进行优化设计，对车架的纵梁和横梁厚度进行了优化改进，优化后车架的最大位移由原来的20 mm减至12.3 mm，刚度提高了8%；宋晓飞等[4]基于Optistruct软件对某重型汽车的驱动桥壳进行了轻量化设计，在满足桥壳性能要求的前提下，实现对桥壳减重50.075 kg，减重率达24.78%；苏永红[2]基于PATRAN有限元分析软件对某型汽车起重机截面形状以及板厚进行优化设计，并对改进前后的结构进行对比；张斯亮[5]通过有限元分析，使用ANSYS Workbench对车架截面形式进行设计改进。汽车起重机车架结构较为复杂，内部具有较多的筋板，并且各筋板厚度和位置对结构静动态特性及质量具有不同的影响，可以通过灵敏度分析对设计参数进行筛选。本文通过灵敏度分析得出对车架质量和第一阶固有频率影响较大的参数，并基于多目标遗传算法对其进行优化，进而提高起重机的综合性能。汽车起重机主梁结构的多目标优化设计技术路线如图1所示。

1 模型的建立与仿真

1.1 车架实体模型参数化

车架作为汽车起重机的关键部件之一，整体为焊接框架结构，一般分前段和后段两部分，前段主要用于安装汽车部件，如变速箱、发动机等，后段部分也称之为车架的主体，它采用的是封闭的薄板箱体，主要包括活动支腿、固定支腿箱、回转支撑等部分[6]。在实际工作过程中，车架前段受力远小于后段，故本文主要研究后段部分，结构如图2所示。为使汽车起重机底盘所受载荷均匀，应使回转中心处于合理的位置，支腿布局应保证各工况下起重机稳定性基本相同。

图1 多目标优化设计技术路线图

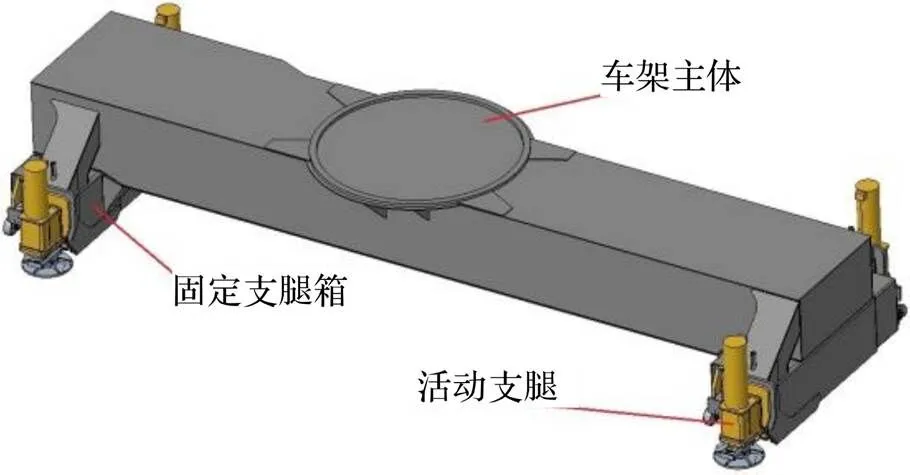
图2 车架结构

因为车架的一些细节对其质量、变形以及应力等影响不大，为了提高计算效率，避免网格形状畸形，在保证分析结果准确性的前提下对车架模型进行简化：忽略为保证焊接余量而预留的板边缘；去除结构中直径小于6 mm的小孔；去除车架拼焊钢板的工艺坡口；同时本文主要研究车架主体的刚度与强度，因此简化模型时省略固定支腿箱以及活动支腿部分。简化后的模型如图3所示，其长宽高为7108 mm、1120 mm、780 mm。

将车架CAD参数化模型中需要分析的设计参数通过Solidworks提供的方程式工具按照有限元软件可以识别的方式进行修改，将设计参数尺寸作为输入参数变量进行分析。汽车起重机车架结构设计参数如图4所示。

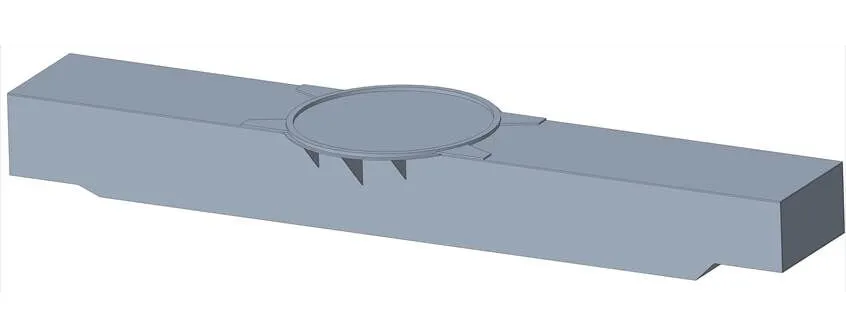
图3 简化车架三维模型

图4 车架设计参数图

1.2 车架有限元分析

将SolidWorks与Workbench进行关联即可通过工具栏将实体模型导入到Workbench中。车架整体使用六面体网格进行划分，加载部位及关键部位进行网格细化，以保证计算结果的准确性。汽车起重机的驾驶室、发动机、悬架等重要部件质量使用mass点代替。有限元网格划分单元数149780，节点数292643，网格平均质量为0.724，可以保证计算结果的准确性。通过Workbench建立的CAE模型如图5所示，图中将侧板隐藏以显示内部筋板。

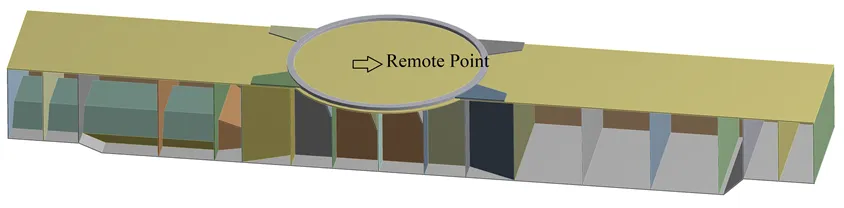
图5 车架有限元模型

车架材料整体选用TQ700MCD高强度钢板，材料的力学性能为：密度7.85×10-9kg/mm，弹性模量2.06×105MPa，泊松比0.3，屈服强度735 MPa，抗拉强度785 MPa，许用应力479.29 MPa。

车架受力主要来自整体的结构自重、吊载质量及工作时产生的力，这些载荷通过回转支承作用于车架。在计算时可将车架受力合成为施加在回转支承中心上的集中力及力矩，在Workbench通过远程点（Remote Points）将载荷施加在有限元模型上。

本文主要分析车架主体自身的刚度、强度及模态，因此可忽略支腿的影响，将约束直接施加在车架固定支腿箱位置。加载工况选择行驶方向左侧45°起吊作业即5 m幅度、12.2 m臂长下起吊43.5 t重物的极限工况，此时车架所受力矩最大。经有限元计算此工况下车架的变形如图6所示、应力如图7所示，可以看出：车架最大位移处位于加载平面所受弯矩方向，最大位移为8.9825 mm，此处结构刚度偏弱，可对结构适当改进；车架最大应力473.74 MPa，是忽略支腿影响及模型简化所造成的应力集中，其他位置的应力约为200～300 MPa，满足材料许用应力要求。

车架模态分析用于确定车架的振动特性，即固有频率和振型[7]。模态分析反映了车架的力学性能，与载荷无关，能全方位地体现车架的结构特性，暴露车架在某方向上的薄弱环节。表1为车架前四阶固有频率，图8为前四阶阵型图，可以看出车架的第一阶固有频率较低，应尽量提高第一阶固有频率，以避免工作状态时产生共振。

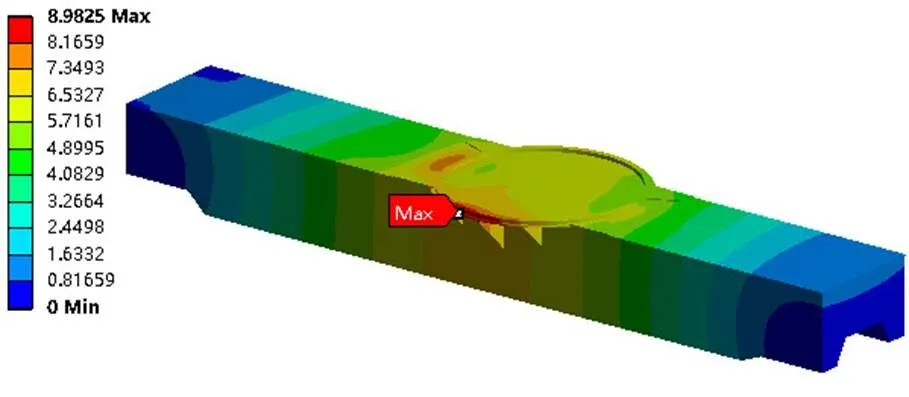
图6 车架变形云图

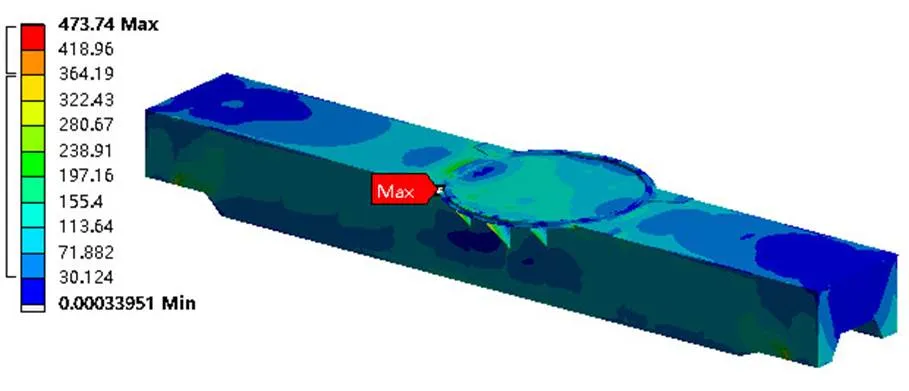
图7 车架应力云图

表1 车架前四阶固有频率

2 多目标尺寸优化

2.1 基于灵敏度分析的响应面优化法

响应面优化设计方法是指使用一定试验设计方法得到数据，利用多元二次回归方法拟合变量与相应值的关系，然后对回归方程进行分析来找到变量的最优值，解决多变量、多目标问题的一种统计方法[8]。响应面优化法在变量取值范围内求解最优值时不需要重复地进行有限元计算，因此相对于直接求解法效率较高。

汽车起重机车架筋板设计参数如图4所示，共选定26个，根据车架结构特点可将部分参数尺寸进行关联：2＝3、4＝5、9＝11、8＝10＝12、14＝15＝H16、18＝19。关联后设计变量为18个，仍然较多，如果对所有的参数进行优化，会导致计算效率大幅降低，同时优化结果的精度也会受到一定的影响。为了高效、精确地对汽车起重机车架进行多目标参数优化，需要对设计尺寸进行灵敏度分析，即通过数学方法计算车架的静动态特性能参数随设计尺寸变化的灵敏度[9]，从而选择出对车架的静动态特性影响较大的设计尺寸。灵敏度分析常用的两种方法为直接求导法与伴随结构法[10]，本文采用直接求导法。

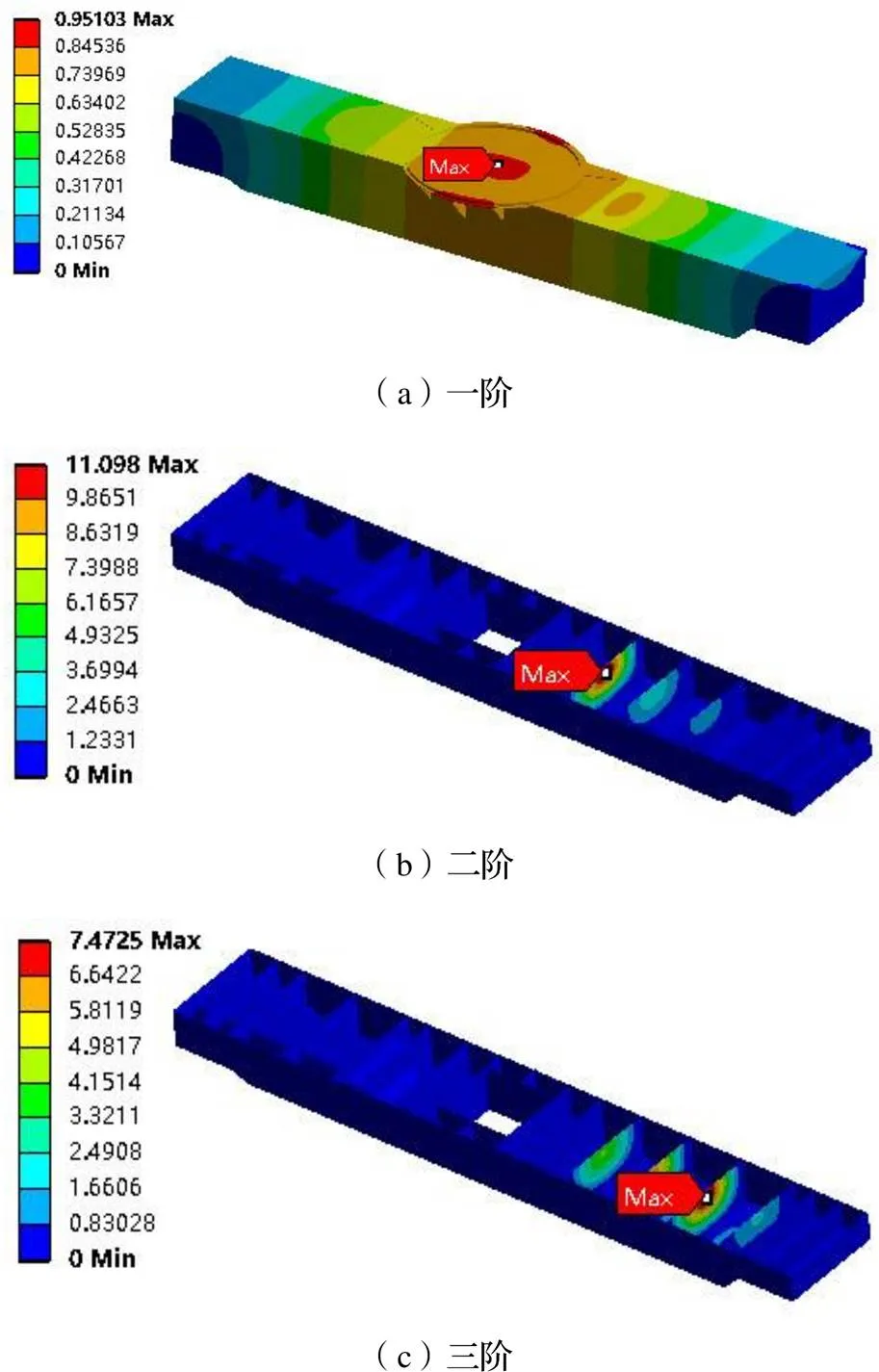
直接求导法的有限元方程为：

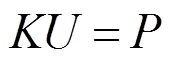
式中：为结构的刚度矩阵；为节点载荷；为节点单元载荷矢量。

式（1）两边对设计变量x求偏导可得：

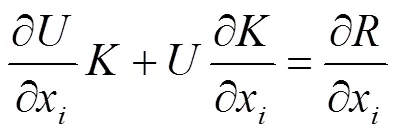
则对的偏导数为：

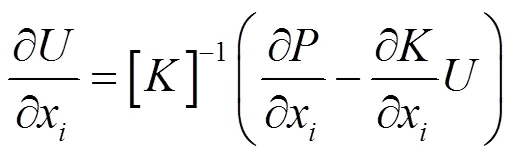
一般来说，优化目标是的函数，即：

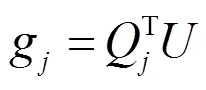
式（4）两边对x求偏导可得优化目标对设计变量的偏导数为：

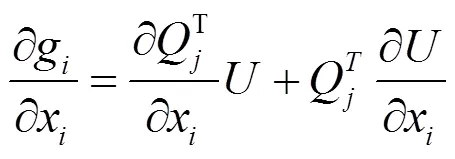
伴随结构法在计算灵敏度时引入伴随变量，满足：

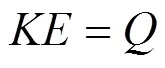
代入式（5）中可得：

其中直接求导法适用于约束条件多而设计变量较少的优化问题，而伴随结构法则相反。

2.2 确定优化变量

本文分析的车架设计参数共有18个，应用Workbench提供的Spearman法对其进行敏感性分析。使用DOE（Design of Experiment，试验设计）技术进行实验样本设计，它是一种对设计方案进行安排和分析实验数据的数理统计方法。为保证准确性，本文设计了100组实验并求解，部分样本设计点如表2所示。

通过响应面模块（Response Surface）得到每个参数分别对第一阶固有频率以及质量的敏感性，如图11所示，结果显示，各设计参数对结构响应的灵敏度各不相同。图9中设计参数的灵敏度为正值表示目标函数的值与该尺寸之间成正相关，设计参数的灵敏度为负值表示目标函数的值与该尺寸之间成正相关。

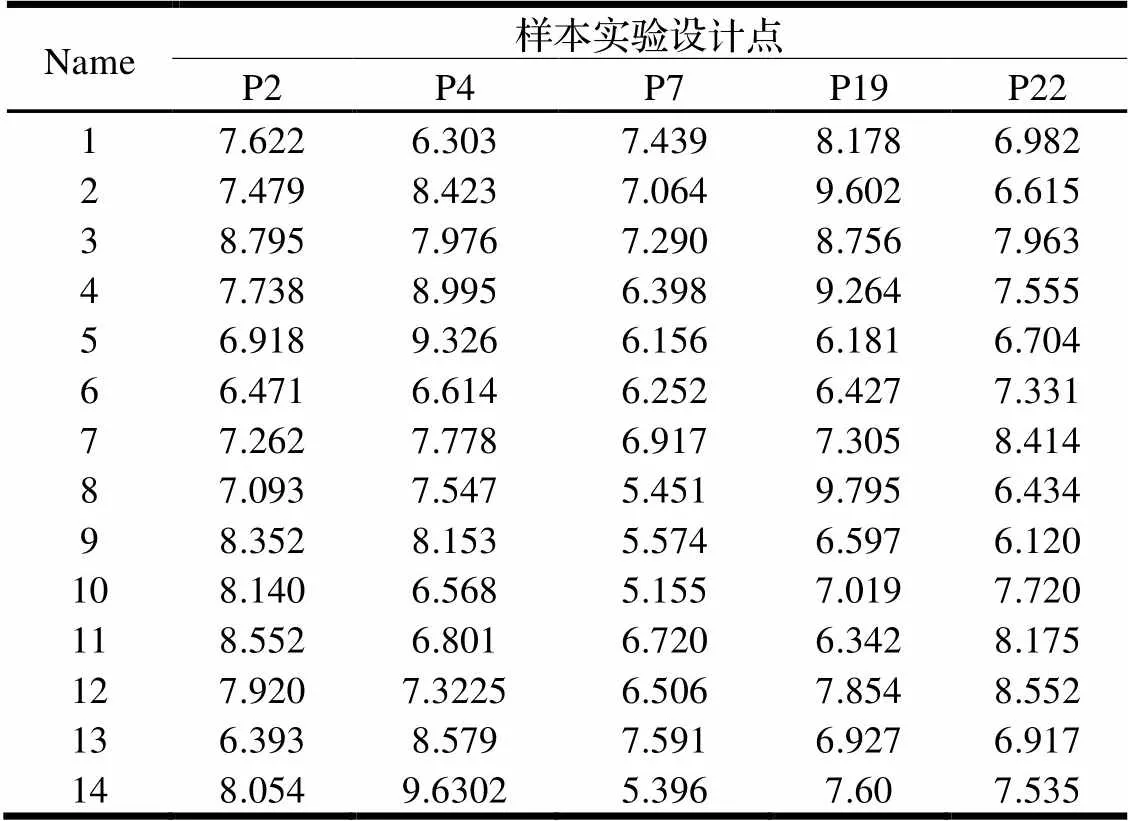
表2 部分样本设计点

图9 设计参数灵敏度分析

通过对图9的分析，综合考虑第一阶固有频率与质量的灵敏度，选择选择2、4、7、9、15、18、1、5这八个尺寸对车架进行最终的尺寸优化，各尺寸的初始值和变化范围如表3所示。

表3 优化尺寸的初始值和变化范围

2.3 基于MOGA的优化求解

汽车起重机车架的多目标优化数学模型可以描述为：

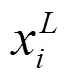
本文采用多目标遗传算法（Multi-Objective Genetic Algorithm，MOGA）对优化模型进行求解，其特点在于适应度的分配机制上，可以通过多个目标函数值来确定单个体的适应度。因此它的收敛速度快并且全局搜索能力强，能够提供一系列的Pareto解[11]，并非是单一解，可以用来处理有约束条件的多目标优化问题。

进入Response Surface Optimization（响应面优化）模块的优化部分，设置MOGA的初始样本数量为100个、每次迭代的样本数为100个、最大迭代次数为20次、最大候选点数为3个。由图10可以观察到算法在运行过程Pareto解百分比的变换情况以及平均值和标准偏差在迭代中的变化情况。

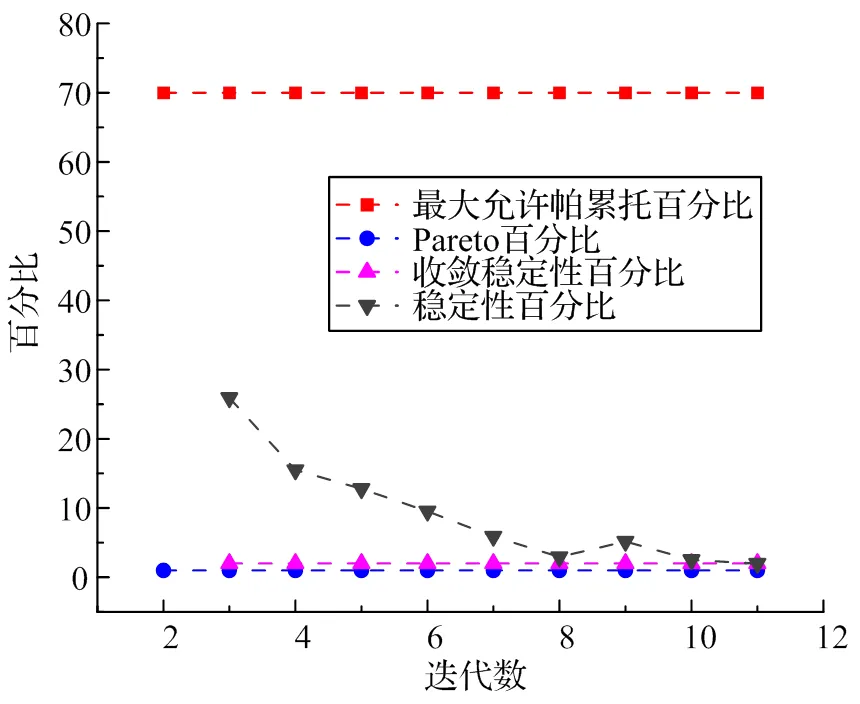
图10 收敛标准图

经求解得到99个Pareto前沿，如图11所示，图中只展现了Pareto点与质量和第一阶固有频率的关系，每一个离散点都代表一个候选点对应的质量及第一阶固有频率之间的值。优化模块会从这些离散点中选取3个候选点，如表4所示。

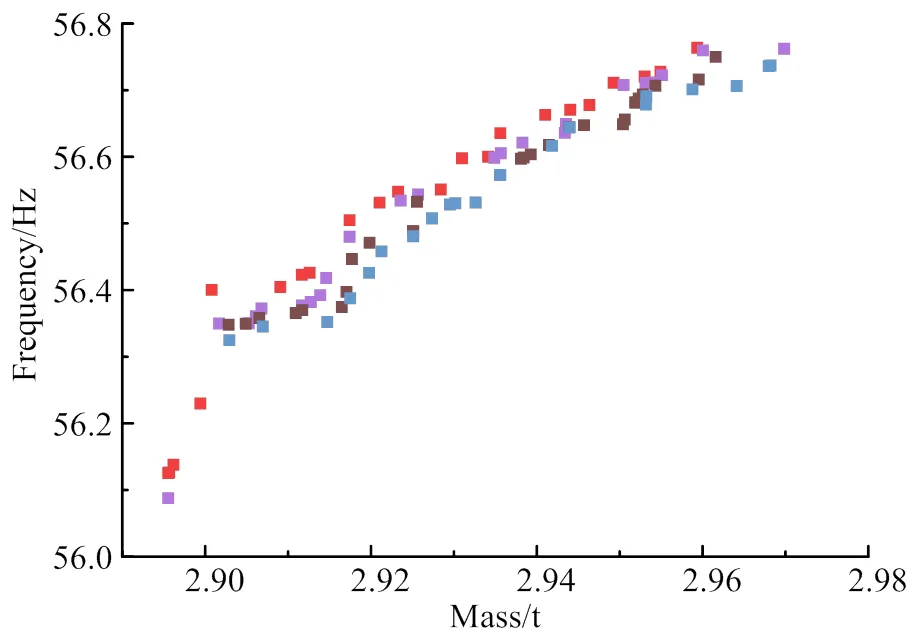
图11 输出参数的Pareto前沿

表4 优化结果候选点

2.4 优化结果分析与对比

通过表4中的数据可知系统提供的三个候选点输出的最大应力值均满足小于许用应力值的约束条件，同时车架的质量相对于优化前有所减小，而第一阶固有频率一定程度增大。本文选择候选点3作为最优解。考虑到实际生产的要求，需要对优化后的尺寸进行圆整，并对汽车起重机结构重新建模并进行有限元分析。优化前后的结果对比如表5所示，可知：最终优化方案建立的车架模型质量减轻了0.196 t，相对于初始模型减轻了6.3%，轻量化效果明显；优化后的第一阶固有频率相对于初始模型提高4.9%，车架的动态特性得到改善；优化后，车架在极限工况下的最大应力为470.79 MPa，满足强度要求，并且应力集中有所减小，车架的应力分布更为均匀；最大变形相对于优化前增大了0.04 mm，可以认为车架的刚度几乎没有发生变化。优化后车架的有限元仿真结果如图12所示。

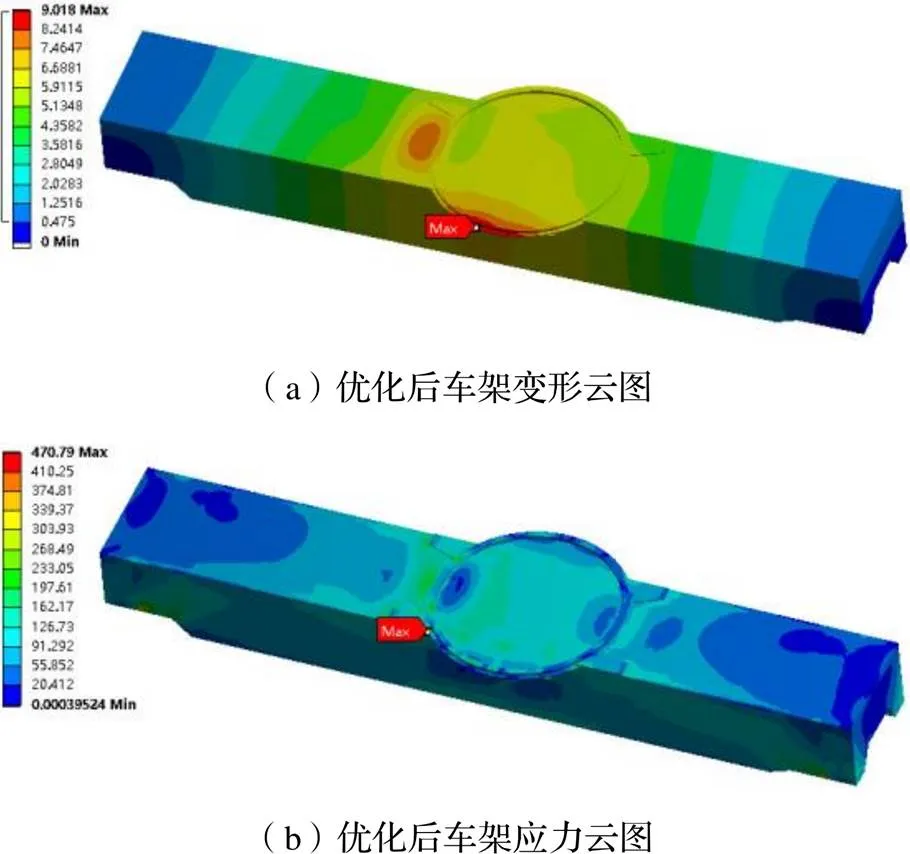
图12 优化后车架仿真结果

3 小结

首先通过对起重机车架结构的分析，提出了多目标尺寸优化的技术路线。通过对车架进行有限元分析，得到车架在极限工况下的静动态特性云图。以车架质量、第一阶固有频率为优化目标，通过对车架的参数尺寸进行灵敏度分析，确定最终的设计变量，然后建立了多目标优化的数学模型。对设计变量的取值范围进行设置，经过实验设计、响应面生成、多目标遗传算法求解得到最终优化方案。

对优化前后有限元结果进行对比表明，优化后的车架在保证刚度与强度要求的基础上，质量减小了6.3%，一阶固有频率提高了4.9%，优化设计效果明显。同时，将多目标优化方法与车架设计过程相结合，可在获得较好产品性能的基础上缩短设计周期，降低制造成本。

[1]刘哲. 汽车起重机结构优化研究[D]. 兰州：兰州理工大学，2016.

[2]苏永红. 汽车起重机车架结构轻量化的分析研究[J]. 机械管理开发，2019，34（12）：43-46.

[3]于志新，曹全德，杨士通. 某载货汽车车架有限元分析及尺寸优化[J]. 机械工程师，2018（1）：18-20.

[4]宋晓飞，林荣会，李帅朝，等. 基于OptiStruct的驱动桥壳轻量化设计[J]. 机械传动，2019，43（4）：83-88.

[5]张斯亮. 16吨汽车起重机车架结构有限元分析及优化研究[D]. 镇江：江苏大学，2018.

[6]姚铁斌. 基于响应面法的堆垛机结构轻量化研究[D]. 湘潭：湘潭大学，2020

[7]杜文学，俞德津. 基于有限元理论的重型半挂车架模态分析[J]. 专用汽车，2007（8）：33-36.

[8]梁其传. 基于自适应稀疏网格模型的桥式起重机主梁结构分析与优化[D]. 武汉：华中科技大学，2019.

[9]周孜亮，王贵飞，丛明. 基于ANSYS Workbench的主轴箱有限元分析及优化设计[J]. 组合机床与自动化加工技术，2012（3）：17-20.

[10]袁宏洲. 装载机结构件动态优化设计[D]. 南京：东南大学，2017.

[11]焦阿允，马新谋，李魁武. 火箭炮底架多目标优化设计[J]. 火炮发射与控制学报，2021（10）：1-6

Multi-Objective Size Optimization Design of Truck Crane Frame

SUN Fengke1，GAO Shunde1，XU Jinshuai2，XI Chuanfeng1，GUO Erbang1

(1.School of Mechanical Engineering, Dalian University of Technology, Dalian 116025, China; 2.Department of Engineering Mechanics, Dalian University of Technology, Dalian 116025, China)

The crane frame, as an important load-bearing component of a truck crane, its performance has a great influence on the performance of the truck crane. This paper takes the 55t truck crane frame as the research object. A parametric model is established in SolidWorks and imported into Workbench for finite element analysis of the frame to calculate the stress, deformation and modal frequency of the frame under extreme conditions. Taking the first-order natural frequency and total mass of the frame as the optimization target, the sensitivity of each parameter to the optimization target is obtained through parameter sensitivity analysis and reasonable design variables are determined. A response surface model with the thickness and position of the tendon plate as the design variables is constructed, and the multi-objective genetic algorithm is adopted to conduct the multi-objective optimization on the model under the constraint of the permissible stresses of the frame. After getting the optimized result, the analysis is conducted to determine its validity. The results show that the optimized frame meets the performance requirements and its weight reduced by 7% and the first-order natural frequency increased by 6%.

crane frame；sensitivity analysis；response surface；optimization design

U63.32

A

10.3969/j.issn.1006-0316.2022.10.011

1006-0316 (2022) 10-0067-07

2021-12-21

孙丰科（1997－），男，山东泰安人，硕士研究生，主要研究方向为结构设计与仿真优化，E-mail：sunfengke1997@163.com；高顺德（1962－），男，辽宁大连人，教授级高级工程师，主要研究方向为工程机械。