基于深度强化学习的飞行器自抗扰控制技术

付京博，邵会兵，詹 韬

(北京控制与电子技术研究所，北京 100038)

1 引言

随着高速飞行器飞行包线的扩大、气动外形的复杂化，使得飞行控制系统模型越来越复杂、不确定性越来越强、非线性特性更加明显、扰动因素更加难以预测。与此同时，新一代高速飞行器对姿态控制系统的敏捷机动能力以及控制精度的要求越来越严格。对于复杂的非线性飞行器控制系统，通常采用的处理方式是：首先对研究对象进行精确的数学建模，然后在系统特征点附近进行小扰动线性化处理，将原来的非线性系统转变成线性系统进行设计。这种方法对数学模型提出了很高的要求，需要建立的数学模型足够精准，才能使后续的设计结果更符合原系统的实际情况。然而，对于复杂的高不确定性、严重非线性、强扰动性被控对象，建立精确的数学模型是一个非常困难的任务。

针对该类问题，韩京清提出了一种不依赖精确模型的控制方法，即自抗扰控制方法，它是一种能够观测系统总扰动并进行实时补偿的控制器，在解决强扰动、高不确定性控制问题方面具有较强优势。自抗扰控制器是以扩张状态观测器为核心的非线性鲁棒控制器，扩张状态观测器不仅可以观测系统的状态变量，同时可以准确的估计出被控对象模型的误差和环境的扰动，而扩张状态观测器的观测品质好坏则直接影响自抗扰控制器的控制品质，因此观测器参数的设计问题是自抗扰控制器设计的关键。文献[1]提出一种依据控制周期h来设计观测器参数——观测误差放大系数——的方法，但由于采用固定参数，适应性较差，应用于高速飞行器这样的参数大范围快变系统时稳定性较差、控制精度不高。

为了解决上述问题，本文提出了基于DDPG的飞行器自抗扰控制技术，应用深度强化学习强大的自学习能力，通过大量的训练，获得不同未知扰动、气动参数大范围摄动等情况下扩张状态观测器的最优参数，避免了因为不可变参数而导致的扰动估计不精准的问题，最后通过仿真验证算法的有效性。

2 控制对象模型与控制算法框架设计

对于高速飞行器，写出其姿态运动微分方程：

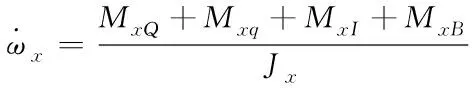
(1)

式中，ωx是角速度，Jx是转动惯量，MxQ、Mxq、MxI、MxB分别是空气动力矩、阻尼力矩、惯性力矩和结构干扰力矩。其中空气动力矩是高速飞行器所受的主要力矩，其余力矩与之相比较小，且具有不确定性，因此将它们当作系统未知扰动的一部分。而对于主要的空气动力矩MQ，将对其进行进一步的分解，分离出已知的部分和未知的部分，根据文献[2]可以得到空气动力矩的表达式如下

(2)

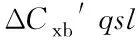
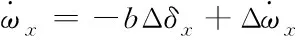
(3)

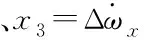
(4)

具有“扰动估计补偿”功能的自抗扰控制器是由以下四个部分组成的：

1) 跟踪微分器是根据系统设定的输入值v安排过渡过程v1，并提取输入的微分信号v2。

2) 扩张状态观测器根据被控对象的输入输出信号估计出被控对象和作用于被控对象的总的扰动。

3) 根据系统的状态误差设计非线性反馈控制律。

将以上安排过渡过程、非线性反馈、扩张状态观测器组合在一起，构成自抗扰控制器，如图1。

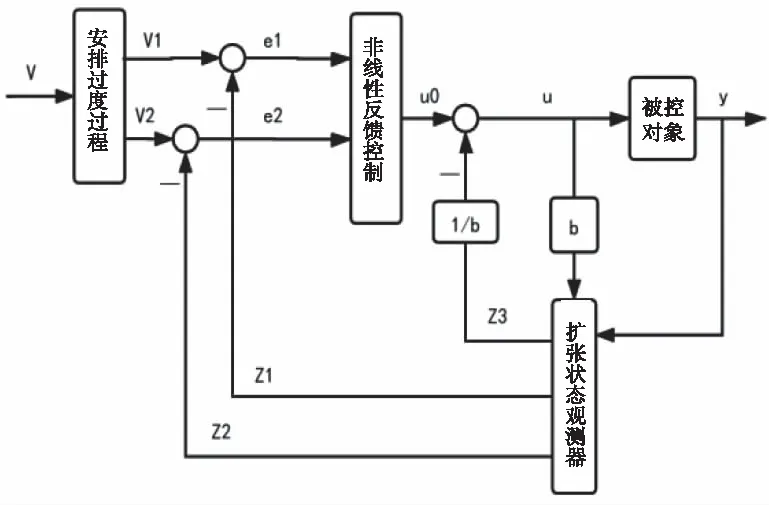
图1 自抗扰控制器原理框图

3 跟踪微分器设计

跟踪微分器用于对姿态角指令安排过渡过程，目的是有限时间单调地跟上输入的姿态角指令信号，无超调的进入稳态，同时也给出此过程的微分信号，作为非线性反馈控制器的输入。在飞行器姿态控制系统设计中，不可避免的需要考虑系统的噪声干扰。对于经典的微分器来说，为了获取更加精确的微分信号，需要更短的采样时间，但会伴随着“噪声放大”的现象。为此文献[1]提出一种最速跟踪微分器，其有很好的噪声抑制能力，离散后的形式如下

fh=fhan(x1(k)-v(k)，x2(k)，r，h).

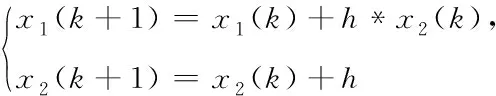
(5)

为了有效的消除微分信号进入稳态后的高频振荡，上式中的函数选择最速控制综合函数记做fh=fhan(x1，x2，r，h)，其算法公式如下

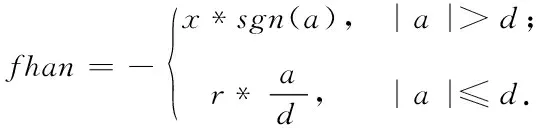
(6)

式中：h为积分步长，r可用于控制跟踪速度的快慢，r越大，跟踪速度越快。

4 非线性反馈控制律设计

本文采用误差和误差微分的适当非线性组合设计反馈控制率，形式如下

u=β0fal(e0，a0，δ0)+β1fal(e1，a1，δ1)

(7)

采用幂次函数fal(e，a，δ)，在a<1时，fal函数具有小误差大增益、大误差小增益的特性，避免了控制器因为误差过大造成控制饱和的现象。引入δ把函数fal改造成原点附近具有线性段的连续函数，避免了高频颤振现象。实际工程中，通常取a1=0.5、a2=0.25、δ=0.01。

5 扩张状态观测器设计

对于自抗扰控制器来说，最核心是扩张状态观测器，通过建立扩张状态观测量的观测方程，使系统具有扰动估计和补偿的能力。

对式(4)状态方程，建立其扩张状态观测器方程

(8)

式中：z1是x1的观测值，z2是x2的观测值、z3为扩张状态变量x3的观测值，也是“总扰动”的观测值。β01、β02、β03是扩张状态观测器的误差反馈增益。通过合理的选择参数β01、β02、β03能够使得“总扰动”的观测值更加接近真实值。

6 基于深度强化学习的自抗扰控制器设计

对被控系统来说，当未知扰动变化范围过大，变化速度过快时，采用固定扩张状态观测器参数的方法控制精度不高，因此结合深度强化学习，设计出了改进的自抗扰控制器。

强化学习是使智能体在与环境的交互过程中，根据不同的观测值采取不同的行为，以最大限度地提高累积奖励的一种算法。如图2。

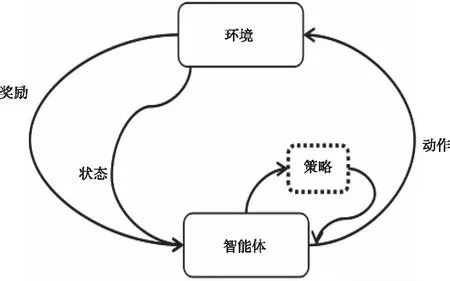
图2 强化学习框图

早期强化学习主要基于表格的方法来求解智能体状态空间和动作空间离散且有限的任务，在实际的环境中，大部分的任务的状态和动作的数量非常庞大，无法用表格的方法进行处理，比如围棋大约有10170种状态等等，这些问题都难以用传统的强化学习算法进行求解。

为了解决上述的问题，学者们提出深度强化学习方法，利用深度学习极强的表征能力，使得智能体能够感知更加复杂的环境状态并且建立更加复杂的行动策略，从而进一步提高强化学习算法的求解与泛化的能力。针对NESO参数在线调节问题，本文采用可以处理连续动作控制的深度确定性策略梯度算法，即DDPG，如图3。

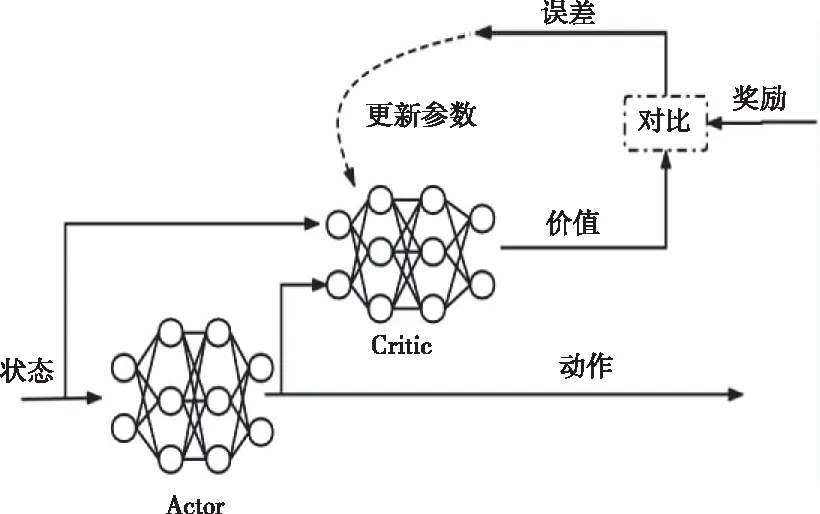
图3 DDPG算法框架

DDPG是基于actor-critic框架的深度强化学习算法，其有两个网络，分别是actor网络、critic网络，其中actor网络负责根据环境反馈的状态，输出系统的连续动作；critic网络是根据系统输出的动作结合反馈的状态，来生成该动作的价值。系统将实际得到的奖励和critic网络输出的奖励进行对比，得到奖励的误差，根据误差，调整critic网络的权值和偏置，使得critic网络的输出估计值更加准确。使用策略梯度算法，沿着提高动作价值的方向更新actor网络的参数。在智能体与环境交互的过程中，两个神经网络的学习参数将得到不断的更新，直到策略收敛。

DDPG算法的目标函数被定义为折扣累积奖励的期望，即

Jβ(μ)=Eμ[r1+γr1+γ2r2+γ3r3+…+γnrn]

(9)

为了找到最优确定性行为策略μ*，等价于最大化上式目标函数Jβ(μ)，即

μ*=argmaxJ(μ)

(10)

根据文献[3]可知，目标函数Jβ(μ)关于策略网络参数θμ的梯度，等价于动作值函数Q(s，a；θQ)关于θμ的期望梯度，因此根据链式求导法则，对目标函数进行求导，得到actor网络的更新方式

∇θ μJ≈Est～ρβ[∇θ μQμ(st，μ(st))]

=Est～ρβ[∇θ μQμ(s，a；θQ)|s=st，a=μ(st；θμ)]

(11)

式中Qμ(s，μ(s))表示在状态s下，按照确定性策略μ选择动作时，能够产生的动作状态值Q；Es～ρβ表示状态s符合分布ρβ的情况下Q值的期望。

又因为确定性策略可以表示为a=μ(s，θμ)的形式，上式可以写成

(12)

对上式使用梯度策略算法，沿着提高动作值Q(s，a，θQ)的方向更新策略网络的参数θμ。

价值网络的损失函数：

L(θQ)=E[(TargetQ-Q(s，a，θQ))2]

(13)

基于式(14)计算神经网络模型参数θQ的梯度

∇θQL(θQ)=E(TargetQ-Q(s，a，θQ)) ∇θQQ(s，a，θQ)(14)

上式中目标函数表示为：

TargetQ=r+γQ′(s′，μ(s′；θμ′))

(15)

式中Q′ 为目标Q值，θQ′和θμ′分别表示目标策略网络和目标价值网络的神经网络参数。价值网络参数的更新和策略网络参数的更新交替迭代，只使用单一的神经网络进行强化学习时，动作值的学习过程很容易出现不稳定现象，所以DDPG算法为价值网络和策略网络各设计两个神经网络，分别是：在线网络和目标网络。

训练价值网络的过程，就是寻找价值网络中参数θQ的最优解的过程，DDPG算法训练的目标是最大化目标函数Jβ(μ)，同时最小化价值网络Q的损失函数。DDPG伪代码如下。

DDPG算法伪代码

初始化：

1) 随机初始化actor网络Q(s，a；θQ)和actor网络μ(s；θμ)的权重参数θQ、θμ

2) 初始化目标网络Q′ 和μ′ ，其中网络的权重参数为θQ→θQ′、θμ→θμ′

3) 初始化经验回放池R

在M个回合内：

随机初始化过程N以进行动作探索

获得初始状态值s0

在次数T内：

1) 根据当前带有噪声的策略计算当前时间步的动作at=μ(st；θμ)+Nt。

2) 执行动作at，并获得奖励值rt和新的状态st+1。

3) 将当前状态st，当前动作值at，当前奖励值rt和下一个状态st+1存储在经验池R中

4) 从经验池R中随机采样小批量的N个转换经验样本(si，ai，ri，si+1)。设

yi=ri+γQ′(si+1，μ′(si+1；θμ′)；θQ′)。

5) 最小化损失函数更新critic网络。

6) 使用梯度策略算法更新actor网络。

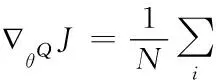
∇θQμ(st；θμ)|sist

7) 更新目标网络。

θQ′←τθQ+(1-τ)θQ′

θμ′←τθμ+(1-τ)θQμ′

结束循环

结束循环

针对飞行器姿态控制系统的扩张状态观测器方程(9)，通过对方程进行拉普拉斯变化和消元整理，可以求出状态观测器输出Z3和被控对象输出y之间的传递函数

(16)

特征方程为

s3+β01s2+β02s+β03

(17)

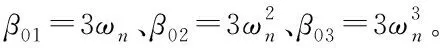
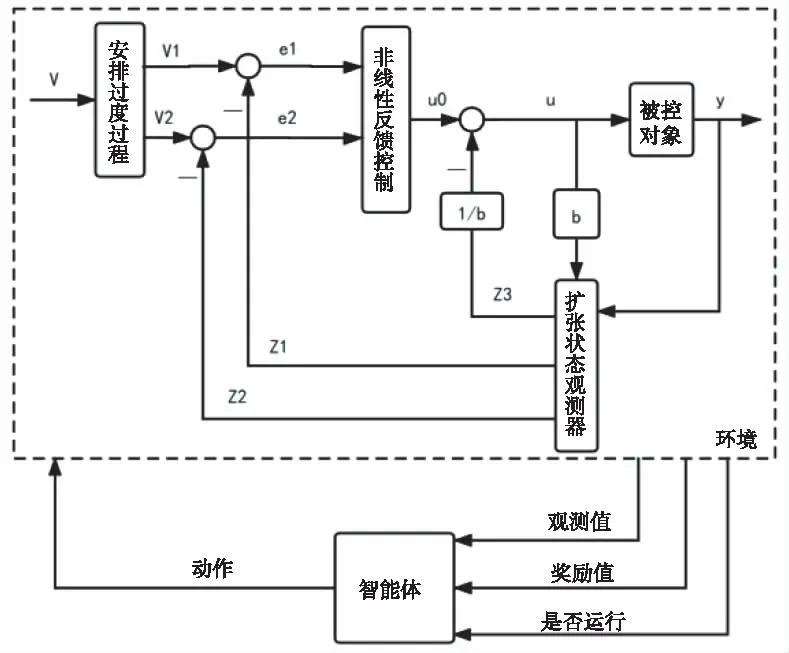
图4 基于深度强化学习的自抗扰控制器结构框图

根据图(4)设计的控制系统结构框图设置深度强化学习智能体的各项参数：

状态空间：输入的指令姿态角v、跟踪微分器跟踪的指令姿态角的值x1与状态观测器观测值z1的差(记做e1)、跟踪微分器跟踪的指令姿态角的微分的值x2与状态观测器观测值z2的差(记做e2)、跟踪微分器跟踪的指令姿态角的值x1与控制对象的输出y的差(记做ey)、

动作空间：扩张状态观测器的极点

奖励函数：设置奖励函数R=-(20|e1|+5|e2|+40|ey|)-100d+g(ey).式子中g(ey)是相邻两个时刻的ey的积分差的函数，d为设置的截至因子，一般d=0，但当系统误差ey过大时，返回值d=1。

智能体中的由状态空间到动作空间的映射函数、状态空间和动作空间到动作值得映射函数用神经网络代替。

在simulink中搭建控制系统仿真模型，采用离线训练的方法，给定系统期望姿态角输入，系统中人为的增加方波干扰，设计深度强化学习与自抗扰控制相结合的控制器，使得输出可以跟踪期望姿态角，提高控制系统精度，增强系统鲁棒性。

7 仿真研究

针对深度强化学习自抗扰控制器，采用正弦信号作为系统的输入，同时为了模拟强干扰的环境，在仿真中增加了大小为[-1，1]的单位方波信号作为干扰信号，设置强化学习模块的仿真次数450次，仿真步长为0.01s，智能体每一回合时间为5s。通过对智能体450回合的训练，可以得到一个在有模型误差，强未知扰动等干扰的情况下，仍能自动调节扩张状态观测器极点ωn，得到精确的“总扰动”的观测值，进而控制系统可以精准的跟踪输入信号，得到更好的控制效果的控制器。训练完成之后，通过改变干扰信号的大小和被控对象气动参数测试智能体的训练与泛化的效果。

测试基于深度强化学习自抗扰控制器与固定参数的传统的自抗扰控制器对高不确定性、严重非线性、强扰动性的系统的控制效果，采取以下3种方法：

1) 将状态方程中的模型参数b增大50%。

2) 将状态方程中的模型参数b缩小50%

3) 仅将干扰信号增大5倍，频率增加1倍。

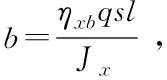
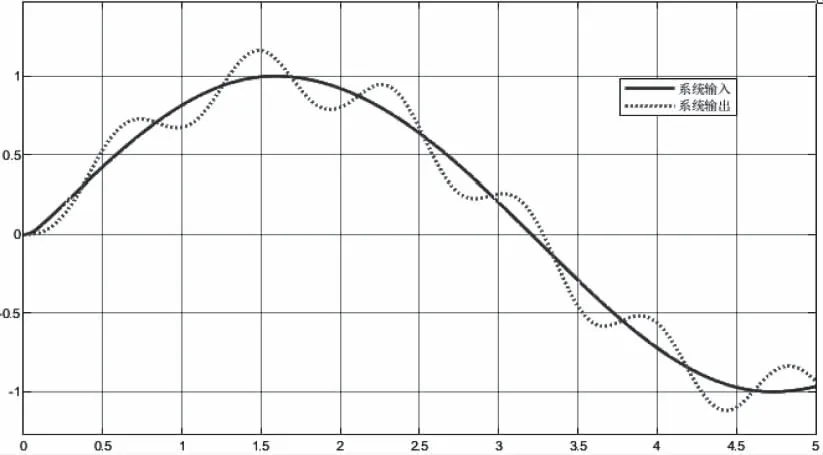
图5 传统自抗扰控制器控制效果图

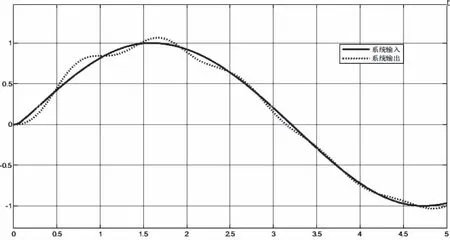
图6 改进的自抗扰控制器控制效果图

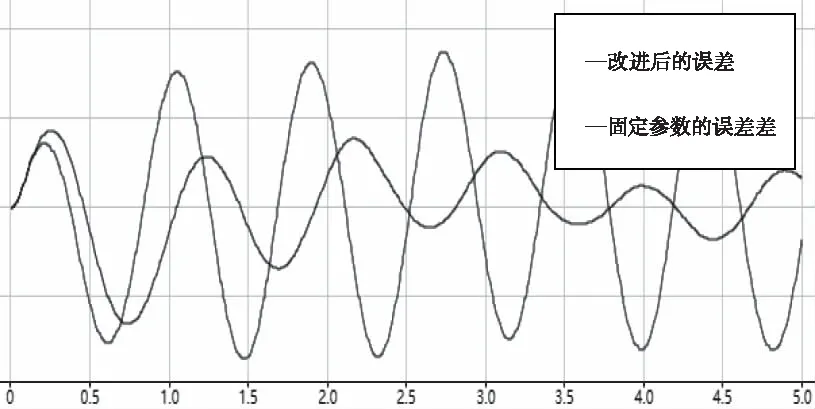
图7 误差大小对比

当模型参数b缩小50%时，对比传统控制器与改进的控制器的控制效果，如图8、图9和图10。

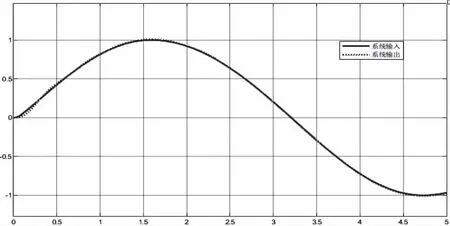
图8 传统自抗扰控制器控制效果图

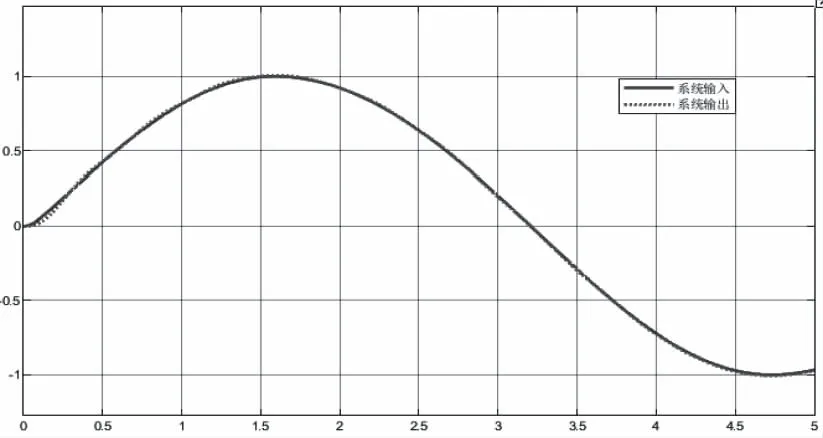
图9 改进的自抗扰控制器控制效果图

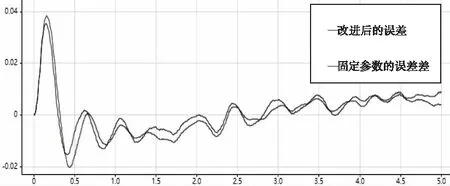
图10 误差大小对比

当干扰信号增大5倍，频率增大1倍，如图11。对比传统控制器与改进的控制器的控制效果。如图12、图13和图14。

图11 扰动方波信号

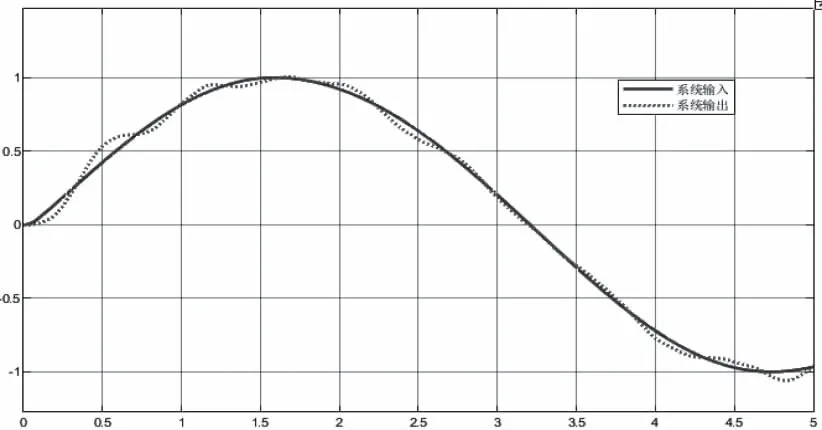
图12 传统自抗扰控制器控制效果图

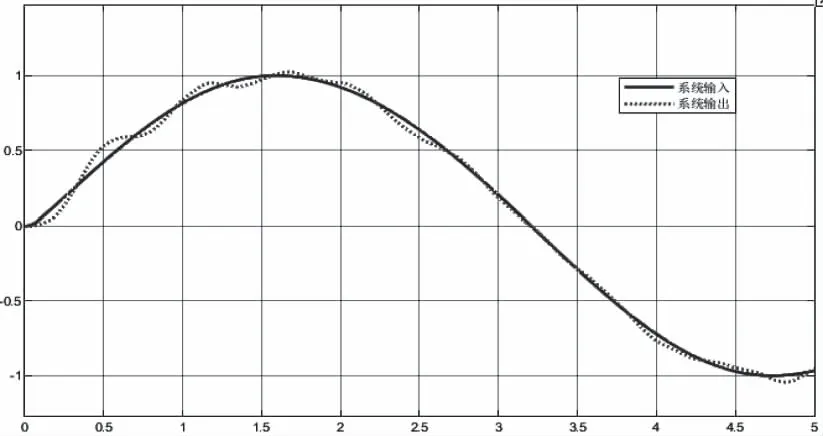
图13 改进的自抗扰控制器控制效果图

图14 误差大小对比

通过对以上仿真结果的分析可以得出，当系统的气动参数摄动到-50%时，两种方法的跟踪效果均很好，改进的自抗扰控制器的跟踪误差略小于传统的自抗扰控制，结果如图10所示。当人为增大干扰信号的大小和频率时，两种方法的跟踪效果均很好，改进的自抗扰控制器在仿真时间大于3.5s之后，跟踪误差小于传统的自抗扰控制，结果如图14所示。

当系统的气动参数摄动到+50%时，两种方法的跟踪效果有明显的差别，如图7所示，传统的自抗扰控制器的跟踪误差在[-0.4，0.4]之间浮动，基于深度强化学习的自抗扰控制器由于其强大的自学习能力，可以根据气动参数的变化，自动的调整到扩张状态观测器的最优参数，使得跟踪误差在[-0.2，0.2]之间浮动，且越来越小。对比传统的自抗扰控制器，跟踪误差有明显的减小，控制效果更好。

8 结论

本文针对高超声速飞行器飞行过程中存在快变的扰动，大范围的气动参数摄动，且飞行需要精确控制的要求，提出了一种深度强化学习的自抗扰控制技术，通过深度强化学习算法离线训练智能体，使智能体在与复杂环境的交互中，获得扩张状态观测器的最优参数。对比传统的固定参数的自抗扰控制器，大大节省了繁琐的人工调参时间，对未知快变扰动的估计更加精准，极大的增加了算法的可适应性。仿真结果表明：基于深度强化学习的自抗扰控制技术对高不确定性、严重非线性、强扰动性的高超声速飞行器的控制精度更高，鲁棒性更好。