扭旋角度对新型静态混合器混合性能的影响
李星宇,张春梅,杨鹏达
(沈阳化工大学 机械与动力工程学院,辽宁 沈阳 110142)
SK型静态混合器是一种传统的静态混合器,可适用于石油化工、精细化工、生物石油加工等领域的搅拌、反应、提纯、传热等流程。国内外学者对SK型静态混合器的混合特性开展了广泛的研究,得到了许多重要的结论。孟辉波等[1-2]进行了 SK型静态混合器的湍流流动数值模拟,揭示了 SK型静态混合器切割区内部流动阻力特性和混沌运动特性,为了提高 SK型静态混合器的性能,一些学者对其结构进行了改进,设计了新型静态混合器;Hobbs等[3]在低雷诺数条件下,对Kenics 型静态混合器进行了模拟研究,得出改变扭旋元件的长径比时,能够影响静态混合器的混合效率;龚斌等[4]对多叶片的静态混合器内的流场进行了分析,发现静态混合器内有强弱漩涡,强化径向混合;王宗勇等[5]对多流道螺旋静态混合器的混合性能进行了研究,得出流道的增加能够增强流体混合效率、缩短混合元件长度。本文在 SK型静态混合器结构的基础上,结合多流道的思想,提出一种新型的静态混合器,利用Fluent进行数值模拟仿真,改变扭旋角度时,对该静态混合器混合性能的影响进行研究。
1 研究对象及方法
1.1 新型混合器的几何结构
本文研究的静态混合器由一根主管、一根支管、四个混合元件组成,如图1所示。
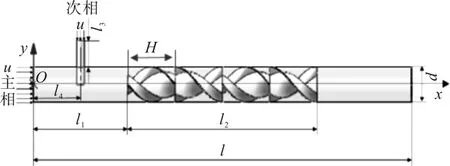
图1 静态混合器结构示意图
在混合管内SK形混合元件和扭旋片同心布置,中心1/2直径处为SK型混合元件,外围1/4直径为关于原点呈中心对称的夹角β=90°的扭旋片组成,扭旋片长度为H,扭旋角为α,相邻两个混合元件中左旋螺旋板和右旋螺旋板在管内呈错开90°交替排布,如图2所示,静态混合器的主要几何结构参数如表1。

图2 静态混合器元件的几何模型(α=180°)
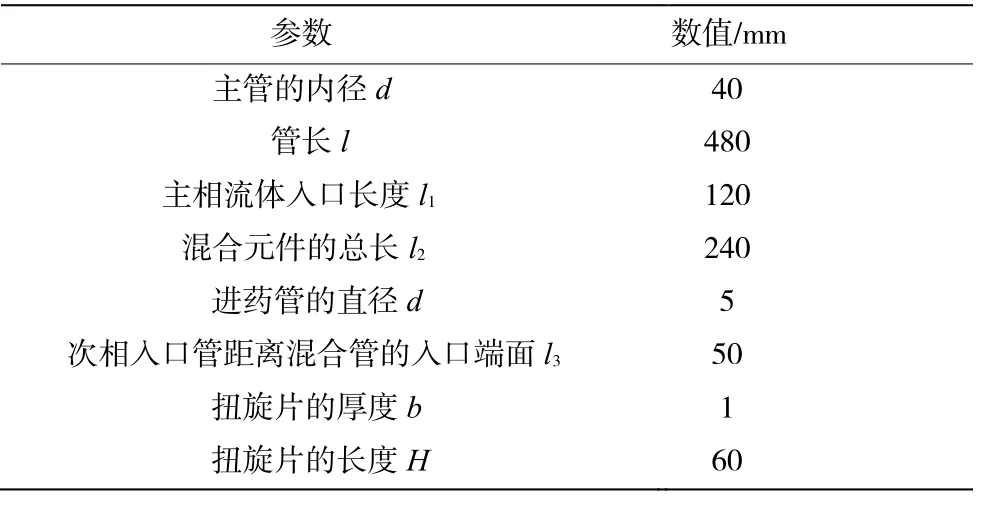
表1 静态混合器的几何尺寸
1.2 模拟方案
模型使用Solidworks进行建模,使用Fluent对静态混合器内的流体浓度场进行数值模拟。模拟研究的主相采用20 ℃水(密度为998.2 kg·m-3,黏度为0.001 003 Pa·s),次相为H2SO4(密度为1 836 kg·m-3,黏度为0.010 18 Pa·s);两种流体均为连续的不可压缩的牛顿流体,忽略重力的影响。多流模型采用mixture[7]模型。设定主相流动方向为X轴正方向,建立如图1的坐标系。 假设所有物性参数都是定值,主相与次相的入口速度相同,采用均匀速度的入口边界,出口边界条件选用自由出流。压力与速度耦合选择SIMPLC算法。
静态混合器内的流体流动状态利用主相入口的雷诺数Re为参照,由雷诺数计算公式(1)可得主相的入口速度。

式中:ρ—流体密度,kg·m-3;
u—入口流体速度,m·s-1;
d—入口内径,mm;
μ—流体动力黏度,Pa·s。
1.3 网格无关性检验
在对研究对象进行网格划分时,如果网格划分数量过大,造成计算量太大,收敛速率低,而网格划分数量过少时,可能达不到所需计算精度,为此,根据流体流过最后一个混合元件的分离强度I确定合适的网格数量。
分离强度为流体的实际浓度方差与尚未混合时的方差的比值,表达式如(2)。

式中:X—对某一截面内H2SO4的m个采样点的体积分数平均值;
Xi—某一截面中不同位置H2SO4的体积分数。
在主相的入口雷诺数Re=1 200的情况下,对α=150°静态混合器内浓度场模拟计算, 所得流体流过最后一个混合元件的分离强度随网格密度变动情况如图3所示。在图中, 可发现网格总量在2 188 474以后的变化起伏明显降低, 变化不超过5%, 亦即当网格总数超过2 188 474之后,分离强度就基本不再改变, 而此时的网格总量也不再影响运算准确度,故本文选择网格数在2 188 474以上进行模拟计算。

图3 分离强度随网格数量变化曲线
2 混合性能
在主相的入口雷若数Re=1 200的情况下,对α=90°、120°、150°、180°四种混合器内浓度场进行数值模拟。
2.1 轴向浓度分布
不同扭旋角对应的静态混合器轴向截面 H2SO4浓度分布云图,如图4所示。
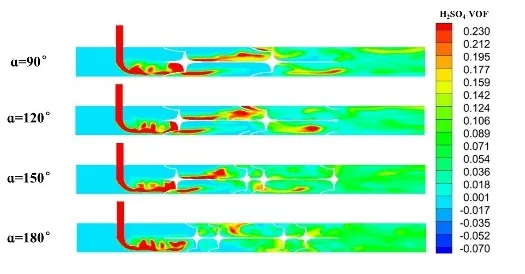
图4 混合器轴向截面的H2SO4体积分数分布云图
由图4可以看到两种流体在第一段混合元件混合前两种流体几乎尚未混合,经过第一个混合元件后,混合区域开始逐渐扩大。流体经过4个混合元件扭旋作用基本都能达到均匀混合的效果。混合元件能够加速混合过程,使流体加速扩散过程。当扭旋角从90°增大到180°,可以明显看到混合元件的混合能力随着扭旋角的增大而增强,扭旋角为180°时,能够在最少的混合元件的条件下达到相同的混合效果。
2.2 径向浓度分布
不同扭转角度在每个扭转元件的首尾径向H2SO4的的体积分数分布云图如图5所示。
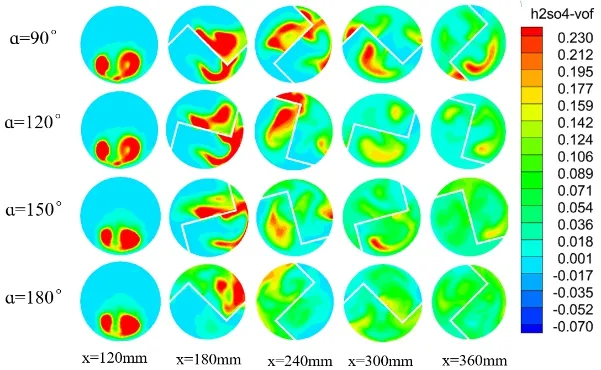
图5 径向H2SO4体积分数分布云图
从图5可以看到,x=120 mm截面次相即使通过加药管汇入主流管道中,在混合元件前的管内几乎没有发生混合。在经过第一个混合元件后,可以观察到x=180 mm截面的两流体开始出种现交错,说明两种流体开始在混合元件的扭旋作用下被分割成多个区域。x=240 mm截面的次相混合更加均匀,混合的效果明显改善,此时将混合效果进行比较可以发现,α=90°和α=120°下仍存在高浓度区域,故混合效果相对较差。在流体到达的x=300 mm时,α=180°的混合元件使得流体基本混合均匀,α=90°仍存在部分高浓度区域,α=120°和α=150°混合效果相差不大,说明扭旋角度的增加改善了混合速度。在最后一个元件的出口截面, 除了α=90°之外, 其他混合器径向H2SO4体积分数基本均匀。
2.3 混合特性定量分析
为了进一步地定量分析静态混合器的混合效果,通过采用分离强度来说明混合的均匀程度[8-9]。由式(2)计算得出混合器内元件进出口位置的分离强度。
不同扭角的混合器内特征轴向位置分离强度对比如图6所示。
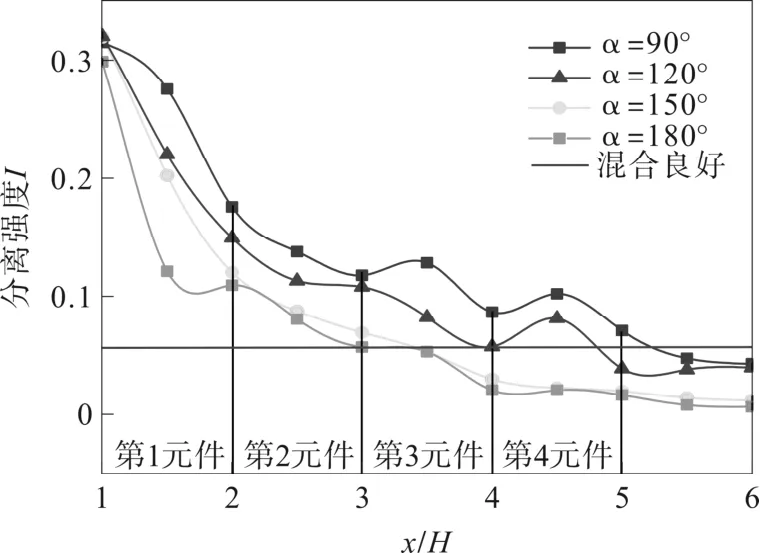
图6 分离强度随轴向位置的变化关系
由图6可以发现流体在经过第一个混合元件后,α=180°混合器的分离强度值迅速降低到0.11,混合效果非常显著,而α=90°的混合器则需要两个混合元件才能达到相同的分离强度。流体流经α=120°的混合器三个混合元件时,分离强度为0.0573,而α=180°只需要流经两个混合元件就能达到同样的分离强度值,相同条件下节省一个混合元件。α=150°的混合器与α=180°的混合器经过对比,经过第一个混合元件的分离强度值大于α=180°,即α=180°的混合器混合效果更好,第一个混合元件后混合性能相差不大;总之,α在 90°~180°时,混合效果随着扭转角度的增大而增大。
通过利用贡献率,进一步说明每一段混合元件对整个混合器混合效果的贡献程度[10]。贡献率表达式如下:

式中:Ii,m—第m个元件在入口截面的分离强度;
Io,m—第m个元件在出口截面的分离强度;
m—第m个混合元件。
根据式(3)可以计算得到四个混合元件的贡献率分别是 57%、24%、13%、6%。浓度相比主相较低的次相在第一个混合元件扭旋的作用下,便与主相充分混合,分离强度下降明显。随着第二个混合元件的继续作用,前三个混合元件对全部混合效果贡献超过90%。第四个混合元件对混合效应的贡献较低, 而且分离强度随轴向位移的变动较平缓,说明此时混合元件不再提升混合性能,而是起维持混合状态的作用。说明提高本文这种新型静态混合器的混合性能的有效途径为增大前三个元件的混合性能,可采用增加扭旋角的办法来实现。
3 结 论
在低雷诺数情况下,本文所提出的新型静态混合器内,扭旋角为 180°的混合器经过前三个混合元件的作用,混合效果明显优于其余三者。两相流体混合速度随扭旋角增大而增大,浓度分布更均匀;扭旋角的增大使得混合分离强度的降低速率增大,混合性能更优。适当地提高扭旋角参数有利于提高该静态混合器的混合性能。

