不确定度引起的瞳孔直径变化规律及其模型的研究

杨思琪，李 艳，郑金琳，于昊扬，罗二平,2，汤 池,2，武圣君，谢康宁,2

(空军军医大学：1军事生物医学工程学系军事医学装备与计量学教研室，2陕西省生物电磁检测与智能感知重点实验室，3军事医学心理学系，陕西 西安 710032)

我们生活在一个纷繁复杂的环境中，环境的波动给我们带来了各种形式的不确定性，比如可预期的不确定性和不可预期的不确定性，这些不确定性影响着我们的决策行为。我们是如何去感知这些不确定性的？有理论和实验表明大脑内部对于不确定度的表征与神经调质有关。YU等[1-2]研究认为，在学习和推断的过程中，乙酰胆碱表征的是可预测的不确定性，而去甲肾上腺素(norepinephrine，NE)表征的是不可预测的不确定性。什么影响了我们对不确定度的感知？ABERG等[3]研究发现焦虑的个体更容易受到不确定性的影响，导致其在决策过程中的表现不同。HMMERER等[4]研究发现老年人会高估不确定环境中的任务状态的可变性。KREIS等[5]的研究结果显示精神分裂症患者处理不确定性的神经环路出现了异常。SUTHAHARAN等[6]考虑到新型冠状病毒肺炎疫情暴发后给人们的生活带来更多的不确定性，认为在这种危机之下，人们会变得更加偏执多疑，而这种偏执心理可能与人们处理不确定性的方式有关。因此，探究大脑对不确定度的感知和处理在心理健康评估和脑认知功能研究方面具有重要的意义。

在实验研究方面，瞳孔直径的大小可以反映大脑内部的活动。蓝斑-去甲肾上腺素(locus coeruleus-norepinephrine，LC-NE)系统是一个重要的调节瞳孔直径的神经环路[7-8]，同时有研究表示LC-NE与大脑对不确定度的表征有关[1-2]。在计算建模方面，“贝叶斯大脑”的提出为建模大脑感知和学习的过程提供了一个框架。大脑被视为一个贝叶斯推断系统，基于其内部的模型对外部世界作出概率推断或预测。虽然已有研究表示，不确定度越高，瞳孔直径扩张越大[9]，但是其中具体的影响因素仍然处于讨论之中，比如在赌博任务中，由于输赢存在不确定性，其风险的大小会引起瞳孔直径的变化[10-11]；在决策任务中，奖赏的获得存在不确定性，其奖赏的大小与瞳孔直径的大小有关[12]；在序列任务中，罕见刺激发生的不确定性也会造成瞳孔直径的扩张[13]。

本研究从不确定度与信息量的角度对瞳孔直径的变化方面进行探究，记录受试者在含有不确定性的“卡牌预测任务”中瞳孔直径的变化，并构建隐马尔可夫模型(hidden Markov model，HMM)，计算出与蓝斑(locus coeruleus，LC)放电率的大小存在一一映射关系的预测误差。

1 对象与方法

1.1 对象

在空军军医大学招募16(男7，女9)名受试者参加瞳孔测量实验，年龄19～25(平均21)岁。所有参与者的视力正常或矫正到正常。受试者均被要求在实验前签署一份知情同意书。

1.2 方法

1.2.1 行为学范式 在卡牌预测任务中，一共设置有10张卡牌，数值从1到10。每次试验随机抽选两张卡牌，接着依次出现两张卡牌的数值。将第2张卡牌对应的具体数值简化为“大于第1张卡牌”或者“小于第1张卡牌”，受试者需要猜出试次中底牌的状态。卡牌预测任务中的不确定度主要表现在卡牌1出现之后，即如果卡牌1的值为1或10，则我们认为受试者能够非常确定卡牌2是否比卡牌1大，而如果卡牌1出现的是2、3、7、8等，则相对处于较不确定的状态，在5、6的情况下，则处于非常不确定的状态。

使用PsychToolbox-3[14]编写实验程序，共40个试次，分为8组，每组由连续出现的4个“1”和1个“5”构成，受试者首先看到卡牌1的数值，持续时间为5 s，然后受试者判断“卡牌2>卡牌1”或“卡牌2<卡牌1”，分别对应按下键盘上的数字1或2，记录受试者的反应时，接着屏幕上会显示卡牌2的数值以及受试者的选择是否正确，持续时间为5 s。

1.2.2 瞳孔数据采集及处理 实验是在一个亮度中等、光线稳定的环境中进行的。受试者佩戴降噪耳罩，以确保不被环境干扰。整个实验过程中，使用眼动追踪仪(aSeePro F100，七鑫易维，北京)以100 Hz采集数据，每次实验前均进行了双眼3点校准。在MATLAB(版本号:R2021a)中对左眼瞳孔直径数据进行预处理，步骤如下：①无效数据插值，眨眼期间的无效数据被眼动追踪仪配套软件记录为-1，使用-1前后的两点有效数据进行线性插值来替代；②数据清洗，舍去有尖峰或者波动特别大的伪迹，截取出有效试次；③归一化处理，为了便于在受试者内部和受试者之间进行比较，我们对每一试次的瞳孔直径进行归一化处理，即每一试次的瞳孔直径减去试次开始一段时间内的瞳孔直径的均值，并除以该值，从而得到瞳孔直径扩张的百分比的信号变化量。归一化处理可以降低外部环境刺激、疲劳等对结果产生的影响。

1.2.3 统计学分析 分别在卡牌1的值为1和5的情况下，使用MATLAB中的ttest函数对16名受试者在卡牌1出现后5 s内的瞳孔直径逐点进行配对样本t检验。

2 结果

2.1 行为学建模

在“贝叶斯大脑”的框架下，HMM模型被用来建模认知任务中的感知和推断过程。HMM由一系列离散的隐状态和观察值构成，使用贝叶斯网络来表示(图1)。在HMM中一次试验会依次出现不同的观察，观察出现的时间点用τ来表示，构成马尔可夫链。隐状态用Sτ来表示，取值为{s1,s2,s3...}，观察值用Oτ来表示，取值为{o1,o2,o3...}。从状态映射到观察值的似然p(oτ|sτ)用似然矩阵A来表示。从sτ-1转移到sτ状态的转移概率p(sτ|sτ-1)用状态转移矩阵B来表示。向量D为初始状态sτ=1的先验概率。当新的观察出现时，智能体更新其概率模型，先验和后验概率的差值被称为预测误差。

图1 HMM模型的贝叶斯网络表示

对卡牌预测任务构建HMM模型并进行计算(图2)。核心步骤如下：①参数初始化τ=2，其中B矩阵包含不确定度；②使用变分贝叶斯推断及消息传递计算预测误差的大小[15]，Sτ为后验概率，使用矩阵形式来表示(δ表示softmax函数)：

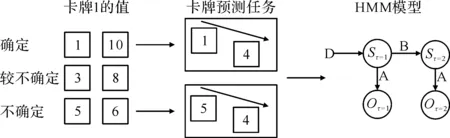
图2 卡牌预测任务实验范式及HMM模型

(1)

使用KL散度(DKL)来计算状态预测误差(State Prediction Error, SPE)，公式如下[16]：

(2)

③计算模拟的LC放电概率，预测误差值的大小与LC放电概率的映射关系通过一个logistic函数来转换。

2.2 不确定度的度量

1948年，SHANNON[17]将热力学中的熵引入信息论领域，即用熵来度量不确定度，记为信息熵(E)。在某一状态下的不确定度越高，其信息熵越大；相反，如果某一状态非常确定，则此时的信息熵接近于0。在另一方面，信息熵也表征了概率分布的均匀程度，即越接近于均匀分布，信息熵越大。设随机变量为X，事件{X=xi}发生的概率表示为p(xi)。信息熵为信息量的期望，公式为：

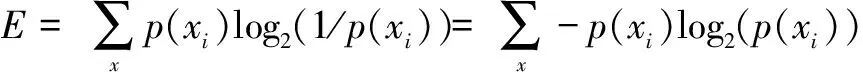
(3)

对卡牌1从1到10的10种情况分别计算信息熵。在卡牌1值为5或6时，两种情况的分布接近于均匀分布(概率为4/9和5/9)，信息熵具有最大值；而在卡牌1值为1或10时，信息熵具有最小值(表1)。

表1 卡牌1出现后不同状态的概率和信息熵

2.3 不确定度与瞳孔直径

在卡牌预测实验中，当卡牌1值为5时，即不确定状态下(红色的线条)受试者的瞳孔直径的扩张大于卡牌1值为1时，即确定状态下(蓝色的线条)瞳孔直径的扩张。对每一个时间点的数据做配对样本t检验，灰色的星号(*)表示在该时刻P<0.05，差异具有统计学意义(图3)。

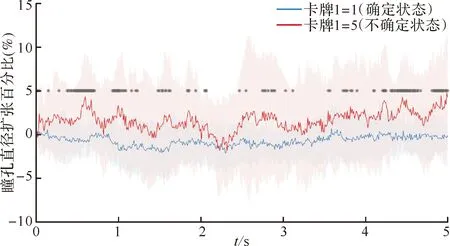
图3 卡牌预测任务的瞳孔直径

2.4 不确定度与模拟LC放电率

如图4A所示，当卡牌预测任务中卡牌1的值为1时对应的是不确定的状态，值为5时对应的是确定的状态。图4B的结果显示在任务中不确定度增高时，预测误差也相应增加。在图4C中可以观察到模拟LC的两种放电模式——一种为规律性的、持续时间长的、紧张性放电模式，一种为簇发的、短暂的、相位性放电模式，其中密集发放的相位性放电对应于图4B中出现高不确定度的位置。

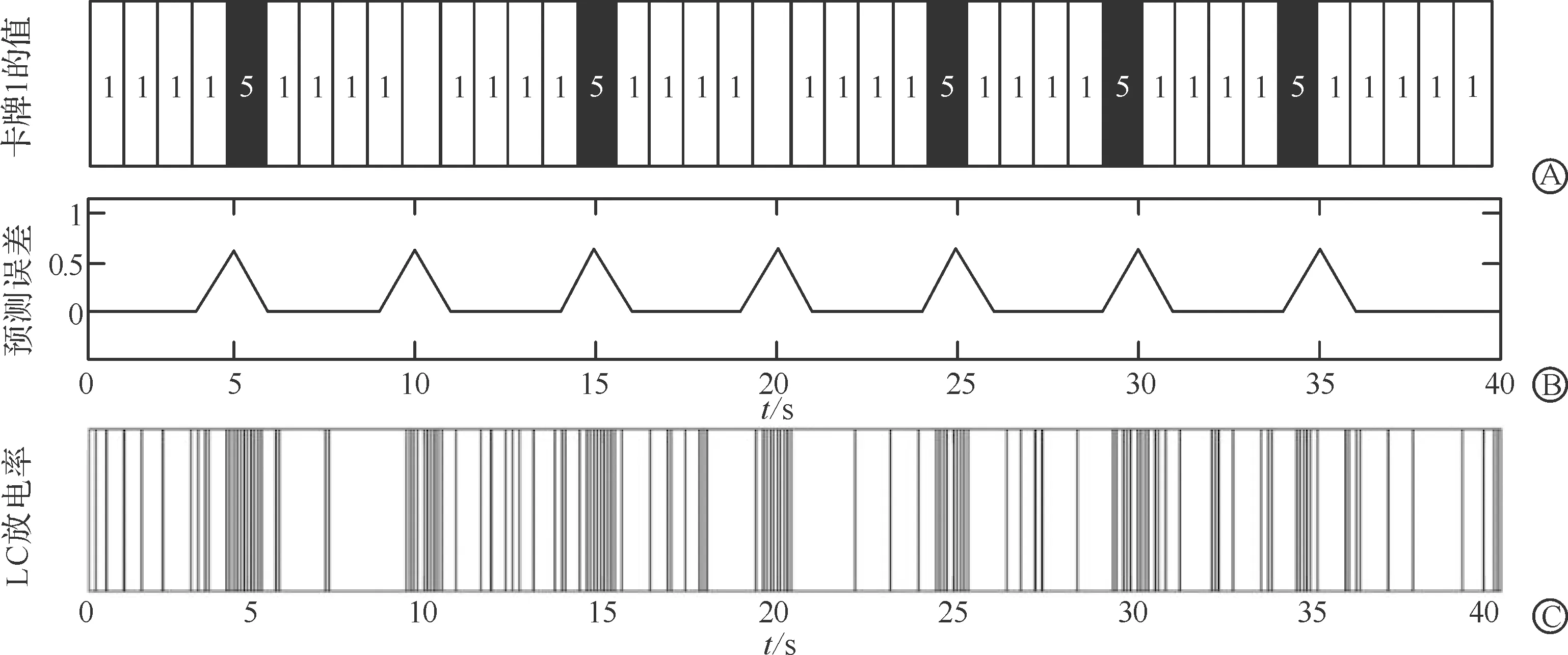
A：40次试验中卡牌1的值，值为1时表示确定的状态，值为5时表示不确定的状态；B：不同不确定度下对应的预测误差；C：不同不确定度下对应的LC放电率，每秒钟划分为10个格子，每个格子出现发放的概率等于将计算出来的LC放电概率。

分别对1～10的10张卡牌计算其信息熵、对应的预测误差及LC放电概率，其中信息熵用来度量不确定度。结果如图5所示，预测误差和LC放电概率随着信息熵的增加而增加，随着信息熵的减少而减少。

图5 卡牌预测任务的信息熵、预测误差与LC放电概率

3 讨论

本研究记录了共16名受试者在不同不确定度的任务下真实瞳孔直径的变化，并建立了不确定度引起瞳孔直径变化的HMM模型，对大脑如何表征不确定度进行了探究。本研究主要的建模和实验结果发现：①眼动追踪实验研究中受试者的瞳孔直径在环境不确定时变大，表明大脑内部对不确定度进行响应，并通过LC-NE神经环路的控制使瞳孔表现出扩张；②通过对“卡牌预测任务”构建HMM模型，计算了由于不确定性造成的预测误差。在越不确定的情况下，当前状态的信息熵越大，此时智能体的预测误差值也越大，并且预测误差对应着模拟的LC出现相位放电模式。

在不确定的环境中，本研究受试者表现出瞳孔直径扩张的结果与前人对不确定度的研究结果一致[5,12]，但相较于其他针对不确定性的刺激造成信息量下降进行讨论的研究，本研究着重讨论的是处于一个高不确定度的状态，在这样的状态下信息量很大，前者对应的是变化量，而后者是状态量。有的研究将不可预期的、不确定度中的环境波动细分出来讨论[18-19]，我们指出对环境波动的度量可能同样可以使用信息熵来表示，从而通过信息熵将不同划分方式的不确定度统一起来，讨论其背后的计算机制。

在模型方面，相较于近几年研究较多的主动推断模型[20]——对感知、学习和决策建模的部分可观测马尔可夫过程，本研究中所讨论的任务不包含学习和主动选择的部分，但我们指出这些结果适用于进一步复杂化这些任务时建模智能体对外部世界的积极响应，比如分析Go-Nogo或是Explore-Exploit等任务中信息熵的大小及不确定度的作用。

综上所述，本研究提示大脑对于不确定度的表征是通过LC-NE系统跟踪到不确定性造成的预测误差来实现的，大脑对不确定度的表征同时也是对信息量的表征。