基于空间结构的杉木枝下高可视化模拟研究

朱念福，张怀清*，崔泽宇，杨廷栋，李永亮，刘 华

(1.中国林业科学研究院资源信息研究所，北京 100091；2.国家林业和草原局林业遥感与信息技术重点实验室，北京 100091)

枝下高是指树冠第一个活枝距离地面的高度，是反映树木生长活力和冠形特征的重要指标[1-2]。目前林木生长可视化模拟主要包括结构功能模型对不同发育阶段的单木细节形态模拟[3-5]，以及基于林木生长模型和三维渲染模拟等形式[6-12]，仅通过树木模型整体的伸缩和替换来实现，均未考虑枝下高自身的变化规律，无法很好体现林木形态的差异性，也无法表现林木生长过程中枝下高的动态变化。

目前，国内外学者对枝下高模型研究中主要考虑单木因子(树高、胸径等)、林分统计因子(林分断面积、冠幅竞争因子等)和立地指数对枝下高的影响[13-19]。如Ritchie等[15]以冠幅竞争因子、林分断面积和立地指数等预测变量，构建了美国太平洋西北地区14个树种的枝下高模型；Rijal等[17]引入树木尺度因子和竞争因子，构建了北美阿卡迪地区13个树种的枝下高模型；马载阳等[20]构建了湖南省黄丰桥国有林场的杉木枝下高模型；卢康宁[21]分析了杉木分枝生物量与分枝结构的关系，构建与分枝轮数有关的杉木枝下高模型，这些模型均需要林木分枝的生长轮数和年龄信息支持，未考虑林木空间结构对枝下高的影响。枝下高变化主要通过自然整枝实现，除了自身因素，还受周围环境竞争影响，而对象木与其邻近木组成的空间结构对林木生长和自然整枝具有较大影响[22-25]。

本研究以杉木(Cunninghamialanceolata)人工林为例，考虑林木自身属性(胸径、树高等)和林木所处空间结构单元对枝下高的影响，构建出基于空间结构的枝下高模型。应用林分三维模型实时生成方法，构建出枝干可控的杉木三维模型。根据单木初始胸径，通过单木胸径连年生长量模型、树高曲线模型、冠幅面积估计模型和考虑空间结构的枝下高模型拟合林木生长状态，结合Unity3D渲染引擎，最终实现杉木枝下高的可视化模拟。

1 材料与方法

1.1 试验区概况

试验区位于湖南省攸县黄丰桥国有林场(113°04′～113°43′E，26°43′～27°06′ N)，平均气温17.8 ℃，年均降水量为1 410.8 mm，无霜期292 d，年平均日照时间1 612 h，属于亚热带季风湿润气候。地貌以丘陵、山地为主，境内最高海拔1 270 m，最低海拔115 m，坡度一般为20°～35°。森林覆盖率90%以上，树种以杉木、松类为主。

1.2 数据来源

采用常规的测树方法，使用卷尺测量胸径(DBH)，使用测高杆测量树高和枝下高(HCB)，使用塔尺测量冠幅(CW)，利用全站仪测量样地内杉木的相对位置坐标(X,Y,Z)。根据2012年调查数据，选取地位指数[25]相同的6块杉木人工林临时样地，共计2 498组。调查数据按照3∶1的比例随机划分拟合数据(1 874组)和检验数据(624组)。样地核心区(距边界5 m)属性分布如表1所示。

表1 样地数据统计量

1.3 空间结构因子构建

根据惠刚盈等[24]提出的最佳空间结构单元，选择最近4株邻木参与空间结构因子的构建，本研究构建了3个空间结构因子：水平空间结构参数、垂直空间结构参数和空间结构单元平均距离。

1.3.1 水平空间结构参数

在水平空间维度，对象木主要受到邻近木的冠幅挤压[26-27]。邻近木的冠幅挤压抑制了对象木的树冠生长,促进对象木自然整枝。而且同样程度的冠幅挤压，对于不同大小林木的影响是有差异的[28]，可以用邻近木与对象木胸径的比值来反映这种差异。据此建立表示对象木受最近4株邻木冠幅挤压的水平空间结构参数PHi(图1A)，表达式如下：

(1)

式中：Cwi为对象木i的冠幅；Cwj为邻近木j的冠幅；Dj为邻近木j的胸径；Di为对象木i的胸径；dij为对象木i与邻近木j的水平距离，n为邻近木株数，n=4。

1.3.2 垂直空间结构参数

在垂直空间维度，由于邻近木的上方遮盖，抑制了对象木的生长，促进对象木自然整枝[23]。据此建立表示对象木受最近4株邻木上方遮盖的垂直空间结构参数PVi(图1B)，表达式如下：

(2)

式中：Hj为邻近木j的树高；Hi为对象木i的树高；ΔZ为邻近木j与对象木i的空间位置高度差。

1.3.3 空间结构单元平均距离

已有研究表明林分密度对枝下高有较为显著的影响[29]，因此对象木与邻近木之间的距离显然对对象木的枝下高有影响。据此建立表示对象木与最近4株邻木的空间结构单元平均距离(dDISi)(图1C)，表达式如下：

(3)

1.4 模型选择

本研究选择5个常用枝下高(HCB)与树高(H)、其他变量(X)的关系模型作为候选基础模型，各模型表达式见表2。

表2 枝下高模型

树高和胸径是预测枝下高最重要的两个变量[13,19]。因此，本研究首先拟合只含树高和胸径变量的枝下高模型，选出最优的枝下高基础模型。本研究构建的空间结构参数表示了林木受到邻近木的竞争影响，一定程度上可以作为竞争因子。考虑竞争因子在常用枝下高模型中的表达形式，将空间结构因子线性加入所选择的枝下高基础模型中，选取综合指标较好的枝下高模型。考虑空间结构的枝下高模型表示如下：

(4)

式中：HCB为枝下高，DBH为胸径，f(H,X)为枝下高模型表达形式，H为树高，X为除树高外其他变量，Y为空间结构因子及组合，a、b、c、c1、c2、c3为方程参数。然后通过调查数据进行拟合和检验，最终选出综合指标较好的因子构建考虑空间结构的枝下高模型。

1.5 模型评价与检验

本研究采用决定系数(R2)、估计值的标准差[SEE，式中记为σ(SEE)]进行模型评价；采用平均误差[ME,式中记为σ(ME)]，平均绝对误差[MAE，式中记为σ(MAE)]、总相对误差[TRE，式中记为σ(TRE)]和平均系统误差[MSE，式中记为σ(MSE)]进行模型检验[30]。其中，R2和SEE是回归模型的最常用指标，反映了模型的拟合优度。TRE和MSE是反映拟合效果的重要指标，二者都应该控制在一定范围内(如±3%或±5%)。6个指标的具体计算公式如下：

(5)

(6)

(7)

(8)

(9)

(10)

1.6 枝下高模拟

为了表示杉木枝下高的变化，除了本研究需要构建的枝下高模型，还使用了其他研究在同一区域拟合得到的3个相关杉木生长模型：单木胸径连年生长量模型、树高曲线模型、冠幅面积估计模型。单木胸径连年生长量模型[31]表示如下：

(11)

树高曲线模型[32]表示如下：

(12)

冠幅面积估计模型[33]表示如下：

CWa=DBH/(2.861 7-0.034 98DBH)。

(13)

式中：t为时间；RS为相对植距；RD为相对优势度；SI为地位指数；H为树高，DBH为胸径，CWa为冠幅面积。

李永亮等[34]基于林分三维模型实时生成方法，构建了林分中形态各异的杉木三维模型，且三维模型的干、枝和叶是分离的，较好地表现了林分中杉木的形态结构，但无法表现杉木枝下高的变化。

本研究仅构建树干和树枝分离的杉木三维模型，使用上述方法实现林分三维模型构建，实现枝下高动态调整功能。使用下述方法模拟树干和枝干的变化。

1)树木胸径：

DTrunk2=DTrunk1+fD(DTrunk1)。

(14)

式中：DTrunk2为下一时刻的树木胸径，DTrunk1为当前时刻的树木胸径，fD(DTrunk1)为单木胸径连年生长量模型拟合的胸径变化量。

2)树木树高：

HTrunk2=fH(DTrunk2)。

(15)

式中：HTrunk2为下一时刻的树木树高，fH(DTrunk2)为树高曲线模型拟合的杉木树高。

3)枝干高度：

HCB2=fHCB(HTrunk2,DTrunk2);

(16)

HBranch2i=HCB2+(HBranch1i-HCB1)·(HTrunk2/HTrunk1)。

(17)

式中：HCB2为下一时刻枝下高，HCB1为当前时刻枝下高，fHCB(HTrunk2,DTrunk2)为枝下高模型拟合的枝下高，HBranch2i为下一时刻树枝i的高度，HBranch1i为当前时刻树枝i的高度，HTrunk1为当前时刻树木树高。

4)枝干长度：

CW2=fCW(DTrunk2);

(18)

LBranch2i=LBranch1i·(CW2/CW1)。

(19)

式中：CW2为下一时刻冠幅，CW1为当前时刻冠幅，fCW(DTrunk2)为冠幅面积估计模型拟合的冠幅，LBranchi2i为下一时刻树枝i的长度，LBranch1i为当前时刻树枝i的长度。

5)枝干基径：

DBranch2i=DBranch1i·(CW2/CW1)·(HTrunk2i/HBranch2i)。

(20)

式中：DBranch2i为下一时刻树枝i的基径，DBranch1i为当前时刻树枝i的基径。

2 结果与分析

2.1 枝下高模型选取和检验

最初拟合只含H和DBH为变量的枝下高模型，选择最优的枝下高基础模型。枝下高基础模型的参数估计值、拟合优度和检验结果见表3。

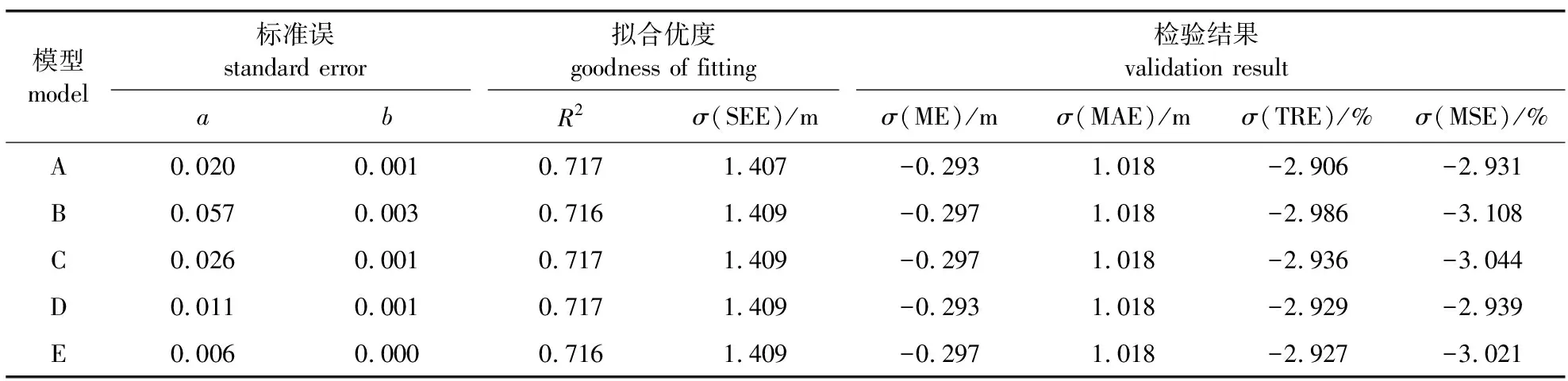
表3 枝下高基础模型的拟合优度及检验结果

由表3可知，5个模型的参数估计值标准误均较小，说明模型各参数的稳定性较好。5个模型的相关系数(R2)相差不大，均在0.717左右，估计值标准差SEE为1.40～1.41 m。5个模型检验结果区别不明显，所有模型的平均误差(ME)为-0.29～-0.30 m，平均相对误差(MAE)均小于1.02 m，总相对误差(TRE)为-2.90%～-3.00%，平均系统误差(MSE)为-2.90%～-3.20%。其中，模型A的总相对误差(TRE)和平均系统误差(MSE)均最小，分别为-2.906%和-2.931%，平均误差(ME)也较小，为-0.293 m，且模型A的表达形式相对简单，符合生物学意义，因此选用模型A作为加入空间结构参数的枝下高基础模型。

将空间结构因子加入模型A中，空间结构因子及其组合对应的拟合优度和模型检验结果见表4。由表4可知，加入空间结构因子后，枝下高模型的拟合优度得到了提升，各模型检验指标减小。其中PV、PH和dDIS对枝下高模型拟合效果的提升依次减小。加入的空间结构参数越多，对枝下高模型的拟合优度提升越大，同时，枝下高模型变得越复杂。

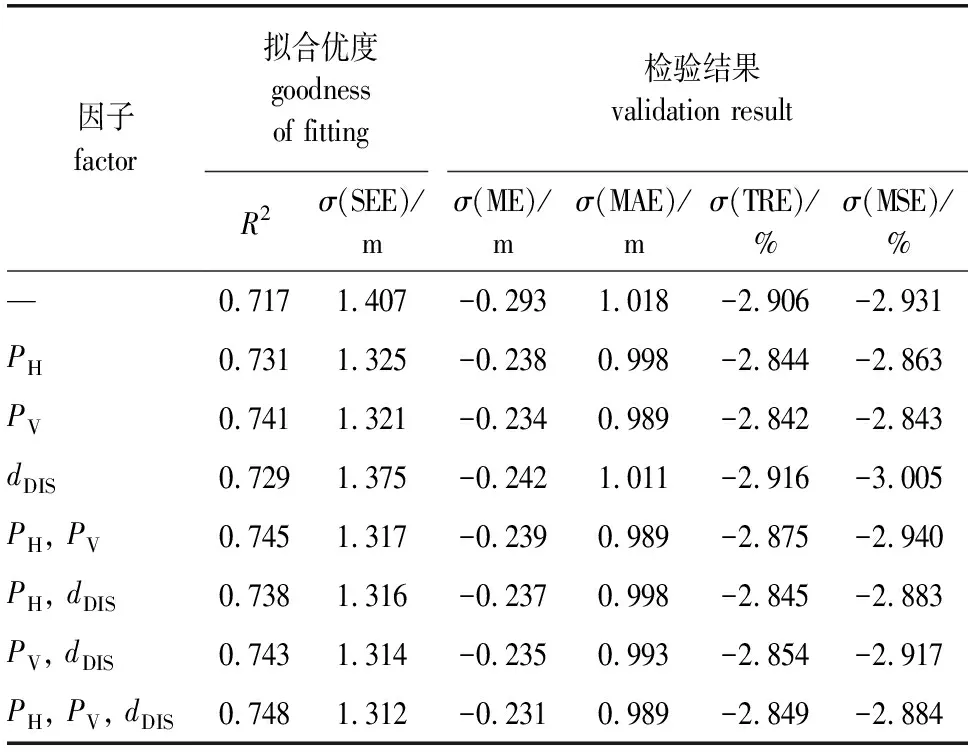
表4 加入空间结构参数的枝下高模型拟合优度及检验结果

实际上，构建的3个空间结构参数是从不同角度分析对象木受邻近木的竞争影响，本质上都是反映周围林木与对象木对阳光和生长空间的竞争。考虑到模型中的变量越少越便于应用，因此，选择影响效果较为明显的垂直空间结构参数PV，枝下高模型的R2从0.717提升到了0.741，σ(SEE)从1.407 m减小到了1.321 m,σ(TRE)和σ(MSE)均在±3%范围内。最终建立的枝下高模型如下所示：

HCB=H/[1+exp(0.046 42-0.000 21DBH-0.237 22PV)]。

(21)

根据枝下高模型的预测值，绘制残差分布图(图2)，由图2可知，残差的散点随机分布，模型拟合效果较好。

2.2 杉木枝下高模拟

选择调查数据，利用胸径连年生长量模型获取每年的胸径数据，利用树高曲线模型获取树高数据，冠幅面积估计模型获取冠幅数据，利用枝下高模型获取枝下高数据。

根据林木当前状态，拟合10年后、20年后林木的生长状态。为了方便观察，显示基于前5条数据构建的杉木枝下高数据，并选取其中编号1～5号的数据(表5)。由表5可知，枝下高与树高相关性较高，树高较高的杉木，其枝下高也较高，且杉木受到垂直方向上的遮盖越严重，其枝下高也越高。

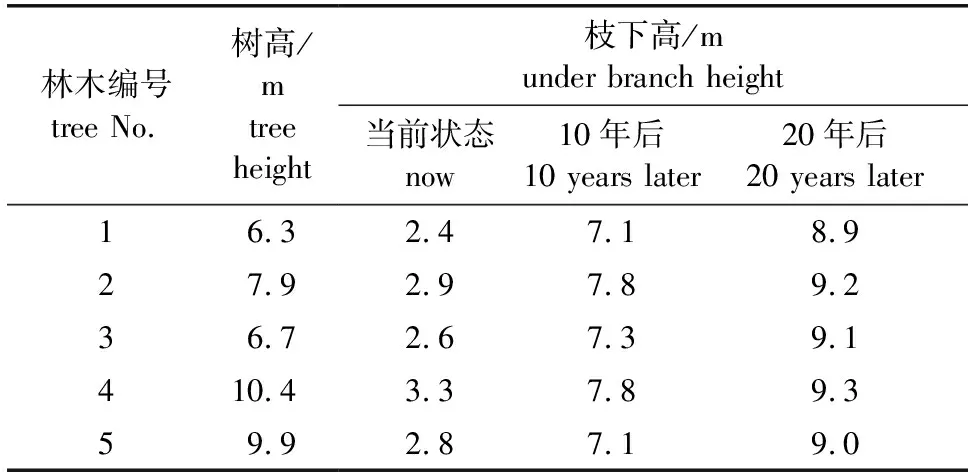
表5 枝下高预测数据

3 讨 论

林木除了受自身因素调控，还受外部环境影响，而林木属性(树高、胸径、冠幅、枝下高等)则是这些影响因素综合作用的结果。树高和胸径是描述林木健康状况的两个重要属性，与枝下高息息相关[35]，一定程度上可以反映枝下高与林木自身因素的关系。枝下高与外部环境的关系则可以通过立地指数、林分密度等统计因子、林分空间结构参数等来表征，但本质上是反映林木间竞争的优劣程度[26]。与类似研究相比[1-5,13,19]，本研究构建的枝下高模型参数少，拟合精度稍低：一是因为样地较少，不能提供完整的林分统计信息；二是因为在数据预分析阶段，发现与距离无关的竞争因子等林分因子对枝下高模型并无明显改善，且林分因子在生物学上的解释性较差。实际上，林木主要受周围几株邻近木的竞争影响，考虑林分空间结构单元对林木枝下高的影响更为直接。

本研究的枝下高模型仅与林木自身属性和林木所处空间结构单元有关，无需调查较大范围内的所有林木信息，便于在样地状况复杂、无法全面调查林木数据时，能够基于较小范围内的空间结构单元，获得受竞争影响的枝下高数据。

在枝下高可视化模拟中，本研究基于一期数据预测了枝下高未来10年和20年后的状态，由于没有真实数据进行对比，因此无法对模拟结果的准确性进行检验。但枝下高模型反映了杉木林分中枝下高与树高、胸径和垂直空间结构参数的关系，其中垂直空间结构参数是基于对象木和相邻木的树高得来的，因此在胸径、树高模型拟合效果较好的基础上，枝下高模型的预测准确性在可接受的范围内。结合他人研究的杉木生长模型，实现了杉木枝下高可视化模拟，效果较为逼真，更符合现实。

为了提高杉木枝下高模型的预测精度，在今后的外业调查中可以考虑利用大区域的多个样地进行研究；由于林木胸径和树高具有极为显著的相关性，因此联立树高模型和枝下高模型，形成仅与胸径和林木距离相关的枝下高模型是今后研究的方向。