概率易错题面面观
文/刘宇峰

忽视等可能性
例1把3颗算珠放在计数器的3根插棒上构成一个数字,例如,图1摆放的算珠表示数300。现将3颗算珠任意摆放在这3根插棒上。求构成的数是三位数的概率。
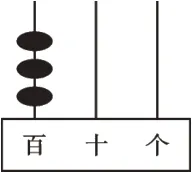
图1
【错解】3颗算珠,3根插棒,我们将数字一一有序列举出:
情况1:将3颗算珠放百位上,只有一种结果,表示数300;
情况2:将2颗算珠放百位上,剩下1颗有两种放法,放在十位上,表示数210,或放在个位上,表示数201;
情况3:将1颗算珠放百位上,剩下2颗有三种放法,都放在十位上,表示数120,或都放在个位上,表示数102,或十位、个位上各放一个,表示数111;
情况4:百位上不放,有四种放法,3颗算珠都放在十位上,表示数30,或十位上放2颗,个位上放1颗,表示数21,或十位上放1颗,个位上放2颗,表示数12,或都放个位上,表示数3。
共有10种结果,其中构成三位数的结果有6种,所以构成的数是三位数的概率是
【分析】错解一一有序地列举出构成的数字,初看似乎有道理,但细细研究,我们不难发现,这10种结果不具有等可能性。
【正解】将3颗算珠任意摆放在计数器的3根插棒上,等价于:有3颗算珠,首先放第一颗算珠,它可以放在百位上,可以放在十位上,也放在个位上,有3种等可能放法;接着放第二颗算珠,同样,它可以放在百位上,可以放在十位上,也放在个位上,也是有3种等可能放法;最后放第三颗算珠,它同样有3种等可能放法(百位、十位、个位),画树状图如下:
将3颗算珠任意摆放在这3根插棒上,共有27种等可能的结果,其中构成的数是三位数的结果有19种,所以构成的数是三位数的概率为
【点评】求概率的前提条件是“等可能性”。一般地,设一个试验的所有可能发生的结果有n个,它们都是随机事件,每次试验有且只有其中的一个结果出现。如果每个结果出现的机会均等,那么我们说这n个事件的发生是等可能的,也称这个试验的结果具有等可能性。
未能区分“有放回”与“不放回”
例2为了调动同学们学习数学的积极性,某班组织开展了“数学小先生”讲题比赛,老师将四道备讲题的题号1、2、3、4分别写在完全相同的4张卡片的正面,将卡片背面朝上洗匀。小明随机抽取两张卡片,用画树状图或列表的方法求两张卡片上的数字是“2”和“3”的概率。
【错解】列表如图。
共有16种等可能的结果,其中两张卡片上的数字是“2”和“3”的结果有2种,
所以小明随机抽取两张卡片,两张卡片上的数字是“2”和“3”的概率为
【分析】随机抽取两张卡片,相当于先后抽两次,第一次抽到的卡片不放回,再抽第二次。
【正解】列表如图。
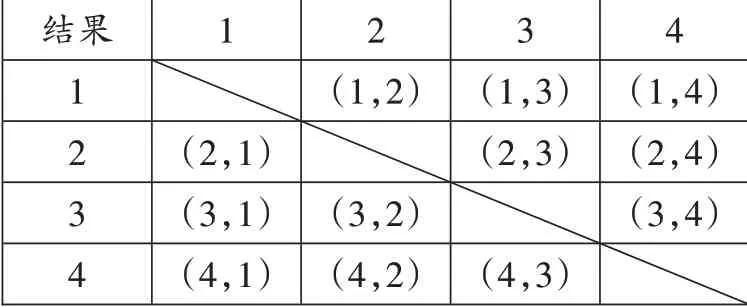
结果1 2 3 4 1(2,1)(3,1)(4,1)2(1,2)(3,2)(4,2)3(1,3)(2,3)(4,3)4(1,4)(2,4)(3,4)
共有12种等可能的结果,其中两张卡片上的数字是“2”和“3”的结果有2种。
所以小明随机抽取两张卡片,两张卡片上的数字是“2”和“3”的概率为
【点评】对于“抽卡片”“摸球”等类型的问题,我们要看清题目条件的叙述是“有放回”还是“不放回”。对于“有无放回”,一是题目条件中明确交代是“有放回”,二是同时“抽”“摸”两次,即暗示“无放回”。“掷骰子”“抛硬币”“摇转盘”等类型的问题,第一次出现的,第二次还有可能出现,相当于“抽”“摸”中的“有放回”。

