客流视角下轨道交通网络动、静态脆弱性分析

陈亚雄，徐 博，霍非舟，姚 康，吕 龙

(1.武汉理工大学 安全科学与应急管理学院，湖北 武汉 430070；2.武汉理工大学 中国应急管理研究中心，湖北 武汉 430070；3.中南大学 商学院，湖南 长沙 410083)

轨道交通具有运载能力强、速度快、准确性强、能源消耗低等优点，广泛应用于国内外各大、中型城市，截止2021年12月，我国已有50个城市建成了轨道交通，轨道交通出行已成为我国一、二线城市的居民日常出行的主要交通方式。复杂网络是一种拥有大量节点，同时节点之间存在着复杂的结构联系的网络，而轨道交通网络作为一种典型的复杂网络，不少研究人员都采用复杂网络相关理论对城市的交通与网络的各项性质与特点进行研究。

部分研究人员将复杂网络理论应用在城市轨道交通的应急选址问题上，徐佩佩等[1]采用Space L、Space P与Space R的方法将轨道交通网络拓扑化，将路网信息变为复杂网络的节点选取问题；冉连月等[2]利用pajek软件对武汉市轨道交通线进行网络中心性分析，并通过复杂网络的理论与“P-中心”选址模型，构建了武汉市轨道交通线网的应急救援站选址模型；丁坤迪等[3]通过灰色关联分析方法，构建无水港选址问题的复杂网络节点重要性评价指标体系，并通过对部分参数进行灵敏性分析，寻找出无水港的最佳位置；卢弋等[4]根据轨道交通网络中的站点的建设规模、故障发生频次等数据，结合复杂网络的特点，通过集合覆盖模型，建立了轨道交通中应急点的选址模型；罗星等[5]运用空间句法构建成都市轨道交通换乘站点选择模型，在传统换乘站点研究中，加入不对称值、深度值、可达性指标等考虑因素，为成都市轨道交通的换乘节点选择问题提供了优化思路；王希良等[6]通过复杂网络的互信息理论，构建出轨道交通的有向复杂网络，并通过信息量与重要性指标的计算，获取轨道网络的脆弱性节点。

部分研究通过复杂网络的相关理论从复杂网络脆弱性的角度研究交通网络的特点，通过分析交通网络中客流轨迹变化，运用计算机仿真的方法对交通网络进行脆弱性分析研究。WANG等[7]通过复杂网络的方法构建了轨道交通拓扑模型，并根据大客流效应下的轨道网络脆弱性仿真结果，给出了大客流运营下轨道交通脆弱性提升建议；MA等[8]通过分析城市平均最短路径、拥挤度以及平均客流强度，构建出城市脆弱性评价方法，并采用计算机仿真的方式模拟出城市脆弱性的关键节点；LIU等[9]考虑到出行成本和出行方式变化对复杂网络中客流人数分配的影响，构建了基于客流出行习惯的轨道交通网络脆弱性分析模型；曲迎春等[10]通过对比地铁单层网络与公交-地铁双层网络遭遇紧急情况后，北京、深圳两地轨道交通的出行的失败率与出行时间增加率来验证公交-地铁双层网络的稳定性，通过构建双层网络解决大型城市的交通网络脆弱性问题；许葭等[11]在传统轨道的网络脆弱性分析过程中开创性地加入了地铁网络事故蔓延机理的元素，构造出轨道交通网络中的地铁网络事故蔓延引力模型，解决了轨道交通等复杂网络在客流事故中的应急响应问题；YU等[12]通过Space P的复杂网络拓扑方法与旅行时间模型构建轨道交通的复杂网络模型，通过轨道交通站点间网络流量效率与客流效率来分析轨道交通布局问题，为轨道交通的布局合理化提出相应建议；叶青[13]采用Space L模型构建了重庆市轨道交通的拓扑网络，通过复杂网络理论分析重庆市轨道交通的基础指标与分布规律，并通过蓄意攻击的方法进行网络脆弱性分析，鉴定对网络效率影响最大的轨道站点；GUO等[14]采用有向加权网络解决实际项目中的复杂网络脆弱性节点问题;李成兵等[15]采用站点映射法建立呼包鄂城市群的道路-轨道复合网络，对比单一运输方式下的交通网络，发现通过对复合网络关键点和线路的保护，可快速降低城市交通网络的失效风险。

笔者在传统的复杂网络相关理论的基础上，采用计算机模拟仿真对比蓄意攻击与随机攻击后，轨道网络的度、介数、网络直径、平均路径长度、平均聚类系数等静态网络脆弱性指标，量化蓄意攻击对静态网络脆弱性的危险性；在传统的静态网络脆弱性基础上，结合弗洛伊德算法计算每个站点遭受攻击后在不同出行距离系数d下的可达站点数目与占比，量化不同类型的轨道交通站点遭遇攻击后对轨道交通网络动态脆弱性的影响，使得网络脆弱性研究更加完整。并结合各地区轨道交通的实际线路设计，快速解决轨道交通网络中应急救助站的选取工作与网络节点脆弱性评价等现实问题。

1 轨道交通网络模型构造与动静态指标构建

1.1 复杂网络基本理论

复杂网络统计指标包含度、介数、网络直径、平均路径长度、平均聚类系数[16]。

(1)度。节点的度被定义为该节点与网络中其他节点间的连线数量，网络中的节点与其他节点连接越密切，意味着节点的度值越大，而网络的平均度值为网络中所有节点度值的平均值。

(2)介数。节点的点介数被定义为网络中包含节点V的最短路径数量与网络中所有最短路径数量的比值。由于网络中信息一般是通过最短路径传播的，所以通过该节点的最短路径占比反映出该节点在网络中信息传递的重要性。

(3)网络直径。网络直径被定义为网络中所有节点对连线距离中的最大数值，网络直径越大的网络在信息传递途中的损耗也会相应增加。

(4)平均路径长度。网络的平均路径长度被定义为网络中任意两节点对间最短距离的平均值，可以反映出复杂网络的尺寸规模。

(5)平均聚类系数。聚类系数数值被定义为节点i在网络中与周围节点的实际连线数量与连线的理论最大值的比值，通常用来描述网络中节点间疏密关系的程度。对于节点i而言，在网络中与ki个节点相连，节点i周围至多可能存在的边数ni，如式(1)所示。

(1)

Ei表示i与ki个相邻节点之间实际存在的连边数量，网络节点i的聚类系数Ci如式(2)所示。

(2)

1.2 静态网络脆弱性分析分析

轨道交通网络的脆弱性目前主要采用最大连通子图的相对大小及网络效率2个指标进行计算。

(1)最大连通子图。当城市轨道交通网络受到攻击后，网络有可能被分隔为不能互相交流的子网络，所有子网络中节点数值最大的网络个体即为最大连通子图。最大连通子图所受攻击影响最小，路网的连通性较好，最大连通子图如式(3)所示。

(3)

式中：NE为最大连通子图的节点数目；NO为初始网络中节点数目。

(2)网络效率。网络效率一般作为网络中节点间信息的交换效率的评价标准，在城市轨道交通路网中可以反映乘客到达目的地的方便程度。可用网络平均效率指标来表示城市轨道交通网络的效率脆弱性。两点之间的效率eij由网络G的节点对(i,j)之间的距离的倒数定义，如式(4)所示。平均网络效率E如式(5)所示。

(4)

(5)

1.3 动态网络分析

在传统的静态网络分析的基础上，引入客流出行因素，以乘客出行距离系数作为阈值，分析动态场景下轨道交通网络遭受攻击后保障出行的稳定性。da值为网络遭受攻击后乘客所在站点i与目的地站点j之间的出行时间,do为乘客所在站点i与目的地站点j之间的原始出行时间，出行距离系数d如式(6)所示。

(6)

出行距离系数的阈值为dk，当意愿系数d≤dk时，i站点乘客在轨道交通网络遭受攻击后仍可到达目的地站点j；反之不可到达目的地站点j，如式(7)所示。

(7)

i点乘客在j点遭遇攻击后，距离系数dk阈值下可达的地点占比如式(8)所示。

(8)

可达的乘客人数如式(9)所示。

(9)

整个轨道系统在聚力系数dk阈值下，当j点受到攻击后，系统可达地点占比如式(10)所示。

(10)

整个轨道系统可达人数占比如式(11)所示。

(11)

其中，ωi为i点的出行人数。

2 沈阳市轨道交通网络脆弱性分析

沈阳地铁运营线路共有4条，分别为：1号线、2号线、9号线、10号线，共设立地铁站85座，其中换乘点7个。采用Space L构建沈阳市地铁网络拓扑图，如图1所示。

图1 沈阳市地铁拓扑图

通过pajek软件构建沈阳地铁网络图，通过matlab软件计算复杂网络的特征指标项，可得沈阳地铁网络基本属性的特征指标值，如表1所示。

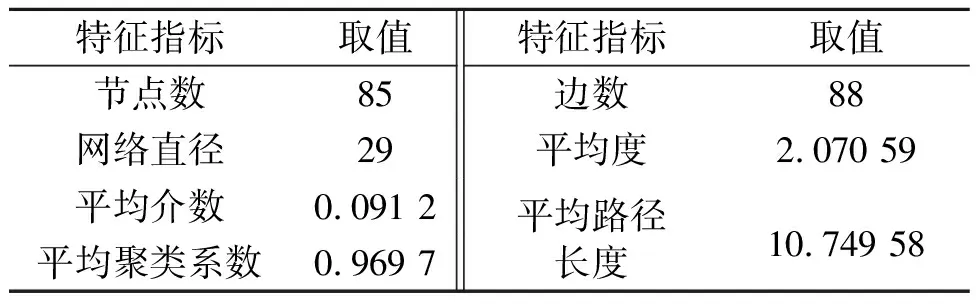
表1 沈阳地铁网络基本属性的特征指标值

2.1 静态脆弱性分析

2.1.1 攻击策略

通过复杂网络的度、接近中心性和介数的参数对复杂网络节点重要性进行评估[17]，针对评估后较为重要的节点，采用蓄意攻击与随机攻击两种攻击策略，验证节点的重要性。

(1)蓄意攻击。郭露露等[18]应用复杂网络理论对北京地铁网络进行脆弱性评估，通过对比随机攻击和蓄意攻击运输能力损失，发现运输能力损失最严重的均为换乘车站，换乘车站为轨道交通网络中最脆弱的节点，因此换乘车站应该重点防护。

对于沈阳市轨道交通采用加权初始度数攻击策略，即对初始网络按照节点或边度的加权大小为依据移除相关节点或边。根据沈阳日报2020年6月11日新闻公布，沈阳地铁10号线开通后各线路日均客运量分别为：1号线日均客运量27.63万人次/日，2号线日均客运量23.41万人次/日，9号线日均客运量12.76万人次/日，10号线日均客运量8.23万人次/日，网络日均客运量72.03万人次/日。根据新闻数据可计算得到1、2、9和10号线的平均每站人数分别为1.256万人、0.9万人、0.558万人、0.392万人，可得到沈阳市7个度值为4的轨道交通换乘点根据站点人数从多到少依次排序为：V17(青年大街)、V12(铁西广场)、V21(傍江街)、V43(奥体中心)、V34(中医药大学)、V49(淮河街沈医二院)、V67(长青南街)，并根据顺序依次进行攻击。

(2)随机攻击。为对比蓄意攻击对沈阳市地铁脆弱性的影响结果，采用随机攻击的方式对沈阳地铁网络的7个不重复站点进行攻击，并通过遭受攻击后的网络子链数目与网络效率来对比蓄意攻击与随机攻击的攻击效率。

2.1.2 子链

通过蓄意攻击与随机攻击两种方式，可得到每次攻击后网络的子链数目和最大连通子图LCC与攻击次数的关系如表2和表3所示，并绘制曲线图如图2所示。

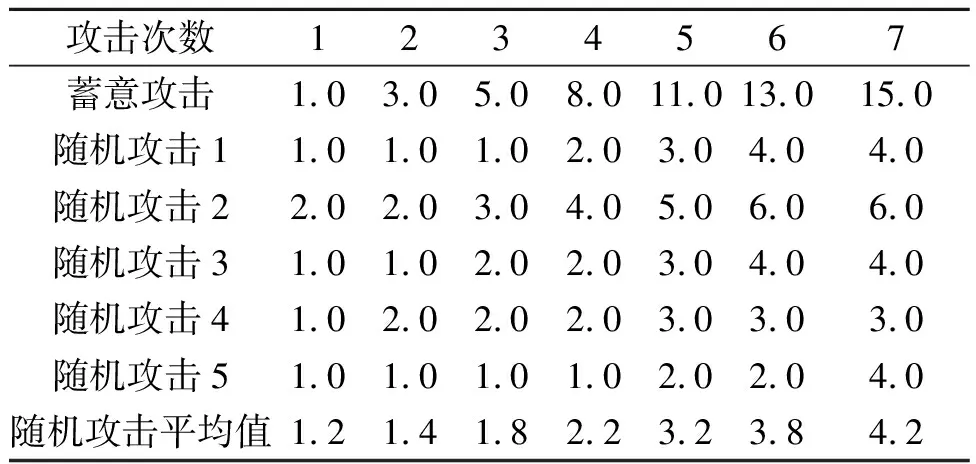
表2 子链数目与攻击次数

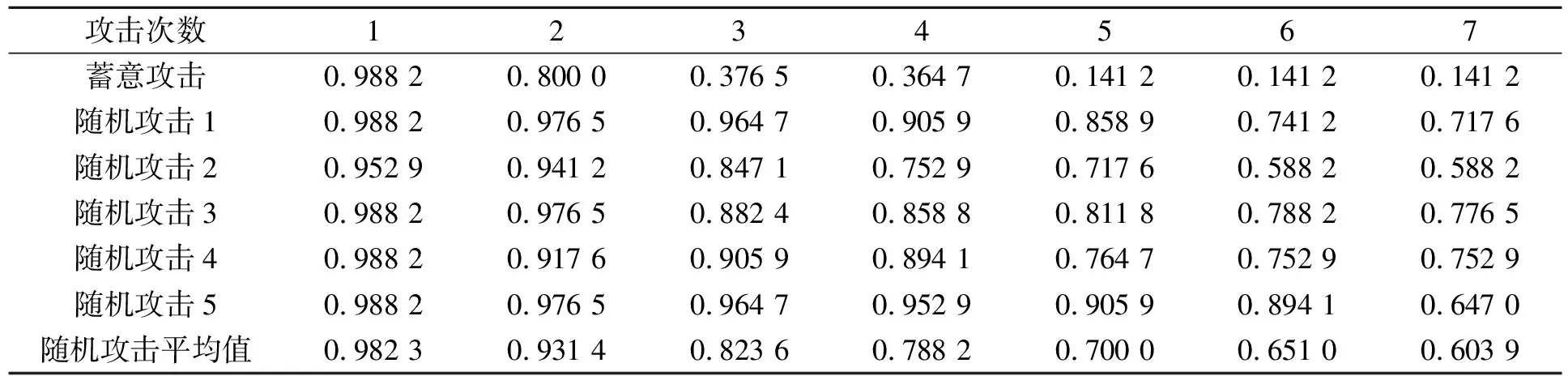
表3 最大连通子图LCC与攻击次数

图2 子链数和最大连通子图占比与攻击次数关系图

由图2(a)可知，在第二次攻击结束后，蓄意攻击后产生的子链数目已超过同期随机攻击后产生的子链数目，随着攻击次数的增加，子链数目大幅领先同期随机攻击后的子链数目。当攻击结束后，蓄意攻击产生的子链数目为随机攻击后产生的子链数目的2.5～5倍，随机攻击产生的子链数目为平均值的3.6倍；图2(b)中第二次攻击结束后，蓄意攻击后最大连通子图LCC的数目已明显低于同期随机攻击后网络产生的最大连通子图数目。当攻击结束后，随机攻击后的最大连通子图占比数为蓄意攻击后产生的最大连通子图占比数的4.2～5.4倍，随机攻击后产生的最大连通子图LCC的平均值为蓄意攻击后网络最大连通子图LCC的4.3倍。对比随机攻击的结果，轨道网络在遭遇换乘站点的蓄意攻击后，会成为产生网络连通子图半径更小、网络内连通性更差、网络结构更为零碎的轨道交通网络。

2.1.3 网络效率

通过蓄意攻击与随机攻击两种方式，可以得到每次攻击后网络的网络效率与攻击次数的关系，如表4所示，并绘制折线图，如图3所示。

表4 网络效率与攻击次数

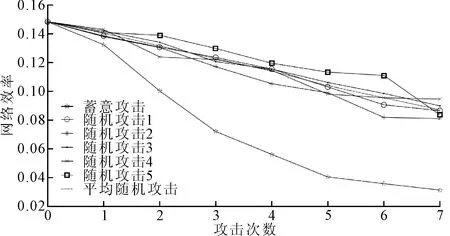
图3 网络效率与攻击次数关系图

由图3可知，第一次攻击结束后，随机攻击后剩余网络的网络效率已明显高于同期蓄意攻击后剩余网络的网络效率，并伴随着攻击次数的增加，蓄意攻击后剩余网络的网络效率的下降程度大幅领先同期的随机攻击。当攻击结束后，蓄意攻击后剩余网络的网络效率仅为随机攻击后剩余网络效率的0.32～0.38；通过计算每轮攻击后随机攻击后剩余网络的网络效率平均值，蓄意攻击后剩余网络的网络效率与随机攻击后剩余网络的网络效率的比值从0.94降至0.35。

与随机攻击相比，轨道网络在遭遇换乘站点的蓄意攻击后，网络效率更低，蓄意攻击后的网络效率下降速率更快，随着攻击的深入，蓄意攻击后剩余网络的网络效率远低于同期随机攻击后的剩余网络的网络效率，信息传递效率相较于随机攻击的方式更低。

2.2 轨道交通动态分析

通过弗洛伊德算法分别求出轨道网络间各点之间的最短通行距离,再依次攻击沈阳轨道交通的85个节点，分别统计每个站点遭受攻击后不同出行距离系数d下的可达站点数目，并计算出该点失效场景下轨道交通网络所在的可达站点占比，统计数据如表5所示，并绘制出不同d值下各站点遭受攻击后可达站点比例图，如图4所示。

表5 各站点遭受蓄意攻击后阈值d下可达站点比例α

图4 不同d值下各站点遭受攻击后可达站点占比

由表5和图4可知，地铁换乘点V12(铁西广场)、V17(青年大街)、V21(傍江街)、V34(中医药大学)、V43(奥体中心)、V49(淮河街沈医二院)、V67(长青南街)的可达站点比例的数值也都是临近站点可达站点比例数值的极小值，说明换乘站点遭受攻击后，对地铁网络的可达性影响最大；站点V1-V12、V22-V33、V44-V48、V68-V72、V84-V85失效后，可达站点比例曲线重合，与距离系数d的变化无关，不会随出行距离系数d的增加而增加。而对站点分析发现，V1-V11点对应着沈阳地铁1号线换乘点V12(铁西广场)前的网络支链节点，V22对应着1号线换乘点V21(傍江街)后的网络支链节点，V23-V33对应着2号线换乘站点V34(中医药大学)前的网络支链节点，V44-V47对应着2号线换乘站点V43(奥体中心)后的网络支链节点，V48对应着9号线换乘点V49(淮河街沈医二院)前的网络支链节点，V68对应着9号线换乘点V67(长青南街)后的网络支链节点，V69-V72对应着10号线换乘点V49(淮河街沈医二院)前一个网络支链节点，V84-V85对应着10号线换乘点V67(长青南街)后的网络支链节点。

轨道交通网络支链上的节点失效后，交通网络的可达性与出行距离系数d的阈值无关，不会随出行距离系数d的变化而变化。同时，伴随着出行距离系数d的增加，站点失效后的可达站点比例有增加的趋势：①当距离系数d=1.05时各站点的可达站点曲线与d=1.00时曲线重合率极高，说明当距离系数d由1.00增加至1.05时，各站点遭受攻击后可达站点占比未发生明显变化；②当距离系数由1.05增加至1.25时，各主链站点上的站点失效后的可达占比快速提升；③当距离系数由1.25增加至1.50时，各主链站点上的站点失效后的可达占比增幅减缓，增加速率下降明显。

通过式(10)、式(11)计算出不同出行距离系数d下轨道网络可达站点平均占比α、可达人数平均占比β，并绘制曲线，如图5所示。

图5 距离系数d与可达站点平均占比、可达人数平均占比图

由图5可知，由于可达人数占比β通过可达站点占比α与不同站点的出行人数计算得出，可达站点平均占比α曲线与可达人数平均占比β曲线的变化趋势相同，但各站点人数不同，所以曲线不重合，可达人数占比与可达站点占比总体均呈现伴随距离系数d增加而增加的现象。

由图5可知，当距离系数d由1.00增加至1.05时，站点平均可达性数值增长率为0.04%；距离系数d在1.05～1.25区间时，站点平均可达性数值增长率陡增为0.83%～1.15%；距离系数d在1.25～1.5时，站点平均可达性数值增长率陡降至0.20%～0.49%。

分析可得：①当距离系数d由1增加至1.05时，各站点遭受攻击后可达站点占比未发生明显变化；②距离系数由1.05增加至1.25的过程中，各主链站点上的站点失效后的可达占比快速提升；③距离系数由1.25增加至1.5的过程中，各主链站点上的站点失效后的可达占比增幅减缓，增加速率下降明显的现象。

在实际场景中，当站点出现故障后，交通网络主链在乘客内心对距离增加极度敏感时，人们的出行意愿无法得到有效提升，实际救援中的疏散效率无法得到有效提升；在乘客内心对距离增加敏感度超过1.05的阈值后，随着对距离系数d敏感性降低，人们的出行意愿会出现快速提升，从而大大提升疏散效率；超过1.25的阈值后，人们对于距离系数d的敏感性继续降低，对出行意愿的提升作用便不再明显。

3 结论与建议

(1)根据轨道交通网络的静态网络脆弱性分析，发现轨道交通的线路换乘站点为整个轨道交通网络脆弱性较弱的站点。当轨道交通网络的换乘点遭受蓄意攻击后，整个交通网络会破裂成子链节点个数更少、网络子链个数较多、网络效率更低的子链群体。鉴于换乘车站具有很高的脆弱性，所以在日常管理中应该重点防护，防止地铁网络在换乘站点遭受攻击后，地铁网络碎片化。

(2)从客流视角下分析网络的动态脆弱性，轨道网络中换乘点的站点/人数可达站点比例的数值均为临近站点可达站点比例数值函数中的的极小值，说明当换乘点遭受攻击后，在相同距离系数d阈值下，乘客仍能到达目的地的站点与人数都是相邻站点遭受攻击中最少的，网络脆弱性影响程度更高。所以当轨道交通网络遭遇攻击后，政策决定者应优先考虑对换乘节点站点进行修复，并主动为疏散换乘站点的受灾群众提供更多的交通疏散资源。

(3)轨道交通网络支链上的节点失效后，交通网络的可达性与出行距离系数d的阈值无关，不随阈值的变化而变化，反映为支链上的乘客的出行意愿与到轨道交通主链距离增加的阈值变化无关。而交通网络主链的乘客在受灾后：①距离系数d从1.00增加至1.05时，乘客内心对距离增加极为敏感，受困人员的实际出行意愿无法得到有效提升；②距离系数d从1.05增加至1.25时，乘客内心对距离敏感性降低，受困人员出行意愿提升明显；③当距离系数d超过1.25的阈值时，乘客内心对距离敏感性进一步降低，但站点/人数各站点受损后的可达性与平均可达性曲线增加缓慢，说明在有效增援距离超过一定范围后，乘客出行意愿提升不再明显。

(4)当轨道交通网络破碎后，可以对主链与支链乘客进行分类疏散。对于主链乘客，应选取不超过原定距离1.25倍距离的疏散目的地，可在有限的救助资源的情况下得到最好的疏散效果；对于支链的乘客，应优先考虑乘客疏散至轨道交通站外，更换交通方式，以获得更好的疏散效率。

笔者通过对轨道交通网络的动静态分析，从乘客可达性的视角，梳理复杂网络脆弱性问题，通过随机攻击与蓄意攻击的脆弱性对比，确认网络静态脆弱性较弱的网络节点；同时，通过引入出行距离系数d，通过数据仿真确认不同的参数d取值，对各站点与出行人数的可达性的影响。能为实际轨道交通事故疏散提供现实的决策帮助。后续将进一步考虑出行者的年龄构成与多种交通方式的耦合网络对出行意愿的影响。