L2空间中一个不等式的最优常数和取等条件问题

赖宝锋,陈明玉

(泉州师范学院 数学与计算机科学学院，福建 泉州 362000)

众所周知，柯西不等式是分析学中最基础和最重要的不等式之一，其离散形式[1]为：

(1)

其中：ai,bi都是实数，i=1,2,…,n，n为正整数(包括n=∞).不等式(1)取等号当且仅当存在实数λ，使得a=λb，或b=λa，其中：a=(a1,a2,…,an),b=(b1,b2,…,bn).

柯西不等式还有如下广泛运用的积分形式[1],即：

(2)

其中：f(x),g(x)∈L2(Ω).不等式(2)取等号当且仅当存在实数λ，使得f(x)=λg(x),a.e.x∈Ω,或g(x)=λf(x),a.e.x∈Ω.

不等式(1)和(2)的证明可见文[1-4].不等式(1)和(2)可视为一般的内积空间中关于内积的柯西-布涅科夫斯基不等式的特例，见文[5-7].柯西不等式有许多的加强与推广，见文[8-10]等.

现在，来研究一类与柯西不等式有关的问题.先引入如下例子：

对任意函数f(x)∈L2[0,π]，由柯西不等式，有

(3)

(4)

因此，

(5)

不等式(5)取等号当且仅当不等式(3)和(4)都取等号.由柯西不等式取等号的条件知道，这又等价于存在实数λ,μ，使得f(x)=λcosx,a.e.x∈[0,π],且f(x)=μsinx,a.e.x∈[0,π].

但cosx,sinx在L2[0,μ]中是线性无关的，故这又等价于：f(x)=0,a.e.x∈[0,π].

由此，并不能断言π就是不等式(5)中的最优常数.

类似地，由柯西不等式，有

(6)

(7)

因此，

(8)

不等式(8)取得等号当且仅当不等式(6)和(7)都取得等号.由柯西不等式取等号的条件知道，这又等价于存在实数λ,μ，使得：f(x)=λ,a.e.x∈[0,1]且f(x)=μx4,a.e.x∈[0,1].

不等式(5)和(8)是对前面的不等式经过运算得到的，所带的估计常数一般难以保证是最优的.美国数学月刊2022年4月刊也提出了如下类似的问题12318[11].

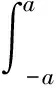
求sup{A2(f)+B2(f):f∈Sa}和sup{A2(f)+B2(f)+C2(f):f∈Sa}.类似的例子还有很多，需要对这类问题的解决建立一个统一的法则.

1 主要引理

则L2(U)就成为一个无穷维的欧氏空间.在L2(U)中，称f(x)=g(x)，如果f(x)=g(x),a.e.x∈U.

欧氏空间中，有如下的正交分解定理.

引理1[7]设V为欧氏空间，W是V的有限维子空间，则W存在唯一的正交补空间W⊥，使得

V=W⨁W⊥.

引入Rayleigh商及相关结论.

(i)R(x)的最大值和最小值分别为：

其中：λmax(A)和λmin(A)分别为A的最大和最小特征值.

(ii)当且仅当x为λmax(A)所对应的特征向量时，R(x)取得最大值；当且仅当x为λmin(A)所对应的特征向量时，R(x)取得最小值.

2 结论与证明

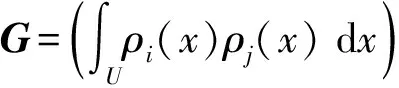
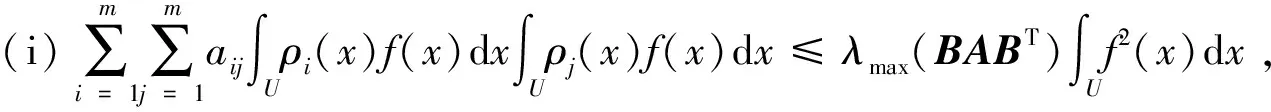
f(x)=(ρ1(x),ρ2(x),…,ρm(x))B-1y,

不等式取得等号，其中：y为BABT的最大特征值所对应的特征向量.

(ii)如果λmin(BABT)>0，则

且当且仅当f(x)∈W⊥，不等式取得等号.

(iii)如果λmin(BABT)=0，则

且当且仅当f(x)=(ρ1(x),ρ2(x),…,ρm(x))B-1y+g(x),不等式取得等号，其中：BABTy=0，g(x)∈W⊥.

(iv)如果λmin(BABT)<0，则

且当且仅当f(x)=(ρ1(x),ρ2(x),…,ρm(x))B-1y,不等式取得等号，其中：y为BABT的最小特征值所对应的特征向量.

证明W=L(ρ1(x),ρ2(x),…,ρm(x))，则W为L2(U)中的m维线性子空间.由引理1，W存在唯一的正交补空间W⊥，使得L2(U)=W⨁W⊥.

任取0≠f(x)∈L2(U)，定义泛函

作f(x)的正交分解

其中：c1,c2,…,cm∈R,g(x)∈W⊥.于是，

其中：

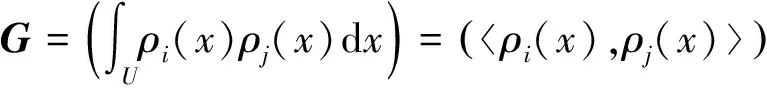
又由于

故

G为m阶实对称正定矩阵，故存在m阶实可逆矩阵B，使得G=BTB，故

由引理2，

λmin(BABT)yTy≤yTBABTy≤λmax(BABT)yTy,

故

(9)

(10)

当且仅当BABTy=λmax(BABT)y时，不等式(9)取得等号.当且仅当BABTy=λmin(BABT)y时，不等式(10)取得等号.

(i)A不是半负定的，故其合同矩阵BABT也不是半负定的，故λmax(BABT)>0.因此，

(11)

联合不等式(9)和(11)，得到

J(f)≤λmax(BABT).

(12)

不等式(12)取等号当且仅当不等式(9)和(11)都取等号，这又等价于y为BABT的最大特征值所对应的特征向量，且g(x)=0.因此，

(13)

且当且仅当

f(x)=(ρ1(x),ρ2(x),…,ρm(x))B-1y,

不等式(13)取得等号，其中：y为BABT的最大特征值所对应的特征向量.故(i)成立.

(ii)如果λmin(BABT)>0，则

(14)

不等式(14)取得等号当且仅当y=0.

联合不等式(10)和(14)，得

J(f)≥0,

(15)

且不等式(15)取得等号当且仅当不等式(10)和(14)都取得等号，这又当且仅当y=0.因此，

(16)

且不等式(16)取得等号当且仅当f(x)∈W⊥.故(ii)成立.

(iii)如果λmin(BABT)=0，由不等式(10)，

(17)

且不等式(17)取得等号当且仅当BABTy=0.因此，

(18)

且不等式(18)取得等号当且仅当

f(x)=(ρ1(x),ρ2(x),…,ρm(x))B-1y+g(x).

其中：BABTy=0，g(x)∈W⊥.故(iii)成立.

(iv)如果λmin(BABT)<0，则

(19)

联合式(10)和(19)，可以得到

J(f)≥λmin(BABT).

(20)

不等式(20)取得等号当且仅当不等式(10)和(19)都取得等号，当且仅当y为BABT的最小特征值对应的特征向量，且g(x)=0.因此，

(21)

且不等式(21)取得等号当且仅当f(x)=(ρ1(x),ρ2(x),…,ρm(x))B-1y.其中：y为BABT的最小特征值所对应的特征向量.故(iv)成立.

综上所述，定理1成立.

3 数值算例

cosx,sinx在L2[0,π]中是线性无关的，其Gram矩阵为

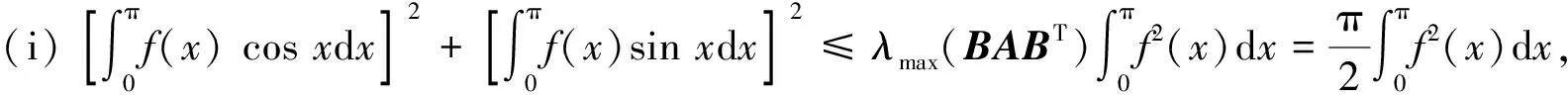
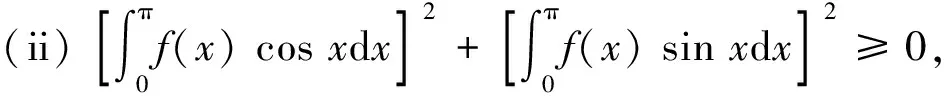
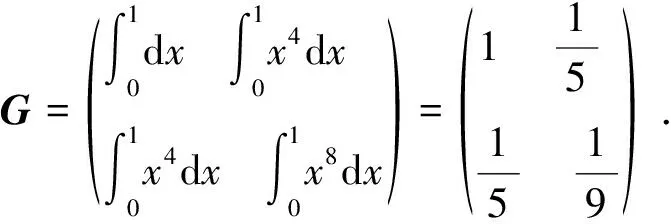
L2[-a,a]中线性无关的函数1,x的Gram矩阵为

故

L2[-a,a]中线性无关的函数1,x,x2的Gram矩阵为

因此，