犁刀式混合机飞刀轴结构设计及临界转速计算*

邹俊伟

(湖南探索机械科技有限公司，湖南 株洲 412000)

0 引 言

犁刀式混合机作为物料颗粒混合工序工业生产中的关键设备，在饲料工业、食品、制药、化工、新能源锂电材料、工程塑料等领域具有非常广泛的应用前景[1-4]。

根据犁刀式混合机工作原理，飞刀轴在驱动电机带动下高速旋转(3 000 r/min 左右)，可以起到剪碎物料颗粒中的块状物料并强烈扩散物料，加强物料颗粒的混合等作用，其一般安装在腔体上并与腔体水平面成一定的角度[5]。 飞刀轴的可靠性直接关系到混合机的可靠性及混合效率，而飞刀轴的可靠性取决于飞刀轴的结构设计及临界转速确定(横向振动问题)，所以解决上述两个问题是保证飞刀轴可靠性的前提和关键。

针对飞刀轴的结构设计及临界转速计算问题，首先建立飞刀轴受力分析模型，通过飞刀轴受力分析，利用极限计算法确定飞刀轴的最小轴径，再通过有限元法计算出飞刀轴的临界转速并验证计算结果的准确性，最后根据有限元计算结果反推出飞刀轴轴承支撑距离与轴总长之比μ≈0.3 时的支座型式系数λ1，计算方法及结果可为犁刀式混合机飞刀轴的设计提供参考和依据。

1 飞刀轴结构设计

飞刀轴工作状况为高速低载，主要承受剪碎块状物料颗粒时块状物料颗粒施加的阻反力矩TF及物料颗粒施加的摩擦阻反力矩Tf，摩擦力矩Tf由飞刀端面所受摩擦力力矩Tf1和侧面所受摩擦力矩Tf2合成:

上述力的作用使飞刀轴承受扭矩作用，得出飞刀轴受力分析图见图1。

图1 飞刀轴受力分析

根据图1，飞刀所受物料颗粒的重力由两部分组成，一部分为飞刀端面方向物料颗粒重力m1g，另一部分仅为飞刀侧面方向物料颗粒重力m2g。 设飞刀扫略区域为l(即最大飞刀直径在水平面投影长度)，最低层飞刀至腔体内壁高度为h＝1.2 m，则飞刀扫略区域的物料颗粒质量为M1，计算公式:

易知:

按极限法计算取:

鉴于物料颗粒混合时其运动轨迹的复杂性，将飞刀所受摩擦力按保守简化计算，即将离散的物料颗粒视为连续的整体。

飞刀端面上所受物料颗粒正压力:

则，飞刀端面所受最大摩擦力力矩:

式中:rmax1为最大摩擦半径，取0.09 m；f1为物料颗粒与飞刀摩擦系数，取0.6；θ为飞刀轴安装角度，取20°；g 为重力加速度，取10 m/s2。

创立于1945年的德国雄克公司 (SCHUNK GmbH & Co. KG) 是全球知名的抓取系统与夹持技术供应商。共有超过2 800名员工、9个工厂、位于50多个国家的33家子公司和代理合作伙伴，共同维护并拓展全球市场。雄克可提供11 000种标准部件，包括 2 550款标准机械手；由4 000多种自动化模块组成的完整抓取系统。雄克服务的目标行业包括机械工程、机器人、自动化装配及搬运以及所有知名的汽车生产商及零部件供应商。

飞刀侧面物料颗粒对腔体壁的正压力:

则，飞刀侧面所受摩擦力力矩为:

式中:rmax2为最大摩擦力臂，取0.09 m；f2为物料颗粒与腔体壁摩擦系数，取0.6；θ为飞刀轴安装角度，取20°。

联立式(1)、(6)、(8)并代入数据得:

联立式(4)、(9)进一步可得:

联立式(2)、(10)得:

设飞刀剪碎块状物料颗粒时剪碎力为F，则:

式中:h为块状物料颗粒高度，取10 mm；b为犁刀与块状物料颗粒接触宽度，取4 mm；σ为块状物料颗粒剪切强度，取1.3 MPa；f为物料颗粒与腔体内壁摩擦系数，取0.6。

数据代入式(12)得:

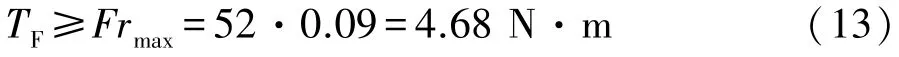
式中:rmax为最大飞刀半径，取0.09 m。

根据式(11)、(13)计算飞刀承受的阻反力矩:

按扭转强度计算飞刀轴最小轴径[6-7]:

式中:T为轴所传递的扭矩，24 000 N·mm；τp为许用扭转切应力，取30 MPa。

代入得:

2 飞刀轴临界转速计算

2.1 理论计算飞刀轴一阶临界转速

为避免飞刀轴工作时发生弯曲共振(横向振动)，飞刀轴作为刚性轴，其最高转速应低于一阶临界转速，即飞刀轴最高转速应满足如下条件[8]:

式中:ncr1为飞刀轴一阶临界转速，r/min。

因飞刀轴为双绞支支撑方式并计轴自重(飞刀轴、飞刀材质为SUS304 不锈钢)，用邓柯莱(Dunkerley)简化公式求其一阶临界转速[7]:

式中:λ1为一阶临界转速时支座型式系数；W0为轴所受重力，11.48 N；L为轴全长，285 mm；l为支撑间距离，84.7 mm；Gj为外伸端第j个圆盘(飞刀)所受重力，N；cj为外伸端第j个圆盘(飞刀)至支撑间的距离，mm。 参数见表1；dv为轴的当量直径，mm。

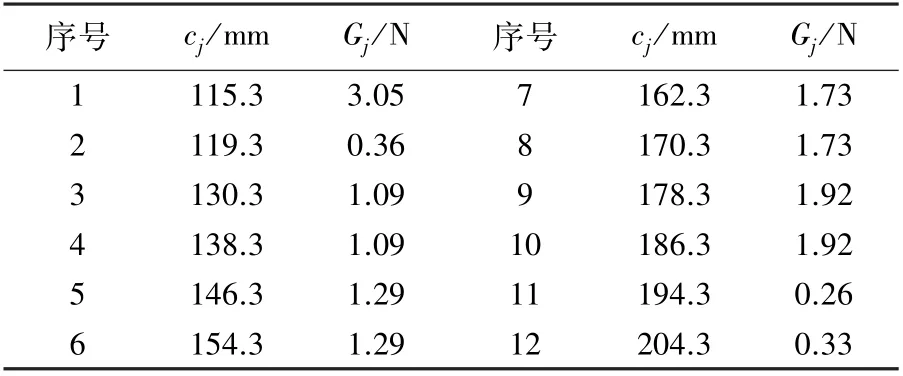
表1 等效圆盘(飞刀)支撑参数

飞刀轴的当量直径按下式计算[7]:

式中:di为第i段轴直径，mm；Δli为第i段轴长度，mm。 参数见表2；ξ为经验修正系数，取1.094。

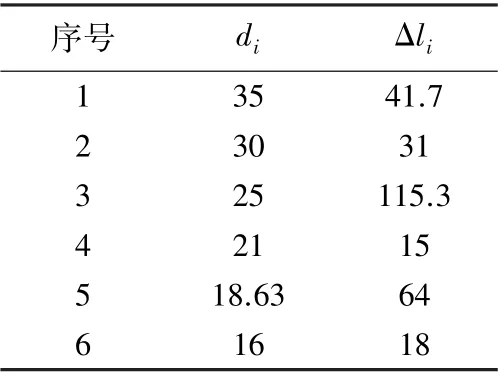
表2 飞刀轴轴段参数 /mm

因飞刀轴支撑间距离μL与轴总长L之比μ＝0.3，见图2[7]，通过查阅机械设计手册或相关文献，无对应的支座型式系数λ1。 为确定λ1取值，利用有限元计算软件计算出飞刀轴一阶临界转速，再取可选的支座型式系数λ1，结合理论计算验证有限元计算的准确性，最后根据有限元计算出的飞刀轴一阶临界转速结果反推出μ＝0.3 时的一阶临界转速对应的支座型式系数λ1。

图2 轴支撑距离与轴总长度之比

2.2 有限元法计算飞刀轴一阶临界转速

对飞刀轴进行频率分析，在有限元计算软件中导入飞刀轴实际三维模型并划分网格，飞刀轴有限元计算模型见图3。

图3 飞刀轴有限元模型

飞刀轴的约束为双支点轴承约束。 因飞刀轴承受载荷类型为力矩，而力矩载荷对结构固有频率影响甚微，在此忽略，所以飞刀轴频率分析时不施加力矩载荷。 频率分析结果见图4。

图4 飞刀轴频率有限元计算

由图4 可知，飞刀轴一阶固有频率为180.54 Hz，通过进一步计算可得到飞刀轴的一阶临界转速约为10 832 r/min。

3 飞刀轴临界转速理论与有限元法计算比较

为反推出μ＝0.3 时飞刀轴一阶临界转速理论计算时对应的支座型式系数λ1，并验证有限元计算的准确性，分别取λ1＝0.5、0.55、0.6，其余参数保持不变，再分别根据式(18)、(19)对比理论和有限元法计算结果。 计算结果见表3 所列。

表3 不同λ1 时一阶临界转速计算结果及误差

根据表3，理论计算与有限元法计算飞刀轴一阶临界转速最大误差为4%，进一步可以确认理论计算及有限元法计算飞刀轴一阶临界转速的准确性，从而可根据图4 计算结果及式(18)、(19)反推出μ＝0.3时飞刀轴一阶临界转速理论计算时对应的支座型式系数λ1。 按最大误差4%计算，取比有限法计算结果小的值，得λ1＝4.49。

联立式(17) ～(19)得出飞刀轴一阶临界转速ncr1min为:

取飞刀轴最小一阶临界转速ncr1min为飞刀轴一阶临界转速。 进一步，根据式(17)，可得飞刀轴转速ωmax最大值为:

4 结 语

针对飞刀轴的结构设计及临界转速计算问题，首

先建立飞刀轴受力分析模型，通过飞刀轴受力分析，利用极限计算法得到飞刀轴最小轴径取16 mm 可满足强度要求，再通过有限元法计算得到飞刀轴的临界转速为7 798 r/min，并结合理论计算方法验证了计算结果的准确性，最后根据有限元计算结果反推出飞刀轴轴承支撑距离与轴总长之比μ≈0.3 时的支座型式系数λ1＝4.49。 计算方法及结果可为犁刀式混合机飞刀轴的设计提供参考和依据。