基于PSO 优化小波变换的测井信号去噪研究*

魏振华，胥越峰，刘志锋，舒志浩

(1.核技术应用教育部工程研究中心，江西 南昌 330013；2.东华理工大学 信息工程学院，江西 南昌 330013；3.江西省放射性地学大数据技术工程实验室，江西 南昌 330013)

0 引言

在测井信号的采集、处理、转发过程中，由于环境、仪器、人为等因素的干扰测井信号中总会存在噪声，如果不经处理直接使用这些带噪信号会对矿产勘探产生误差，更有严重者甚至会造成重大的经济损失。因此，在信号处理的过程中去除测井信号的噪声就显示出了必要性。测井信号去噪有很多方法，小波变换突破了以傅里叶为代表的传统方法的显著缺陷，在时频域上都有着亮眼的表现，是去噪方法的主要技术之一。

主流的研究表明小波变换的参数设置会直接影响最后的滤波去噪效果，如李维松等统合硬、软以及Garrote 阈值去噪的优点，构造出一个新的改进阈值函数，在突变性及平滑性信号方面取得了更优的降噪成果[1]；朱荣亮等为更好地滤除噪声，提出一种新阈值函数，通过仿真确定最佳小波函数类型和分解层数[2]；谢政宇等根据均方根误差和平滑度的变化特性构建了一种复合评价指标，通过评价指标来优选小波参数[3]。但是在对测井信号的处理中，因测井数据的庞大与多样性，单独改进阈值函数等对不同地区、不同井、不同井次、不同测井曲线的去噪效果不够好，所以在参考了解文献[4]-[6]中体现出粒子群算法寻找最优点的优势以及测井信号处理的实际需求后，采取群智能算法中的粒子群算法(Particle Swarm Optimization，PSO)来获取不同目标下的最佳小波变换参数，并对粒子群算法做一定的优化。

粒子群算法的优化的侧重点在于兼顾粒子在迭代前期的全局搜索能力与后期的局部搜索能力。因此，在该思想的指导下，大量研究学者提出了实时变化的惯性权重策略。目前来说，有线性、非线性、自适应几种策略可供选择。钟臻等提出了线性递减惯性权重策略的粒子群算法[7]；华勇等提出的非线性权重递减策略的改进粒子群算法[8]；除了建立起惯性权重ω 与迭代次数t 关系，邢雪提出自适应权重策略的粒子群算法[9]。

本文提出应用随机惯性权重策略改变粒子群算法权重参数，引入自然选择机制，综合考虑粒子的全局搜索与局部搜索能力，在收敛速度快的同时又不至于过早收敛，还保证了种群的多样性，适用于在大量测井信号小波阈值去噪参数组合中获得最佳小波变换参数，将最佳小波变换参数应用到小波去噪中，有效分离了有用信号和无用噪声。

1 小波变换去噪基本原理

去除数据相关性是小波变换具备的特征，能够隔开噪声与有用信号的系数。其中，较小的系数主要对应测井信号的噪声，而有效信息的系数幅值一般大于噪声的系数幅值，因此通过选择恰当的阈值，将低于该阈值的系数归0，用剩余的系数重构测井信号从而达到滤波的目的[10-11]。

小波变换的数学形式可以表示为：

式中，a 为伸缩因子，b 为平移因子，平移和伸缩基本小波函数φ(t)后获得小波基函数φa，b(τ)。

小波变换使用滤波器来分解测井信号，得到了相应的近似系数CA和细节系数CD。实际操作时使用MATLAB自带的方法来分解测井信号并完成后期的测井信号重构。

基于小波阈值去噪的流程图如图1 所示。

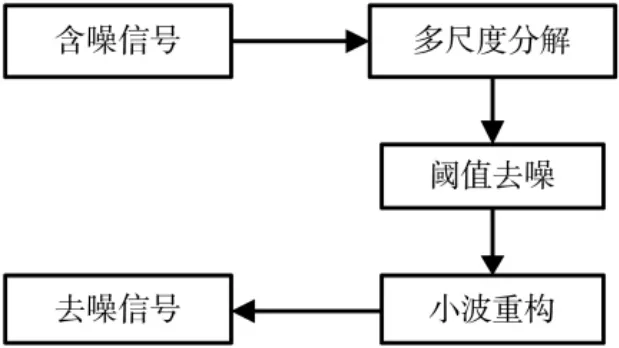
图1 小波去噪流程

小波去噪具体步骤如下：

(1)信号分解。计算信号第1 层～第L 层分解的小波系数CA+i、CD+i(i=1～L)。

(2)小波系数阈值的选取。得到1 层～L 层的阈值，对细节系数CD进行处理。阈值通常基于噪声幅度的标准偏差(σ)来定义，阈值规则根据式(2)选取[12]：

其中，f(n)是原始测井信号，φ是噪声，μ是噪声幅度，n是样本数。

(3)信号重构。根据第1～L 层的CD和第L 层的CA，实现SL的重构。

三层小波分解与重构如图2 所示。小波变换参数取值范围如表1 所示。

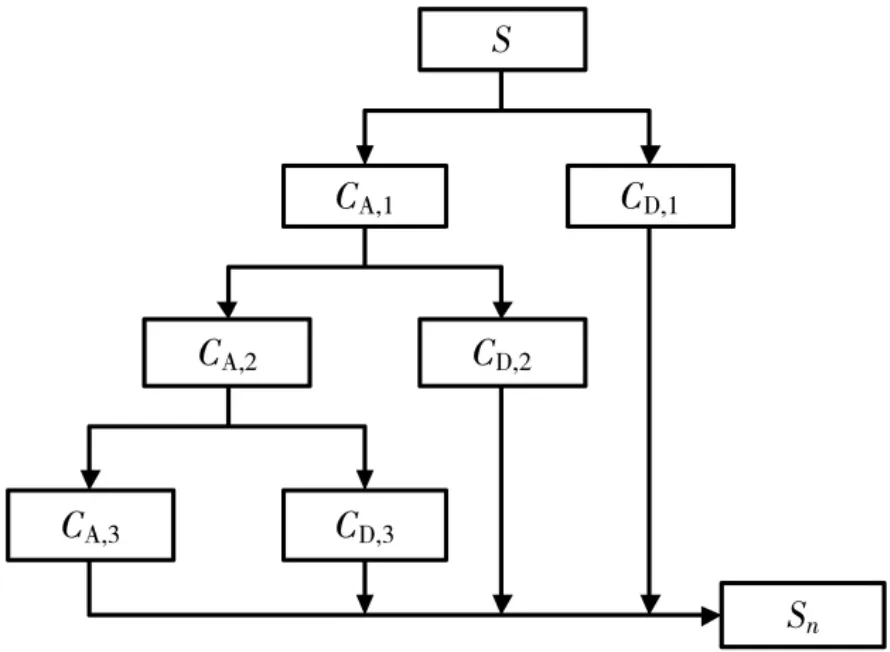
图2 三层小波分解与重构示意图

表1 小波变换参数范围表

2 粒子群算法

2.1 经典粒子群算法

粒子群算法是Eberhart 和Kennedy 于20 世纪末提出的一种生物启发式方法[13]。通过对自由生活的鸟群做数学模拟，研发出了基于群智能的粒子群优化算法。当鸟群出去觅食时，每只鸟下一次的行动都是来源于个体鸟类经验与鸟群经验的累加，每当有一只鸟更靠近了食物，所有个体鸟类都将根据鸟群经验来更改自己的飞行速度与方向，通过个体鸟类的竞争与协作，鸟群将逐渐接近食物所在的区域，最后实现全局最优解的搜索。

在这个D 维的解搜索空间，粒子所代表的每一个鸟类都将找到最终解，通过速度更新式(3)和位置更新式(4)，粒子将按照自己的运动速度及个体最优解(pbest)与群体最优解(bbest)来决定自己的移动，t 次迭代过后，全部粒子抵达了最终区域，收敛到了全局最优解。

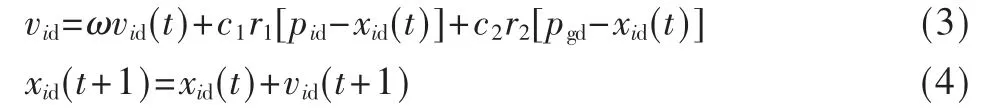
式中，ω 为粒子的惯性权重；第i 个粒子的飞行速度为vid；t 为迭代次数；xid(t+1)表达在D 维空间内第i 个粒子在t+1 次迭代中的位置；c1、c2为用来调整粒子状态的非负常数；r1、r2为(0，1)上 随机分布的随机 因子；pid为第i 个粒子的个体最优解，pgd为群体最优解。

2.2 改进PSO 算法

目前，PSO 的研究重点是算法理论分析方面、参数结构等改进方面、与其他算法融合方面、实际应用方面共四方面[14]。而本节的研究中心是对PSO 算法惯性权重进行改进，平衡整体过程中粒子的搜索能力，使粒子不至于陷入前期就停滞的局面，能在邻域内找到更多的解；又提高后期的局部搜索能力，增强搜索精度。从经典的PSO 算法公式可以看出，主要是对惯性权重、学习因子两种参数调整以作粒子群算法的改进。

目前有几大策略，分别是：线性递减惯性权重策略、非线性权重递减策略、自适应惯性权重策略。

本文综合考虑粒子的迭代前期探索与迭代后期开发能力，如果初始化的ω 值较小，其就容易陷入过早收敛的缺点，探索能力差。因此要面对初期ω 低而导致递减后无法脱离局部最好点的问题，需要将ω 的生成公式置为随机产生，所以使用随机惯性权重策略对PSO 改进，主要公式如下：

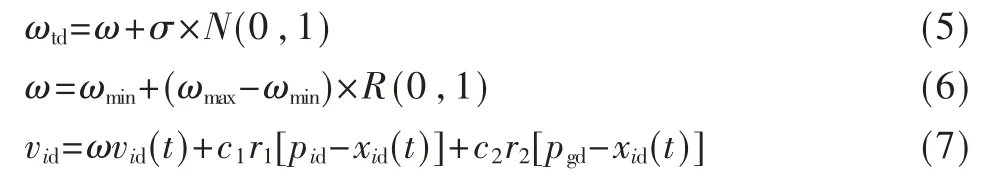
式中，N(0，1)表示为标准正态分布的随机数，R(0，1)表示0～1 之间的随机数，σ 表示标准差。

为解决种族多样性的问题，引入自然选择机制。在计算并比较好所有粒子目标函数值后进行自然选择，更新粒子速度与位置，按目标函数值高低排序并筛选更高的1/4 粒子，将排序更高的这部分粒子与排序最后的1/4 粒子交换其速度与位置信息，这样就增强了PSO 的探索能力，并改善了对开发区域的信息的使用程度，使算法脱离局部最优的能力较强，适合测井信号去噪参数选取。改进后的IPSO 算法解决了易陷入局部最好解的问题。

2.3 仿真实现

选用函数进行测试，对照辨析其他学者的算法与笔者改进算法的结果。测试函数如下所示：

实验环境：操作系统为Windows 7，电脑配置为Intel®CoreTMi5-4210U CPU@1.70 GHz，内存配置为8 GB，MATLAB版本为R2016a。

算法参数设置如表2 所示。

表2 算法参数设置表

相应的测试结果图如图3～图7 所示。

图3 基本粒子群算法

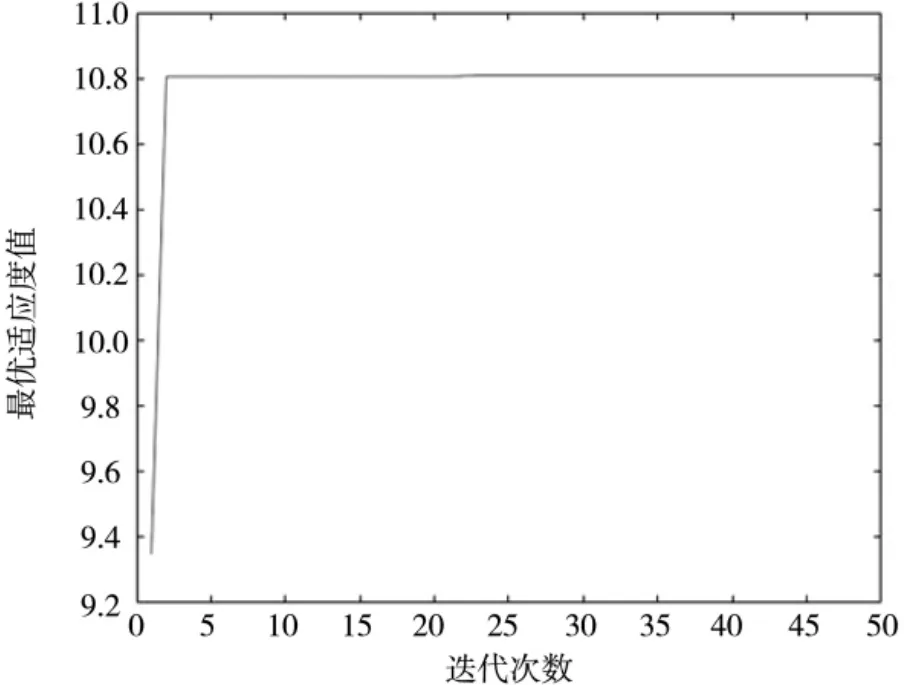
图4 线性递减惯性权重

从图3～图7 可以看出，在上述5 种方法中本文提出的改进PSO 算法效果最好，有多个局部极值，保证了种族的多样性，避免了一般PSO 算法的过早收敛问题，在小波阈值去噪的大量参数组合中保持了良好的探索能力，不至于因动量较小而陷入某个局部极值中无法脱离。正适合在本文的大量测井信号小波阈值去噪参数组合中选取最佳组合。

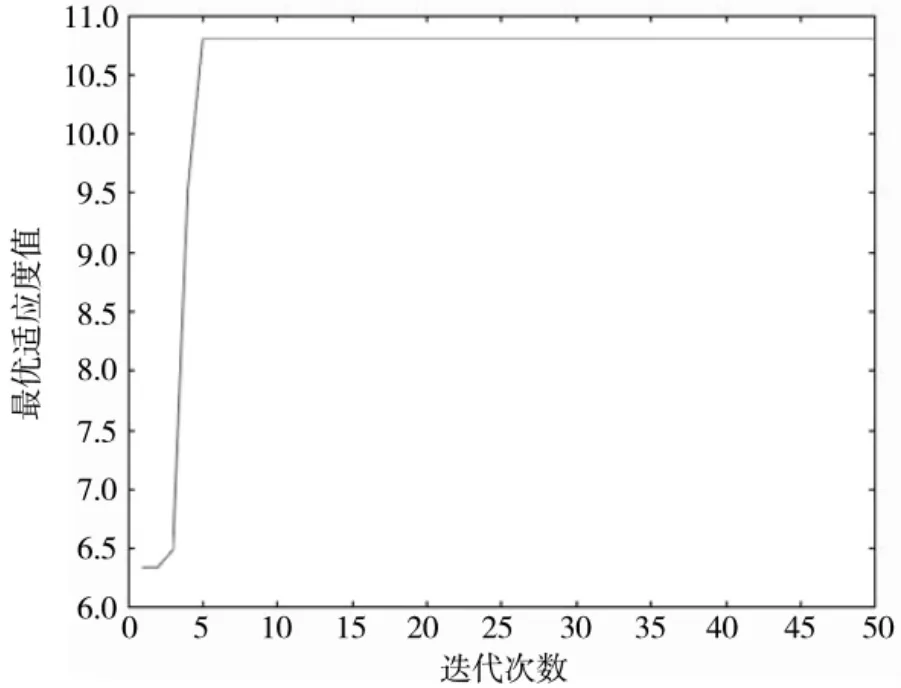
图5 非线性权重递减

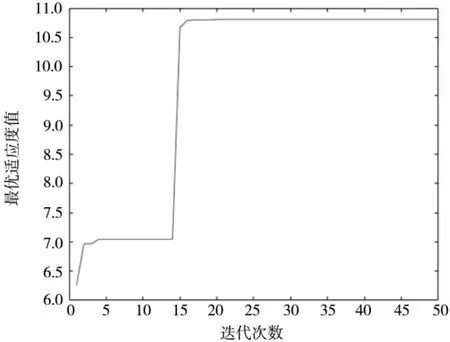
图6 自适应惯性权重

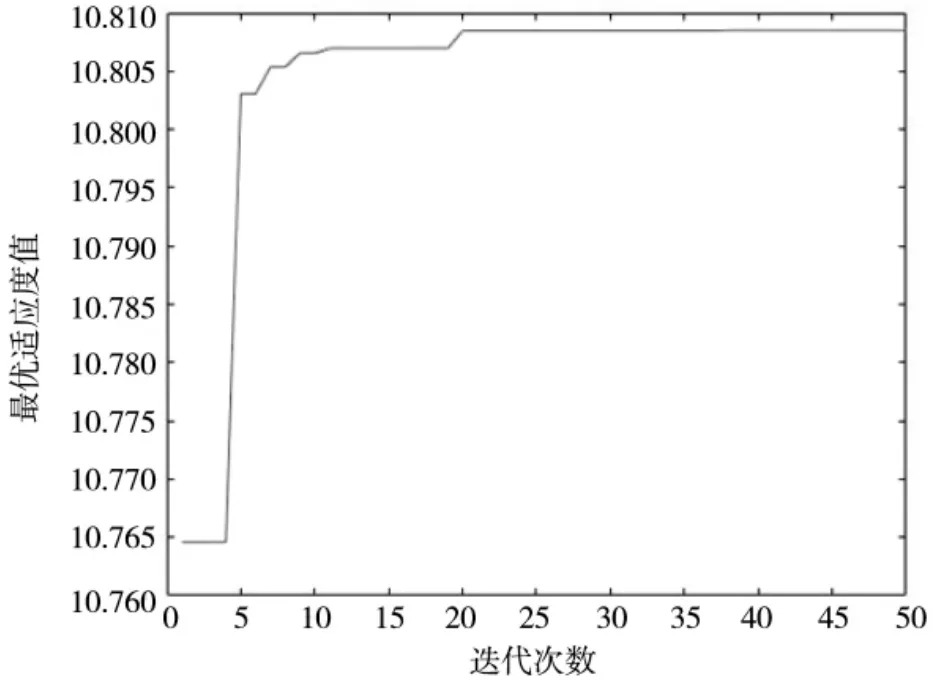
图7 IPSO(本文改进)

3 基于改进PSO 优化小波变换的测井信号去噪方法

本文研究小波变换测井信号去噪的方法，提出使用改进后的IPSO 算法来获得最佳小波变换参数以获取更适合目标测井信号的去噪效果。本文提出的方法分为以下3 个阶段：

(1)预设粒子群参数，如表3 所示，获取目前迭代次数下的ω 值。

表3 IPSO 算法初始化参数值表

(2)读取原始测井信号，增添高斯白噪声，计算测井信号的均方误差MSE。把MSE 作为适应度函数，以此寻优最佳小波阈值参数。MSE 由式(9)计算得到。照2.2 小节中提出的改进算法更新全体粒子权重、速度和位置，得到测井信号对应的最佳小波阈值参数。

(3)用获取的参数去噪，并计算去噪前后的均方根差PRD、信噪比SNR。进行如下3 步：①用获得的最佳小波参数作测井信号分解；②用获得的最佳小波参数作小波系数阈值的选取；③重构去噪后的测井信号并做去噪前后的对比。

4 实例应用、实验结果及分析

采用实际测井数据，将改进后的去噪方法应用到套管深度识别中，体现其实用性。

4.1 套管深度识别

在下放测井仪器时，与表层土、岩层、水、油等相比，套管会在测井曲线上有不同的响应，因此可以利用测井曲线识别出套管深度。而在长庆油田，井径曲线和电阻率曲线数据更容易获得且兼具明显的可用于套管深度识别的响应特征、井径曲线的扩径特征和电阻率曲线的归零特征，因此本文选用了这两条曲线。

小波分析是测井资料处理常用方法之一，与另一种常用方法傅里叶变换相比，小波分析可以探测到信号中的瞬态信息，同时也可以展示其频率成分，更适用于套管深度识别；高斯函数本身具有的特点使其可以被用来利用小波变换确定曲线的极值。

因此基于高斯小波变换和对数变换的套管深度自动识别算法结合井径曲线CAL 的扩径特征和电阻率曲线HLLD 的归零特征，对井径曲线作高斯小波变换、电阻率曲线数据作对数变换，取高斯小波变换后的第一个极大值来识别套管深度。

其基本思路如下：

(1)识别井径曲线时，选取高斯小波变换后的第一个极大值，极大值所处的尖峰即为扩径。

(2)在识别电阻率曲线时，设置一个值，如果电阻率小于该值，即认为是出现归零。

(3)根据两种特征所识别出的套管深度值的可信度来综合判断套管实际深度。

4.2 实验结果及分析

实验数据采用我国北部某知名油田的实际测井数据，实验环境：操作系统为Windows 7，电脑配置为Intel®CoreTMi5-4210U CPU@1.70 GHz，RAM 为8 GB，MATLAB版本为R2016a。系统的降噪性能通过指标信噪比SNR、均方根差PRD 来评价。SNR、PRD 计算方程如式(10)和式(11)所示：

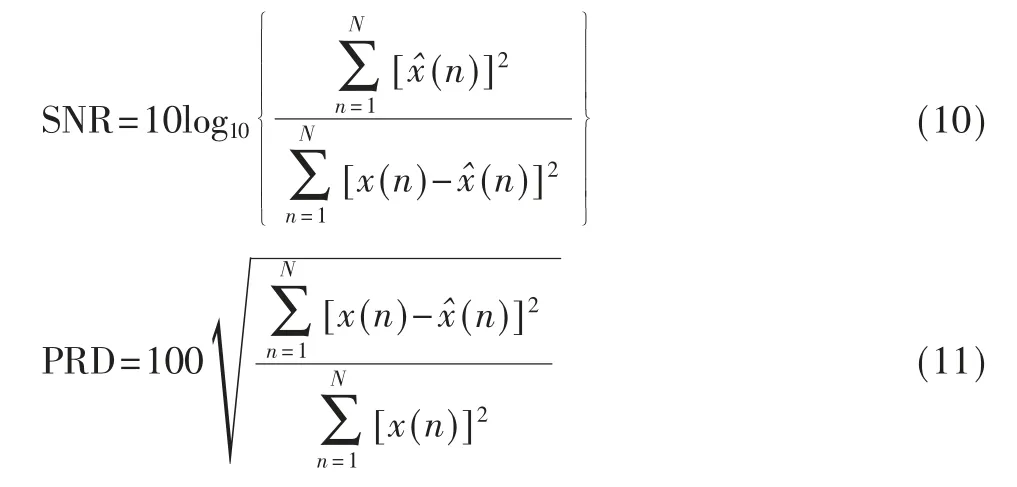
在原始测井信号中加入0～30 dB 的白噪声，用本文提出的去噪方法去噪，并对去噪前后的SNR 和PRD 作比较，得到如表4、表5 所示的实验结果。

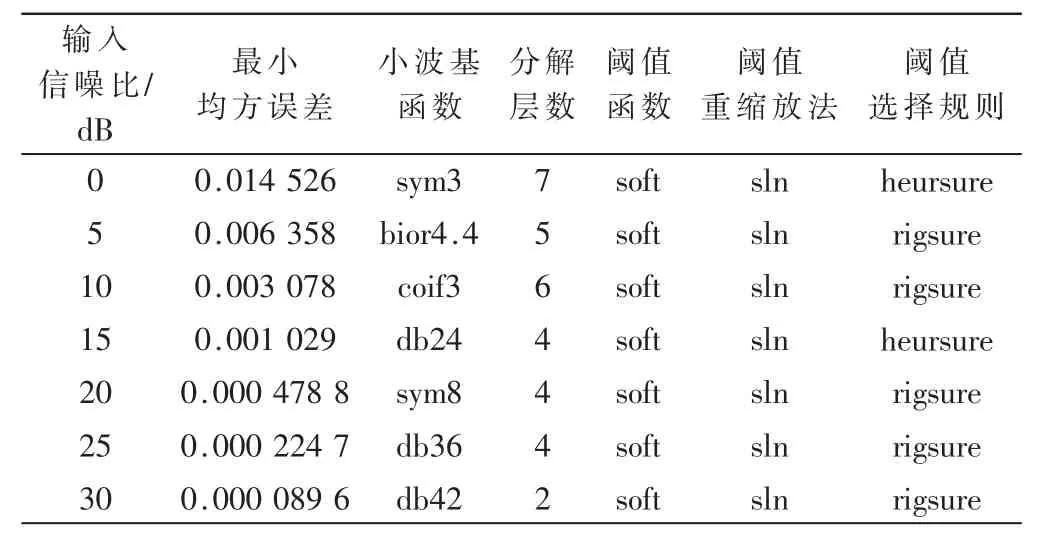
表4 IPSO 获得的最佳小波变换参数

如表4 所示，在低信噪比阶段时，小波基函数最优选择为sym、bior、coif，分解层数为5～7层，阈值函数为软阈值函数，阈值重缩放法为sln，阈值选择规则为一次heursure、两次rigsure，rigsure 更优；而在高信噪比阶段时，小波基函数为3 次db、1 次sym，分解层数为2～4层，阈值函数为软阈值函数，阈值重缩放法为sln，阈值选择规则为一次heursure、3 次rigsure，rigsure 更优。表5 给出了输入不同信噪比情况下基于PSO 优化小波变换的测井信号去噪方法的去噪性能。

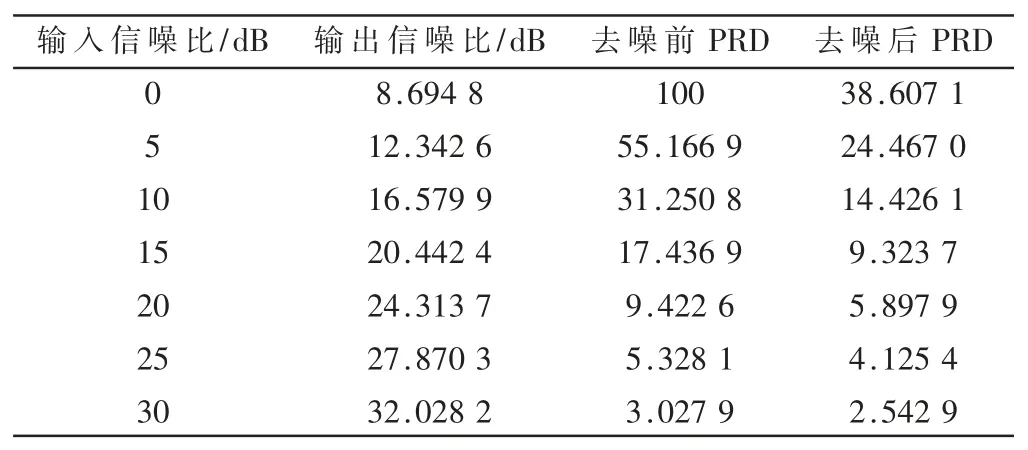
表5 输入不同信噪比对测井信号去噪性能的影响

由表4、表5 可知，去噪前后PRD 变动随输入信噪比的增加而逐渐平稳。在本组实验数据中，不同输入信噪比情况下，经基于PSO 优化小波变换的测井信号去噪方法去噪后的信号其SNR 均有较大提升，PRD 也较明显降低，证实了本文提出测井信号去噪方法的有效性。

套管深度识别最后识别出如表6 所示的11 口井的套管深度。从实际应用的结果来看，81.8%的电阻率曲线识别出的套管深度误差都在0.5 m 以内，81.8%的井径曲线识别出的套管深度没有误差，在研究区域，该识别方法行之有效。从套管深度自动识别系统与人工判断两种方法得到的套管深度的效果对比中可以明显看出，本文方法可以极大地节省测量人员的时间和精力，并且误差较小，可以满足套管识别的信息化发展，将工作人员从繁琐的机械式人工判断套管深度中解放出来，能够将更多的精力放在更重要的工作中。

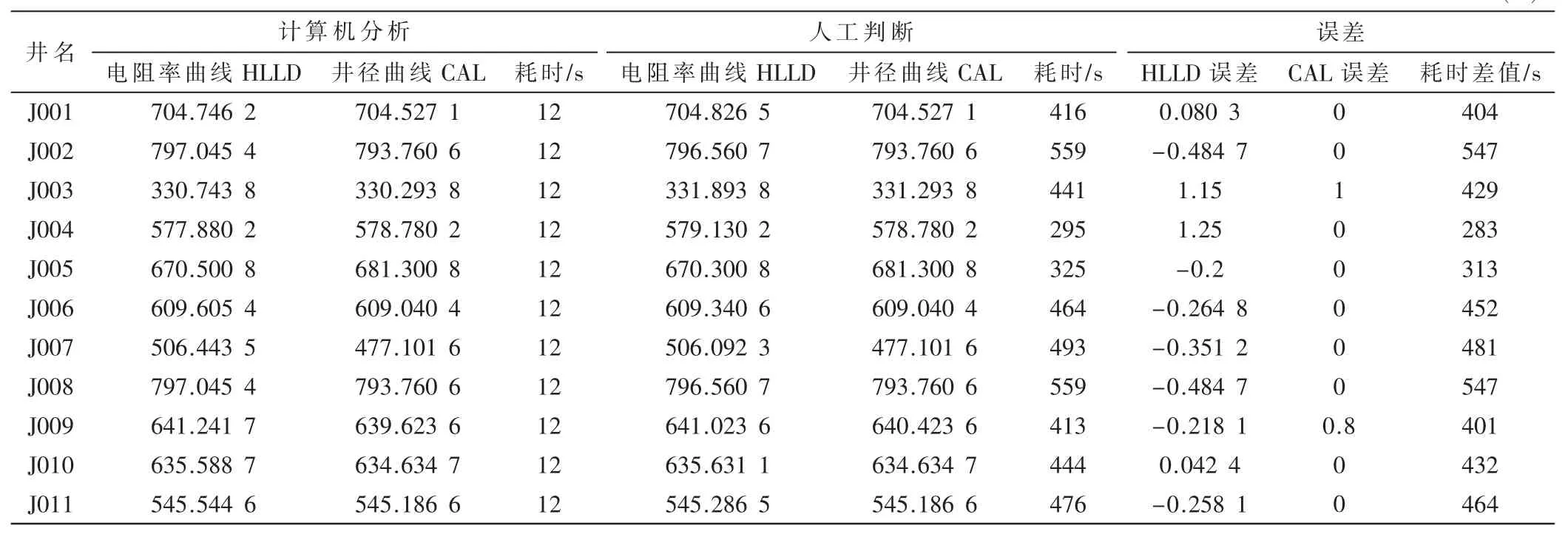
表6 实验效果对比分析 (m)

5 结论

基于小波变换的测井信号去噪方法是勘探领域研究的一个重要课题，常规的方法是用经验公式获取去噪参数，一般研究者们是在阈值函数等领域提出改进，而本文则采用粒子群算法来优化小波变换5 种参数的选取，获得对当前测井数据去噪效果最好的小波变换参数，在测井信号处理这种大数据多样性的问题中占有优势。本文使用改进的PSO 算法来获取小波变换去噪的最佳参数，并将其应用到套管深度识别中，得到更好的去噪结果，有效地提高了去噪测井信号的信噪比，更好地实现了有用信号和无用噪声的分离，为勘探领域测井数据的去噪提供一种新的方法。