考虑数字控制延时的UPS 逆变系统控制器设计*

饶刚，王国锐

(1.武汉科技大学 机械传动与制造工程湖北省重点实验室，湖北 武汉 430081；2.武汉科技大学 武汉科技大学精密制造研究院，湖北 武汉 430081)

0 引言

随着当今社会进入互联网时代，计算机普及，以及信息化产业迅速发展，对电力供电设备提出了越来越高的要求[1-3]。不间断电源(Uninterruptible Power Supply，UPS)作为一种保证计算机服务器、交换机等用电设备安全运行的电源装置，行业应用标准越来越高[4-5]。逆变器及其控制系统作为UPS 的核心部分，必须具备输出高质量电压波形的能力[6]。从技术发展趋势来看，要获得具有优越的稳态精度、快速响应以及抗干扰能力的高性能UPS，离不开优良的数字控制技术[7-9]，而逆变控制系统采用数字控制技术具有的特有问题之一是由采样、计算、PWM调制等过程产生的延时环节对控制系统的稳定性能和动态性能造成的负面影响。文献[10]、[11]采用数字控制方法来改进逆变系统的控制性能，但并未考虑数字延时带来的影响；文献[12]考虑了数字延时带来的影响，并通过控制方法来消除延时的影响，但是却增加了系统的复杂性；文献[13]分析了数字控制延时产生的原因，但并没有在考虑延时的情况下对系统控制参数进行设计。

解决逆变控制系统中的数字控制延时问题最简单方法就是在进行系统控制器设计时考虑延时的影响，保证控制系统具有良好的输出特性。为了进一步提高UPS逆变控制系统的性能，本文首先对单相UPS 逆变控制系统进行数学建模，分析了数字控制延时对系统性能的影响，引入广义Z 变换改进逆变控制系统的模型，给出了考虑延时环节的数字PID 控制器参数修正设计方法。最后在以STM32 为核心控制器的逆变器样机上进行了验证，实验结果验证了理论分析的可行性和有效性。

1 单相UPS 逆变系统数学模型

图1 为单相UPS 逆变器带无源LC 低通滤波器的等效电路模型，L 为滤波电感，RL为滤波电感的等效串联电阻，C 为滤波电容，RC为滤波电容的等效串联电阻。由于逆变电路中含有功率开关管等非线性元器件，本文采用状态空间平均法对逆变电路进行线性化分析，建立系统的数学模型。

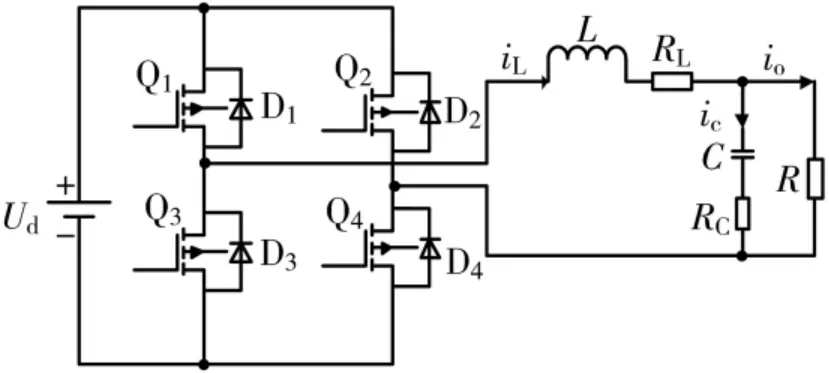
图1 单相UPS 逆变器等效电路模型

选取电感电流iL和电容电压UC作为系统的状态变量，x1=iL，x2=UC。当逆变器开关频率远大于输出滤波器的截止频率时，逆变桥可以等效成增益为KP的比例环节。根据基尔霍夫电流电压定律可列出系统的约束方程为：

式中，iL为电感电流，ic为电容电流，io为输出电流，UL为电感电压，UC为电容电压，RL是滤波电感的等效串联电阻，RC是滤波电容的等效串联电阻。

由式(1)～(3)可以推导出单相UPS 逆变系统的状态空间表达式为：

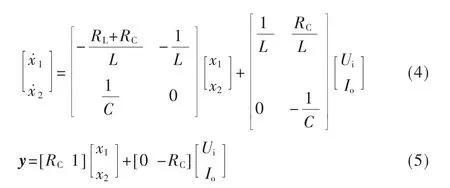
由式(4)、式(5)可推导出双输入Ui、Io同时作用时逆变系统的复频域输出响应关系式为：

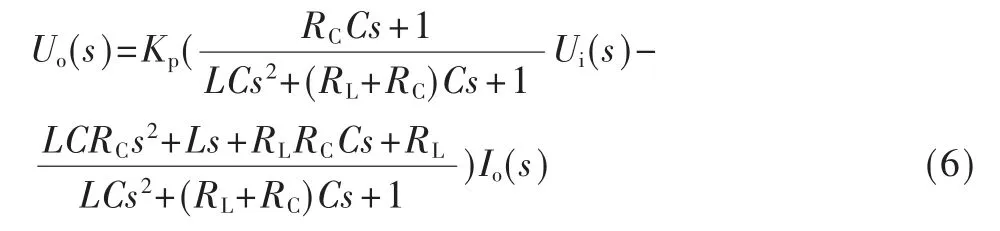
在实际电路中，电容等效串联电阻RC值很小，对系统的控制性能影响很小，一般忽略不计。则可以得到如图2 所示的单相UPS 逆变系统的状态空间模型框图。

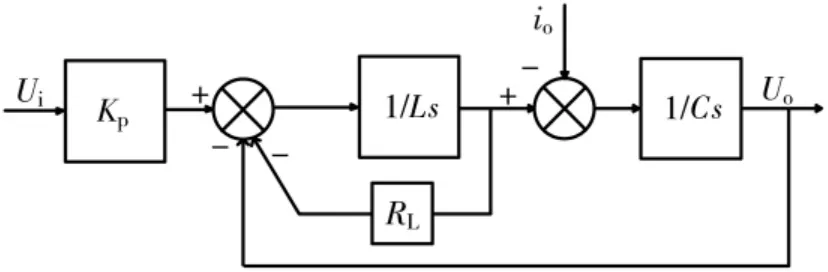
图2 单相UPS 逆变系统的状态空间模型

2 延时环节对逆变控制系统的影响

由于逆变控制系统采用电压电流双闭环控制技术，而电流内环的响应速度是电压外环的5～10倍，因此仅对电流内环进行分析,电流内环采用P 控制器，比例系数为K。

根据式(6)和图2 可得被控对象的传递函数为：

延时环节等效为一个一阶惯性环节，其传递函数为：

那么电流内环结构图如图3 所示。

图3 电流内环结构图

当不考虑延时环节时，根据式(7)和图3 可得到电流内环开环传递函数为：

如果将系统带宽定义为当闭环系统幅频特性幅值衰减到ω=0 时幅值的0.707 倍所对应的频率，根据式(9)，只要整定得到合适的PID 控制器的参数，在不考虑延时环节的理想控制系统中就可以得到无穷大的控制带宽。

若考虑延时环节时，电流内环开环传递函数为：

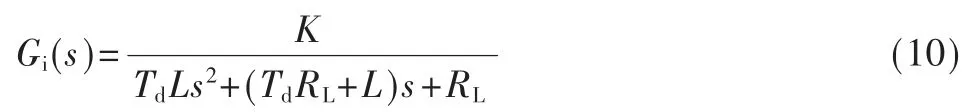
根据式(10)，不同Td值下的电流内环的闭环伯德图如图4 所示，可知，当延时减小时，内环系统的带宽明显增宽，可见若是采用传统设计方法，忽略延时环节而获得的控制器参数，会使控制系统的稳定性变差甚至出现不稳定的状况，从而影响系统的输出性能。因此在数字控制系统设计时，必须考虑控制延时的影响，对控制器参数做修正设计，以提高系统的控制性能。

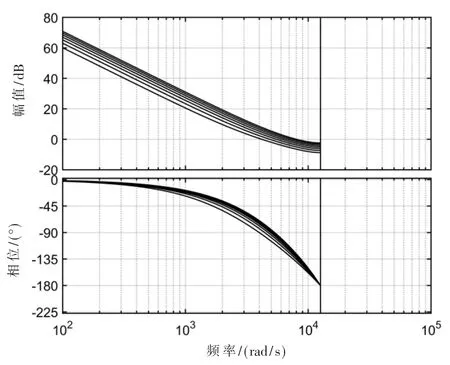
图4 不同延时下电流闭环系统伯德图

3 考虑延时的数字PID 控制器设计

忽略延时环节会导致数字控制系统性能下降，表现为稳态精度差、动态响应慢等问题，为了消除延时环节的带来的负面影响，本文引入广义Z 变换理论来描述延时环节，改进传统的控制结构模型，根据根轨迹法，修正内外环数字化PID 控制器模型参数。

3.1 电流内环控制器

图5 离散后的电流内环结构图

Z 变换仅仅是描述采样点上的信息，当系统中的延时环节是采样周期的整数倍时可以用Z 变换，而广义Z变换可以描述采样点间的信息，因此可以用来描述任意的延时环节。在逆变控制系统中，延时环节Td=mTs，不是开关周期的整数倍，则可以根据广义Z 变换理论获得内环系统考虑延时环节e-Tds后的传递函数模型。将延时Td=mTs插入到内环系统中，则可以得到改进后的开环系统的传递函数为：

由式(11)得出电流内环开环根轨迹如图6 所示。内环系统的主导极点位置由内环比例控制器增益K 唯一决定，系统的控制性能由增益K 所决定。根据根轨迹法，取系统阻尼比ξ=0.707 使内环系统具有相对稳定性和足够的快速性。由图6 可知，当阻尼比ξ=0.707时，电流内环系统的增益Ki=0.218，则可得到电流内环比例控制器参数K=29.5。

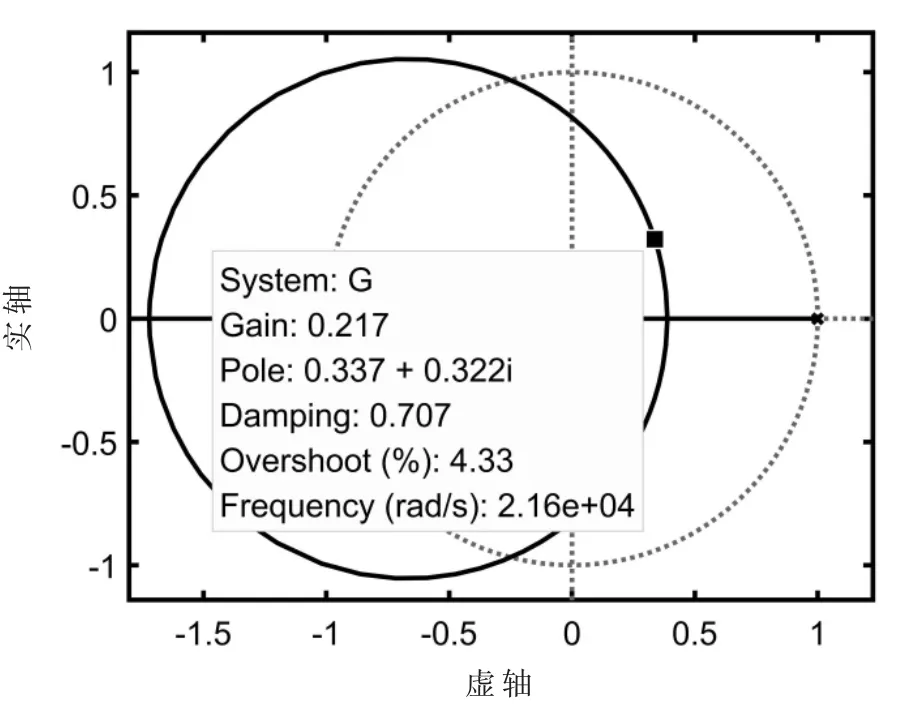
图6 电流内环开环根轨迹图

3.2 电压外环控制器设计

电流内环的响应速度比电压外环快5～10倍，因此在设计电压外环控制器时，可以将电流内环降阶，等效为一个一阶惯性环节Gi(s)，图7 所示为电流内环等效为一阶惯性环节后的电压外环结构图。

图7 等效后的电压外环结构图

图7 中D(s)为电压外环PI 控制器的传递函数，离散化后的传递函数为：

式中，ki和kp分别为PI 调节器的比例增益和积分增益。

由图7 和式(12)可得离散域中电压外环系统的开环传递函数为：

根据图8(a)和图8(b)可知，当开环零点Zo较小时，电压外环系统属于条件稳定系统。即使在满足系统稳定的条件下，由于系统的阻尼比太小，仍然无法满足系统动态性能指标；从图8(c)和图8(d)可以看出，随着开环零点Zo的不断增大，电压外环系统逐渐变成稳定系统，且开环根轨迹朝着阻尼比增大的方向移动，系统超调量相对减小，动态性能相对增强，取合适的阻尼比和Zo的值就能够使电压外环系统的动态性能满足要求。根据根轨迹法分析，取ξ=0.900，Zo=0.82，可得电压外环PI 控制器的参数为：kp=0.182，ki=0.0248。

图8 不同Z 值下的外环系统根轨迹图

4 仿真与实验

为了验证考虑数字延时环节的数字PID 控制算法在UPS 逆变控制系统中应用的效果，在MATLAB/Simulink仿真环境中对所提的方法与传统方法进行仿真对比分析。仿真参数如表1 所示。

表1 仿真参数

4.1 仿真分析

为了考察逆变控制系统静态稳定性能，在不同负载条件下，即纯阻性、阻感性、阻容性负载时，对逆变控制系统的输出电压的稳定性能进行仿真分析，仿真结果如表2、表3 所示。从表2、表3 可以看出，无论负载是纯阻性、阻感性或阻容性，考虑数字控制延时影响并修正控制器参数后的逆变控制系统的输出电压的稳态精度更高，THD 更小，且输出电压性能符合UPS 电源规格要求。

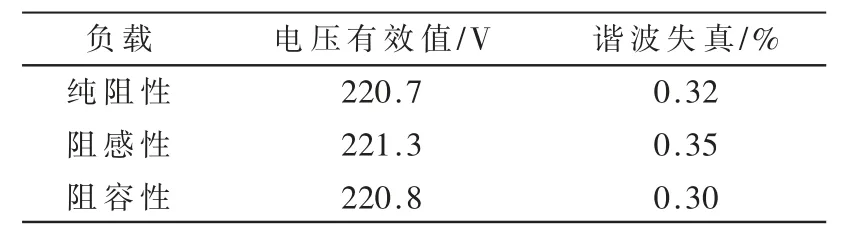
表2 考虑数字延时下逆变控制系统输出结果

表3 传统逆变控制系统输出结果

为了考察逆变控制系统的动态性能，对逆变控制系统进行突加突卸阻性负载的仿真分析，图9 为突加突卸阻性满载时的输出波形。系统开始处于空载状态，在0.005 s 时加载48.4 Ω 的阻性负载，考虑延时情况下，突加载恢复时间为1.1 ms，在0.015 s 时卸载,电压波形恢复时间为0.8 ms。没有考虑延时情况下，突加载恢复时间为2.3 ms，在0.015 s 时卸载，电压波形恢复时间为2.2 ms。从图9(a)、图9(b)对比可知，当考虑数字控制延时并修正PI 参数后，系统稳定性能更好，输出能够更快速响应负载端的变化，电压波形发生畸变后能够更快速恢复常态，响应时间更短。

图9 突加突卸阻性满负载时的输出波形图

4.2 实验验证

为验证本文设计的可行性和有效性，在以STMS32-F103C8T6 芯片为核心控制的逆变器样机上进行实验，试验参数和仿真参数相同，如表1 所示。

图10 为阻性的满载时的输出电压波形图，系统输出电压波形平滑，稳压精度小于1%，谐波失真小；图11为突加载时的输出电压波形图，当突加50 Ω 阻性负载时，瞬时电压跌落至285 V 左右，但是很快恢复正常，恢复时间为约为1.2 ms；图12 为突卸载时的输出电压波形图，当突卸50 Ω 阻性负载时，输出电压出现了285 V～334 V 的波动，但是约1.2 ms 之后电压恢复正常。从实验结果分析可知，考虑数字延时情况下，采用数字PID控制算法的逆变控制系统的动态响应速度更快，抗干扰能力更强。由于实验条件的限制，实验结果和仿真分析稍有差异，但是基本吻合，较好地验证了本文设计的正确性和可行性。

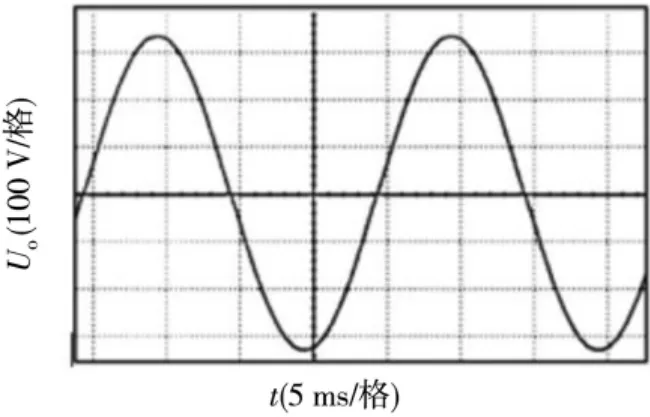
图10 带阻性满载时的输出电压波形图

图11 突加阻性满负载时的输出电压波形图

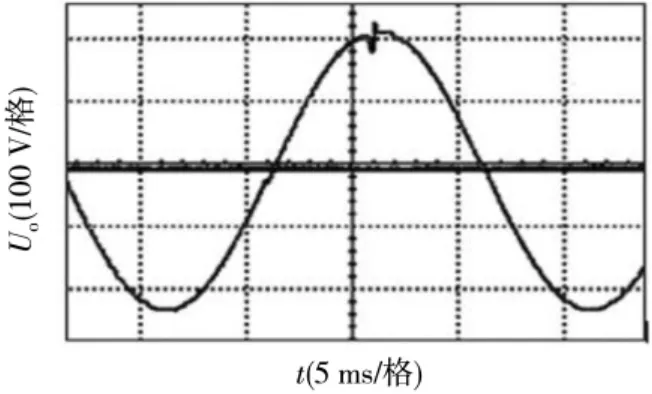
图12 突卸阻性满负载时的输出电压波形图

5 结论

本文针对单相UPS 逆变电源，对逆变控制系统中数字控制延时的影响进行了分析,忽略数字控制延时会对逆变控制系统的静态性能和动态性能产生负面影响。故可引入广义Z 变换来描述数字控制延时环节，改进控制系统的数学模型，修正数字PID 控制器参数，使系统具有更好的稳态特性以及动态响应性能。通过仿真分析和实验验证，得出以下结论：在考虑数字控制延时情况下，采用基于数字PID 的单相UPS 逆变控制系统的输出电压谐波失真更小，稳态精度更高，对负载的适应性更强；当负载端发生变化时，同时具有快速恢复波形畸变的能力，动态响应时间更短，具有较好的抗干扰性能。