应用局部样本最优K值KNN模型估测森林蓄积量1)

龚慧军 陈菊 熊伟华 王昊

(留坝县天然林保护工程管理中心，陕西·留坝县，724100) (留坝县桑元林场) (留坝县林业站) (留坝县天然林保护工程管理中心)

森林是陆地最重要的生态系统，也是地球中最大的有机碳库[1-2]。在中国西北地区，森林对生态环境的建设具有重要作用[3-4]。森林蓄积量是森林经营的重要内容，森林的结构参数是准确的估测森林蓄积量的基础，对于森林的经营管理有着重要的意义。

目前，森林蓄积量的获取主要是通过人工实地测量获取，人工实地测量不仅费时费力，而且效率低下。随着遥感技术的发展，可获取的遥感数据越来越丰富，利用遥感图像获取大范围、长时间的森林空间信息可以有效的提高森林资源调查的效率[5]。因此，将遥感数据与地面实测数据进行建模，从而推演出大尺度的森林蓄积量分布是未来森林蓄积量获取的主要手段。由于Landsat数据可以免费获取并且有着最丰富的数据积累，被广泛的用于森林蓄积量和生物量等重要的森林结构参数的估计。Zhao et al.[6]利用Landsat数据成功实现了生物量的量化和饱和值的估测；Aliny et al.[7]利用Landsat8 OLI估计了巴西桉树的森林蓄积量。在森林蓄积量的遥感估算研究中，模型的构建是影响估计精度的重要因素[8-9]。机器学习模型在定量遥感的研究中已经较为成熟，使用机器学习算法估计森林蓄积量的结果要明显优于传统的参数模型，因此，机器学习模型被认为是取代传统的参数模型的有效手段[10-11]。K-最近邻法(KNN)和随机森林(RF)是两种典型的机器学习算法，并且已广泛应用于森林蓄积量的估测研究。随机森林可以通过构建大量的回归树和分类树预测连续的未知变量，同时根据变量对误差的贡献程度输出所有参与建模变量的重要性[12]；K-最近邻法是根据训练样本和预测样本的变量计算样本间的距离，通过加权平均K个距离最小样本的观测值确定预测值[13]。KNN的最重要的两个参数是K值的选择和距离的度量[14]，欧式距离被用来衡量样本间的相似性，由于每个变量对距离度量的贡献相同，而距离度量方式忽略了变量与森林蓄积量的相关性。宋亚斌等[15]研究表明，利用光谱变量与森林蓄积量的相关性优化欧氏距离可以有效的提升KNN模型的估计性能。由于最终的预测值是由K个距离最近的样本的观测值加权平均获得，选择不同的K值则对KNN模型的性能产生较大的影响。理论上不同的样本可能对应不同的K值，然而多数的相关研究都是选择一个适合所有样本的最佳K值，不能充分的发挥KNN算法的性能。因此，本研究以陕西省留坝县为研究区，以lansdat8 OLI为数据源，开发了一种基于随机森林的局部样本最优K值KNN改进算法(LSO-KNN)，同时与RF、传统的KNN算法、距离加权KNN算法和多元线性回归模型进行对比，验证改进算法的可行性。

1 研究区概况

留坝县位于陕西省汉中市，地理坐标介于东经106°38′5″～107°18′14″，北纬33°17′42″～33°53′29″(见图1)。留坝县具有丰富的森林资源，树种以红桦(Betulaalbo-sinensisBurk.)、山杨(Populusdavidiana)、冷杉(Abiesfabri(Mast.) Craib)和栎类为主。土地总面积1 970 km2，林地面积1 816.74 km2，林木覆盖率92.97%。该地气候为暖温带湿润季风气候，系长江流域汉江支流。年平均日照时间1 804.4 h，年降水量为886.3 mm平均气温11.5 ℃，无霜期为214 d[16]。

图1 研究区位置

2 研究方法

2.1 遥感数据的获取及预处理

本研究中所使用的landsat8数据下载自地理空间数据云(http://www.gscloud.cn)，空间分辨率为30 m，包括蓝、绿、红等3个可见光波段，一个近红外波段和两个短波红外波段。采用ENVI5.3软件进行影像的预处理，包括大气校正、几何校正和地形校正。

2.2 地面数据统计

研究中所使用的地面数据来自2018年陕西省森林资源调查数据库中的样点调查数据，样点调查因子包括树种、胸径、树高和蓄积量等森林结构参数。利用二元材积方程计算每棵树的材积，样点的蓄积量由所有树种的材积求和，最后转化为公顷蓄积。地面数据包括228个样本，样地森林蓄积量最大值为283.00 m3/hm2、最小值为21.45 m3/hm2、平均值为81.50 m3/hm2、标准差为45.15 m3/hm2、变异系数为0.55。

2.3 遥感变量的提取与筛选

植被指数已经被用于森林参数的遥感定量研究[17]，并且地形对于森林参数也具有一定的影响值[17-18]。本实验共提取54个遥感变量，包括单波段变量、植被指数和地形因子。

表1 遥感变量

变量的选择对于森林蓄积量的建模起到决定性的作用，把全部遥感变量全部用于建模，会造成模型的可解释性降低，并且会把与蓄积量不相关的信息带入模型，导致模型具有较大的不稳定性[17-19]。目前，皮尔逊(Pearson)相关系数和主成分分析是一种较为流行的特征选择方式，但皮尔逊相关系数仅反映自变量与因变量间的线性关系，不能解释自变量与因变量间的非线性关系[19-20]。因此，本研究采用随机森林重要性(RFI)对所有变量进行排序，结合变异系数膨胀因素(VIF)对变量进行筛选，选择出对蓄积量影响较高的变量，同时剔除变量间的共线性。

2.4 模型的构建

2.4.1 KNN模型的构建

KNN算法最初由Cover和Hart于1968年提出[13]，是一种较为简单的机器学习算法。由于该算法不需要数据遵循正态分布，在使用KNN模型进行未知量的预测时具有很好的灵活性，并且已经被广泛的应用各类森林参数的制图中。它使用“特征相似性”原理从训练样本中选择与检验样本距离最小的K个样本，然后将K个样本的观测值以加权平均的方式赋值给检验样本。利用不同的K值重复上述过程对检验样本的森林蓄积量进行预测，均方根误差最小时，KNN模型所对应的K值被确定为最佳。

2.4.2 局部样本最优K值优化KNN模型

K值的选择对于KNN模型来说是最重要的一个环节，当前的KNN模型都是根据总体的最佳预测结果来确定一个整体的最佳K值，然而森林蓄积量的分布在空间上具有不稳定性，导致样本的总体最佳K值不适用于全区域的森林蓄积量反演[21-25]。为了优化K值的选择，在距离加权KNN模型的基础上，开发了一种基于随机森林的局部样本最优K值KNN算法(LSO-KNN)。首先，使用留一交叉的方法利用距离加权KNN模型对每一个样本进行预测，记录每个样本预测的最低均方根误差时所对应的K值；其次，将所有训练样本的最低均方根误差时所对应的K值作为因变量，Landsat8 OLI的光谱特征作为自变量，使用随机森林算法对每个样本的最低均方根误差时所对应的K值进行预测，得到每个样本的近似最佳K值，同时对整个研究区每一个像元的近似最佳K值进行预测，得到近似最佳K值的空间分布；最后将近似最佳K值和光谱变量集输入KNN模型实现最终的森林蓄积量预测，并绘制研究区森林蓄积量的空间分布。

2.5 精度验证

本研究中随机抽取2/3样本作为训练样本，用于训练模型的最佳参数，剩余1/3样本作为检验样本用于对模型进行精度验证及泛化性检验。采用均方根误差(RMSE)，相对均方根误差(RRMSE)和决定系数(R2)作为模型的检验指标，具体公式如下：

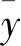
3 结果与分析

3.1 变量选择

本实验中根据随机森林重要性对63个特征变量进行排序并剔除变量自相关后，最终的变量选择红色波段(B4)、比值植被指数(IRV)、差值植被指数(IDV)、归一化植被指数(INDV)、增强植被指数(IEV)，各变量的重要值分别为0.21、0.16、0.14、0.18、0.09，其中，红色波段的重要性最高(RFI=0.21)，增强植被指数的重要性最低(RFI=0.09)，说明Landsat的红光波段对于森林蓄积量的变化较为敏感。

3.2 森林蓄积量估测

由表2可知，4种机器学习模型均取得了较好的拟合结果，其决定系数(R2)均大于0.50。其中LSO-KNN模型的决定系数最高(0.72)。相比于传统的多元线性回归模型，4种机器学习算法均表现出了更高的预测精度。其中KNN和RF得到了近似的估测结果，均方根误差分别为53.03和52.22 m3·hm-2；LSO-KNN模型得到了最佳的估计结果(RMSE=39.58 m3·hm-2，RRMSE=28.68%)。相比于其他3种机器学习算法，LSO-KNN算法的均方根误差分别降低了27.24%、24.23%和18.14%。

由图2可知，5种模型的残差图看起来具有相似的趋势，即低估了高蓄积量的样本和高估了低蓄积量的样本，这是光学数据在估计森林蓄积量中的局限行，也就是数据饱和问题。但是它们的取值范围差异较大。从图2-e2中可以看出，对于蓄积量较小的样本，LSO-KNN可以得到更准确的预测值，改善了低蓄积量样本的高估现象，原因是LSO-KNN算法对于低蓄积量的样本选择了更适合的K值，从而有效的提高了样本的估计精度。

表2 5种模型估测森林蓄积量的精度

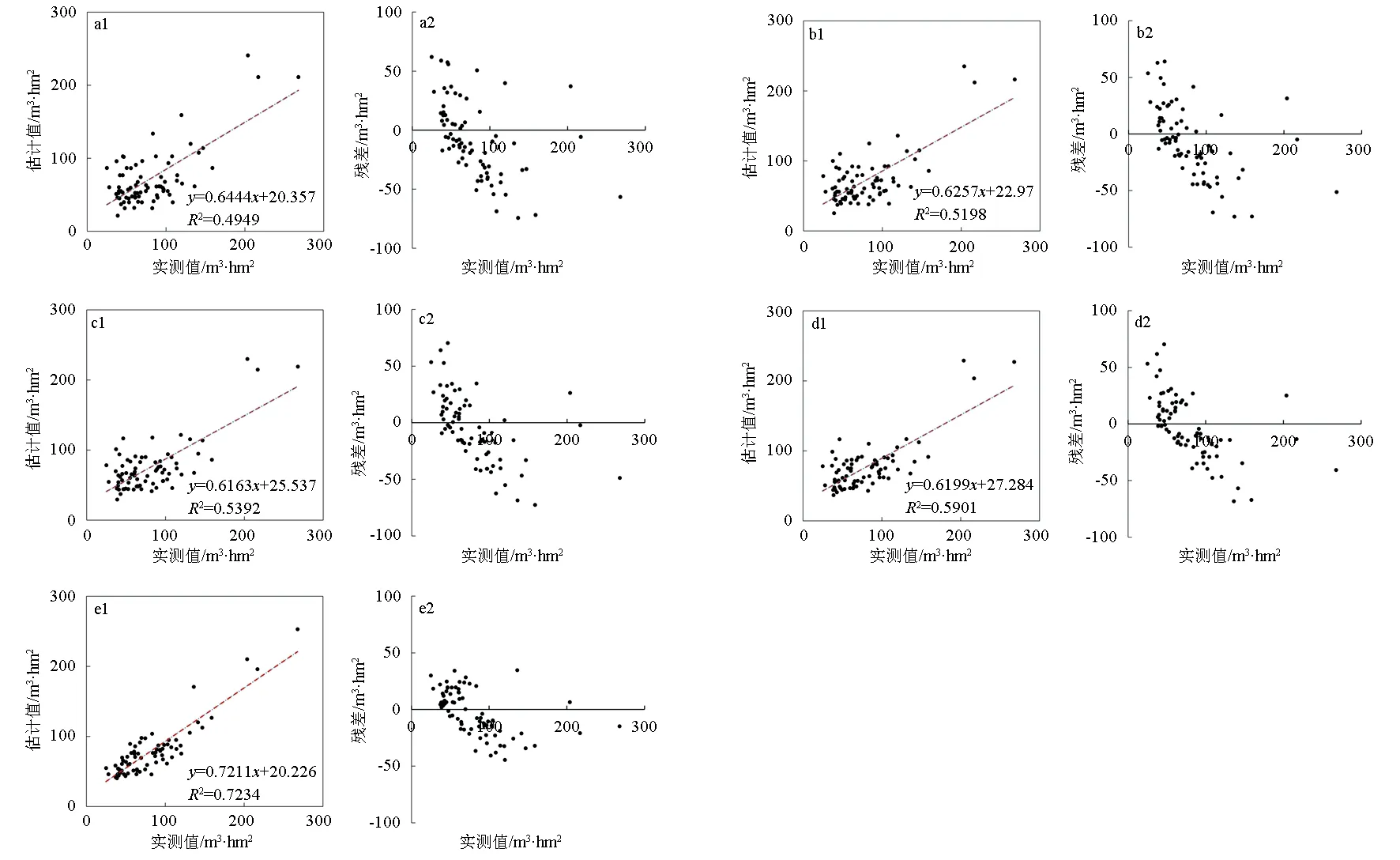
a为多元线性回归(MLR)，b为K最近邻(KNN)，c为随机森林(RF)，d为距离加权K-最近邻(DW-KNN)，e为局部样本最优K值KNN(LSO-KNN)。图2 5种模型估测结果的散点图及残差

3.3 留坝县森林蓄积量空间分布

由图3可知，使用Landsat8 OLI作为数据源，利用LSO-KNN模型对留坝县森林蓄积量进行反演的结果，留坝县东部和西部森林蓄积量较高，超过总量的70%以上，中部、南部森林蓄积量分布较低，此结果与实际调查基本一致。

4 结论

本研究以陕西省留坝县为研究区，以Landsat8 OLI为遥感数据源，分别构建了MLR、KNN、RF、DW-KNN和LSO-KNN 5种模型对森林蓄积量进行反演。4种机器学习算法的蓄积量估测结果均要优于多元线性回归模型，表明机器学习模型比于MLR模型具有更好的蓄积量估测潜力；LSO-KNN模型取得了本研究中的最佳估测结果(RMSE=39.58 m3/hm2)，说明通过优化K值的选择方式构建的LSO-KNN模型更适合森林蓄积量的估测。

图3 留坝县森林蓄积量分布