一道几何题的解法探究与反思

史增习

(浙江省慈溪市横河初级中学,315318)

2021年期末复习时,笔者评讲了一道几何题,在讲完这道题后,感觉意犹未尽,在课后作了进一步研究,并积累了一些心得.现将所得心得整理成文,与各位同行交流分享.

一、原题呈现

如图1,E,F,G,H分别是矩形ABCD四条边上的点,连结EG,HF交于点O,EG∥AD,FH∥AB,矩形BFOE∽矩形OGDH,连结AC分别交EG,FH于点P,Q.下列一定能求出∆BPQ面积的条件是( )

(A)矩形BFOE和矩形OGDH的面积之差

(B)矩形ABCD与矩形BFOE的面积之差

(C)矩形BFOE和矩形FCGO的面积之差

(D)矩形BFOE和矩形AEOH的面积之差

二、总体分析

这是一道以相似矩形为背景的具有宁波特色的PISA题,旨在考查学生观察能力、逻辑推理能力、计算能力等核心素养,同时要求教师在教学过程中,应把握问题实质,实施针对性、导向性教学,让学生跳出题海烦恼.

三、解法探究

1.代数法

解法1设OH=a,OG=b,矩形BFOE与矩形OGDH的相似比为k,则BE=ka,BF=kb.

∵EP∥BC,∴∆AEP∽∆ABC,

∴EP=b,PO=kb-b.

同理,可得QF=a,OQ=ka-a,

∴S阴影=S矩形EBFO-S∆EBP-S∆BFQ-S∆POQ

而k2ab为矩形EBFO的面积,ab为矩形HOGD的面积,故答案选A.

2.几何法

解法2如图2,连结EH，HG.

由矩形BFOE∽矩形OGDH,可得矩形ABCD∽矩形HOGD，∴∆ADC∽∆HDG,∴∠DAC=∠DHG,∴HG∥AC.

∵EG∥BC,∴∠HGO=∠APE=∠ACB,

∴∆HOG≌∆AEP≌∆QFC,

∴S∆HEG=S∆QBC.

∴S阴影=S∆PBC-S∆QBC=S∆PBC-S∆HEG

∵矩形HOGD∽矩形EBFO,

∴OG·OF=HO·AH,

即S矩形OFCG=S矩形AEOH,

故答案选A.

解法3不难发现,∆BPQ是两个大∆ABQ与∆PBC的重叠部分,

∴S阴影=S∆ABQ+S∆PBC-S∆ABC

故答案选A.

四、解题反思

1.对于PISA题,我们通常可以从代数和几何两个视角入手解决.代数法只要增设一些变量,虽然思维含量小,操作相对简单,但在解题过程中,往往计算量较大,对考生的计算能力有较高的要求.而几何法,思维含量大,旨在考查学生的观察能力和逻辑推理能力等思想方法,但一旦想到,答案水到渠成.以上两种方法各有千秋,在平时教学中,教师应多引导、多比较.

2.由解法2,可知相似矩形(多边形)的知识,往往通过添加辅助线,利用边、角关系,化归为相似三角形、全等三角形等知识.在九上“相似多边形”的教学中,很多教师为了赶进度,只要求学生机械记忆相似多边形的边、角性质,并配套一些简单的题目加以巩固,草草了事.这种教学方式,学生只能解决一些简单的题目,并没有把学生的思维向深度发展,一旦遇到综合题,学生就束手无策了.因此,在平时教学中,教师应多研究教材,多总结思想和方法,多整合教学资源.

3.由解法3,不难发现条件“矩形BFOE∽矩形OGDH”多余.因此,我们可弱化条件,把此题改为:如图1,E,F,G,H分别是矩形ABCD四条边上的点,连结EG,HF交于点O,EG∥AD,FH∥AB,连结AC交EG,FH于点P,Q.下列一定能求出∆BPQ面积的条件是( )

(A)矩形BFOE和矩形OGDH的面积之差

(B)矩形ABCD与矩形BFOE的面积之差

(C)矩形BFOE和矩形FCGO的面积之差

(D)矩形BFOE和矩形AEOH的面积之差

由解法3,利用几何法已经得证.现通过代数法进行证明.

设OH=a,OG=b,OE=c,OF=d.

∵EP∥BC,∴∆AEP∽∆ABC,

∴S阴影=S矩形EBFO-S∆EBP-S∆BFQ-S∆POQ

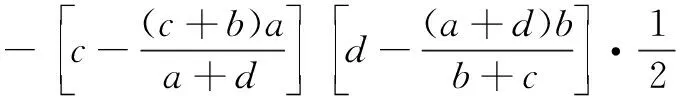
故答案依旧是A,说明原题中相似条件是多余的.

解题是数学教师的基本功,教师良好的解题能力将直接影响学生的解题水平和思维能力的培养.在平时教学中,教师不应就题论题,而应从多角度去分析问题,并及时总结思想方法,逐步培养学生发现问题、分析问题、解决问题的能力,让学生真正脱离题海战术,把核心素养落实到教学实处.