基于Sobol’法的转轮叶片动态响应灵敏度分析

李兆军，张光政，刘福秀，丁 江

（广西大学机械工程学院，广西南宁 530004）

0 引言

水轮发电机组在运行过程中的工况复杂多变，致使水流常常处于非稳定状态，从而使转轮叶片在复杂的水流激励作用下产生剧烈振动，影响水轮机的安全稳定运行［1］，因而实现转轮叶片振动特性的有效调控使其振动特性满足水轮机正常工作是十分必要的。目前，学者们对转轮叶片振动特性控制方面的研究主要是集中在如何避免转轮叶片产生水力共振等方面。例如，史广泰等［2］采用ANSYS 平台对水轮机转轮进行了模态计算和振动分析，分析了机组产生共振的运行条件；李海亮等［3］采用有限元法研究了混流式水轮机转轮振动特性以及各部件对转轮固有频率的影响规律；张新等［4］为了使转轮的固有频率避开外界的激振频率，利用CFD 软件对水轮机转轮进行了有限元模态分析。但这些研究均未讨论转轮叶片振动特性对工况参数的敏感程度。

动态响应灵敏度能够反映设计变量或者参数对结构振动指标的影响，许多学者开展了相关方面的研究，例如，孙维光等［5］基于Sobol’法推导了动力包机组振动对悬挂隔振参数的全局灵敏度；王长科等［6］对列车车体的扭转振动进行了灵敏度分析，得到了对车体扭转振动频率影响较大的设计参数；刘柏希等［7］利用偏导数法分析了RV 减速器系统固有频率对转动惯量和刚度的影响。因而，积极开展水轮机转轮叶片动态响应灵敏度方面的研究对于有效控制转轮叶片振动特性具有十分重要的意义。然而，目前关于转轮叶片动态响应灵敏度问题的研究鲜见文献报道。

本文以水轮机转轮叶片为研究对象，根据转轮叶片的动力学模型，得到转轮叶片的动态响应表达式，在此基础上利用Sobol’法推导转轮叶片动态响应对工况参数的灵敏度，揭示工况参数对转轮叶片动态响应的影响，并通过实例进行分析。

1 转轮叶片动力学模型

考虑到转轮叶片的几何形状以及在工作过程中的受力情况，其往往会发生弹性变形，故将转轮叶片视为弹性体，采用矩形平面壳单元进行转轮叶片的模拟。利用有限元法，建立转轮叶片的动力学方程为［8］：

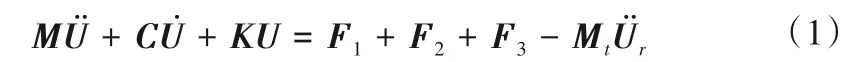
式中：M为转轮叶片整体质量矩阵，且M=Mt+Mp；Mt为单元的质量矩阵；Mp为附加质量矩阵，与水力参数有关，因而质量矩阵M不仅与转轮叶片的结构参数有关，而且还和水力参数有关，为流固耦合项；K为转轮叶片整体刚度矩阵；C为转轮叶片阻尼矩阵；、、U分别为系统广义位移向量、广义速度向量、广义加速度向量；Mtr为转轮叶片的自激惯性力项，它不仅与转轮叶片的运动参数有关，而且还与转轮叶片的结构参数和水力参数有关，为流固耦合项；F1为卡门涡引起的压力脉动，可由文献［9］确定，F2为尾水管涡引起的压力脉动，可由文献［10］确定，F3为动静干涉引起的压力脉动，可由文献［11］确定。

根据动力学方程，转轮叶片频率方程可表示为：

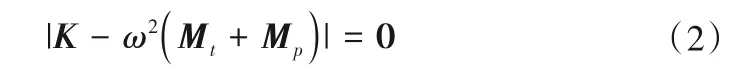
根据式（2），即可求出转轮叶片的固有频率。进一步，利用振型叠加法求解出转轮叶片的振动响应：

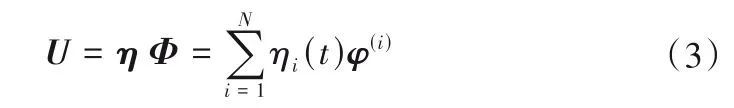
式中：N为转轮叶片自由度数；Φ为正则模态矩阵；η为相应的模态坐标列阵。

2 动态响应灵敏度分析

灵敏度分析可以反映输入变量对输出变量的影响程度，从数学上可表示为：若某一函数f（x）可导，则其一阶灵敏度可表示为［12］：

式中：xi为所分析参数变量的集合；S又称f（x）对xi的一阶微分灵敏度。

这里采用Sobol’法来推导转轮叶片动态响应对工况参数的灵敏度，Sobol’法是一种基于方差的蒙特卡洛法，其大致过程如下所示［13］：

首先，将转轮叶片动态响应表示为U=f(X)，其中X=(x1，x2，…，xk)为影响转轮叶片动态响应的k个工况参数所组成的参数向量，进而可建立输入参数的空间域为Pk。

其次，将f（X）表示为2k个递增项之和，即：

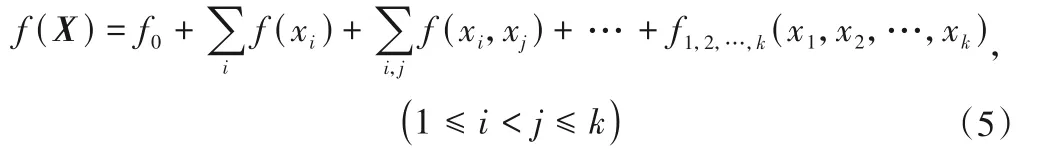
式中：f0为常数。其余子项对其所包含的变量的积分一定为零，即：

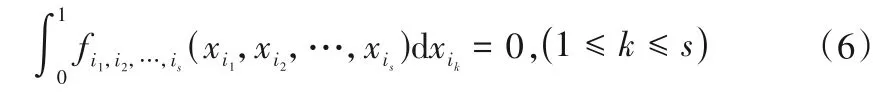
根据式（5）和（6），可以看出各项之间都是正交的，如果(i1，i2，…，is) ≠(j1，j2，…，jn)，有：

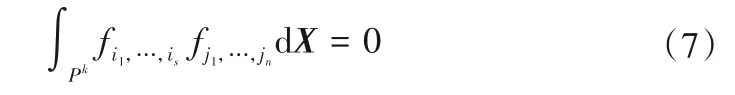
进一步有：

对式（5）取多重积分，即可得到各子项的表达式：

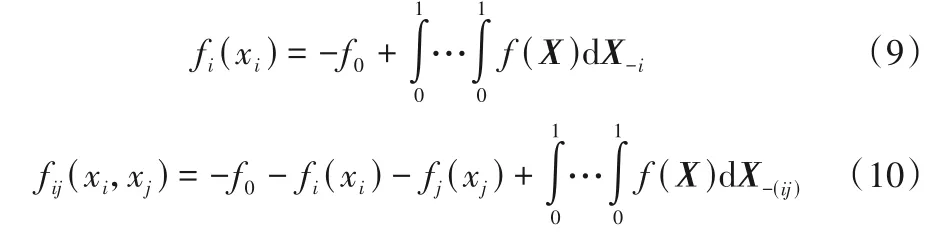
式中：X-i表示xi之外的其他工况参数，同理X-(ij)表示xi和xj之外的其他工况参数。

基于上述推导，可得到函数的总方差和偏方差的表达式为：

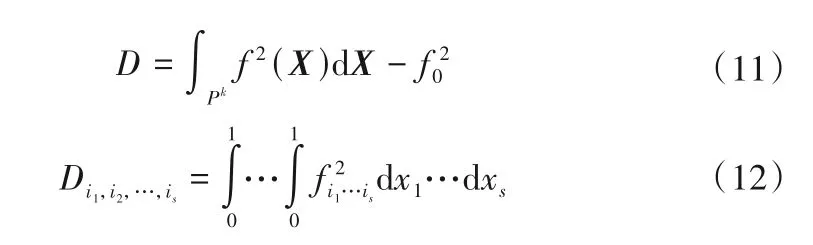
最后，各工况参数变量对转轮叶片动态响应的灵敏度可表示为：

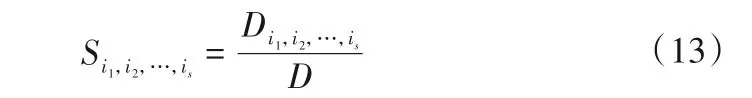
式中：Di1，i2，…，is和D分别为f（x）的偏方差和总方差；Si1为转轮叶片动态响应对工况参数x1一阶灵敏度，反映x1单独变化对转轮叶片动态响应的影响，同理可得其他转轮叶片动态响应对其他工况参数变量的一阶灵敏度。

3 实例分析

以国内某700 MW 大型混流式水轮机为例，主要计算参数如下：额定转速n=107.14 r∕min；额定流量Q=554.52 m3∕s；额定负荷W=571 MW；转轮最大外径为D=8 051.8 mm；转轮叶片数Z1=13，单个转轮叶片的质量mt=7.7 × 103kg，转轮叶片的材料密度为ρ=7.85×103kg∕m3，转轮叶片的弹性模量为E=210 GPa，泊松比μ=0.3；导叶数Z2=26；转轮叶片出水边厚度δ=0.026 m；转轮叶片出水口流角β=20°；斯特鲁哈数sh=0.26；转轮叶片尾部形状影响系数k=2.4。考虑到水轮机工况参数较多，这里选择一个易于控制的工况参数（转速）进行分析，假设转速的变化范围为0.5n至1.2n，转速每上升0.1n取一个转速点进行分析，共8 个转速点，记为ni（i=1，2，…，8），为了简化计算，这里假设ni服从均匀分布，且取值范围为［ni-0.02n，ni+0.02n］，如表1 所示。采用拉丁超立方采样法对ni进行采样，采样次数设置为2 000次，并基于Sobol’法计算转轮叶片动态响应对转速的灵敏度，如图1所示。

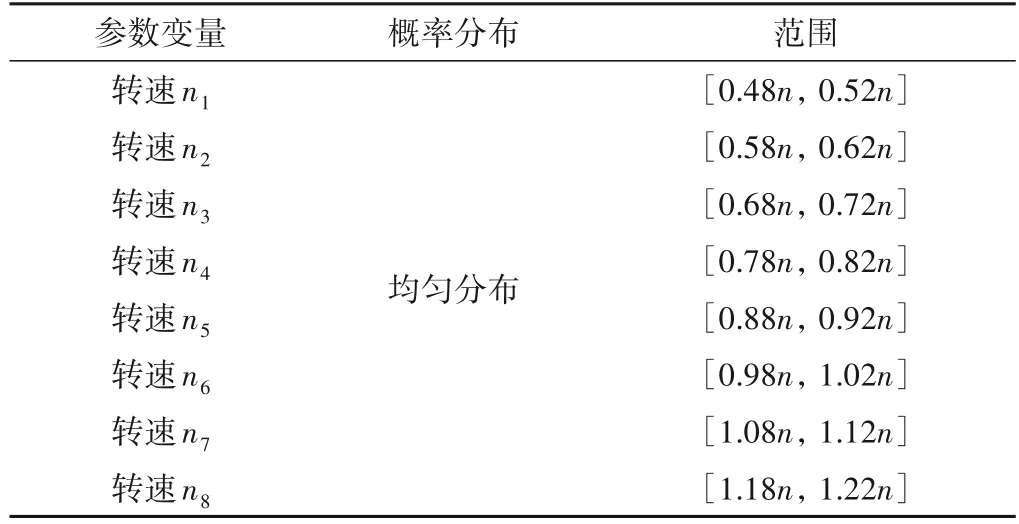
表1 转速概率分布 r∕minTab.1 Probability distribution of speed

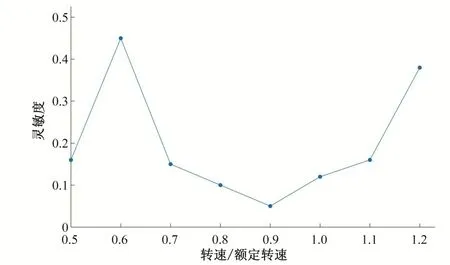
图1 转轮叶片动态响应对转速的灵敏度曲线Fig.1 Sensitivity curve of blade dynamic response to speed

从图1 中可以以看出，在转速从n1变化至n8的过程中，转轮叶片动态响应对转速的灵敏度呈先增大后减小再增大的趋势，当转速变化至n6（0.6n）以及n8（1.2n）时，转轮叶片动态响应对转速的灵敏度出现了两个峰值，说明在这两个转速附近转轮叶片动态响应对转速的变化是较为敏感的。

从上述分析可以看出，转速对转轮叶片动态响应的影响是随转速的大小而不断变化的，如果要想实现在水轮机运行过程中对转轮叶片振动的控制，应关注灵敏度较大的两个位置，即转速为n6和n8。

为了验证仿真结果的正确性，进行了水轮机变转速实验，首先进行测点及装置布置，即在转轮叶片上布置应变片，并将应变信号采集仪安装在主轴轴顶；然后让水轮机分别在每个转速下运行并采集动应力信号；最后进行数据处理并计算动应力通频值，通过试验采集得到转轮叶片出水边某一测点的动应力峰峰值随转速的变化曲线，如图2所示。

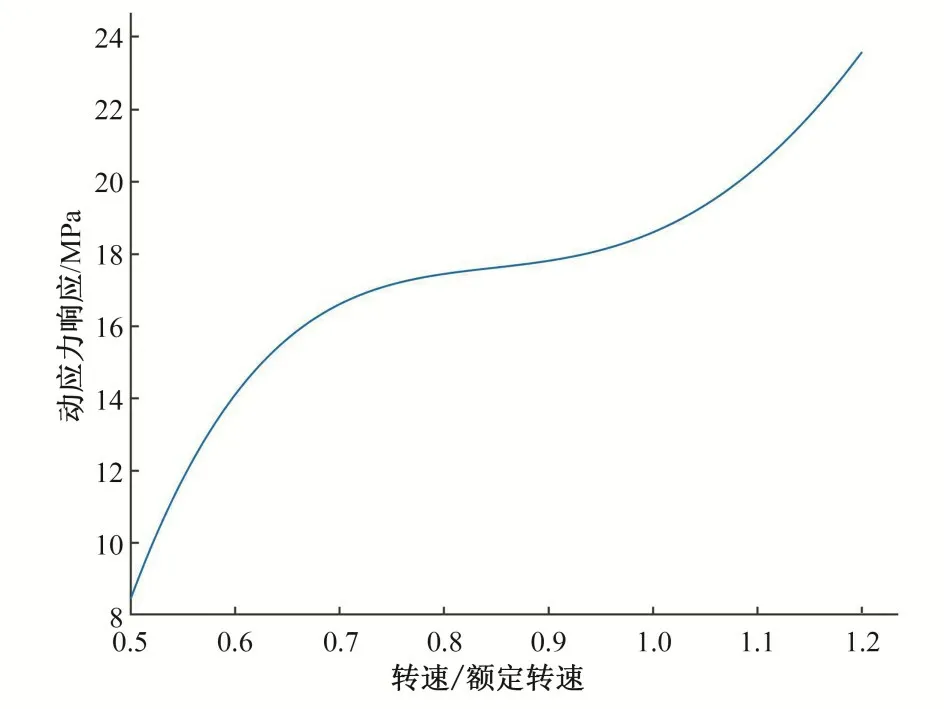
图2 转轮叶片动应力随转速的变化曲线Fig.2 Variation curve of dynamic stress with rotating speed

从图2 中可以看出，随着转速∕额定转速的增大，转轮叶片的动应力响应也随之增大，当转速比在［0.8，1］这一区间内，转轮叶片动应力响应上升较为缓慢，处于一个较为稳定的状态，总的来说，转轮叶片动应力响应随机组的转速的增加而单调上升。

根据图2 所示试验所测得的转轮叶片动应力随转速的变化曲线，计算其每个转速比处的斜率，并进行归一化处理，得到转轮叶片动应力对转速的灵敏度曲线，并将仿真得到曲线与其进行对比，如图3所示。

从图3 中可以看出，通过实测数据绘制成的灵敏度曲线和仿真所得到的灵敏度曲线基本一致，其峰值都出现在转速为n6和n8处，只是灵敏度的大小有所差异。此外，该灵敏度曲线也与图2 中转轮叶片动应力随转速的变化趋势较为符合，故可以说明本文通过仿真计算得到的结果是较为准确的。根据灵敏度分析的结果，可得到对转轮叶片动态响应变化最敏感的转速范围，从而为转轮叶片的振动控制提供依据。

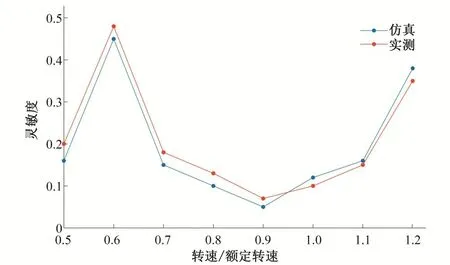
图3 转轮叶片动应力对转速的灵敏度曲线Fig.3 Sensitivity curve of blade dynamic stress to speed

4 结论

Sobol’法是一种基于方差的蒙特卡洛法，采用Sobol’法能够有效地分析和计算转轮叶片动态响应对工况参数的灵敏度。首先，建立转轮叶片的动力学模型，推导转轮叶片动态响应与各相关参数的内在关系式，并构建相关输入参数的空间域；然后，将转轮叶片的动态响应函数式表示为2k个 递增项之和，并且使各项之间都是相互正交的；最后，基于转轮叶片动态响应函数的总方差和偏方差表达式，得到转轮叶片动态响应灵敏度计算公式。实例分析结果表明，转轮叶片动态响应对转速的灵敏度呈先增大后减小再增大的趋势，在转速∕额定转速为0.6 以及1.2 时，转轮叶片动态响应对转速的灵敏度出现了两个峰值，说明在这两个转速附近转轮叶片动态响应对转速的变化是较为敏感的。本文的研究为进一步深入分析转轮叶片的振动特性与工况参数之间的内在关系提供一个可行的方法。