基于水文-气象因子的综合多模型长期径流预报研究

李福威，包爱美，疏杏胜，丁 伟

（1.国电电力和禹水电开发公司，辽宁本溪 117201；2.大连理工大学水利工程学院，辽宁大连 116024）

0 引言

长期径流预报对掌握未来径流信息，实现水资源的高效利用、水电站优化运行、防汛抗旱等具有重要意义。然而，由于长期预报的预见期较长，其受大气环流、下垫面情况、人类活动等多重因素影响［1］，径流过程的不确定性大，预报难度较大，预报精度难以保证。目前，对于降低较长预见期径流预报的不确定性、提高预报精度的研究，主要考虑两个方面，一是预报因子筛选方面，探究径流形成的物理基础和影响径流变化的各因素及其间的相互作用，从众多因子中筛选出与预报对象密切相关的因子；二是预报模型方面，研究预报模型的方法原理及其适用性，进行多模型的比较分析和综合利用。

随着中长期径流预报研究的快速发展，可利用预报方法较多，主要分为两类，一类是根据径流序列自身规律，仅考虑径流单要素作为预报因子的历史演变法、时间序列法等传统统计方法［2-4］；一类是挖掘水文和气象数据的潜在规律，考虑水文、气象等多要素作为预报因子的回归分析法和机器学习法。后者可选用一切与预报对象存在潜在关系的影响因素［5］，包括考虑入海平面气压、大气环流因子等气象因子用作预报因子来实现对流域径流的预报，具有较强的物理基础，获得较长的预见期和相对较高的预报精度［6-8］。朱春苗等［9］利用相关系数法、主成分分析法和互信息法优选松花江流域上游3个水文代表站的预报因子，采用SVR（Support Vector Regression）模型进行流域月径流预报，得出适用于该流域月径流预报的最优预报因子组合模型。雷莉和王超［10］从130项气候系统指数中筛选出预报因子后，基于筛选的因子构建了石羊河流域BP-ANN（Back Propaga‐tion-Artificial Neural Network）、Elman 和PSO-SVR（Particle Swarm Optimization-SVR）三种年径流预报模型并比较各模型预报结果，确定Elman 和PSO-SVR 中长期径流预报模型可为该流域中长期径流预报提供支撑。李伶杰等［11］以龙江水库入库径流预报为研究对象，从环流指数、海温、气压和前期月径流中选取关键预报因子，建立随机森林与支持向量机模型，发现太平洋中北部与西部气候因子对径流预报的影响较大。

考虑到长期径流预报受影响因素多，预报不确定性较大的问题，本研究以浑江桓仁水库年入库径流和汛期月入库径流预报为研究对象，考虑将前期降雨、径流作为预报因子的同时引入大气环流因子，建立包括统计分析法和机器学习法的多个长期径流预报模型，比较各模型在桓仁流域的适用性，并分析各模型对年径流预报及汛期各月径流预报的预报水平，给出最优预报方案，提高桓仁流域长期径流预报的精度。

1 材料与方法

1.1 研究区概况及数据资料

桓仁水库作为浑江梯级电站的龙头水库，总库容为36.4 亿m3，电站装机容量为222.5 MW，兼有防洪、灌溉等综合作用。桓仁水库以上流域有中小水库共47 座，总库容合计2.43 亿m3，其中中型水库6 座，总库容1.96 亿m3，占比80.7%，小型水库41座，库容0.48 亿m3，占比19.3%。流域多年平均年降水量860 mm，降水年内分配不均，70%的雨量集中在6-9 月间，且在7、8月达到最大，大洪水主要发生在7 月下旬至8 月中旬；冬季一般从11 月份开始到翌年3 月末或4 月初结束，期间主要以降雪为主，受积雪影响，冬季径流一般较枯。因此，桓仁水库来水从5月份流域发生春汛开始一直持续到10月份，汛期作为桓仁水库年内主要来水阶段，充分把握汛期各月来水情况，对于电站做出全局较优的发电调度过程，提升发电效益具有重要意义；而年径流预报可为水库运行管理提供更长远的参考信息，帮助管理者更早地制定调度计划，从而更高效地利用水力资源。

径流资料来源于桓仁水库1967-2017 年月实测入库流量，1967-2017 年74 项大气环流因子的逐月数据源自国家气候中心网站（http：∕∕www.ncc-cma.net∕cn∕），桓仁水库流域1967-2017年逐月实测降雨量源自中国气象数据网（http：∕∕data.cma.cn∕）。

1.2 研究方法

1.2.1 预报因子筛选

（1）因子初选。采用相关系数法对预报因子进行初选，按照相关性大小分别从诸多水文、气象因子选取预报因子。由于预报因子对径流的影响存在滞后效应，预报年径流时，水文因子取桓仁水库预报年份前3 年的实测年降雨量与年径流量，气象因子取预报时刻前一年内国家气候中心各月份发布的74 项大气环流因子。预报月径流时，前12 个月的水文、气象因子作为输入因子。相关性系数计算公式为：

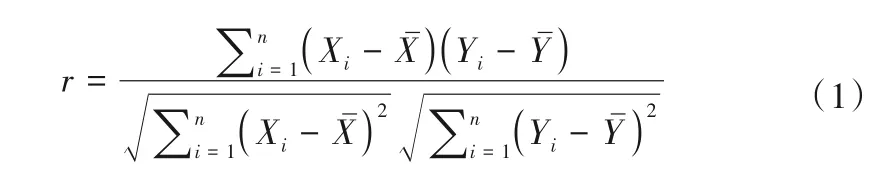
式中：r为相关系数；n为资料样本数；Xi与分别为输入因子及其序列均值；Yi与分别为预报对象及其序列均值。r的取值范围为［-1，1］，其正负号表示两变量之间是正相关还是负相关，绝对值越接近1表明两变量的线性相关程度越高。

（2）因子精选。在使用相关系数法初选出因子后，进一步结合预报模型分析不同因子组合对模拟和检验结果的影响，以确定最终的预报因子。本文采用向前搜索包裹法，以率定期残差平方和最小为目标，通过评价预报模型在不同因子组合情况下的预报结果，确定最优预报因子组合，具体步骤如下：

①将初选因子相关性系数排序第一的因子x0作为固定因子，分别与其他因子组合输入到预报模型，选择率定期的残差平方和f(x0，xi)最小时加入的因子xi作为选定因子。

②以x0、xi为固定因子，分别与其他因子组合输入到预报模型，确定使f(x0，xi，xj)最小时的因子xj，若f(x0，xi，xj)小 于f(x0，xi)，则将xj因子加入模型，进行步骤③；否则，排除该因子。

③重复步骤②，不断增加输入因子个数，直至f不再减小或者f的递减速度小于一定程度时，从而确定出最终预报因子集。

1.2.2 预报模型构建

选用多元线性回归（Multiple Linear Regression，MLR）［12］、多元门限回归（TR）［13］、逐步回归（Stepwise Regression，SR）［14］、人工神经网络（Back Propagation-Artificial Neural Network，BPANN）［15］、支持向量机（Support Vector Machine，SVM）［16，17］和基于主成分分析的人工神经网络模型（Artificial Neural Network Model based on Principal Component Analysis，PCA-BP-ANN）六个模型，以最终筛选的水文、气象因子为模型输入，以预报径流的合格率（QR）为评定指标，分别构建桓仁水库流域年径流预报模型和汛期月径流预报模型。据《水文情报预报规范GB∕T 22482-2008》，许可误差限为多年同期变幅的20%，桓仁水库年径流多年变幅的20%为14.9 亿m3，汛期各月的允许误差（已转化为流量）见表1。

表1 汛期各月允许预报误差 m3∕sTab.1 Allowable forecast error of each month in the flood season

多元线性回归（MLR）、多元门限回归（TR）、逐步回归（SR）等传统统计模型在中长期径流预报中应用较早，其结构简单、易于操作，只需确定各预报模型数学方程，即可得到较好的预报效果。人工神经网络（BP-ANN）和支持向量机（SVM）作为在中长期径流预报中应用最广泛且较成熟的机器学习模型，具有较强的非线性映射能力，相对传统的统计方法，能够更好地刻画径流过程非线性及非稳态性的特点。选用具有3层网络结构（输入层、隐含层和输出层）的人工神经网络（BP-ANN）模型，以年径流预报合格率为指标，采用试错法确定网络隐含层，并经反复训练确定每层结构所含神经元的个数；SVM 模型能够快速处理小样本的非线性问题，具有较强的泛化能力，模型需确定的参数有惩罚函数C、不敏感损失系数ε、核函数及其所含参数g，本文采用试错法确定核函数，并采用网格搜索法优化确定惩罚系数C和核函数参数g。

主成分分析（Principal Component Analysis，PCA）法是通过解析原来具有一定相关性的多变量，将原变量进行线性组合导出一组新的综合变量，使这些新的综合变量能够尽可能多地反映原始变量的信息，以达到简化数据和降维的目的［18］。本文构建基于主成分分析的人工神经网络模型（PCA-BP-ANN）时，采用PCA 法将筛选后的预报因子重新组合为新的变量，并根据计算的特征值、方差贡献率和累积贡献率确定主成分个数，以新确定的主成分作为输入因子输入到BP-ANN 模型进行径流预测。

2 结果与分析

2.1 预报因子筛选

（1）因子初选。考虑水文和气象两类因子对径流变化的影响，采用相关性分析法分别对流域水文、气象因子进行初选，取相关性系数较大的因子作为备选因子。对桓仁水库流域月径流量与前期各月份实测降雨、径流和大气环流因子进行相关性分析，得到该流域长期径流预报的备选因子，结果见表2 和表3。由表可知，对于月径流，除了上月月降雨量相关性系数达0.57，其他水文因子与预报对象的相关性都低于备选的大气环流因子；对于预见期更长的年径流，虽然大气环流因子与年径流的相关性系数相对月径流有所减小，但其与预报对象的相关性依旧远高于水文要素。

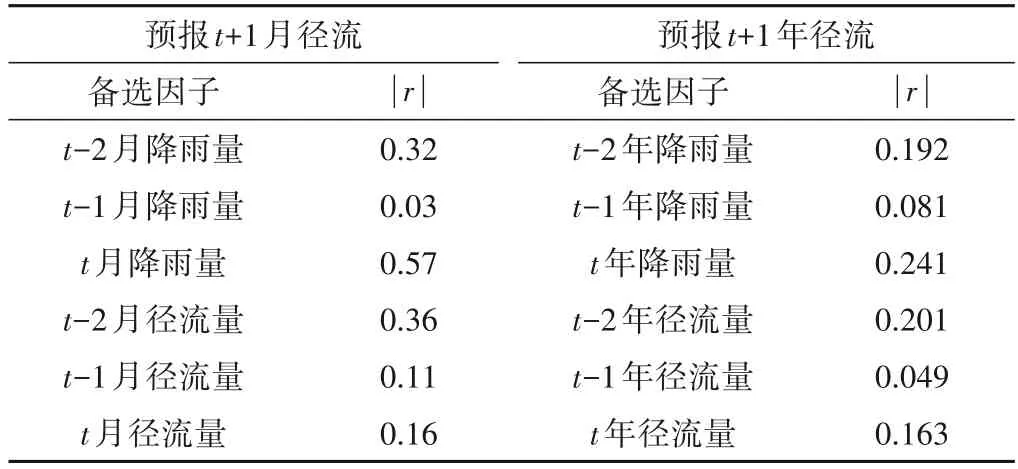
表2 相关性较高的水文因子Tab.2 Hydrological factors with high correlation

（2）因子精选。结合所选预报模型，采用向前搜索包裹法，对表2 和表3 确定的备选因子进一步筛选，分别确定各预报模型的最优组合因子作为各模型的最终输入因子，表4 列出了结合多元线性回归预报模型确定的最终预报因子，以此作为多元线性回归预报模型的输入，同理可确定其他预报模型的最终预报因子。

表3 相关性较高的大气环流因子Tab.3 Atmospheric circulation factors with high correlation

采用主成分分析（PCA）法将表4 中选定的预报因子进行线性组合，使其成为一组新的线性无关的综合变量，并根据特征值的累积贡献率达90%确定主成分个数，各成分的特征值及其方差贡献率和累积贡献率结果见表5。由表5 可知，对于汛期月径流预报，前3 个主成分的累积贡献率为90.5%，而后3 个主成分的贡献率较低，对汛期月径流预报的影响不大，因此选定前3 个主成分为模型输入，式（2）～（4）分别给出了3 个主成分与标准化原始变量的关系；对于年径流预报，前5个主成分的累积贡献率才能达90%以上，即需要5 个主成分方可有效地代表原始变量90%以上的信息。此外，年径流预报确定的主成分个数比月径流预报多，说明预报预见期更长的年径流所受影响因素要比预报月径流更为复杂，其预报不确定性更大。

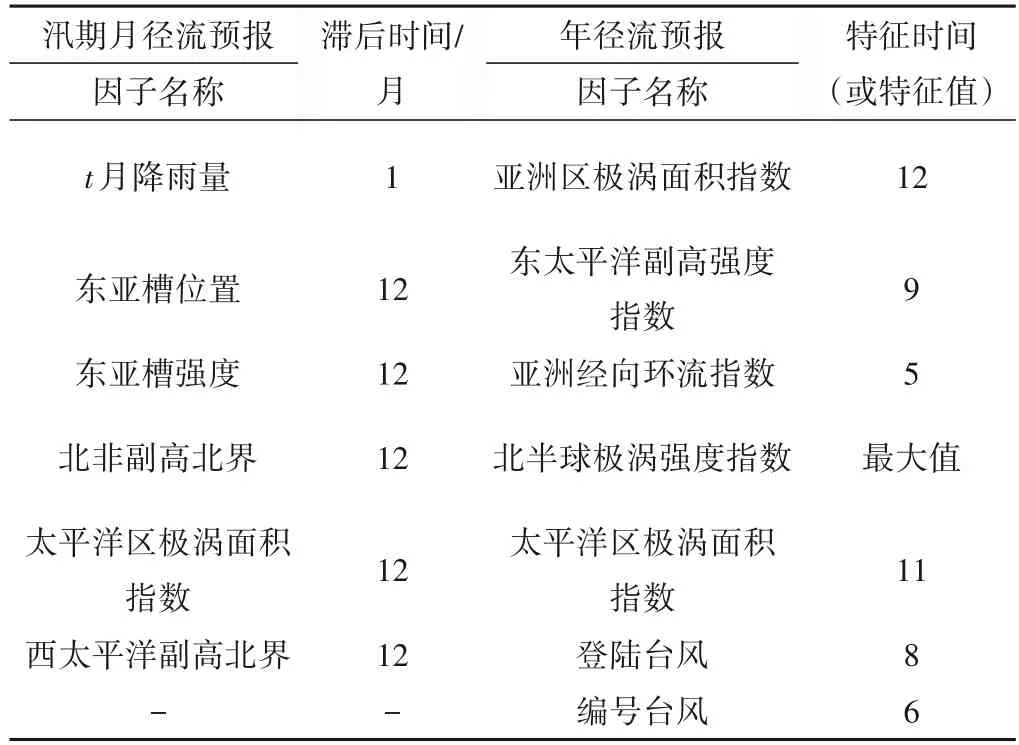
表4 多元线性回归预报模型最终预报因子Tab.4 Determined predictors

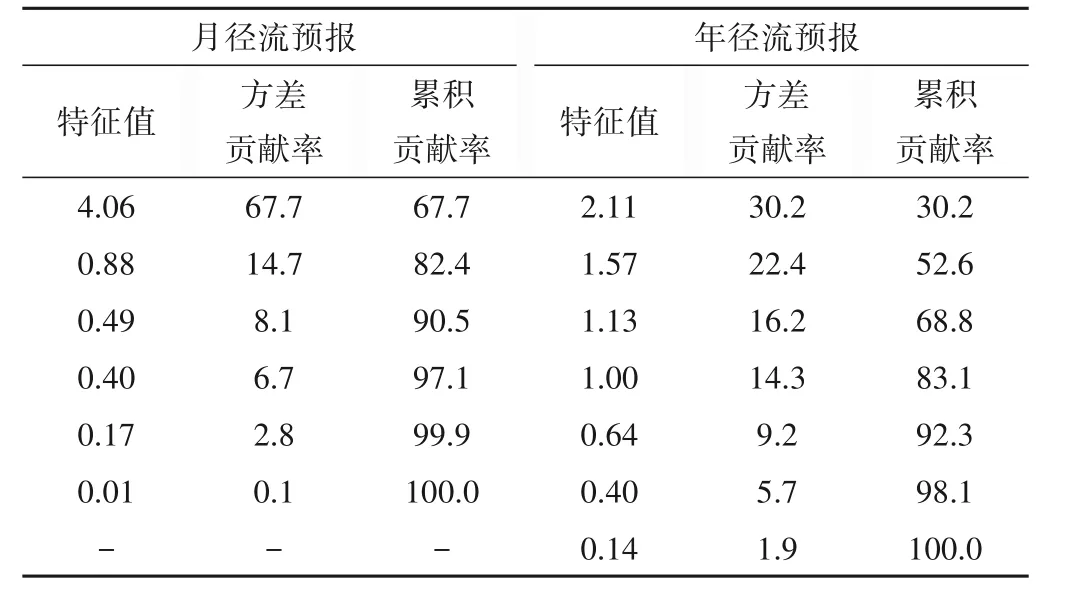
表5 应用PCA法计算的各成分特征值、方差贡献率和累积贡献率%Tab.5 The eigenvalues，variance contribution rate and cumulative contribution rate of each component calculated by PCA method

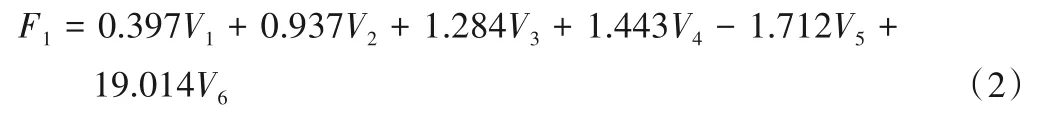
式中：Fi（i=1，2，3）表示主成分；Vj（j=1，…，6）表示标准化原始变量。

2.2 模型构建及预报效果分析

将桓仁水库流域实测径流资料以及选中的预报因子划分为率定期和验证期两部分，率定期为1967-2000 年，验证期为2001-2017 年，以预报径流的合格率（QR）为评定指标，分别构建多个桓仁水库流域长期径流预报模型并验证。式（5）和式（6）分别给出了流域汛期月径流和年径流的多元线性回归模型（MLR）预报方程，而多元门限回归（TR）和逐步回归（SR）方法类似；表6 展示了人工神经网络（BP-ANN）和支持向量机（SVM）两机器学习模型的参数结果；采用主成分分析（PCA）结果，将月预报确定的3 个主成分和年预报确定的5 个主成分分别输入到BP-ANN模型中，构建月径流预报PCA-BP-ANN 模型和年径流预报PCA-BP-ANN模型。

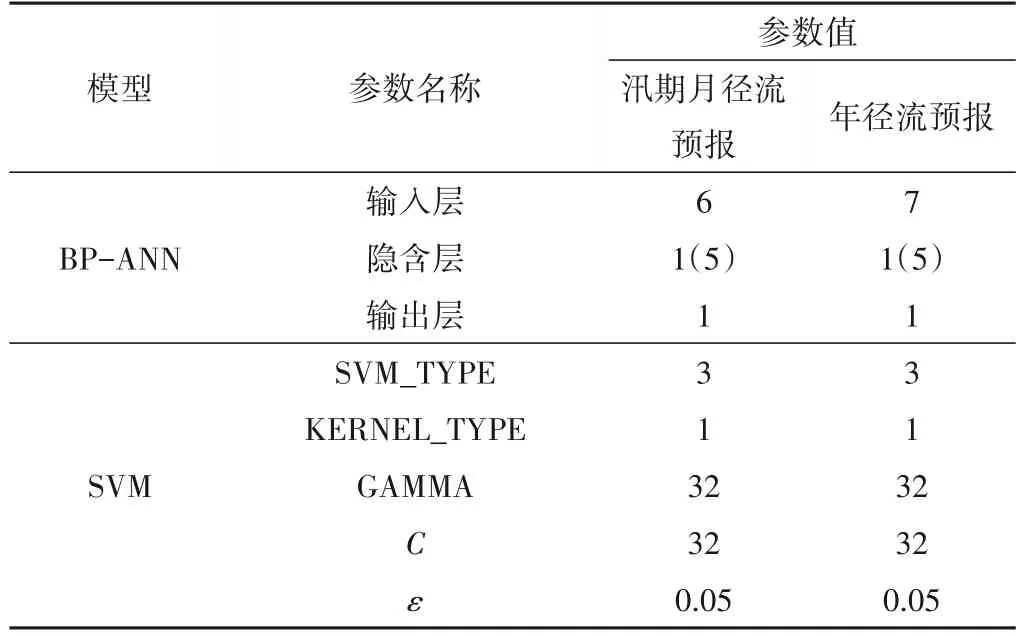
表6 BP-ANN和SVM模型参数Tab.6 The parameters of BP-ANN and SVM models

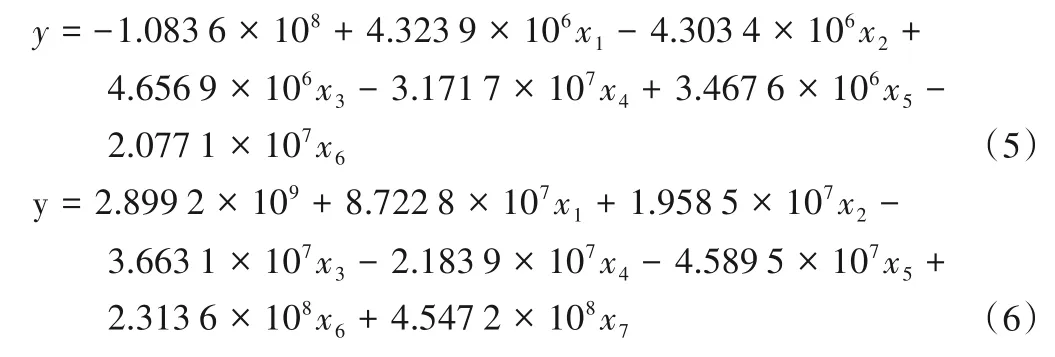
式（5）和式（6）中xi分别为该模型最终确定的月径流预报输入因子和年径流预报输入因子（见表4）。

图1给出了各月径流预报模型在率定期和验证期的模拟预报精度，由图可知，无论是在率定期还是在验证期，不同模型对不同月份的模拟预报精度均有一定差异。在率定期，TR模型在8、9 月份的模拟预报效果最好，合格率达90%，而在5、6、7 月份的表现却不如SVM模型；虽然SVM和BP-ANN机器学习模型的合格率在5、6 月份的合格率明显优于传统回归模型，但在8、9、10 月份却不如回归模型；结合主成分分析法的PCA-BP-ANN模型在6月份表现最差，但在7月和9月份的合格率要比没有采用PCA 方法的BP-ANN 模型高10%左右。在验证期，TR 模型在5月和10月份预报效果最差，预报合格率不足60%，而在7、8月份却能达85%以上，其中7 月份合格率达94%；PCA-BPANN模型虽在6、7月份预报合格率不足50%，但在5月份和8月份表现最佳，合格率均在85%以上，且该模型相对BP-ANN 模型精度提升了10%左右，说明结合主成分分析法（PCA）进行该流域月径流预报可有效提高汛期某些月份的预报精度。对比验证期和率定期，各模型在验证期的预报精度相对率定期均有所降低，而SVM 和BP-ANN 等机器学习模型在汛期各月表现相对稳定。

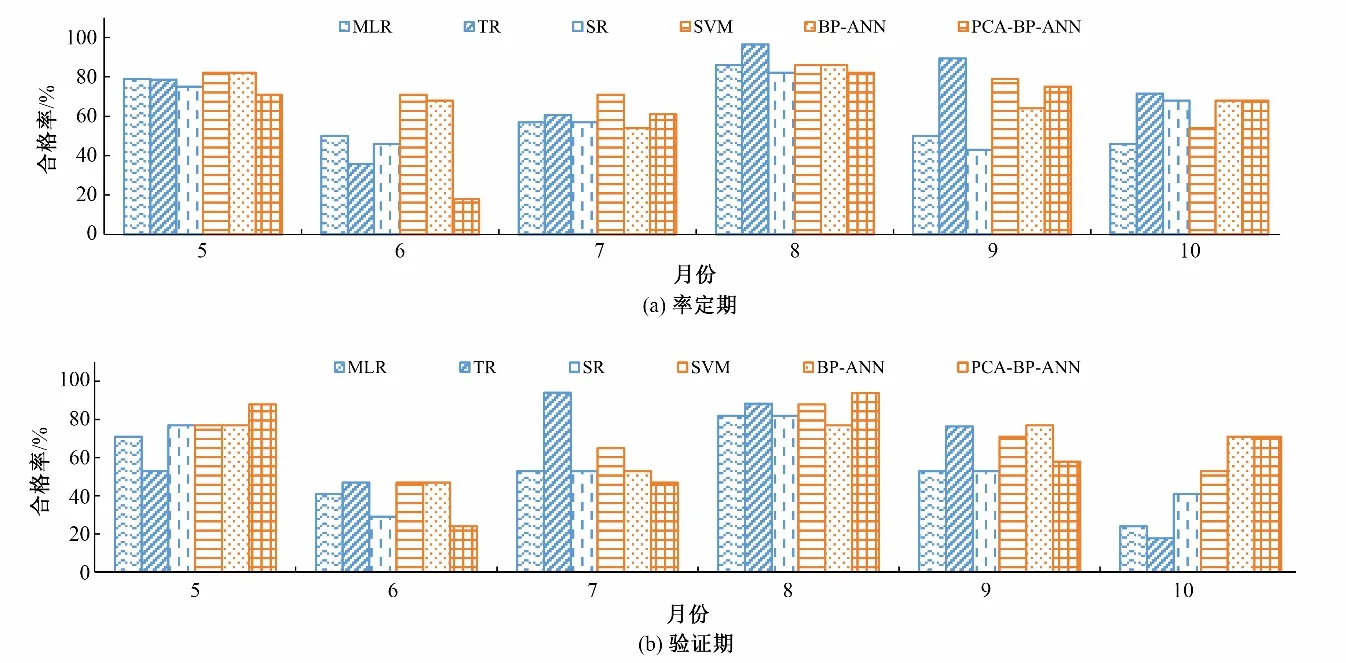
图1 汛期月预报各模型在率定期和验证期的模拟精度Fig.1 The simulation accuracy of monthly forecast models in flood season for both calibration and verification periods

由此可见，各模型均有“擅长”预报的月份，为充分发挥模型各自价值，实现多模型间的相互协调和性能互补，综合各模型的预报效果，表7 给出了汛期各月份推荐使用模型的最优预报方案。在预报各月来水时，采用该月份对应的推荐模型，除6月和10 月份，其他月份合格率均能在70%以上，并且在汛期来水最重要的7、8月份预报合格率能达90%以上。

表7 汛期各月份推荐使用模型Tab.7 Recommended model for each month in the flood season

从各模型在不同月份预报的整体效果来看，6 月预报效果较差，主要是受流域初始状态的影响，6月初流域内中小水库基本呈库空状态，同时该时段为流域灌溉期，因而该月径流受流域蓄水影响较大。7、8月份预报精度较高，是因为该流域在7、8月份降水量较大，径流量也大，从而受其他影响因素（包括流域初始状态、水利工程等因素）较小，允许误差大（见表1），因此预报合格率较高，预报效果较好。而9 月和10 月份预报精度较8月份降低，是因该流域于9月份开始降水逐渐减少，而上游众多水库会在9 月和10 月份蓄水截留导致预报水平降低。为进一步分析各月份预报效果的差异，计算汛期各月径流的变差系数（Cv）分析径流的不确定性，结果见图2，Cv值越大表示该月来水不确定性越大。由图2 知，5 月份Cv值最低，考虑是5 月径流大多由流域退水产生，来水相对稳定；而在6 月进入汛期后，径流受天然降水影响较大，不确定性较大，因此5月份预报效果优于6 月份；而10 月份Cv值最大，反应该月受降水和水利工程蓄水等影响导致来水不确定性最大，因而预报效果较差。

图2 汛期各月实测径流不确定性分析Fig.2 Uncertainty analysis of monthly measured runoff in flood season

图3为年径流预报各模型精度，对于年径流预报，各模型在率定期的预报合格率除了TR 模型外均达到90%以上，取得了较高的预报精度。验证期的预报精度有所下降，除了SR 模型外，其他模型预报合格率都在80%以上，但BP-ANN 和SVM 等机器学习模型预报精度明显高于传统的统计模型，其中SVM 模型的合格率为88%，BP-ANN 和PCA-BP-ANN 模型的合格率在90%以上，比统计模型高10%左右。此外，由于年径流预报的预见期较长，不确定性大，为了防止个别模型的预报误差较大而误导决策，推荐选用BP-ANN 和PCA-BP-ANN 模型，同时综合考虑其他模型的预报结果，最终确定合适的年径流预报结果。

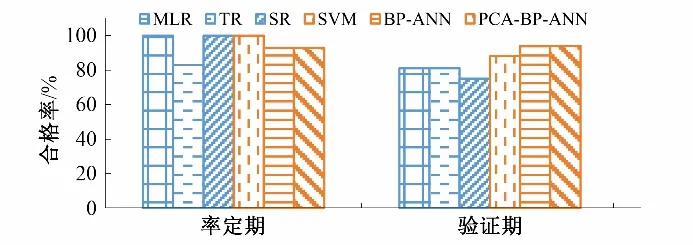
图3 年径流预报各模型在率定期和验证期的模拟精度Fig.3 The simulation accuracy of annual runoff forecast models for both calibration and verification periods

3 结论

耦合相关性分析方法和向前搜索包裹法确定桓仁流域汛期各月径流与年径流预报模型输入，并基于主成分分析重组因子以简化模型输入，综合考虑统计方法和机器学习方法，分别建立年径流预报模型和汛期月径流预报模型，对比分析各模型的预报水平，给出最佳预报方案，以提高桓仁流域长期径流预报的精度。主要结论如下：

（1）在月径流预报中，筛选出6 个关键影响因子，且上个月月降雨量起主要作用，其余6 个大气环流因子与预报对象的相关性和上月月降雨量水平相当，相关性系数均在0.5 以上；年径流预报中，筛选出7个关键影响因素，均为大气环流因子。

（2）基于多元线性回归（MLR）、多元门限回归（TR）、逐步回归（SR）、人工神经网络（BP-ANN）、支持向量机（SVM）和结合主成分分析的人工神经网络（PCA-BP-ANN）六种方法，构建了桓仁流域年径流预报模型和汛期月径流预报模型。对于年径流预报，BP-ANN、SVM 和PCA-BP-ANN 三个机器学习模型的预报效果优于传统统计模型，其合格率要比统计模型高10%左右；对于汛期月径流预报，各模型均有自己“擅长”预报的月份，利用最佳预报方案预报时，在汛期来水最重要的7、8 月份预报合格率均能达90%以上。

在进行流域长期径流预报时，考虑径流形成的物理基础和影响径流变化的各因素选择合适的预报因子，同时综合多种预报方法择优选择最佳预报方案，可有效降低流域长期径流预报的不确定性。此外，研究采用预见期为一个月，可满足多模型综合预报方法在该研究区有效性的论证，而该方法在不同预见期的有效性可能会有所区别，还需结合实际调度需求进一步检验，探索不同预见期下的最优预报方案，以更加合理地指导水库调度。