圆形断面明满流尾水系统水力过渡过程研究

林 杰，何相慧，杨桀彬，杨建东

（武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072）

0 引言

随着水利水电事业的发展，大量地下式水电站采用明满流尾水隧洞的布置方案。近年来西南地区的大江大河成为国内水电建设的主战场，河流洪水规模较大，洪、枯期尾水位变幅大，地下厂房普遍应用，明满流尾水洞逐步在二滩、彭水、向家坝、三峡右岸地下厂房等工程中得到应用，目前在建和已投入运行的水电站大部分都采用城门洞形断面。城门洞型断面具有施工方便、出渣运输条件好的优点，但其受力条件差，对地质条件有一定要求。而圆形断面相较于城门洞型断面，其结构受力条件好，可以有效适应更复杂地形［1，2］。

目前，对于水电站过渡过程的计算主要有模型实验、一维数值模拟和三维数值模拟三种方法。杨建东等［3］对水电站引水发电系统过渡过程进行了整体性模型试验，研究其大波动、小波动和水力干扰过渡过程，结果表明该试验能正确反映水轮机工作特性和管道系统水力特性，为水电站运行提供了参考的依据。周玉国［4］等采用模型试验和数值模拟两种方法对尾水洞明满混合流的流场进行了分析，揭示了尾水洞内气泡的生成机理以及洞顶的压力变化过程。孙洪亮等［5，6］通过物理模型试验对白鹤滩水电站尾水系统进行研究，分析了明满流产生的过程以及明满流段的优化措施等。陈刚［7］等针对尾水位变幅较大的水电站进行了物理模型试验研究，揭示了尾水系统在小波动工况下的动态特性。李高会等［8］运用虚拟狭缝法，对明流和有压流采用统一的明流方程组进行求解，分析了调压室对尾水隧洞明满流效应的缓解作用。张宗溥［9］等采用虚拟狭缝法将有压流方程与明流方程统一起来，用特征隐式格式法对模型进行计算，通过大量数值计算与水工模型试验结果进行对比，验证了该数学模型计算的准确性。付亮［10］根据水力特性的差异将尾水隧洞划分为有压满流区、明满流区和无压明流区，分别建立数学模型对带变顶高尾水隧洞水电机组的过渡过程进行研究，通过计算结果与实测数据的对比，验证了三区模型计算的可靠性。刘飞［11］等运用三维数值模拟的方法对尾水系统中非恒定流流态进行了模拟，通过与一维数值模拟和模型试验结果的对比，验证了三维计算的准确性，并对3种湍流模型进行了对比分析，结果表明RNG 和Realizablek-ε两种湍流模型对强旋流的适应性较好，精度能够满足工程实际要求。周俊杰等［12］采用CFD 方法对某尾水隧洞有、无通气系统两种体型进行数值模拟，分析了通气系统对尾水隧洞内明满流和洞顶负压的影响，对通气系统优化和布置具有重要意义。CAI F［13］等通过物理模型试验与CFD 数值模拟研究了调压室内立轴漩涡的产生机理，结果表明影响立轴漩涡产生的主要因素是淹没水深，可以通过降低速度环量和Fr（弗罗德数）的方法来抑制立轴漩涡的产生。安华［14］等，采用1D-3D 耦合方法对变顶高尾水隧洞明满流进行模拟并与传统的虚拟狭缝法结果进行比较，提出了虚拟狭缝法存在的缺陷。Zhou［15］等采用VOF方法，对含有气囊的管道系统进行模拟，发现在充水过程中，气液交界面的形态是不规则的。何相慧［16］等采用基于VOF 方法的三维计算和基于特征线法的一维计算对不同体型的调压室过渡过程进行模拟，分析对比了一维与三维计算的结果，验证了CFD 计算的可靠性，并揭示了T 型调压室中吸气漩涡的产生机理。

其中模型实验的研究方法比较直观、准确，但水电站工程体型大，且试验周期长、成本较高。一维数值模拟常用算法有激波拟合法［17］、刚性水柱法［18］和虚拟狭缝法［19-21］。其中虚拟狭缝法已被有效地用于工程实际中。三维数值模拟多相流的模型有VOF 模型、Mixture 模型和Eulerian 模型等，其中VOF 模型简单而有效，采用基于VOF 模型的三维数值模拟研究明满流的水流状态，已被证明与实际流态具有较好的吻合性，可为工程实际提供参考［22-25］。

为了研究圆形尾水隧洞明满流水力特性，本文以某水电站为计算模型，采用一维计算和三维计算相结合的研究方式，对该水电站城门洞形和圆形断面明满流尾水洞进行了大波动过渡过程数值计算，主要研究内容为调压室水位波动过程以及明满流分界面波动过程。重点分析大波动过渡过程工况下圆形断面明满流尾水洞水流流态，以期为相应的工程实践提供一定的参考。

1 计算理论

1.1 改进的虚拟狭缝法计算明满流

传统的虚拟狭缝法假设管道的顶部有一条非常窄的缝隙，满流可以看成为水面宽度很小的明流，有压非恒定流也可以用明渠非恒定流的基本方程进行计算。

明渠非恒定流基本方程如下：

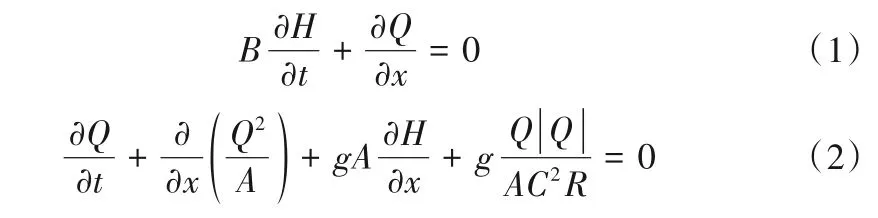
式中：x为沿渠长的水平距离；t为时间；H为水深；Q为水流流量；A为过水断面面积；B为水面宽度；R为水力半径；C为谢才系数；g为重力加速度，取值9.81 m∕s2。

但传统的虚拟狭缝法的假定与某些实际情况不符，该模型让流动系统各部分均与大气相通，认为只要水压低于管顶就是明流，水压高于管顶就是满流，而实际上有压管中即使压力为负也不一定变为明流，如果有大气泡存在，即使压力高于管顶，气泡下明流也不会变成满流，因此在涉及负压、气泡以及液柱分离时就无法较好的模拟明满流态。

明满流尾水系统水力过渡过程的特点是：在同一时刻洞内既存在明流段，又存在负压段。为了克服上述的缺陷，在计算过程中通过不断地跟踪明满流的分界面，区分满流区和明流区，明流区的水深由压力决定且总是低于管顶；满流区的水深与压力无关，计算中令水深总高于管顶。这样，当满流区产生负压时也可以用虚拟狭缝法计算［26］。

1.2 Realizable k-ε模型

标准的k-ε模型［27］在假定时认为μ1是各向同性的标量，因此该模型在模拟强旋流、弯曲流线流动等问题时，往往会产生一定的失真［28］。Realizablek-ε模型将湍动黏度计算式与应变率联系起来［29］，能够有效模拟旋转均匀剪切流、管道内流动等问 题。在Realizablek-ε模型中，关于k和ε的输运方程如下［29，30］：

式中：ρ为流体密度，g∕cm3；k、ε分别为湍动能和湍动耗散率；Gk是平均速度梯度引起的湍动能k的产生项；μt为湍动黏度，Pa·s；u为平均速度，m∕s；σk和σε分别是与k和ε对应的Prandtl 数；Cμ为经验常数；υ为运动黏度，m2∕s；C2为模型系数。

1.3 VOF气-液二相流模型

VOF 的基本原理是通过网格单元中流体的体积与网格体积比函数F 来确定自由面，追踪流体的变化而非自由液面上质点的运动。该模型适用于求解两种或三种不能混合的流体，通过求解单独的动量方程和处理穿过区域的每一流体的容积比来模拟流动［31］。

2 计算模型

2.1 断面形状

采用某圆形断面尾水洞水电站为研究对象，为了更好的说明圆形断面尾水洞水电站明满流水力特性，设计了城门洞型尾水洞进行对比，断面尺寸如图1 所示。二者断面面积和洞高相同，且城门洞断面顶部圆弧段半径与圆形断面相同，当两断面为满流时，城门洞断面湿周χ1=61.91 m，圆形断面湿周χ2=57.49 m。即与圆形断面相比，城门洞型断面在拱顶以上与圆形断面面积相同、圆弧半径相同、湿周相同，拱顶以下，面积相同，湿周不同。

图1 断面尺寸（单位：m）Fig.1 Section size

2.2 模型边界条件

本文的一维计算采用Topsys进行建模计算。Topsys计算程序为武汉大学开发的水电站过渡过程计算软件，该软件已应用于国内多座水电站的开发工作，经过与模型试验和电站实测数据的对比，Topsys计算得到的调保参数精度高，结果可靠［32］。

本文的三维计算采用Solidworks 进行建模，模型水电站为两机一洞布置，计算区域从水轮机尾水管出口到下游尾水洞出口，计算模型如图2（a）、（c）所示。

本文的计算工况选取明满流典型工况D11：下游一台机发电水位1 130.35 m，额定水头80 m，同一水力单元下一台机组停机，另一台机组额定出力运行时甩全部负荷。机组导叶关闭规律如图2（d）所示。

尾水管出口设置为质量流量进口（inlet1、inlet2），给定由一维程序Topsys 得到的机组流量变化过程，在恒定流状态下给定为机组的引用流量，在非恒定流状态下给定一维计算得到的每个时间步的流量。调压室顶部及下游水库顶部设置为压力出口，给定压力值为0 atm。水库的侧面（outlet）设置为压力出口，按照所计算的工况通过场函数给定压力边界。

2.3 网格划分和监测点、面

网格划分采用Star-CCM+自带的六面体网格。网格基础尺寸设置为0.8 m，调压室部分加密为0.4 m，圆弧过渡位置，局部特征尺寸较小的位置均采用自动加密，圆形断面尾水洞明满流系统网格总数约66.44 万，城门洞型尾水洞明满流系统网格总数约65.63 万。经过网格无关性分析，该网格数满足计算要求。

三维计算监测点、面布置如图2（b）所示为了监测调压室涌浪波动，在调压室底板取监测面，监测其相对压强Pu（Static Pressure）。在调压室下方岔管处取监测面，监测其相对压强Pd，调压室水位表达式为Z=P∕9 810+Z0，其中，Z0为调压室底板高程。在阻抗孔处取监测面，监测其截面流量总和变化。为了跟踪明满流界面，不同工况在明满流界面可能经过的地方布置洞顶监测线，监测其第二相的体积分数（volume fraction of phase 2），即VOF多相流模型中的水的体积分数α。

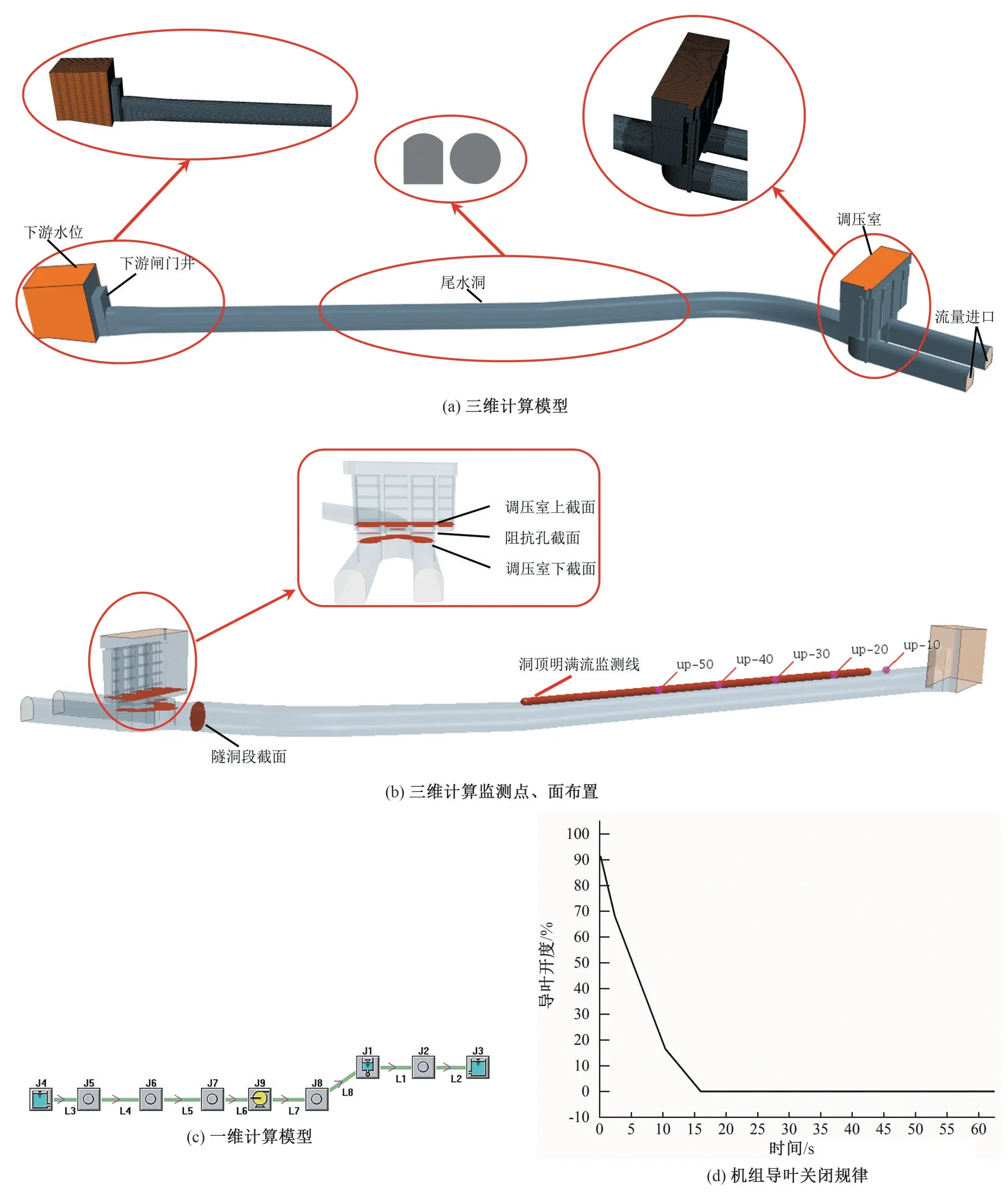
图2 计算模型Fig.2 Calculation model

2.4 计算方法

本文的三维计算借助于商用CFD 软件STAR-CCM+，离散方式采用有限体积法对控制方程进行离散，湍流模型选用Real‐izablek-ε模型，固体壁面为无滑移壁面，近壁区低Re流动采用壁面函数法进行处理，运用VOF 模型处理水气交界面。三维恒定流计算需要较长时间才能收敛，因此，在大波动过渡过程之前，给定一维恒定流的边界条件进行恒定流计算。恒定流计算结束后，以一维计算的流量变化为进口边界条件，进行大波动过渡过程计算。

3 结果与分析

3.1 不同断面计算结果对比分析

两种不同断面尾水洞调压室涌浪极值结果如表1所示。由表可知，一维计算的圆形和城门洞形断面尾水洞的调压室初始水位分别为1 131.09 m 和1 131.07 m，差值为0.02 m；调压室最高涌浪分别为1 133.88 m 和1 134.02 m，差值为0.14 m，发生时间相差0.7 s；最低涌浪分别为1 124.80 m 和1 124.82 m，差值为0.02 m，发生时间差0.15 s；涌浪周期均为114.0 s。三维计算的调压室涌浪初始值差值为0.01 m，调压室最高涌浪、最低涌浪和周期均相同。调压室涌浪波动的微小差异是由于圆形断面与城门洞断面在保证面积、高度一样的前提下，湿周不同而造成的。图3、4 是调压室涌浪波动的变化过程，可以看出一维计算和三维计算下的两种断面的调压室涌浪波动过程吻合度都较高。

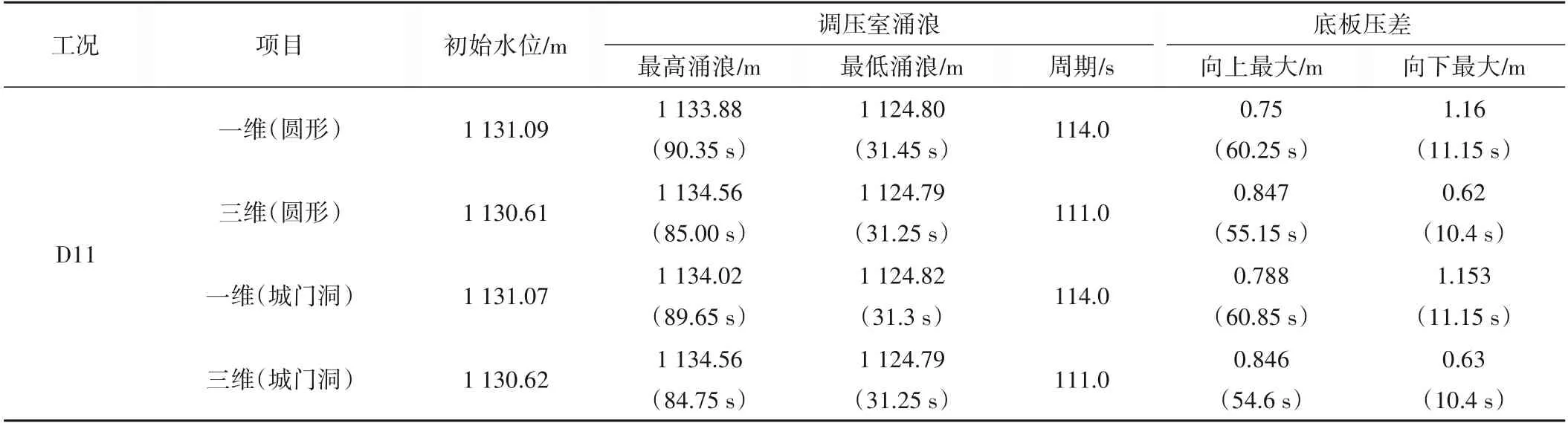
表1 调压室涌浪水位极值Tab.1 Surge water level extreme value of surge tank

图3 调压室涌浪变化过程（1D）Fig.3 Surge change process diagram of surge tank（1D）

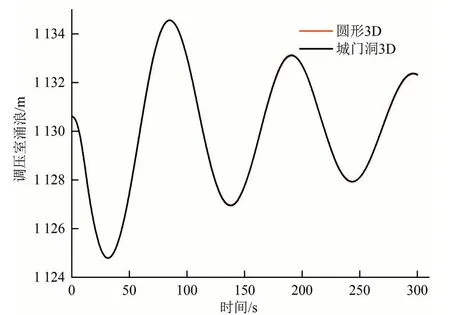
图4 调压室涌浪变化过程（3D）Fig.4 Surge change process diagram of surge tank（3D）

图5、6为一维计算和三维计算的两种断面尾水洞明满流分界面的移动过程，由图5可知，一维计算的圆形和城门洞形尾水洞洞的明满流分界面的移动规律一致，明满流交界面初始位置（距下游出口）分别为104.29 m 和104.31 m，差值为0.02 m；极大值处位置分别为151.20 m 和150.90 m，差值为0.70 m；极小值位置分别为88.31 m 和88.00 m，差值为0.31 m。三维计算的分界面初始位置相同，均为101.98 m；极大值位置分别为142.98 m和143.18 m 差值为0.2 m；极小值位置分别为75 m 和75.4 m，差值为0.4 m。在壅水波转换为退水波时，两种断面均产生了较短时间的左右波动，相较于城门洞断面，圆形断面在壅水波传递后时间段略快于城门洞断面，在76 s 到达第一次波谷，城门洞为77.75 s，随后两断面均产生相同规律的小幅波动，波动幅值分别为13.75 m（圆）和14.05 m（城门洞），波动周期分别为13.75 s和14.05 s。可以看出，一维计算的两种断面的明满流分界面移动过程差别较小。

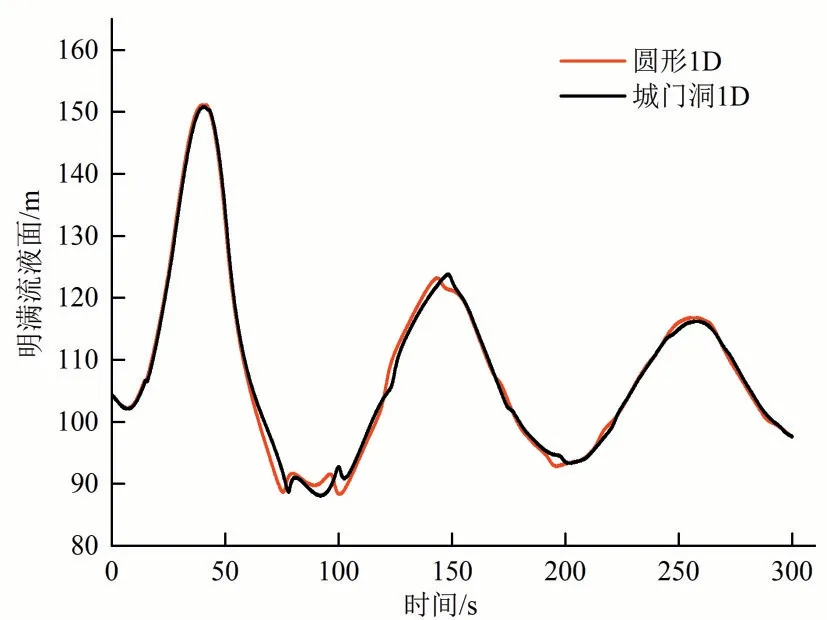
图5 不同断面明满流分界面三维计算结果对比（1D）Fig.5 Free surface-pressurized flow interface of different sections（1D）

图6为三维计算的城门洞形和圆形断面尾水隧洞明满流分界面随时间移动过程，两种断面下的明满流分界面的极限位置基本一致，液面移动规律大致相同，在明满流液面向下游传播的过程中，圆形断面的明满流分界面移动速度相比于城门洞断面要慢一些，其在达到最右侧后的波动时间也略小于城门洞断面。

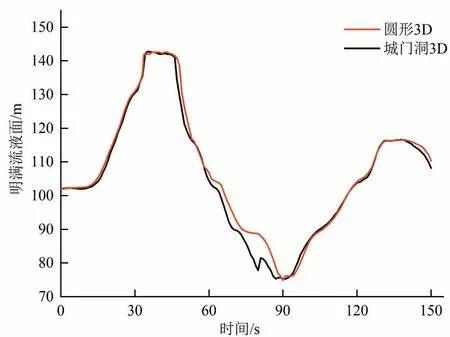
图6 不同断面明满流分界面三维计算结果对比（3D）Fig.6 Free surface-pressurized flow interface of different sections（3D）

综上，当城门洞型尾水断面和圆形尾水断面过流面积、洞高及洞顶圆弧半径相同时，两种断面形状下的调压室涌浪过程和明满流分界面的移动规律基本吻合。因此，两种断面在水力特性方面，并无明显差异。

3.2 明满流交界面移动及洞顶气囊

经过对比分析，圆形断面和城门洞形断面在大波动过渡过程明满流分界面移动过程中，二者波动规律一致，下面以圆形断面尾水隧洞为对象，重点分析其大波动过渡过程明满流交界面移动及洞顶气囊变化。

在进行过渡过程计算时，为了得到稳定的流场，首先进行了1 000 s的恒定流计算，在900 s时调压室液面为1 130.614 m，随后100 s 液面波动的相对幅值（幅值∕调压室水深）为0.02%，流场达到稳定。图7为过渡过程典型时刻调压室及圆形尾水隧洞液面位置图。初始时刻［图7（a）］，此时液面由于壁面黏附力的作用，与坡顶存在一定的交角。机组开始甩负荷时，水轮机流量减小，下游调压室向尾水洞补充水量，其水位下降，明满流交界面及水面以退水波向上游传播，水面线呈上凹型，甩负荷11.25 s 时流出调压室的流量达到最大值［图7（b）］。随着调压室涌浪水位的降低，尾水洞中水流部分开始转向，甩负荷31.25 s时［图7（c）］，调压室达到最低涌浪，尾水洞中反向水流作为主导，随后尾水洞向调压室补充水量，水位上升，此时明满流分界面由于水流惯性的作用继续向前推进，移动速度变缓。

图7 典型时刻液面位置图Fig.7 Liquid level position map at typical moments

甩负荷33.50 s 时［图7（d）］，水面停止向前推进，退水过程转化为平槽管线增容过程，水面线呈直线。洞顶气体在增容作用之下，继续向上游方向扩散。甩负荷44.00 s 时［图7（e）］，平槽过程结束，明满流分界面达到最左侧（142.98 m），随后水面开始向下游推进，在壁面及表面张力的作用下，部分水体黏附在壁面，壅水波水面线呈上凹型［图7（f）］，推进过程中，受水流影响，尾水洞顶部气体继续向上游扩散，进一步发展。甩负荷55.00 s 时［图7（g）］，部分洞顶气囊破碎。甩负荷74 s 时［图7（h）］，气囊不再向上游扩散，随着明满流界面继续向下游推进，洞顶气囊逐渐消散、溃灭。甩负荷85.00 s 时，调压室涌浪达到最高水位，随后尾水洞中正向水流作为主导，明满流分界面继续向下游推进，在甩负荷90 s 时［图7（i）］达到最右侧（75.00 m），水面线呈上凹曲线［图7（j）］，壅水波转变为退水波，随后洞顶气囊迅速溃灭、消散，在洞顶产生负压。波动三个周期后，明满流分界面移动时已不再产生气囊。

3.3 洞顶监测点监测结果对比分析

大波动工况下，明满流分界面移动过程中，伴随着洞顶气囊的产生、发展、破碎与溃灭，且至少持续3 个周期。由图7 可知，洞顶气囊的破碎与溃灭过程较为缓慢，且在甩负荷84s时扩散到最左侧，随后逐渐破碎溃灭，未对机组产生影响。

为了进一步分析洞顶气囊溃灭时对管道壁面的冲击，以及明满流尾水洞负压的大小，对明满流波动范围内两种断面的洞顶压力进行了监测，监测点布置见图2（b），洞顶压强水头表达式为P（H2O）=P∕9 810，单位mH2O。计算结果见图8。监测点up-24～up-28 为明满流波动区的典型测点，由图8 可知，两种断面在相同监测点处的洞顶压力波动过程一致，极值差值较小，且在监测点up-24～up-28 的负压水头均较小，最大负压为不超过0.4 m，均发生在up-26 监测点。另外，up-24～up-28 测点的压力水头波动曲线未出现阶跃值，因此洞顶气囊破灭时，未对壁面产生明显的冲击压力。

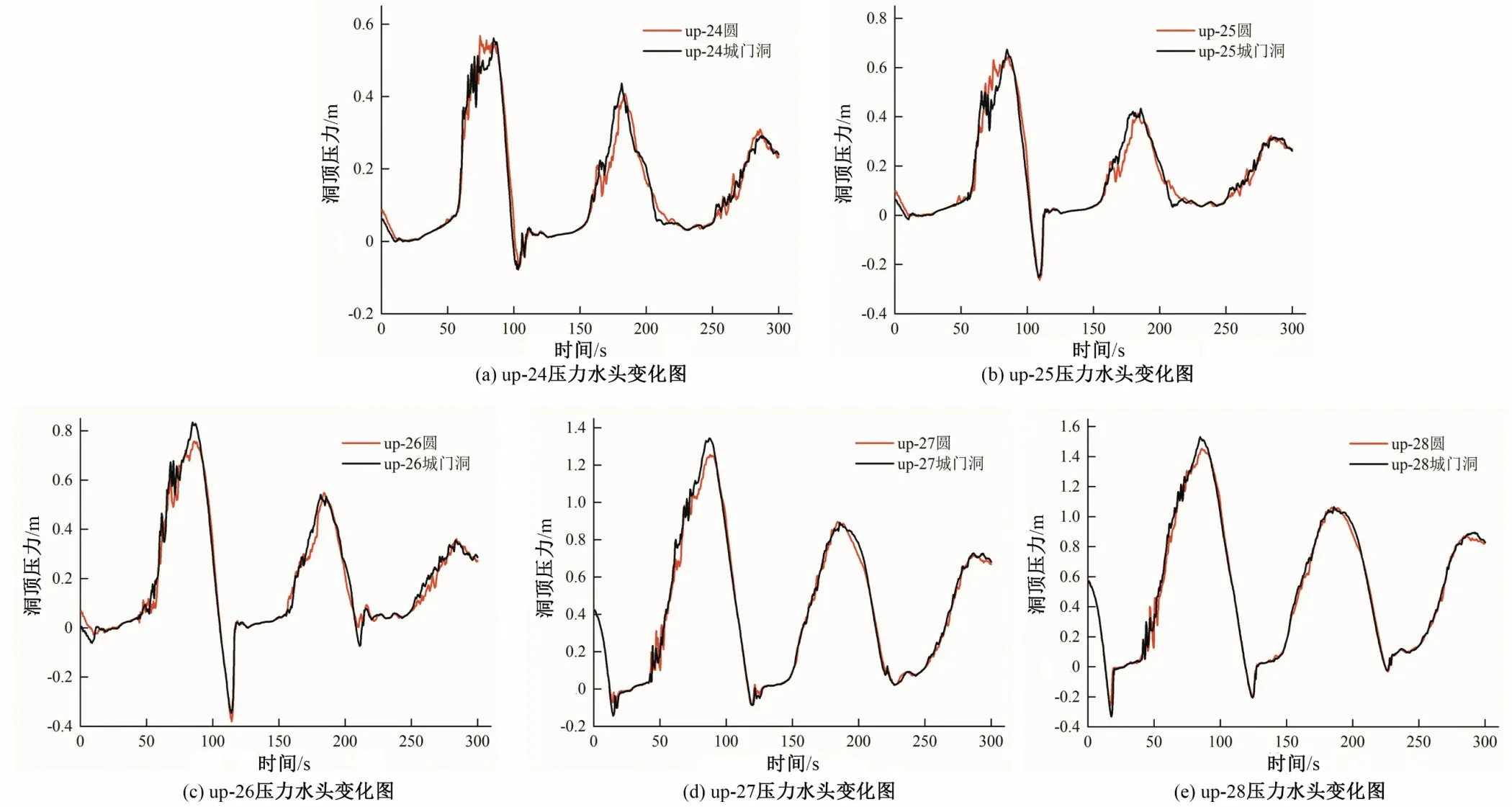
图8 洞顶监测点up-24～28压力水头变化图Fig.8 The pressure variation process at the monitoring point up-24～28

3.4 一维和三维计算结果对比分析

在控制断面面积、高度和洞顶弧度相同的条件下，圆形与城门洞形断面的调压室涌浪波动和明满流分界面移动吻合度较高，下面重点分析圆形断面尾水洞一维与三维计算差异。

图9 为一维计算与三维计算的对比图。结合表1 数据可知，一维与三维计算的最高涌浪与最低涌浪的差值分别为0.68 m 和0.01 m（相对误差δ分别为6.9%和0.1%），周期的差值为3 s（δ=2.7%），吻合度较高。一维与三维的初始水位差值为0.48 m（δ=4.9%），是由于三维计算的管道糙率与一维计算有所差异，导致沿程损失不同造成的。由图9（a）～（b）可以看出，一维和三维计算的调压室涌浪波动和进出调压室的流量规律相同，均随时间周期性递减。图9（c）为圆形尾水隧洞明满流分界面随时间移动过程，其三维计算和一维计算液面移动规律相同，周期相近。恒定流时，一维与三维明满流液面位置分别为104.29 m和101.98 m，差值为2.31 m。明满流界面波动时，一维与三维计算退水波的极限位置分别为151.19 m（42 s）和142.98 m（44 s），壅水波的极限位置分别为88.31 m（100.9 s）和75.00 m（90 s），这是由于一维计算将明满流液面的波动过程进行了简化，而实际流动中，明满流分界面移动过程的壅水波和退水波的形态各不相同，后续将结合三维计算捕捉到的液面位置变化及速度变化图进行进一步分析。

图9 一维与三维计算对比图Fig.9 Comparison of 1Dl and 3D calculation

3.5 明满流液面波动形式分析

图9（c）为尾水隧洞明满流分界面随时间移动过程，三维计算通过明满流监测线进行监测，三维计算和一维计算液面移动规律大致相同，但两者之间存在差异，这是由于一维与三维水头损失的不同、三维计算液体表面张力的影响以及一维与三维计算水深时的算法不同，导致模拟明满流分界面移动范围和明满流水面线形态的差异。为了对一维和三维计算的明满流分界面运动形式进行进一步分析，绘制典型时刻的分界面如图10所示。初始时刻［图10（a）］，由于三维计算沿程水头损失较小，其水面线低于一维计算的水面线，但是由于液体表面张力的作用，三维计算的分界面与圆形尾水洞存在接触角，导致其初始位置相差2.31 m。

一维计算在模拟明满流液面时，忽略了壁面黏附力的作用，水面呈直线传播，而三维计算则考虑了表面张力以及壁面黏附力的作用，明满流液面在退水波和壅水波传播过程中水面线呈现上凹曲线，在一定的程度上减缓了水面线向上（下）游的快速传播。由图9（c）知，在甩负荷34 s 时，三维计算的分界面呈现较小的左右波动，持续10 s，该过程反映了退水之后的平槽过程，而一维计算的水面仍以直线向上游传播，在达到极限位置后发生转向，向下游传播。平槽过程结束后三维计算水面线恢复上凹型曲线［图7（f）］，分界面开始以壅水波向下游传播，此时明满流分界面达到极大值位置［图10（b）］。因此一维计算的水面线更靠近上游侧。

图10 一维与三维计算明满流分界面极值位置示意图（单位：m）Fig.10 Diagram of one-dimensional and three-dimensional calculation of the extreme value position of the free surface-pressurized flow interface

明满流分界面到达最右侧时［图10（c）］，由图9（c）可知一维计算的明满流分界面产生了幅值较小的左右波动，此时三维计算的明满流分界面由于水流惯性继续向右侧以壅水波推进，水面线呈上凹曲线［图7（j）］，因此三维计算的明满流分界面更靠近右侧，二者差值为13.31 m。一维计算和三维计算的明满流波动范围相差5.1 m。另外，三维计算的VOF 液面捕捉法与一维计算的简化的三区模型动网格算法存在一定的差异，也会导致明满流分界面移动范围的差异。

4 结论

本文对某圆形断面尾水隧洞水电站模型进行了一维和三维计算，分析了大波动过渡过程下的调压室涌浪和明满流波动情况，并与城门洞型尾水隧洞计算结果进行了对比分析，主要结论如下。

（1）当城门洞型尾水断面和圆形尾水断面过流面积及洞顶圆弧半径相同时，两种断面形状下的调压室涌浪过程、进出调压室流量规律和明满流分界面的移动规律基本吻合。因此，两种断面在水力特性方面，并无明显差异。

（2）两种断面的明满流波动过程均包含退水、平水、壅水三个过程。三维计算的水面线在平水过程呈现小幅的上下波动，而一维计算水面线仍向上游继续传播，因此三维计算的明满流波动极大值位置更靠近下游侧。当壅水波向下游波动到极限位置时，仍呈现壅水波形态，因此三维计算的明满流波动极小值位置更靠近下游侧。

（3）Topsys 能够较好的模拟调压室涌浪波动过程和尾水洞明满流液面的移动过程，由于计算方法的不同，与三维计算存在一定差异，但差异较小，在一定程度上可以满足计算精度要求，可以应用于工程实践。

（4）明满流工况下，尾水洞退水波速度较大时，洞顶出现残留气囊，但洞顶气囊会随水流波动融合、溃灭，且气囊破灭产生的冲击压力较小，不会对尾水洞结构产生破坏。

（5）综上，圆形断面明满流尾水洞流态是合理的，与常见的城门洞形断面明满流尾水洞并无明显的差异。说明明满流尾水洞采用圆形断面设计在水力学方面可行的，合理的。