基于运营难度系数的水电站标准化运营管理评价研究
金 艳,闫孟婷,罗立军,肖 杨,何葵东,黄炜斌
(1.国家电投集团水电产业创新中心,湖南长沙 410004;2.四川大学水利水电学院,四川成都 610065)
0 引言
2021 年3 月15 日,习近平总书记主持召开中央财经委员会第九次会议,强调把碳达峰碳中和纳入生态文明建设整体布局。碳达峰碳中和的本质是以能源转型为基础、以电力转型为核心、以新电气化为引领的生产方式和生活方式的深刻变革[1]。在能源结构转型持续升级的背景下,中国可再生能源持续快速发展,截至2020 年底,我国常规水电装机达到3.38 亿kW,年发电量135 万GWh,在建规模约4 800 万kW[2]。目前,常规水电技术开发程度超过55%,虽还蕴藏较大开发潜力,但在多重因素的限制下,未来水电开发增速将会放缓,在此情况下,重视已建成工程的后期工作,注重水电运行成本效益,将有利于实现存量水电的精细化管理,促进水电可持续发展[3]。不仅如此,对于企业而言,开展聚焦成本效益的水电标准化运营管理评价既有利于挖掘潜在可节省成本,同时有利于企业发现薄弱环节,提升企业综合管理能力。
由于水电站个性化差异较强,电站间横向评价比较困难,因此本文重点探索了水电站复杂个性在考核管理中的合理表达—定义了水电运营难度系数,选择六十余座水电站为研究对象,从水电不同重要程度特征属性的提取、水电站运营难度系数模型构建、综合评价等发面开展了相关研究。
1 水电站运营难度系数
目前水电企业成本对标评价指标多采用各项成本值与装机容量的比值,如单位千瓦修理费、单位千瓦人工费等,即利用装机容量使各个电站具有统一的可比基础。但实际运营中可以发现,装机容量相同的电站由于具有不同的坝面积、闸门面积、机组类型等,仍会导致其成本投入方面有不同的表现。更大的闸门面积意味着更多的防腐费用,更复杂的机组类型意味着更高额的维护费用等。如何量化不同电站间的差异性,从而使电站具有更合理、更符合实际的比较基础是本研究的重点,为进一步探索水电差异性表达,本文提出了水电站运营难度系数概念。
1.1 水电站运营难度系数概念
运营难度系数是一个较为抽象的概念,与电站机组规格、地理位置、智能化程度等息息相关,但无论运营难度系数如何抽象,电站本身的成本支出是可量化的,故对水电站运营难度系数的研究可转化为对水电站成本的研究。
水电企业在经营期内,所有成本都围绕电力生产直接或间接发生,主要包括职工薪酬、折旧费、材料费、检修维护费、水费、税费、财务费用和其他费用。按照成本是否能通过电站运营水平、管理技术变化而改变为依据,重新对成本进行划分,将无法反映电站运营水平且多依赖于政策如税收金、折旧费等成本称为硬性成本,其余称为软性成本;总成本扣除硬性成本则可得到软性成本,也称为运营成本,这一部分成本属于水电企业可控制成本,可用于衡量水电站运营难度系数[4,5]。
基于运营成本的水电站运营难度系数计算方法见式(1)。
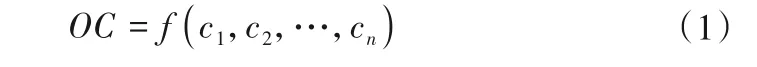
式中:OC为Operational Complexity 即水电站的运营难度系数;cn为运营成本中的第n个分项;f为运营难度系数与成本之间的关系函数。
需要说明的是,运营难度系数并非独立的评价指标,其本身也并不具备好坏之分,反映了电站日常运营中无法通过主观能动性改变的客观条件,是用于改进传统评价指标无法横向评价的关键参数。
1.2 运营难度系数影响因素分析
本研究围绕水电运营难度系数,引入全面质量管理(Total Quality Management,TQM)中关于“人、机、料、法、环”相关概念[6],对水电站运营成本进行解构(如图1),解构后的运营成本与水电常规成本分类最大不同在于分类逻辑的区别,并提出了技术成本二级分项,同时考虑外部环境对水电站成本的影响。
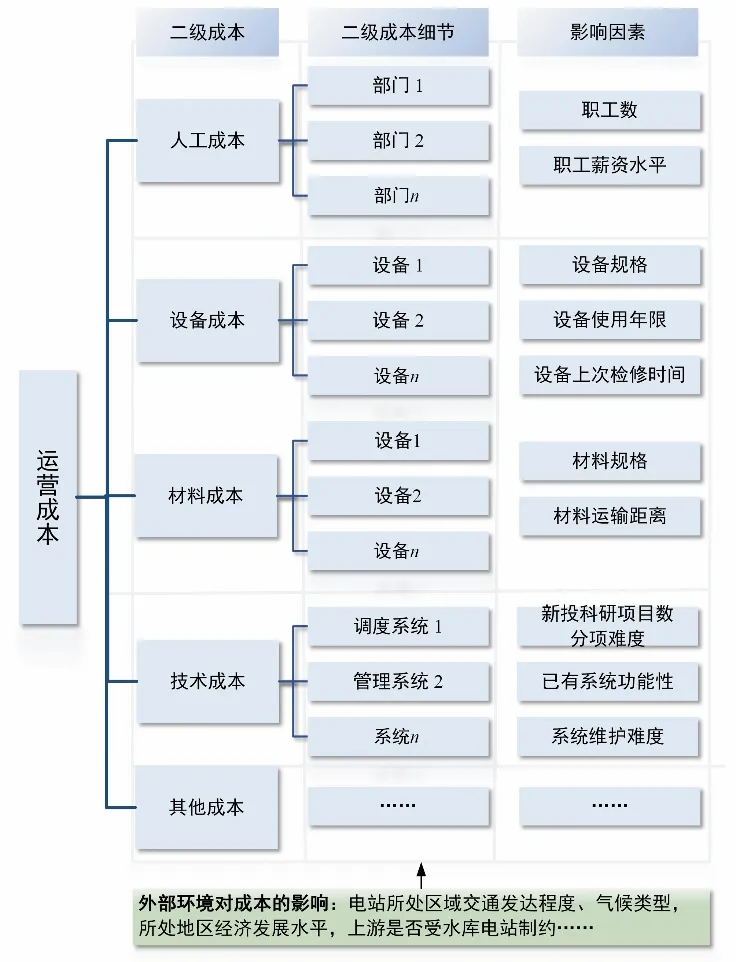
图1 基于全面质量管理的运营成本解构示意图Fig.1 Schematic diagram of operating cost solution based on comprehensive quality management
2 基于随机森林的运营难度系数模型构建
随机森林回归是基于分类回归树的一种集成学习方法,利用bootstrap有放回的从原始数据集中抽取多个大小相同的随机样本,同时在构建单个决策树时随机抽取特征子集,“森林”利用决策树对每个抽取的随机样本进行建模,最终结果由所有决策树投票得出[7]。
2.1 基于Gini指数的重要特征分析
在对水电站运营情况的分析过程中,研究者总希望尽可能多的收集有关影响因素,从而进行全面完整的评价。然而收集到的个影响因子之间往往具有相关性,涵盖的信息存在交叉、重叠情况,使问题复杂化[8]。重要特征分析则是在众多影响因素中识别出影响程度最大的因素,解决上述问题。
假设有M个特征的原始数据的输出变量类别为k,基于Gini 指数(GI)来量化各特征(指标)的重要性得分(Importance Mark,IM)流程为[9]
(1)计算Gini指数。

式中:nt为决策树数量。
通过重要特征辨识结果,可以提取出不同重要程度的影响因素,根据其与运营难度系数内在关联情况,利用随机森林建立运营难度系数模型,为标准化评价的实现奠定基础。
2.2 方法概述
提取出主要影响因素后,随机森林回归计算步骤可以概括如下:
(1)形成决策树训练集:若原始数据集含n个样本,随机有放回地抽取n个训练样本形成抽样数据集,用于形成决策树。
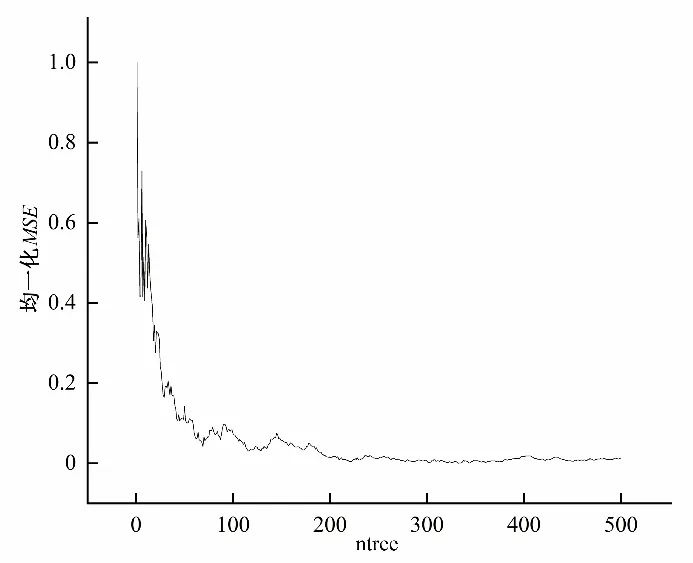
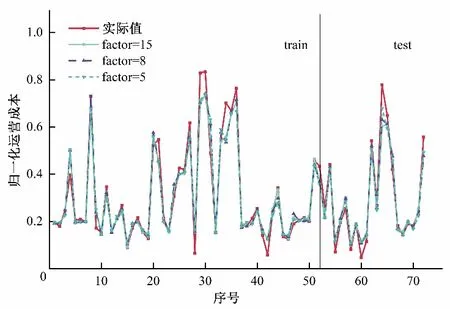
(2)随机选择决策树特征:若原始数据样本特征维度的M,从中随机m个特征(m (3)组成随机森林:重复步骤(2)、(3)形成多个决策树构成森林,树的数量ntree由具体的情况决定。 (4)结果输出:针对回归分析,其最终结果如式(6),表示回归结果为单个树结果的平均。 结合可拓论、物元分析理论、关联度理论确定经典域物元、节域物元、待评物元以及关联数,引入熵权法计算指标的综合权重以避免指标权重的绝对主观性和绝对客观性[11],建立水电站标准化运营管理综合评价方法。方法将多目标评价转换为单目标决策问题,最终达到定量分析的目的[12]。 将物元定义为一个有序三元组R: 式中:N为事物名称;C为事物的特征;V为特征的量值。 N、C、V三者构成了物元三要素,如果事物N用n个特征{c1,c2,…,cn}以及相应的量值{v1,v2,…,vn}来描述,则称R为n维物元: 可拓学评价方法是对研究对象从可行性和优化(满意程度)的角度来进行评估的,实质上是一种多属性决策分析方法。它利用可拓集合的基本理论和物元的可拓性定性分析,通过关联函数进行定量计算。该方法可以将各个评价指标的关系转化为一种相容的问题,通过距离函数对点和区间之间的距离进行度量[13,14]。 为了了解数据的客观信息,研究选择熵权法确立指标权重。熵权法的核心是信息熵,用于解决信息量化问题[15]。信息熵反映在属性值上理解为属性值变异程度的大小,属性值的信息熵越大,它的变异程度越大,可获取的信息量越小,其在决策中所起到的作用也越小[16]。 采用基于信息熵的决策方法确定各指标权重系数,计算方法为: (1)由于各指标的量纲不同,需对各指标数据进行标准化处理。构建m个评价指标,n个评价单元(水电站)的评价对象原始矩阵X=(xij)mn,对其进行标准化处理得到 (3)计算指标i的信息熵。 (4)计算指标i的权重。 3.3.1 关联度函数 关联度函数基于模糊综合评价中的隶属度函数拓展了点到区间的距离,提出距的定义,待评价物元中第i个指标xi对于评价等级o的关联度为Ko(xi),关联度函数形式多样,需要根据指标具体情况具体分析,从而选择适合某项指标特性的关联度函数[19],研究采用以区间端点为最优关联,计算见式(18)。 式中:ρ(xi,x0,Xo)为侧距,该距在点x0处达到最大值。 此种关联函数可以根据x0的取值,在区间任意点取得最大值,若x0取在端点aoti或boti,此时关联函数则在两端取得最大值。 3.3.2 综合评分 传统地,通过电站j的第i项指标关于等级o的加权关联度,结合最优隶属度准则可得到不同电站的隶属等级[20],如式(19)所示。 式中:Gij(o)为电站j的关于等级o的加权关联度;其值为该电站各指标关于等级o的关联度与权重乘积之和;Gj为电站j最终等级,其由电站最大关联度所对应的等级确定。 式(20)是可拓学中最常用的评分确定方法,其最终评价结果与设定等级一致,通常为带次序的分类值或离散型数值,然而本研究中希望得到更为精确的得分值,以供对标管理分析使用,故按照研究目标对综合评分方法进行改进。 式中:Gj(i)为电站j关于指标i的最大关联度所属等级;adj.Gj为电站j改进综合等级得分,由该电站单项指标等级加权求和得到。 选择某省65家水电站作为研究对象,数据均进行了归一化处理。首先按照7:3的比例将数据集分为训练集、测试集,在重要特征筛选过程中,将影响水电站运营难度系数的因子称作解释变量,运营成本数据序列作为因变量,对于水电站集H={H1,H2,…,Hk},按照研究目的,将影响因素分为机组特性、坝型特征、水位特征、库容特征、劳动力特征、调节性能,每类特性用至少1 个因子进行描述,形成电站影响因素数据集Xi={X1,X2,…,Xp},根据现有资料,设定15 个因子(p=15),X1~X15分别是装机容量、机组台数、正常水位、死水位、总库容、有效库容、坝高、坝长、职工人数、平均单机容量、水位差、平均机组利用小时数、投产时长、坝面积、调节性能。 随机森林参数包括决策树选择进行分裂的特征数m,以及树的数量nt。对于回归分析,每颗决策树通常随机选择m=M∕3个特征进行分裂,本研究原始特征维度(自变量)为15,故令m=5;nt则通过固定m进行搜寻,认为均方误差(Mean Squared Error,简称MSE)最小时nt取得最优值。 首先,将训练集中所有变量均作为输入,得到不同nt值与其对应MSE,如图2 所示。由图2 可知,当决策树数量达到200时,误差趋于平稳,MSE在nt为332 时取得最小值,故在本次计算分析中设定nt=332。 图2 不同决策树数量及其对应MSEFig.2 Different decision trees and their corresponding MSE 计算不同影响因素的重要程度,并对结果降序排列,随机森林方法求解得排序前八项的重要特征分别为装机容量、平均单机容量、职工人数、坝长、坝面积、有效库容、总库容、机组台数。 基于上述分析,分别提取经随机森林筛选出的前5、前8 项重要特征再次进行随机森林回归分析,此时nt最优取值分别为324、102,随机森林3次拟合结果如图3所示。 图3 随机森林拟合结果Fig.3 Random forest fit results 观察图3、3 次随机森林回归结果非常类似,最大的区别在于测试集中的64 号电站,特征数量为5 的随机森林拟合值更贴近实际值。定义合格率为拟合数据和原始数据对应点的相对误差绝对值不超过5%的点数占总点数的比例。随后,利用平均绝对百分比误差(Mean Absolute Percentage Error,简称MAPE)、合格率、相关系数(R2)、调整后R2对不同方案拟合效果进行分析,计算公式如式(21)~式(23)所示,得到表1。 表1 不同特征数量下的随机森林拟合性能Tab.1 Random forest fitting performance at different characteristics 由表1 知,对于训练集,特征数量为15 时MAPE、合格率、R2较优,而特征数量为8 的调整后R2较优;而从测试集来看,特征数量为8 的MAPE较优,而特征数量为5 的R2、调整后R2较优。综合考虑,认为特征数量为8的随机森林拟合效果相对更优,此时模型输入为装机容量、平均单机容量、职工人数、坝长、坝面积、有效库容、总库容、机组台数,计算得到各电站运营难度系数如表2所示。 由表2 可知,实例电站中运营难度系数最低的为18 号水电站,其值为32.4,表明该电站客观条件下的运营难度相对较低;运营难度系数最高的为34号水电站,其值为351.3,表明该电站客观条件下的运营难度相对较高。 表2 案例电站运营难度系数Tab.2 Typical power plant operation difficulty 为进一步了解案例电站运营难度系数分布情况,以50个运营难度系数为区间长度,对案例电站运营难度系数进行划分,绘制案例电站运营难度系数分布如图4 所示。可知,本实例中有44.8%的电站运营难度系数位于[50,100]区间内,各有11.9%的电站运营难度系数位于[100,150]和[200,250]区间内,其余电站较为平均的分散至各区间。可见,本次计算实例中的电站运营难度相对较低。 图4 案例电站运营难度系数分布Fig.4 Typical power station operation complexity coefficient distribution 4.3.1 单指标计算 分析收集资料情况,以能评价尽可能多的指标为目标,形成容纳65 个电站的实例评价数据集,评价指标按照系统性原则、代表性原则、可行性原则选取,尽量使指标能够有层次、多维度的全面反映水电站运营情况[21]。最终选取指标劳动力密度S1、每运营难度系数成本投入S2、上网电量密度S3、利用小时密度S4,计算方法分别如式(24)、式(25)、式(26)、式(27)所示。 (1)劳动力密度S1。 式中:S1为劳动力密度,其值为评价期末的每人员运营难度系数投入职工数;N为期末职工总人数;EC为人员运营难度系数。 (2)每运营难度系数投入成本S2。 式中:S2为评价周期内每运营难度系数投入成本;C为评价周期内的总投入成本;OC为运营难度系数;该指标可衡量每运营难度系数电站∕企业投入的总运营成本,以了解企业整体成本投入水平。 (3)上网电量密度S3。 式中:S3为上网电量密度,其值为电站评价周期内上网电量Em与运营难度系数OC的比值。 (4)利用小时密度S4。 式中:S4为利用小时密度,其值为电站评价周期内装机利用小时数tg与运营难度系数OC的比值。反映了排除了电站装机影响下的单位能效水平。 对指标按式(28)归一化至[0,1]区间,得到65 个电站评价指标值如表3所示。 表3 评价集电站归一化指标值Tab.3 Evaluate the normalization indicator value of the collector station 由3可知,在数据集中,每运营难度系数劳动力投入指标S1以>0.6 居多,而每运营难度系数电量产出S3以<0.2 占大多数,因此若单纯利用数值大小均分指标区间作为等级划分标准将不利于科学评价,应考虑采用其他方法。 4.3.2 等级划分 基于上述分析,采用排序法进行等级划分,将每个指标划分为差、较差、合格、较优、优5 个等级,分别以排序前20%,40%,60%,80%的指标值作为等级划分节点,得到各指标等级划分区间如表4所示。 表4 评价指标等级划分Tab.4 Evaluation indicator level division 4.3.3 综合评价 利用熵权法,将归一化指标值代入式(14)、(15)计算得到各指标在综合评价中应赋予的权重,分别为0.211、0.364、0.081、0.344。 以评价集1 号电站为例,其各指标值及其对应等级关联度如表5所示,为了避免单一评价方法的误差,将传统隶属等级和改进综合隶属等级按比重形成混合综合评分,得到各电站综合评分值并降序排列,详见图5。 图5 评价集电站归一化指标值及综合评分情况Fig.5 Evaluate the normalization indicators of the collector station and the comprehensive score situation 表5 电站1的评价指标关联度及其综合等级评分Tab.5 Evaluation index corretion of power station 1 and its comprehensive level rating 进一步分析受评电站详细情况,以劳动力密度为例,8、5、62 号水电站实际用工人数分别为148、126、119 人,若仅以用工人数为评价准则,显然其优劣排序与现有评价相反;而综合考虑电站运营的难度,8、5、62 号水电站装机分别为63、12.9、3万kW,其运营难度系数计算为8 号>5 号电站>62 号电站,与实际情况相符,故考虑运营难度系数后的指标排序更合理。 同时,对指标排序最后一位的18 号水电站进行分析,该电站装机较小属于常规分类标准的小(II)类工程规模,是本次评价集中运营难度系数最低的电站,其正常劳动力投入应属于一个较低水平;经分析,该电站投产时间早,在早期运行过程中,水电站智能化水平较低,多需要人工监测;虽然后期电站智能化水平得以提升,囿于退休职工人数随投产时间而积累,故导致单位运营难度系数用工成本较高。 同时为了验证评价结果合理性,将综合评分与当年电站考核情况进行对比,发现结果大体相似,但各水电站整项考核工作(排除资料收集工作)均开展了近半年,前前后后花费了较大人力、物力、财力,而本研究提出的方法基于已有参数资料的情况下,仅需收集与评价指标相关的实时数据,将数据输入本文构建的基于运营难度系数的对标评价模型中,即可得到科学合理的考核结果,可为水电企业摸底考核、寻优补差提供指导。 在能源结构持续转型升级的背景下,提升存量水电运行管理水平愈发重要。本文探索性地将水电站标准化运营管理与水电站综合评价有机结合,以西南区域部分水电站为研究对象,利用可控合理运营成本初步描述了水电运营难度系数基础概念,通过随机森林法构建运营难度系数模型,在此基础上输入评价集电站进行指标计算,结合信息熵赋权、改进可拓学方法得到评价结果,与企业自评估成果大致相符,显示研究提出的基于运营难度系数的标准化运营管理评价办法具备合理性。本研究在一定程度上实现了水电站横向比较,为企业寻优补差提供了方法借鉴。 由于企业目前实际运行中精细化水平不高,成本记录比较粗糙,无法提供解构后的成本分类有关记录,在未来精细化数据的支撑下,可进一步构建分项运营难度系数模型,计算设备、材料、技术、人工的分项难度系数,使评价结果更具有问题指向性,更有利于实现水电站标准化运营管理评价的目的。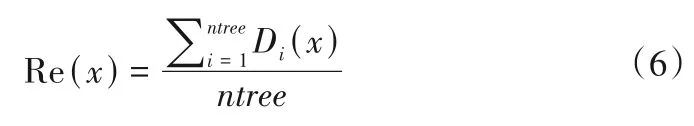
3 水电站标准化运营管理评价
3.1 基于熵权-可拓的综合评价方法


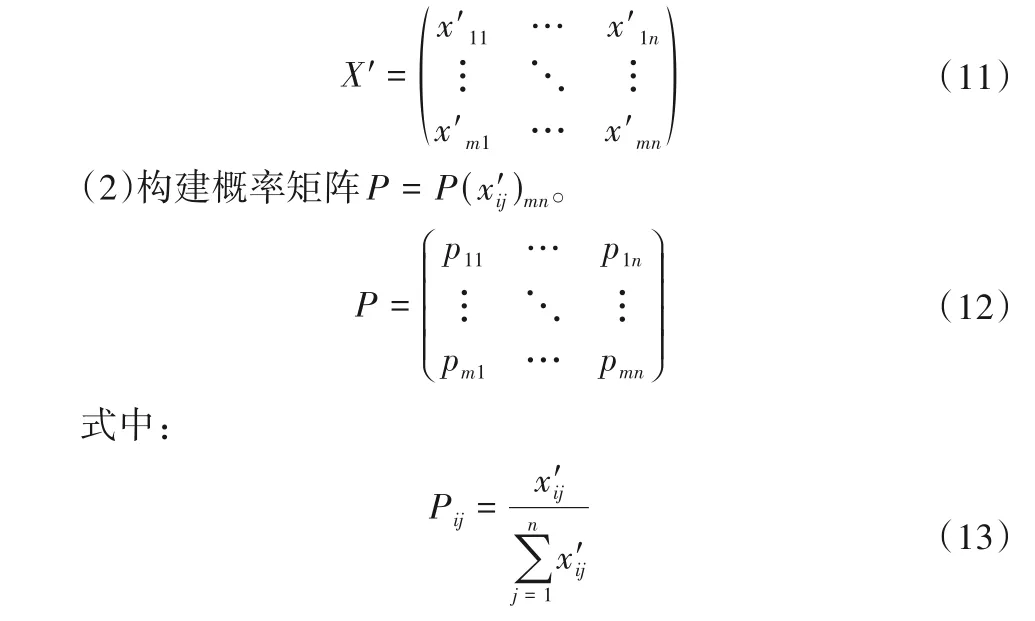
3.2 基于信息熵的赋权法
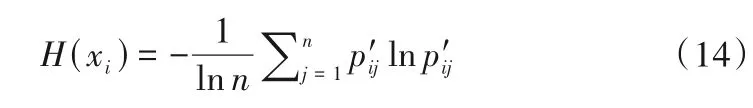
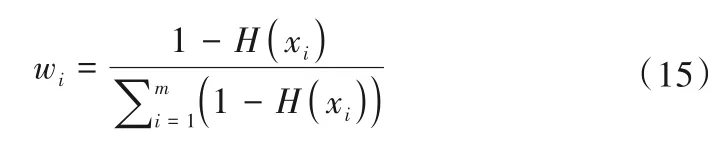
3.3 综合评分方法

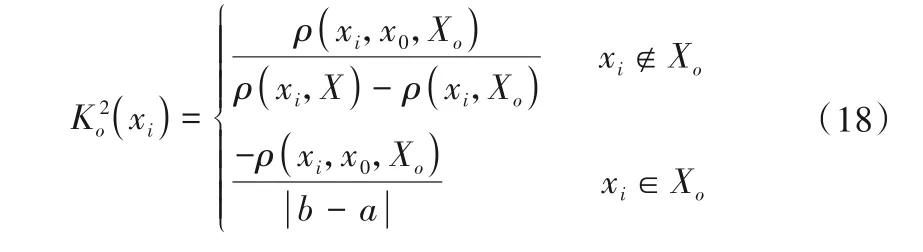
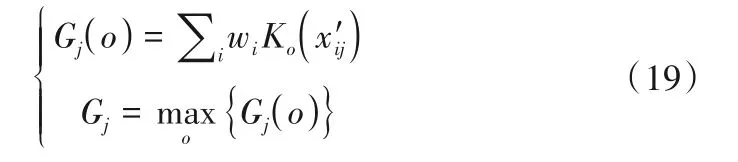
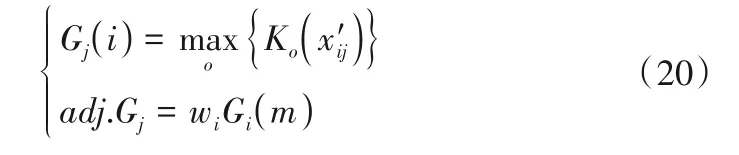
4 实例分析
4.1 参数设置
4.2 结果分析
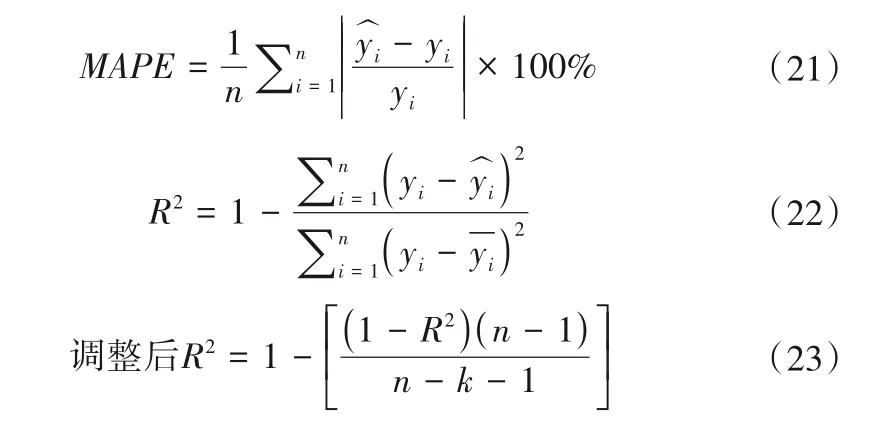
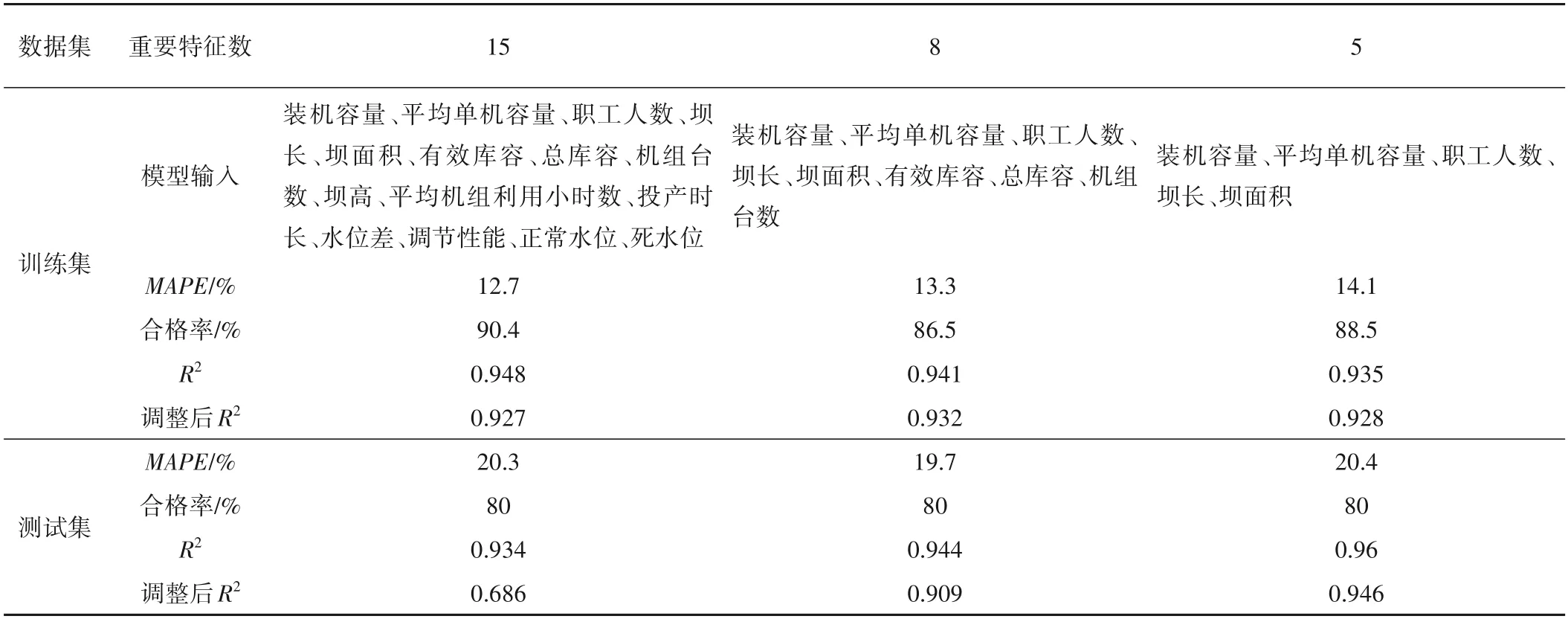
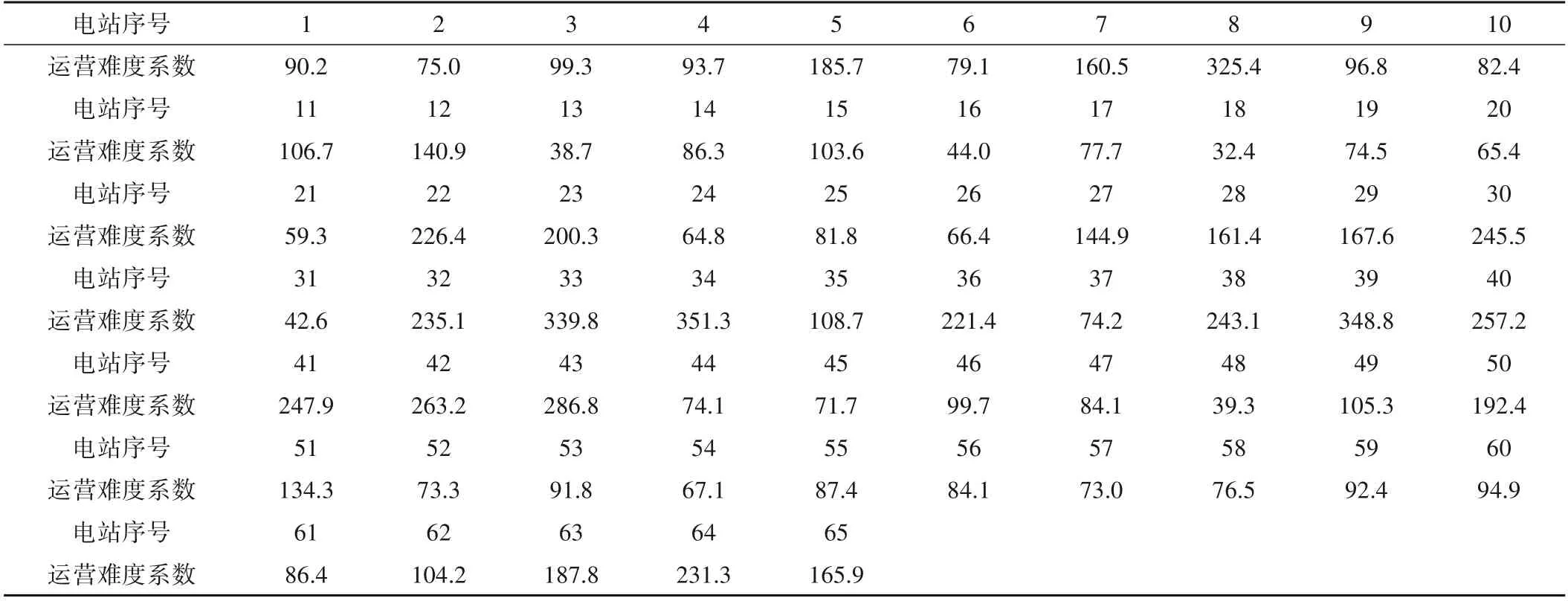
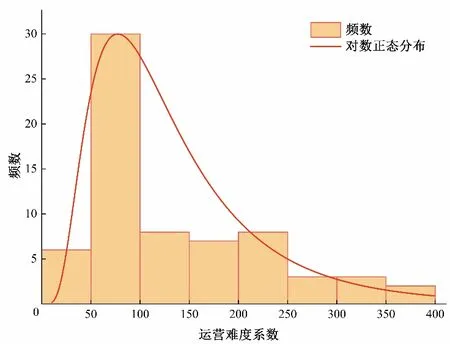
4.3 指标计算与等级划分




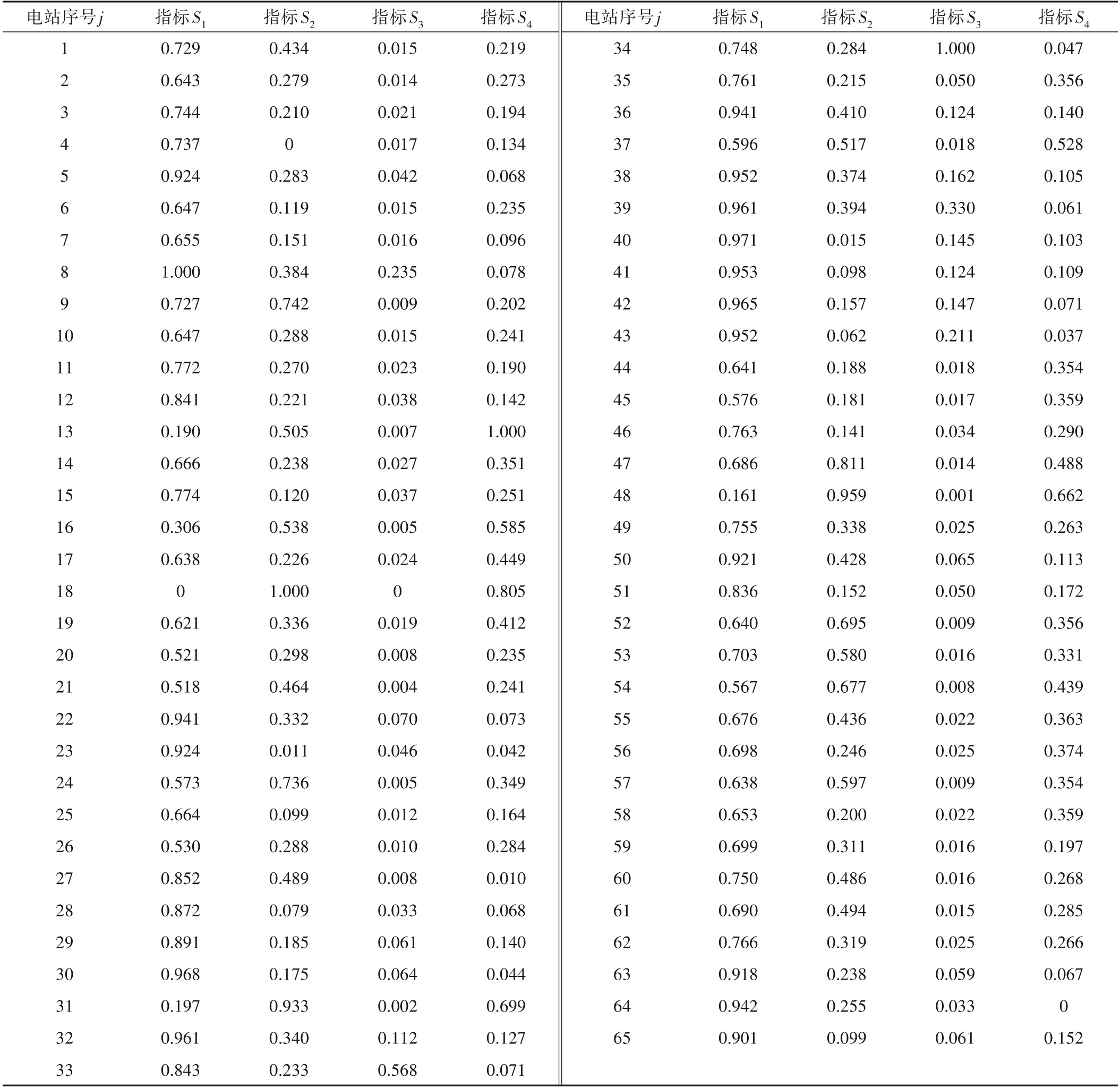
5 结语

