淹没坝田水流特性和物质交换规律研究

武梦爽，杨中华，向 珂，2，白凤朋，3，张 为

（1.武汉大学水资源与水电工程科学国家重点实验室，湖北武汉 430072；2.清华大学水沙科学与水利水电工程国家重点实验室，北京 100084；3.长江水资源保护科学研究所，湖北武汉 430051）

0 引言

丁坝广泛应用于航道整治和河道生态修复工程中，具有增加河床深度，改善航道条件和水生生境的作用。近年来，随着生态文明建设的加强，丁坝的生态效应受到广泛的关注，在大型河流整治工程中，利用淹没丁坝群来恢复河流退化的鱼类栖息地，增强河流生态系统的多样性［1］。在丁坝群中，相邻丁坝间形成坝田，坝田内流速较低，水体在坝田滞留。在坝田内，悬浮颗粒物的局部停留时间增加，加速浮游植物的生长和繁殖，为植被的生长提供条件。坝田内的水流特性是影响栖息地地貌特征、生物种群分布规律的关键因素，对适宜生境的形成有着重要作用［2-4］。国内外学者围绕坝田的水流结构和物质交换规律开展了大量的研究。许多学者通过试验和数模研究发现非淹没情况下坝田内的流动可以视为一种水平二维运动，其环流模式与坝田的体型密切相关［5-7］；并且通过对坝田和主渠之间的混合层水动力特性的研究发现，混合层内的拟序结构控制着坝田和主渠间的物质交换［8-10］。基于此，部分学者开展了对淹没坝田的研究：McCoy 等［6，11］利用大涡模拟比较了淹没和非淹没情况下单个坝田的水流特性、涡结构及物质交换，发现淹没情况下坝田及其周围区域的水流运动和涡系更加复杂，横向混合层和垂向混合层的发展及其驱动坝田和主渠进行物质交换的作用机制是相似的，但淹没状态下的交换速率更快；Yossef等［12］通过水槽试验重点关注了连续淹没坝田二维水流结构，并对坝田环流模式、混合层水动力特性和紊动特性的参数化方法进行了研究。刘易庄等［13］通过水槽实验对淹没单一坝田不同间距的水流结构进行了研究，结果表明丁坝间距对坝田内涡旋中心位置及涡量分布有着显著影响。

随着生态保护需求的提升，非淹没高丁坝在工程中的应用越来越少，工程中常采用高淹没度的低矮的潜坝［14］，在起到河势调整作用的同时避免对河流生境造成过大的扰动。已有关于淹没坝田的研究集中于低淹没状态，淹没度（水深∕丁坝高度）均在1.5 以内，并且淹没度对坝田水流特性和物质交换过程的影响机制并不明晰，因此本文通过数值模拟研究了单一坝田不同淹没度下坝田水流特性和物质交换规律，为河道生态修复工程的设计提供一定的理论参考。

1 模型建立及验证

1.1 模型建立

本文采用刘易庄等［13］的试验为算例对模型进行验证，试验水槽长16 m，宽0.4 m，高0.5 m。验证工况参数为丁坝长W=0.05 m，厚B=0.01 m，高hg=0.18 m，丁坝间距L=0.15 m，所形成的坝田宽长比为λ=W∕L=0.33，是航道整治工程中常用的布置方式［12，15］，上游丁坝设在x=0 m位置处。流量Q=57.6 m3∕h，进口流速U=0.20 m∕s，水深H=0.20 m。根据试验工况参数最终确定计算域为5 m×0.4 m×0.3 m（如图1 所示），其中水和空气的组分比为2∶1。网格布置如图2 所示，采用结构网格对计算域进行划分，并对坝田附近网格进行局部加密，所用总网格数为346 536个。

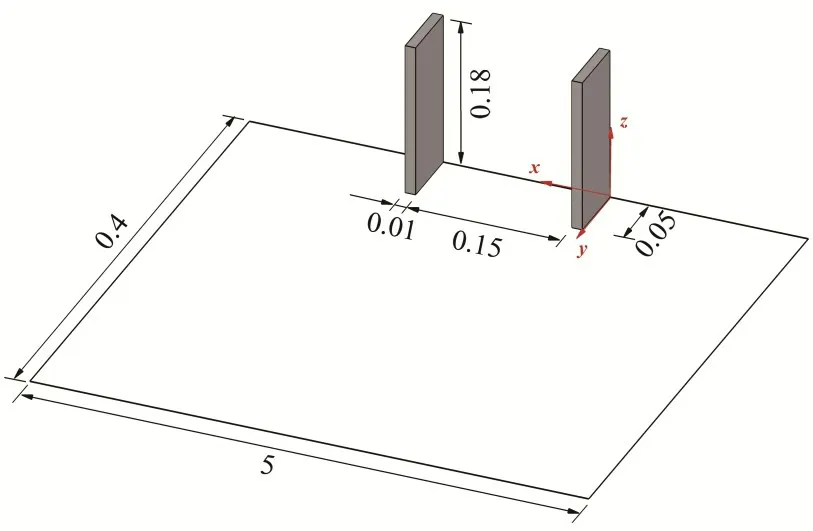
图1 数值几何模型（单位：m）Fig.1 Numerical geometric model

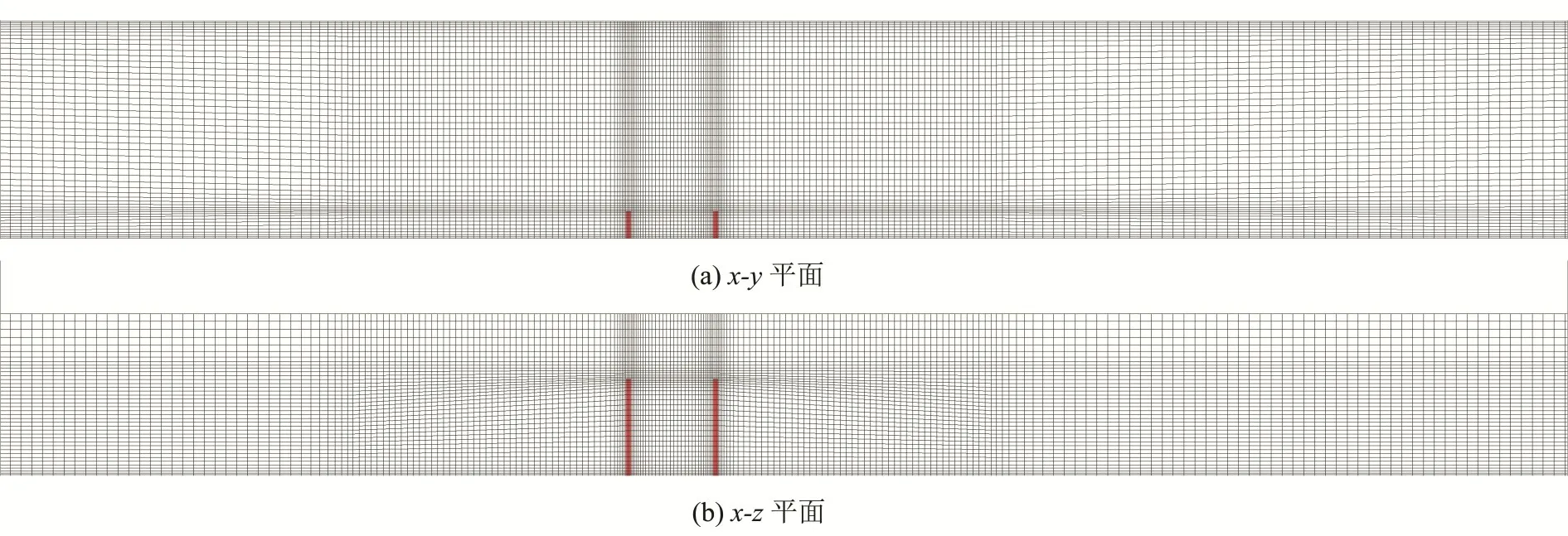
图2 计算网格布置图Fig.2 Computational mesh

1.2 边界条件及求解方法

整个计算区域设置初始水位0.2 m。边界条件为进口设空气和水流两个进口，均设置为速度进口，流速为0.2 m∕s；出口为自由出流，计算域顶部按刚盖假定的方法处理，其他设为固壁边界。

基于商业求解器Fluent（版本14.5）对单个坝田水流特性和物质交换规律进行研究。Fluent使用有限体积法对连续性方程和雷诺时均N-S 方程进行离散，并采用RNG k-ε 模型来封闭方程组。与标准k-ε 模型相比，RNG k-ε 模型能够更好地预测分离流、二次流和旋流等复杂流动，近年来，许多学者采用RNG k-ε模型研究了丁坝附近的流动［16-19］。

自由面的追踪采用隐式VOF 方案，近壁流动采用标准的壁面函数法。采用PISO算法作为压力-速度耦合算法求解离散的动量方程，压力差值的离散采用PRESTO 格式，体积分数、湍动能及耗散率的离散采用二阶迎风格式［20］，收敛标准为计算各变量残差小于0.000 1。

1.3 计算结果分析

试验采用PIV 系统测量了3 个不同相对水深平面的流场，图3 给出了数模和试验结果的流场图对比，可以看出，在z=1∕6hg平面和z=1∕2hg平面上，存在一个顺时针涡旋，随着相对水深的增大，涡旋尺度减小，在z=5∕6hg平面上，由于受到坝顶的影响，流态混乱，不易形成涡旋。数模计算的流速场与试验结果吻合较好。图4 展示了数模结果和试验数据的流速对比；在z=1∕6hg平面上沿流向在坝田内的上游、中游以及下游位置选取了对比位置（即线s1-s1、s2-s2及s3-s3），并对试验数据附上了10%的误差线。可以看出数模结果与试验数据具有一致性，但由于数值模型未考虑液体的表面张力，并且试验可能存在一定的测量误差，因此部分区域流速对比误差大于10%。结合流场和流速对比来看，数模的整体流场和流速分布均接近试验结果，说明本文所建立的数值模型可以较好地模拟淹没双丁坝附近的流场。基于此模型，进行本文工况的模拟。

图3 数模与试验的流场对比Fig.3 Velocity vector comparison between experiment and numerical model

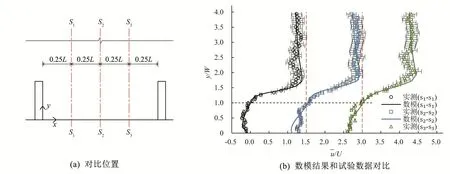
图4 数模与试验的时均流向速度对比Fig.4 Time-averaged flow velocity comparison between experiment and numerical model

2 数值模拟分析

2.1 工况设置

淹没度不同，水流运动的复杂性不同。已有研究的淹没度较小，但实际工程中的淹没丁坝常处于高淹没状态，因此本文选取了从低淹没状态到高淹没状态的四个淹没度（分别为1.11、1.6、2、2.5）进行研究。丁坝体型、布置形式及水流条件与刘易庄等［13］的试验保持一致，具体工况设置见表1。

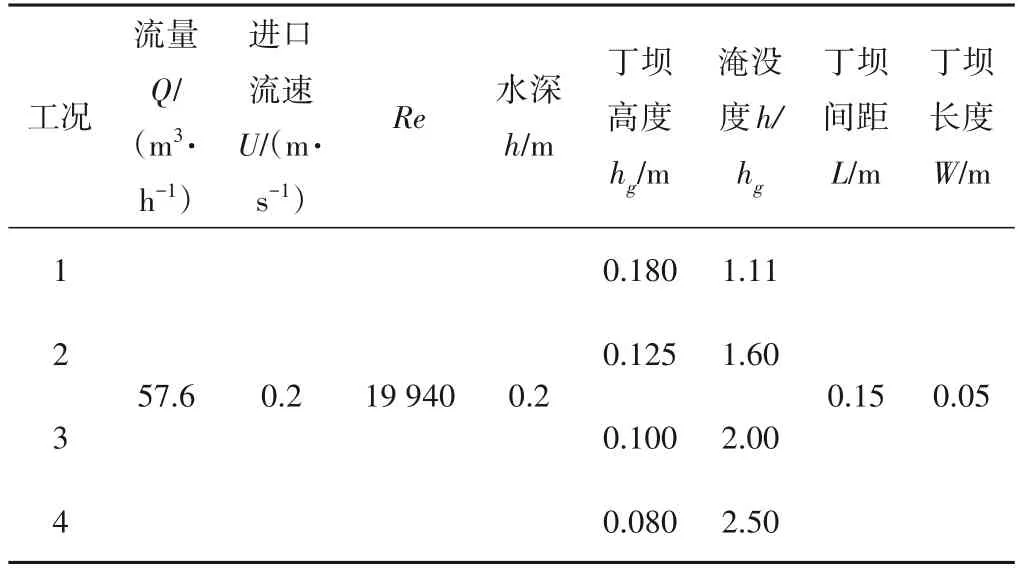
表1 工况设置Tab.1 Case setting

2.2 计算结果分析

2.2.1 环流结构

图5展示了不同高程平面（z=0.1hg；z=0.5hg；z=0.9hg）上的二维时均流线，图中，，m∕s。可以看出，淹没条件下坝田水流的三维性很强，流线特性沿水深发生变化。

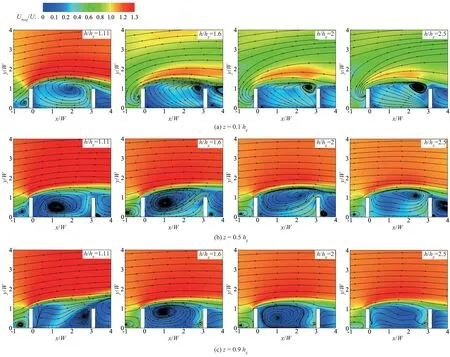
图5 x-y平面时均流线图Fig.5 Mean velocity streamlines in x-y planes

在近底面（z=0.1hg），淹没度为1.11 时，坝田内存在着明显的横向环流，旋心在坝头连接线上，并且靠近下游丁坝；当淹没度增大时，环流结构发生改变，下游丁坝坝头附近存在一个小尺度横向环流。在一半丁坝高度平面（z=0.5hg），4 种淹没度下均存在单环流结构，环流几乎占据了整个坝田，并且环流中心随着淹没度的增大向主渠方向靠近。在坝顶附近平面（z=0.9hg），淹没度为1.11时，下游丁坝和侧壁的角落存在一个横向环流；淹没度为1.6和2时，坝田内存在较为相似的环流结构，环流中心均靠近上游丁坝；淹没度为2.5 时，坝田处于高淹没状态，坝顶附近平面的流线相对平行，不存在横向环流。

图6 展示了不同纵剖面（y=0.2W；y=0.5W；y=0.8W）上的二维时均流线。对比不同工况下同一剖面上的流线可知，随着淹没度的增大，环流占据坝田的空间越大。淹没度为1.11 时，近壁面（y=0.2W）和一半丁坝长度平面（y=0.5W）上的环流结构基本一致，上游丁坝坝顶附近存在垂向环流，并且由于自由面的影响，下游丁坝后方的回流越过下游丁坝坝顶进入坝田；但在交界面附近（y=0.8W），坝田内呈现双环流结构，坝顶附近和坝田中下部均存在垂向环流，两个环流尺度相当。淹没度为1.6和2时，流线特性沿横向变化不大，坝田内存在单环流结构，环流中心靠近坝头连线和下游丁坝。淹没度为2.5 时，不同纵剖面上坝田内的二维流线几乎是一样的，垂向环流基本占据了整个坝田。

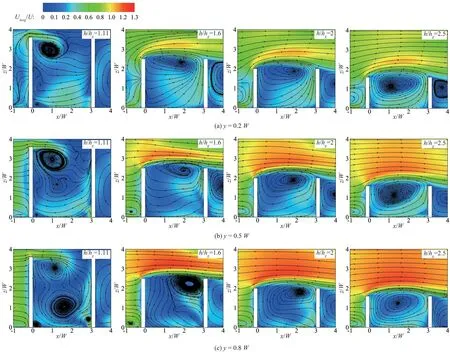
图6 x-z平面时均流线图Fig.6 Mean velocity streamlines in x-z planes

2.2.2 流速分布

为了综合反映坝田与主渠之间流速的横向和垂向分布，沿流向截取5 个截面，位置选取如图7 所示，参考Sukhodolov［5］的研究，引入整体平均的思想，对时均流速在空间上进行平均得到整体平均流速。在每个截面上对时均流向速度沿坝田高度（即丁坝高）进行平均得到整体平均流速的横向分布；沿坝田宽度（即丁坝长）进行平均得到整体平均流速的垂向分布。

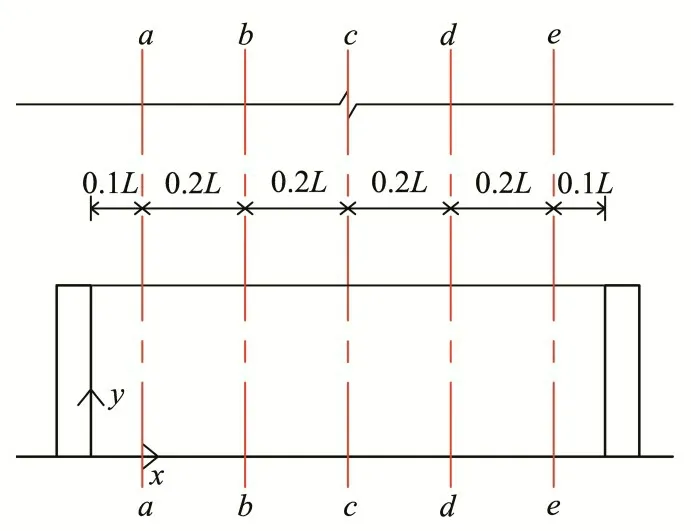
图7 截面位置示意图Fig.7 Sketch of the selected positions

图8 给出了4 种工况下不同截面上整体平均流向速度的横向分布。对比不同截面的流速分布，可知所有工况下，坝田平均流速和主渠平均流速之间的差值沿流向先增后减，在x=0.7L截面（即d-d截面）达到最大。对比不同淹没度下的流速横向分布可知，随着淹没度的升高，丁坝对水流的阻隔作用减弱，主渠平均流速减小，因此坝田内平均流速和主渠平均流速之间的差值相应地减小。总的来看，淹没度对整体平均流速的横向分布的影响主要体现在流速大小而不影响其分布形状。

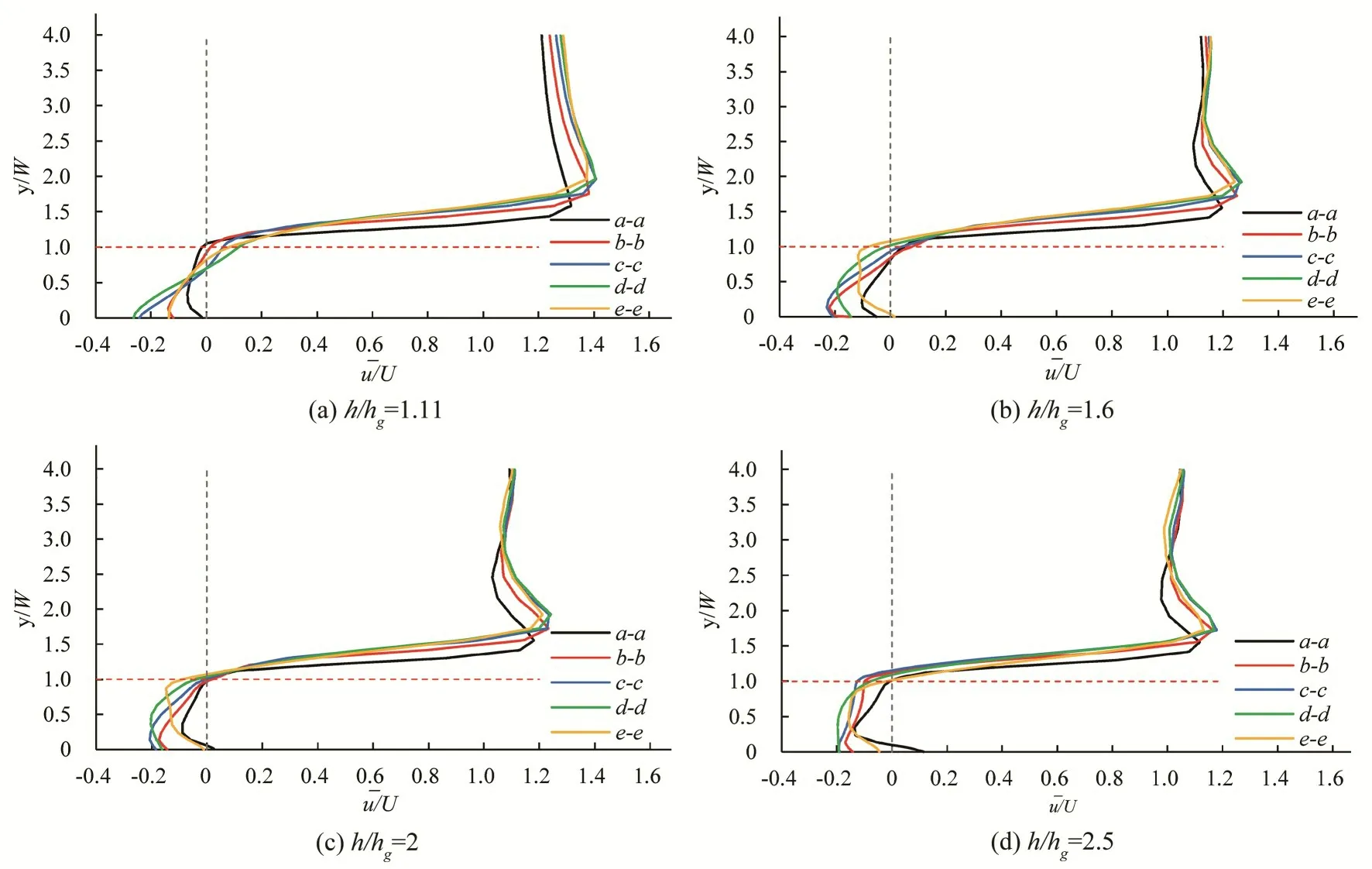
图8 整体平均流速横向分布Fig.8 Ensemble-averaged streamwise velocity along the y-direction

图9 给出了4 种工况下不同截面上整体平均流向速度的垂向分布。当淹没度h/hg=1.1 时，由于自由水面距坝顶的距离较小，受到自由水面的限制，流速的垂向分布与其他工况下的明显不同，坝田和主渠的流速差沿流向不断缩小，并且在靠近下游丁坝的截面上，坝顶以上区域时均流速为负值，这是因为下游丁坝后方的部分回流水流越过坝顶进入坝田［如图6（a）、（b）所示］，这种现象随着淹没度的升高消失。当淹没度为1.6、2 和2.5 时，坝田内的回流速度沿流向先增后减，在x=0.7L截面（即d-d截面）达到最大。随着淹没度的升高，自由水面与坝顶的距离增加，靠近自由表面的流速沿流向逐渐趋于均匀。

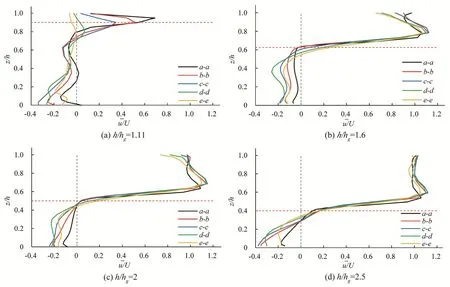
图9 整体平均流速垂向分布Fig.9 Ensemble-averaged streamwise velocity along the z-direction

2.2.3 混合层厚度

由于坝田与主渠之间存在明显的速度差异，在交界面位置会形成混合层；一般采用混合层厚度δ来描述环流与主流之间的大流速梯度范围及其对应的扩散角。横向混合层厚度δl按照以下公式定义［8］：

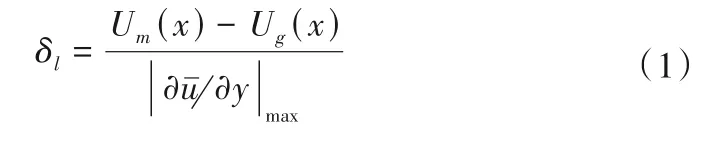
式中：Um(x)和Ug(x)分别为主渠和坝田流向坐标x处的整体平均流向速度；Um(x)和Ug(x)对应的y轴坐标是速度梯度绝对值小到可以忽略的位置，参照Mignot 等［8］的研究，本文选取0.5 s-1作为流速梯度阈值为交界面上各流向位置x所对应的最大速度横向梯度。

类比横向混合层厚度的定义式，将垂向混合层厚度δv按照以下公式定义：

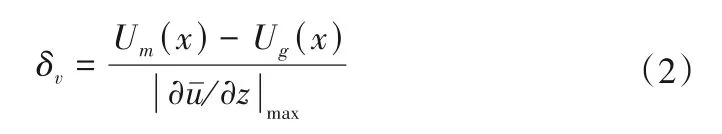
图10 展示了4 个工况下横向混合层和垂向混合层厚度沿流向发展。对于横向混合层，当x<0.5L时，混合层厚度整体上沿流向呈现线性增加的规律；当x>0.5L时，混合层厚度沿流向的增长率放缓。随着淹没度增大，坝田和主渠之间的速度差不断减小，因此混合层厚度及其增长斜率也减小。对于垂向混合层，需要说明的是，当淹没度为1.1 时，自由液面限制了垂向混合层的发展，混合层厚度远小于其他3种工况，并且受到下游丁坝后方回流的影响，在坝田下游已经不存在垂向混合层，因此图中只展示了其他3 种工况下的垂向混合层厚度沿流向的演变。3个工况下，混合层厚度沿流向不断增加；并且随着淹没度的升高，混合层厚度相应地增加。

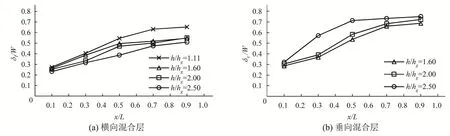
图10 不同工况下混合层厚度沿流向的演变Fig.10 Streamwise evolution of the mixing layer thicknesses for different cases

淹没度升高，混合层的水动力特性发生改变。混合层厚度越大，混合层内拟序结构典型尺寸越大，通过混合层的质量交换效率越高［21］。在本文模拟工况参数下，随着淹没度的升高，横向混合层厚度减小，垂向混合层厚度增加。低淹没状态下（h∕hg=1.11），横向混合层的厚度大于垂向混合层，因此横向混合层在物质交换过程中处于主导地位，横向混合层中的拟序结构控制主渠和坝田之间的质量和动量交换。随着淹没度的升高，垂向混合层发展，在高淹没状态下（h∕hg=2.5），垂向混合层厚度大于横向混合层，此时垂向混合层在物质交换过程中处于主导地位。

2.2.4 交换系数

经典的坝田物质交换理论认为，坝田与主渠之间的质量交换效率与两区域之间的物质浓度差异成正比［7］，即：

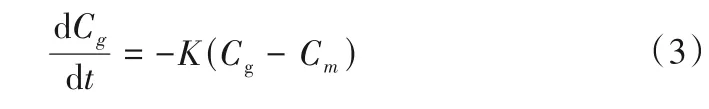
式中：Cg为坝田内的浓度；t为时间；Cm为主渠的浓度；K为质量交换系数，s-1，是定量描述坝田与主渠之间混合过程的常用指标。

对于有初始浓度的坝田，主槽水流的卷吸作用会将物质带出坝田，坝田浓度下降梯度与剩余浓度成正比，比例系数即为交换系数。因此在初始时刻在坝田引入浓度为C0的物质，并假设主渠浓度为0，对式（3）进行求解，可以得到：

式（4）说明了交换系数K代表着坝田和主渠之间的交换速率。

基于已建立的水动力模型，在水流充分发展后，利用Flunet中的UDS 功能在坝田内瞬时均匀地引入标量物质，此时设定为初始时刻，坝田内无量纲标量初始物质浓度为1，主渠浓度设定为0，监测坝田内空间平均浓度随时间变化过程直至99%的物质离开坝田，绘制坝田浓度（体积平均浓度）随时间变化曲线（对数坐标），曲线的斜率即为质量交换系数K［6，9］。

图11 给出了坝田平均浓度随时间变化曲线。由图11 可知，坝田内的浓度以指数型下降，坝田和主渠之间的交换存在两个阶段。当坝田内的浓度降至50%～40%，交换系数发生改变。这一现象与McCoy 等［11］的研究具有一致性。第一个阶段物质浓度快速下降，交换系数大，这由通过混合层的直接交换控制的；第二个阶段浓度下降速率放缓，交换系数减小，这是由于物质位于环流中心，此时混合层内的大尺度结构无法渗透到环流中心。

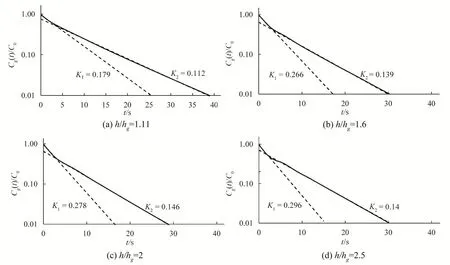
图11 坝田平均浓度随时间变化过程Fig.11 Variation process of volume average concentration in groyne field with time

对比4 个工况下的交换系数，可以发现第一个阶段的交换系数K1随着淹没度的升高而增大。当淹没度为2.5 时，混合层整体厚度达到最大，混合层内的涡体侵占了坝田内更多的水体，因此淹没度为2.5 时交换效率最高。第二个阶段的交换系数K2随着淹没度的升高先增后减，在淹没度为2时达到最大。

3 结论

通过数值模拟对不同淹没度下坝田的环流结构、流速分布、混合层厚度和交换系数进行了研究，得到了淹没度对坝田水流特性和物质交换的影响。

（1）淹没条件下坝田内存在横向环流和垂向环流；淹没度对流速的横向分布的影响主要体现在流速数值大小而不影响其分布形状。

（2）横向混合层的厚度随着淹没度的升高而减小，而垂向混合层的厚度随着淹没度的升高而增大。低淹没状态下，坝田主要通过横向混合层与主渠进行交换，高淹没状态下，坝田主要通过垂向混合层与主渠进行交换。

（3）不同淹没度下，坝田和主渠之间的交换均存在两个阶段，第一个阶段交换速率大，交换系数随着淹没度升高而降低，第二个阶段交换速率放缓，交换系数随着淹没度升高先增后减。