基于GRU-BP 组合模型的湖泊水位预测方法探索

刘惟飞，陈 兵，余 周

（1.华南理工大学环境与能源学院，广东广州 510006；2.广东省环境风险防控与应急处置工程技术研究中心，广东广州 510006）

0 引言

随着气候变化和城市化进程加速，城市内涝灾害越来越严重。精确的水位预测对于城市内涝预警至关重要，是解决城市内涝问题的关键技术［1］。目前常用的水位预测方法是以数据驱动的预测模型。近年来，机器学习方法中循环神经网络（Recur‐rent Neural Network，RNN）被广泛应用于时间序列预测的研究［2，3］。但是传统RNN 并不能很好地处理长时依赖问题，在训练过程容易出现梯度消失［4］。梯度消失即距离当前时间步越长，信息反馈的梯度信号越不显著。信息随时间步数增加在网络中记忆值变小的情况，这意味着RNN长时学习能力失效。而深度学习算法中的长短时记忆网络（LSTM）可以有效的改善传统RNN模型的缺陷，在近几年成为了水文时序预测的主流方法之一［5，6］。但是LSTM 存在训练时间长、参数较多、内部计算复杂的缺点［7］。因此，Cho等人于提出了LSTM 简化变体——门控循环单元（GRU）［8］。此外，组合模型理论上能够克服单一模型的局限［9］。因此部分学者利用GRU 模型和组合模型理论对传统的基于LSTM 的水位预测方法进行了优化。如：2020 年，Pan M 等［10］将卷积神经网络（Convolutional Neural Networks，CNN）和GRU 网络结构结合应用于预测长江水位变化，发现CNN-GRU预测性能优于LSTM；Miau S等［11］利用CNN-GRU 模型对台湾某河流的洪水水位进行预测，结果表明CNN-GRU 模型预测精度较LSTM、CNN分别提高了35.8%和32.3%。

为探索GRU组合模型应用于水文时序预测的有效性，本文提出了一种基于GRU 和BP 神经网络的水位预测模型。与CNN-GRU 及单一模型对比，该组合预测方法具有更好的拟合精度及稳定性，为湖泊预测水位提供了一种新的方法。

1 研究区域概况与数据来源

1.1 研究区域概况

研究区域为猎德涌的源头西湖区域，猎德涌位置重要，是广州市仅有的一条流经天河区珠江新城中央商务区的河涌，猎德涌下游沿线水位过高是造成猎德涌流域低洼处水浸严重主要成因之一［12］。猎德涌的源头西湖位于天河区华南理工五山校区内，最大水深8.9 m，集水面积0.031 km2，通过双向阀门往猎德涌排水。西湖水源主要依靠降雨或“三涌补水工程”补充［13］。日常补水流量为1.2～2 m3∕s，时间为6∶00-18∶00。西湖与猎德涌水位存在显著的相关性，源头水位变化对于研究猎德涌流域内涝具有重要的意义。猎德涌流域概况及西湖监测点位置见1（a），西湖区域见图1（b），猎德涌流域位置见图1（c）。

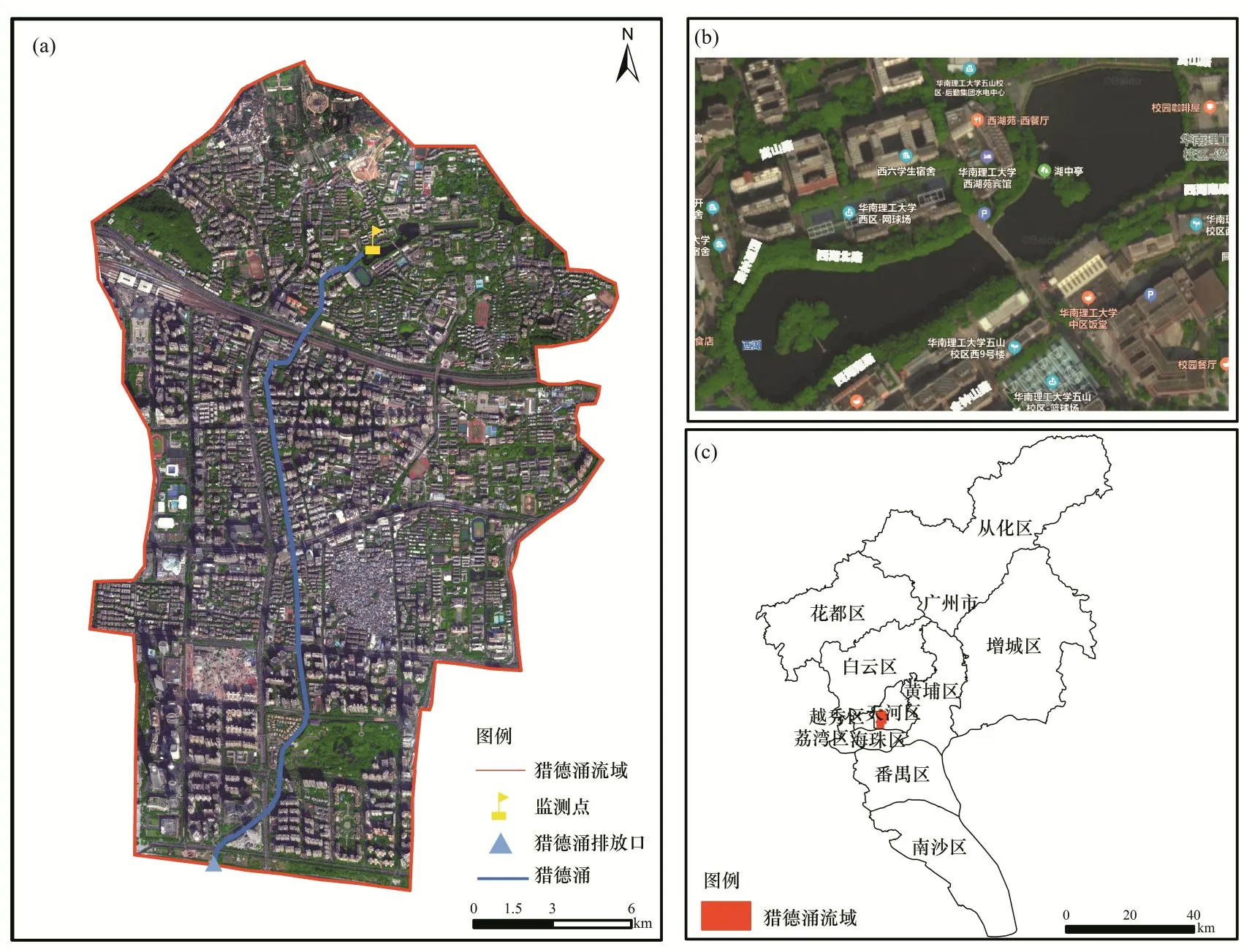
图1 研究区域概况图Fig.1 Generalized diagram of the study area

1.2 数据来源

利用课题组自主研发设计的智慧排水内涝云服务系统［14］采集的2021 年3 月11 日至8 月31 日的西湖每十分钟间隔时刻的水位值和雨量数据建立湖泊水位预测模型。包括25 056（24 h×6×174 d）组水位数据和降雨数据，其中降雨量数据允许存在零值，数据包含雨前晴天数、降雨历时等隐藏特征信息。雨量及水位数据见图2。

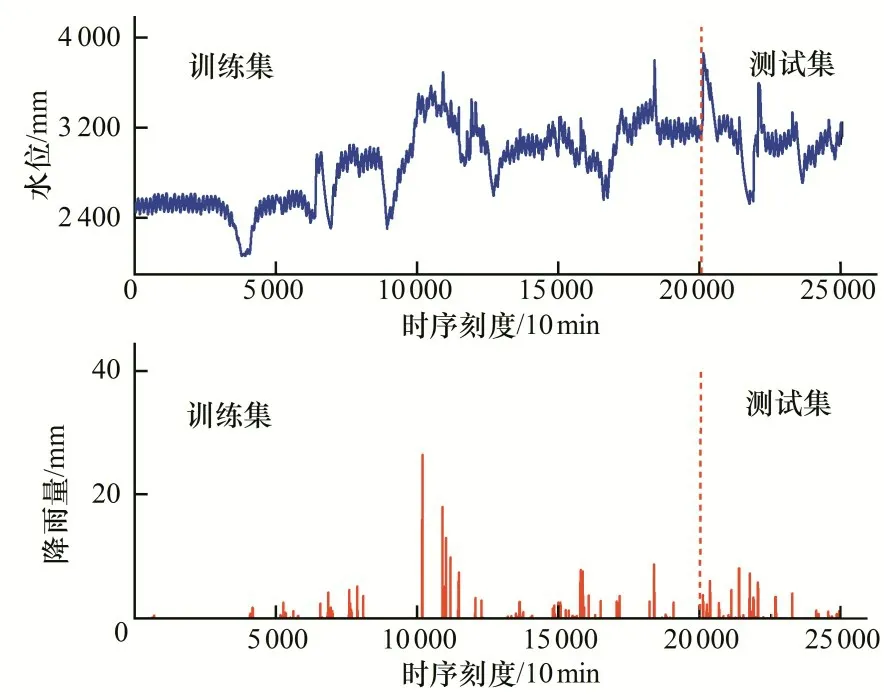
图2 监测点降雨量及水位变化Fig.2 Rainfall and water level data from monitoring stations

2 研究方法

2.1 实验环境

深度学习的水位预测模型编程语言采用python3.8实现，深度学习框架采用谷歌开发的TensorFlowCPU2.0版本。

2.2 基于GRU-BP组合模型预测步骤

组合模型的本质思想是通过多个方面和多角度的集成学习方式修正模型误差，因此能弥补单一模型的缺陷。BP神经网络已广泛用于水文时间序列预测领域，具备较强的非线性映射能力，但缺乏时序概念，而GRU 神经网络可以比较好地解决上述问题。故本文选用GRU 与BP 组合预测，组合模型技术路线见图3。

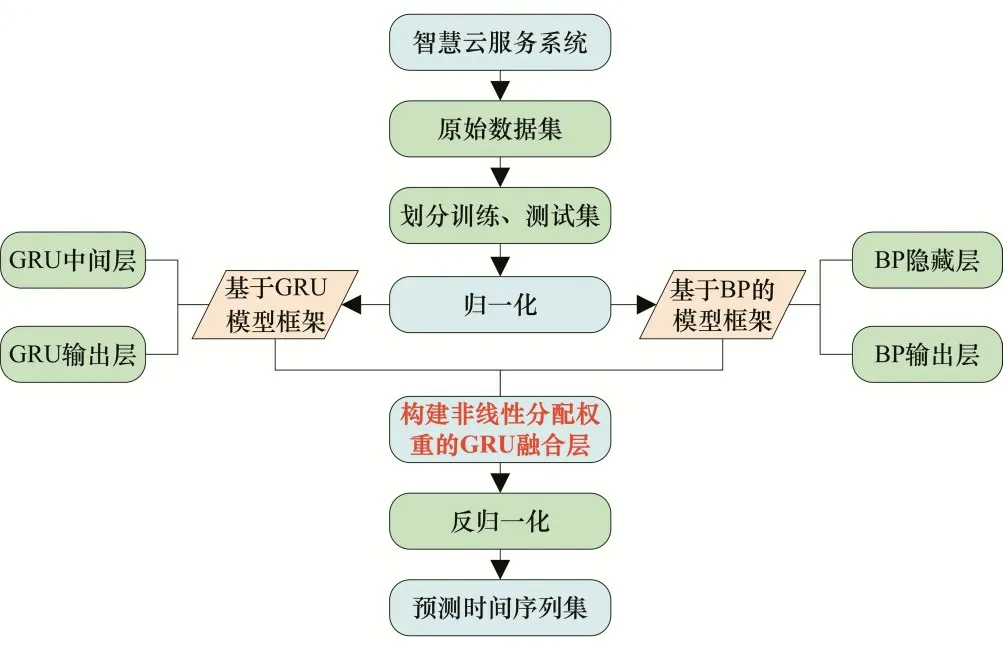
图3 GRU-BP技术路线图Fig.3 GRU-BP technology route

样本共25056 组数据，前20016 组数据（3 月11 日-7 月27日）用于训练，5 040 组数据（7 月28 日-8 月31 日）用于测试，时间间隔为10 min。为了消除雨量与水位数据间量纲影响，将训练集S及测试集T归一化。组合模型有两个输入层和一个融合输出层，采用直接预测方式，预测步长为6，即预测时长为1 h。

训练过程中，组合模型的训练集为：S==GRU-BP组合模型的测试集为：T=X为样本中的自变量，R为雨量值，Y为水位值，为因变量。

3 模型构建

3.1 模型评价指标

为了准确评估模型的精度，采用均方根误差（Root Mean Square Error，RMSE）、均方误差（Mean Square Error，MSE）和平均绝对误差（Mean Absolute Error，MAE）及平均绝对百分误差（Mean Absolute Percentage Error，MAPE）作为误差分析指标，对模型误差进行量化评价。

3.2 实验参数设置

通过控制变量法［15］依次选取模型关键参数，其中GRU融合层数始终设为1，优化方法使用均方差传播（Root Mean Square prop，RMSprop）算法。根据经验调试模型初始化参数之后，保持模型其他参数不变，每次只更改某一变量比较进行贪心式寻优，最终确定模型参数组合，见表1。

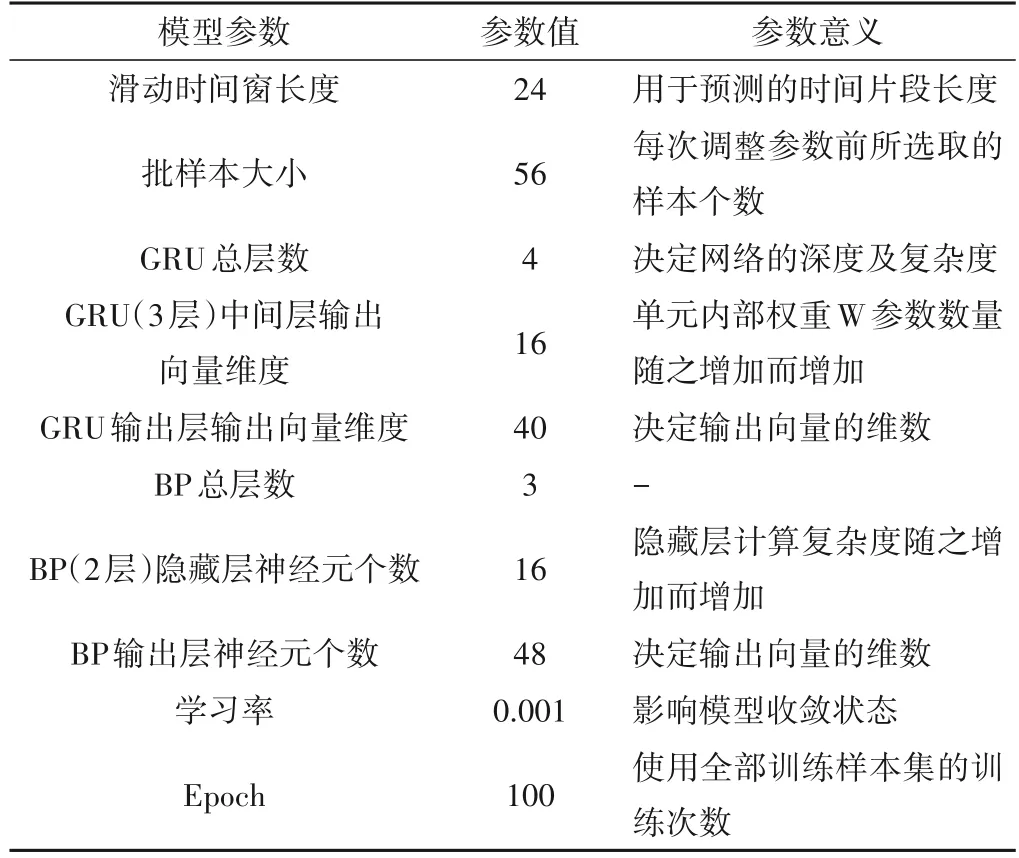
表1 模型参数设置Tab.1 Model parameter Setting

4 仿真结果分析

4.1 模型预测结果

以1 h 预测时长为例，为了验证GRU-BP 模型预测湖泊水位的优点，使用了3层中间层的LSTM、GRU模型与BP神经网络（隐藏层层数为2）以及CNN-GRU（卷积层为1 层，卷积核个数为1，卷积核尺寸为9）模型对西湖水位进行预测，并作对比分析。对比模型的超参数与GRU-BP 模型设定一致。模型预测结果见图4，误差见表2。

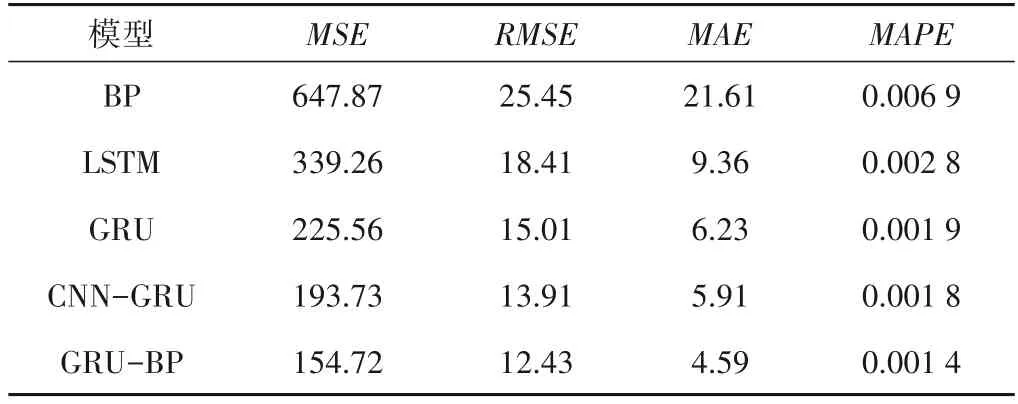
表2 不同模型预测误差指标Tab.2 Prediction error index of different models

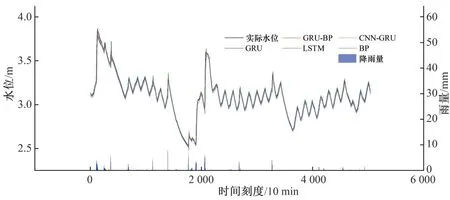
图4 不同模型预测结果Fig.4 The results predicted by different models

4.2 测试集分类分析

由图5 和表2 可知，对于测试集的整体区间水位预测，模型的预测精度从高至低依次为GRU-BP、CNN-GRU、GRU、LSTM、BP。整体的测试集可划分为降雨期和未降雨期，降雨期又分为暴雨期、大雨期、中雨期、小雨期。对比各模型在不同时期下的预测性能，评估模型在不同情况下的多因素特征学习能力。统计的降雨期数据为降雨起始时至降雨结束后一个小时之间的数据。

（1）降雨期预测。测试集包含两场暴雨、六场大雨、四场中雨、四场小雨。不同模型的预测结果分别见图5～8。

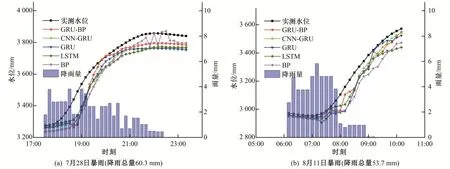
图5 暴雨时期预测结果Fig.5 Forecast result of rainstorm period

由图5～8 可知，西湖水位与补水量、排水量、降雨量相关。随着降雨总量变小，雨量与水位间的相关性减弱，水位随降雨总量减少逐渐呈现线性上升或下降趋势。

GRU-BP 的预测误差较小，在暴雨期、大雨期、中雨期及小雨期与实际水位的最大偏差分别为20、14、8、5 cm。CNN-GRU曲线拟合度优于GRU 与LSTM，GRU 与LSTM 拟合曲线在某些时期十分接近。BP模型的拟合曲线则随降雨量变化波动较大。

大雨及暴雨期间，各模型对雨强峰值段期间的水位预测精度要明显低于雨量小且均匀分布的降雨时段。当峰值雨量大于6 mm∕（10 min）时，模型在雨峰出现后1 h 时段内的预测误差显著增大；这也表明在历时短、雨强大的时段区间，模型不易挖掘多特征因素对水位增量影响。

各模型的预测精度会随着变量因素增加而减少。相似降雨总量下，由于白天时刻增加补水变量因素，模型在夜间的预测精度会优于白天。

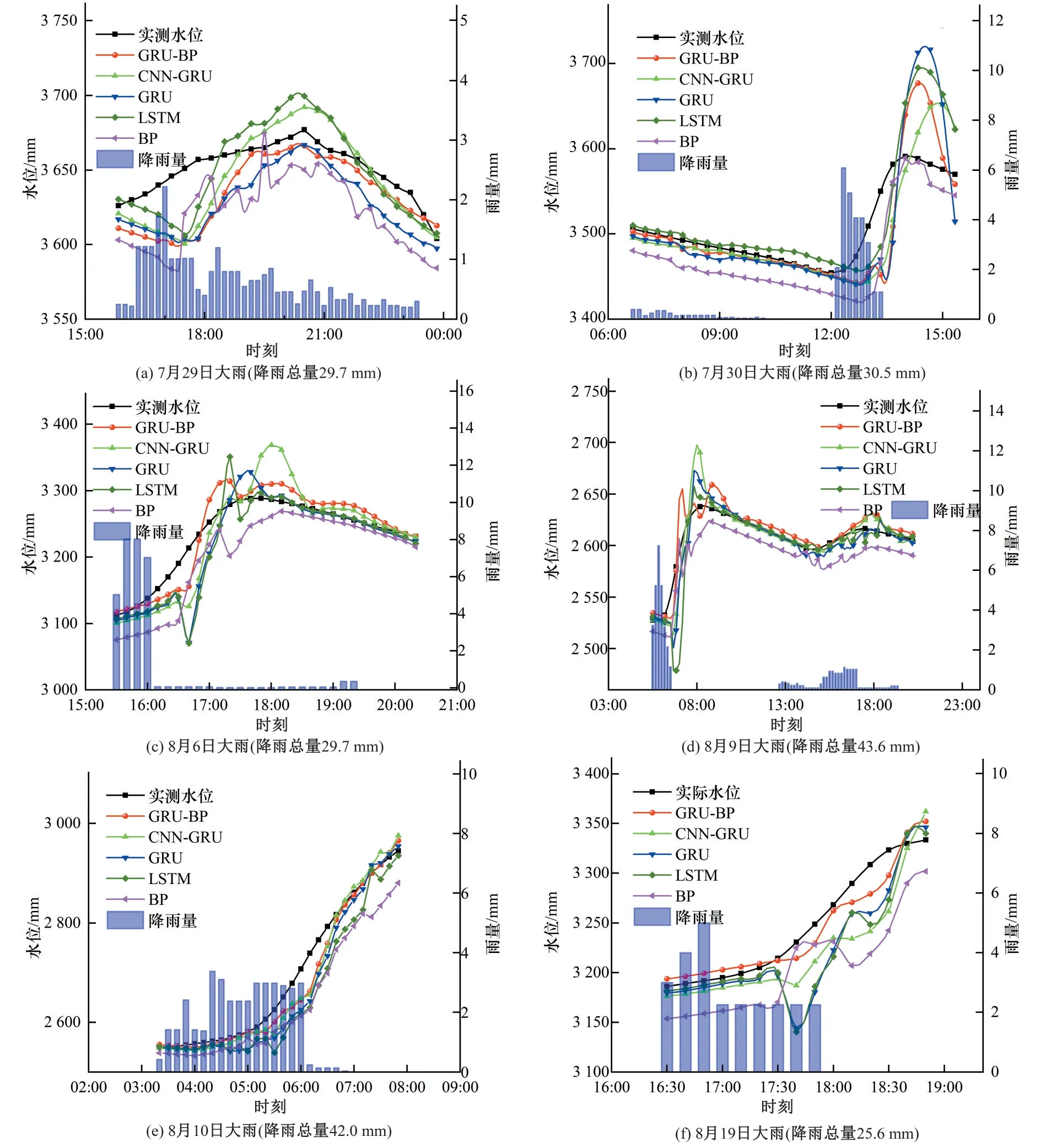
图6 大雨时期预测结果Fig.6 Forecast results of heavy rain period

（2）未降雨期预测。未降雨期，水位没有雨量因素干扰，雨量输入为零值。西湖白天的水位主要由补水量和排水量决定；傍晚至夜间的水位主要由排水量决定。未降雨期的排水量和补水量对水位的增量值为ΔY，在一段时间内基本保持恒定。此时水位波动较小，理论上可视为线性变化。将测试集中降雨时期数据剔除，计算未降雨期的预测误差。

（3）模型预测效果对比。为了方便比较模型在不同时期的预测精度，总结各模型在不同时期的RMSE值并以直方图的形式显示，见图9。

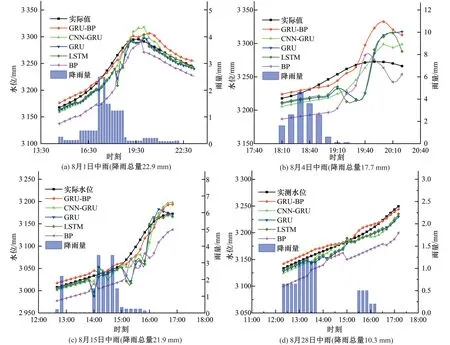
图7 中雨时期预测结果Fig.7 Forecast result of moderate rain period

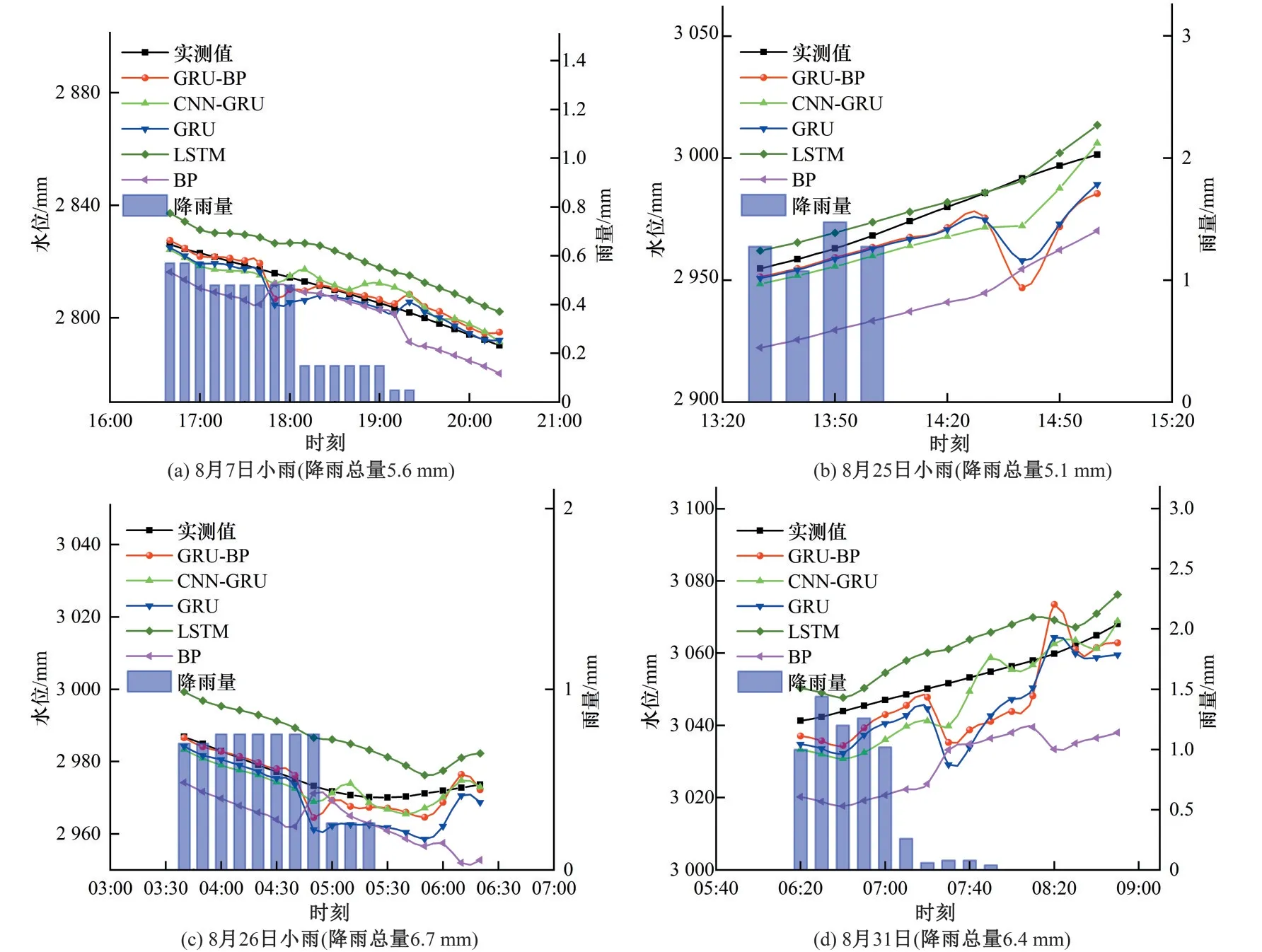
图8 小雨时期预测结果Fig.8 Forecast result of light rain period

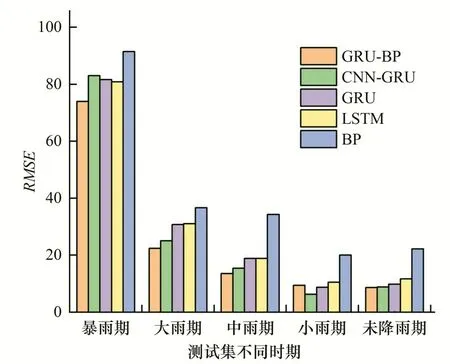
图9 模型均方根误差指标直方图Fig.9 Model root mean square error index histogram

由图9 可知，大多时期，基于GRU 和LSTM 模型的RMSE都优于BP 模型。这反映了RNN 在水文时序领域预测的优势；GRU-BP 及CNN-GRU 组合模型的预测精度都高于单一模型，且在大雨时段预测具有明显的优势。一方面原因在于，与暴雨期相比，大雨期雨量对水位增量更小，误差也更小；另一方面原因是大雨期的训练数据更多。这表明了合适的组合模型能有效集合单一模型优点并克服其局限性。

卷积神经网络能有效提取多变量特征，因而CNN-GRU 应用于多变量下的水位预测具备明显的优势［10，11］。但GRU 组件自带的特征提取能力就足以应对特征变量较少的情况，卷积组件对模型整体的预测精度提升有限。除了小雨期精度高于GRU-BP模型，整体预测精度低于GRU-BP。

大多情况下，GRU-BP模型的评价指标都优于其他的模型，具有最高的精度，特别在暴雨及大雨期预测具有显著优势。GRU-BP 水位预测模型的优势在于：在未降雨期，GRU 模型框架利用独特门控机制通过历史水位的时序变化规律学习短期内补水量、排水量对水位增量值ΔY。独特的门控机制既注重短时序列联系又可以捕捉长时序列的影响，抑制梯度消失。在降雨期，增加雨量向量值输入，GRU 以ΔY为依据进一步挖掘出三者影响因素（补水量、排水量、雨量）对水位增量值ΔY′。BP 模型框架对降雨期的雨量输入比较敏感，预测结果上有明显的峰值与低值，雨量对于水位增量影响较大，可以弥补GRU 模型某些时刻增量值ΔY学习过大的问题，增强模型降雨短时预测能力。GRU 融合层根据预测方差非线性调整GRU、BP 模型框架输出向量信息反馈的权重。该集成方式实质上能更精确考虑补水、排水时序变化及雨量等信息对水位增量影响权重，可以平衡模型的线性与非线性预测能力，并削弱某些时刻异常输出向量的干扰，提高了预测精度。

4.3 不同训练集对模型精度影响

为评价增加训练数据后各模型的水位预测性能是否有所改善，测试数据集划分与上述保持一致。基于水文时间序列数据自身的特点，利用了参数优化好的各模型，设计了3种不同的训练方案对水位进行预测，见图10（a）。模型参数保持不变，以1 h 预测时长为例，比较了3 种不同训练集数据下的拟合效果，均方根误差见图10（b）。

由图10（b）可知，对比3 种情形下各模型预测性能，GRUBP预测精度最高，特别在样本量小的时候也表现出不错的泛化能力。在训练过程中，各学习模型在增加训练数据后都表现出更好的预测性能。与用35%训练数据训练模型相比，输入65%的典型雨季期数据训练的模型预测性能提升程度最大。但在进一步将训练数据从65%提高到100%时，预测性能提升非常有限。

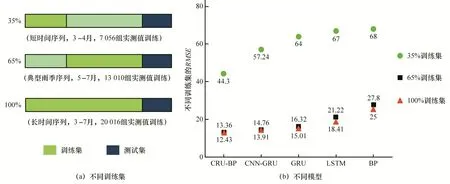
图10 不同训练集下的模型预测性能Fig.10 Model prediction performance under different training sets

4.4 不同预测时长对模型精度影响

在实际应用中，暴雨及大雨的水位预报提前期越早，防洪方法就越有效。因此本文探索了该测试集下暴雨及大雨期下最佳适应预测步长。模型参数保持不变，对比各模型在不同预测步长下的均方根误差，见图11。

由图11（a）可知，随着预测长度的增加，各模型在暴雨期的模拟误差越来越大。大多情况下，GRU-BP 的预测精度都要高于其他模型；LSTM 在部分情形下（暴雨时）的预测结果要优于GRU。与从10 min 增加到30 min 相比，预测时长从30 min 增加到1 h时，各模型的预测误差提升较大。

由图11（b）可知，组合模型的结构优势更易从大雨时期数据中挖掘与水位相对应的特征关系。当预测时长大于30 min时，可以看出单一模型（GRU、LSTM、BP）的预测误差明显增大。综合分析，各模型参数保持不变的情况下，组合模型稳定性好，模型的适用性强，不同预测步长都能达到相对稳定的预测效果。

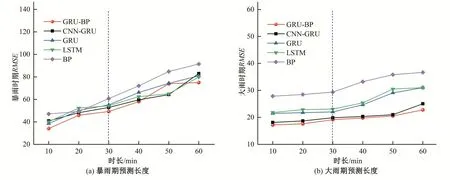
图11 预测时长对模型预测精度影响Fig.11 The influence of prediction time on model prediction accuracy

5 结论

首次尝试将GRU-BP 组合模型应用于湖泊水位预测方面并探讨其适用性。结果表明：

（1）GRU-BP 模型可以作为水位预测的简单有效工具，与CNN-GRU 相比，在暴雨期具有明显的优势。大多情况下，与GRU、LSTM 和BP模型相比，GRU-BP集成学习的组合方式拥有更高的预测精度，且分布式并联结构使得模型的适用性强及稳定性高。

（2）在缺乏足够多的样本数据支撑时，选取典型及代表性的水文数据，也可以达到较好的模型预测效果。且模型预测湖泊的暴雨和大雨期水位时，预测步长设置为30 min 最佳。在该预测步长下即可以保证有一定提前期的时间，也能获得不错的模型预测效果。