矿用电动铰接车辆驱动力分配研究
郝志军,张 凡
1山西天地煤机装备有限公司 山西太原 030006
2中国煤炭科工集团太原研究院有限公司 山西太原 030006
3煤矿采掘机械装备国家工程实验室 山西太原 030006
电 动支架搬运车作为煤矿辅助运输领域的重要搬家倒面设备,由于其绿色无污染的优点,逐渐被我国大型煤矿企业及搬家公司业主青睐。电动支架搬运车在使用中经常出现满载爬坡时轮胎打滑、牵引力不足的状况,已经成为急需解决的重要问题。电动支架搬运车采用分布式四轮轮边驱动,有效缩短了传动链,提高了传动效率,但如何合理控制和分配 4个驱动电动机的转矩,是一直以来该类车辆需要解决的难题。
目前,公路路面行驶的四轮电动汽车的驱动控制研究成果比较多且成熟,上海交通大学的郑水波等人设计了基于滑模控制理论的驱动防滑控制器,并进行了极限工况下和不同道路条件下的仿真分析;吉林大学的李洋等人[1]、清华大学的邹广才等人基于四轮独立驱动的特点建立了侧重提高车辆稳定性和机动性的新的纵向力分配方法[2];重庆理工大学的张博涵等人设计了一种自适应驱动防滑控制模糊算法,可以实现整车对路面信息的采集,并实现驱动力自适应分配[3];燕山大学的刘晶采用驱动防滑力矩分配控制策略来控制驱动力的分配[4]。这些理论和算法均是对承载质量不会导致车辆质心发生重大变化的小型整体式车辆而言,而对于煤矿井下非公路路面使用的大型铰接作业车辆,上述理论和算法不能完全适用。在非公路铰接车辆四轮驱动控制方面,北京科技大学的孙会来等人针对矿用 35 t 铰接自卸车做过相关研究,提出一种以滑移率一致为控制目标的差速控制策略,减少了轮边电驱动铰接式车辆轮胎的磨损,提高了驱动功率利用率[5]。为此,结合矿用支架搬运车质量大、载荷大、速度低等特点,研究支架搬运车在行驶过程中车轮载荷的变化以及驱动电动机输出转矩的限制,有效利用地面附着力,防止车轮滑转,提高整车的驱动性能,就显得尤为必要。
1 驱动力分配控制
分布式四轮驱动电动支架搬运车的各车轮的驱动力独立可控,车辆在不同行驶工况下对性能要求有所不同[6],因此应根据不同行驶工况制定相应的驱动力分配控制方法。
1.1 直线行驶驱动力分配
研究直线行驶时前、后轴驱动力的分配,将整车模型简化为二轮模型,仅考虑车辆沿x轴的纵向运动和沿y轴的侧向运动,如图 1 所示。图 1 中ax、ay分别为车辆的纵向和侧向加速度;Fx1、Fx2分别为前、后车轴的纵向力 (即驱动力);Fy1、Fy2分别为前、后车轴的侧向力;a、b分别为整车重心G到前、后车轴的距离;L为前轴和后轴的距离。

图1 直线行驶状态下车辆模型Fig.1 Vehicle model in linear operating mode
假设在车辆直线行驶状态下整车重心位置不变,纵向加速度由前后四轮处产生的驱动力之和来决定,并且轮胎相对于地面为直立状态,轮胎的摩擦圆半径与载荷和路面摩擦因数的积成正比。
车辆纵向和侧向的动力学方程为:

式中:m为整车质量。
利用轮胎力的摩擦圆原理,车辆前、后车轮达到附着极限的条件分别为:

式中:φ为路面附着系数;Fz10、Fz20分别为前、后轴的静态载荷。
前、后轮侧向力分别为

前、后轴的载荷转移量

式中:hg为车辆的质心高度。
由以上公式可得到前、后轴同时达到附着极限的条件为:
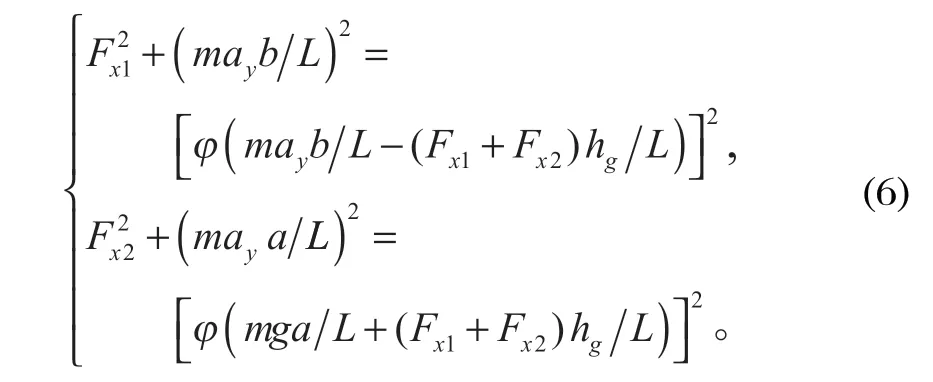
为了求出前、后轴驱动力的直接分配关系,定义后轴驱动力分配比

方程组 (6) 可以表示为

式中m、a、b、L、hg都是车辆的参数,需要确定的车辆状态参数有µ、ax、ay,要求解的是后轴驱动力分配比λ。在给定路面附着系数φ的条件下,无论直线行驶还是弯道行驶,车辆的侧向稳定性都比纵向稳定性重要,应该优先保证。根据纵向加速度ax和路面附着系数φ,求出后轴驱动力分配比λ。纵向加速度ax可以通过电动机编码器上的速度传感器得到,假设路面附着系数φ为已知条件,可以得到在不同路面附着条件下的后轴驱动力分配比λ与纵向加速度ax的关系。由于支架搬运车在空载和满载状态下前、后轴承载有较大区别,分别给出 2 种工况下的关系图,如图 2 所示。

图2 空载与满载工况下不同路面上的理想分配比Fig.2 Ideal distribution ratio on various road surface in no-load and full-load operation mode
从图 2 可以看出,在 2 种工况下,λ为 1 时,驱动力全部分配给后轮,随着加速度逐渐增加,载荷逐渐向前分配。图 2 中虚线表示在不同路面附着系数下车辆的纵向加速度的边界线,由于受到路面和轮胎的约束,所能达到的最大纵向加速度也必须在相应的范围内。
因此,在路面附着系数φ和整车纵向加速度ax已知的情况下,即可得出理想分配比λ。据此对车辆驱动力进行分配,在满足电动机驱动的约束条件下,前后轴附着率相等,左右车轮的驱动力平均分配。定义 4 个轮的前轴左侧轮胎、前轴右侧轮胎、后轴左侧轮胎和后轴右侧轮胎的垂直反力分别为Ffl、Ffr、Frl和Frr,有

1.2 转向工况的载荷分配
在直线行驶状态下,车辆左、右轮的垂直载荷大体上是相等的。但在转向行驶时,由于侧倾力矩的作用,在前、后车轴左、右车轮上的垂直载荷是不相等的。铰接式支架搬运车在转向时存在重心转移和离心力的作用,导致左右两侧的垂直载荷重新分配。以满载工况为例进行四轮载荷分析,建立车辆转向模型,如图 3 所示。Gf为前机架的重心,Gr为后机架的重心,为简化计算,假设在转向过程中后机架与x轴平行,O为前、后机架的铰接点,转向过程中前机架重心由Gf转移到′[7]。转向状态下的车辆简化模型如图 4 所示。

图3 满载工况下车辆转向模型Fig.3 Vehicle steering model in full-load operation mode

图4 转向状态下车辆简化模型Fig.4 Simplified vehicle model in steering mode
根据整车的转向几何运动关系,将转向角作为已知量,则 4 个车轮的转动半径分别为:
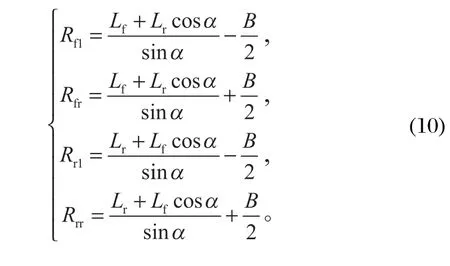
式中:Lf为前轴距铰接点O的垂直距离;Lr为后轴距铰接点O的垂直距离;α为铰接转向角;B为轮距。那么整车重心G′的位置为

式中:mf、mr分别为前、后机架的质量。
由于后轴与后机架采用回转轴承设计,因此转向状态下 2 个后轮的载荷


联立以上方程可得
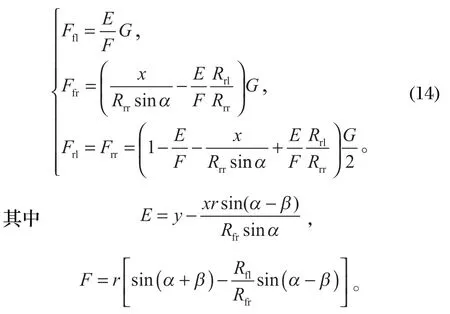
前、后轴侧向反作用力示意如图 5 所示。将作用在整车上的离心力Fsy的重心分配到前、后轴的重心上,并由前、后轴的侧向反作用力Fs1y、Fs2y平衡,即[9]:


图5 前、后轴侧向反作用力示意Fig.5 Sketch of lateral reaction force of front and rear axle
前、后车轮垂直反力的变动量如图 6 所示。将整车的前、后轴分开单独计算,即可求出左、右车轮垂直反力的变动量。


图6 前、后车轮垂直反力变动量示意Fig.6 Sketch of variation of vertical reaction force on front and rear wheels
作用在 4 个车轮上的垂直反力,是静止状态下的垂直反力与由离心力引起的垂直反力变动量之和,这个变动量在外侧车轮是增加垂直反力,而在内侧车轮则是减小垂直反力的。由此可知 4 个车轮的垂直反力的分配量为
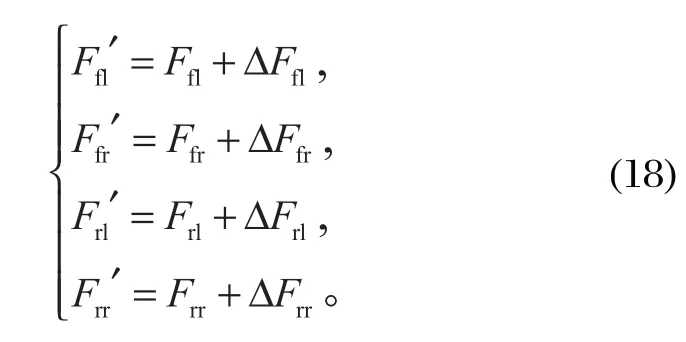
2 仿真分析
为了验证上述驱动力分配控制方式的可行性,联合使用动力学分析软件和数值分析软件对整车运动过程进行仿真和分析。在数值分析软件中对 4 个电动机及蓄电池支架搬运车整机进行建模,整机驱动模型如图 7 所示。

图7 整机驱动模型Fig.7 Vehicle drive model
由于在空载和满载 2 种工况下支架搬运车重心位置差别较大,因此分别对 2 种工况进行仿真分析[10]。对驱动力平均分配和理想分配的支架搬运车在平坦路面上空载和满载直线行驶工况下的加速度进行仿真,结果如图 8 所示。从图 8 可以看出,无论空载还是满载工况下,无论驱动力是平均分配还是理想分配,均获得一致的加速性能。

图8 空载和满载直线行驶工况下加速度变化曲线Fig.8 Variation curves of acceleration in no-load and fullload linear operating mode
对驱动力平均分配和理想分配的支架搬运车在满载爬坡工况下的爬坡角度进行仿真,结果如图 9 所示。从图 9 可以看出,驱动力理想分配的支架搬运车相比较平均分配可获得更大的爬坡角度。即在整车4 个电动机总输出转矩相同的情况下,理想分配后的车辆爬坡度最大可达 24% (爬坡角度 13.5°),相比较平均分配的爬坡度 20% (爬坡角度 11.3°),提高大约19%。

图9 满载爬坡工况下爬坡角度变化曲线Fig.9 Variation curves of climbing angle in full-load climbing mode
对驱动力理想分配的支架搬运车在空载和满载转向工况下的电动机输出转矩进行仿真,结果如图10、11 所示。从图 10、11 可以看出:车辆在经过0.5 s 转向后,4 个电动机的输出转矩逐渐达到平衡,空载转向时,由于整车后轴承载较大,后轴 2 个电动机的输出转矩均比前轴输出转矩大;整车向左转向,前、后轴左侧轮胎的承载增加,相应电动机的输出转矩比右侧电动机的输出转矩大。同理可知,满载向左转向过程中,前轴的承载较大,前轴左、右两侧的电动机输出转矩较后轴大,左侧电动机输出转矩比右侧电动机输出转矩大,达到预期的控制目标。

图10 理想分配的空载转向工况下电动机输出转矩变化曲线Fig.10 Variation curves of output torque of motors in no-load steering mode after ideal distribution

图11 理想分配的满载转向工况下电动机输出转矩变化曲线Fig.11 Variation curves of output torque of motors in full-load steering mode after ideal distribution
此外,对驱动力平均分配和理想分配的支架搬运车在空载和满载转向工况下的轮胎滑移率进行仿真,结果如图 12~ 15 所示。从图 12~ 15 可看出,为了保证整车具有较好的附着能力,经对驱动力重新分配控制后,车辆充分利用了垂直载荷较大的车轮的附着力,有效控制了垂直载荷较小的车轮的滑转,使车辆的转向稳定性在转向过程中有所增加,提高了整车综合性能。

图12 平均分配的空载转向工况下轮胎滑移率变化曲线Fig.12 Variation curves of slippage ratio of tyre in no-load steering mode after average distribution

图13 理想分配的空载转向工况下轮胎滑移率变化曲线Fig.13 Variation curves of slippage ratio of tyre in no-load steering mode after ideal distribution
3 试验
为了验证整车的性能,对整车进行爬坡和转向性能测试试验,如图 16 所示。通过对电动机输出转矩和电流进行理想分配控制后,车辆输出转矩明显优于平均分配的结果,实际测试中采用理想分配的车辆的最大爬坡度可达到 14°,采用平均分配的车辆的爬坡度低于 12°;转向响应时间由 7 s 缩短至 6 s,转向压力由 13.5 MPa 降低至 10 MPa,分别降低 12% 和26%,同时避免了转向过程后轮的打滑。

图16 支架搬运车性能测试试验Fig.16 Test for performance of bracket carrier
4 结语
针对四轮独立驱动电动支架搬运车 4 个电动机驱动力独立可控的特点,结合铰接式车辆的特点,分析了不同行驶工况下驱动力分配的控制算法,利用动力学分析软件和数值分析软件进行联合仿真,并对车辆进行跑合试验。仿真和试验结果均表明:独立控制 4 个轮边电动机的输出转矩后,车辆的爬坡性能提高,车辆转向稳定性提高,整车综合性能改善。

