考虑解列后孤网暂态稳定性的解列时刻实时决策方法

刘福锁，方勇杰，吴雪莲

（1. 华北电力大学电气与电子工程学院，北京市 102206；2. 智能电网保护和运行控制国家重点实验室，江苏省 南京市 211106；3. 国电南瑞科技股份有限公司，江苏省 南京市 211106）

0 引言

作为阻止电力系统失稳范围进一步扩大的系统性保护措施，失步解列必须考虑解列控制后分区电网能否保持暂态稳定运行能力［1-3］。传统失步解列控制对解列后孤网暂态稳定性问题的分析一般基于离线时域仿真，默认解列后孤网的同步稳定性与事前仿真分析结果相一致。实际工程中，选择在某一完整振荡周期结束后执行解列控制，而对于多套失步解列装置之间的配合问题，一般通过设置不同的失步振荡周期次数动作定值来获得装置动作时刻的选择性［4-5］。针对群内机组同调性较好的两群失稳模式，采用传统的失步解列控制，一般能满足解列后孤网机组保持同步稳定运行的要求［6］。已有多项研究成果表明，在复杂大电网中，系统失稳往往呈现群内非同调的特征，在完整振荡周期结束后执行解列控制，存在解列后孤网机组不能保持同步稳定运行的风险［7-9］，威胁大电网安全稳定运行。

一个完整的解列策略至少包括该不该解列、在哪里解列、何时解列等问题。其中，判断出系统失步且确定解列断面后在何时解列是其中复杂程度最高的问题［10］，已有研究成果不多。文献［11］论证了解列时刻是影响解列后孤网能否保持同步稳定运行的一个关键参量，为了保证解列后的孤网暂态稳定性，必须要对失步解列时刻进行约束。文献［12］基于不稳定平衡点定义了各个孤岛的临界能量，按照所有孤岛暂态能量都小于其临界能量的原则，提出了解列时刻离线整定方法。文献［13-14］从孤网机组动能累积的角度，认为尽快执行解列有利于孤网的暂态稳定性。文献［15］认为解列后孤网暂态稳定性的本质仍是大扰动下机组同步稳定性问题，取决于孤网群间总暂态能量（包括动能和势能）是否超过了其对应能量壁垒，从互补群群间暂态能量角度解释了不同解列时刻对孤网暂态稳定性的影响机理，揭示了解列后孤网暂态稳定性随解列时刻呈现非单调变化的规律，即并非越早解列效果越好。

在文献［15］的基础上，本文进一步针对考虑孤网暂态稳定约束的解列时刻实时决策难题，在假设可以无延时地获得系统运动轨迹的前提下，提出了基于解列后孤网暂态稳定性预估的解列时刻实时决策方法，以期为相关研究提供参考。

1 解列时刻精准判断解列后孤网暂态稳定性困难分析

1.1 观察区间受限导致无法精准判断孤网暂态稳定性

扩展等面积准则（EEAC）［16］通过互补群惯量中心-相对运动变换将多机受扰轨迹逐个时间断面映射到一系列聚合单机平面上，形成各单机映象系统的功率-转子角（P-δ）曲线。然后，用适当的面积严格量化各映象系统的稳定裕度，证明了多机系统失稳的充要条件是至少有一对互补群的群间相对动能超过了相应势能壁垒，也即对应的单机映象达到其P-δ平面上的动态鞍点（DSP）。

解列后构成孤网机组的运动轨迹，其互补群对应单机映象系统的运动方程如式（1）所示。

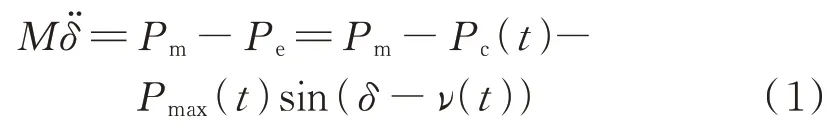
式中：M为等值惯量；δ为等值功角；Pm和Pe分别为等值机械功率和等值电磁功率；Pc(t)和ν(t)分别为等值功角特性中正弦电磁功率沿垂直方向和水平方向的偏移量；Pmax(t)为等值功角特性中正弦电功率的幅值。各参数计算方法详见文献［17］。

针对解列后的孤网，在互补分群的群内机组非同调时，单机映象的等值电磁功率含有时变参数，等值单机映象不是哈密顿系统。反映失稳机理的互补群群间能量不守恒，必须获得解列后孤网系统中多机实际受扰轨迹，才能对孤网的暂态稳定性做出精准判断［14］。而如果观察时刻止于解列时刻，即观察区间限于故障发生至解列时刻t的时段，则解列前的系统轨迹虽已形成，但解列后孤网系统的运动轨迹及其等值P-δ轨迹仍属未知。因此，只能在解列时刻采用解列后孤网群内机组同调的假设，对解列后孤网的等值P-δ轨迹及能量壁垒进行估算，进而得到解列后孤网暂态稳定裕度的估计值。

互补群的群内非同调性既可能有利于暂态稳定性，也可能不利于暂态稳定性［17］，而采用估算时的精度与解列后孤网群内机组非同调因素的强弱直接相关。

1.2 事前整定解列时刻难以保证解列后孤网的暂态稳定性

失步解列控制属于极端紧急状态下的安全稳定控制，是为保证电力系统承受第Ⅲ类大扰动时的安全要求而设置的控制措施，或作为系统因一些事先不可预计的各种偶然因素叠加而失去稳定后的对策［1-2］。在实际工程中，要想穷尽分析所有方式和故障下的电网失步振荡特性，并事前制定能保证解列后孤网暂态稳定的控制策略，几乎不可能实现。

此外，对于非自治电力系统，即使针对某一确定的失步振荡模式，不同方式不同故障下激发的振荡特征，以及解列后孤网的暂态稳定性也是千差万别。因此，难以通过事前计算找到影响解列后孤网暂态稳定性的关键状态量，并据此制定关于失步解列控制时刻的决策表，来保证解列后孤网同步稳定运行。

2 失步解列时刻实时决策中的关键因素

2.1 尽早启动解列时刻的实时决策流程

系统失步时刻指的是当等值两机系统间的功角差摆幅超过180°的时刻［1］。系统失稳时刻指的是至少有一对互补群的群间相对动能超过了相应的势能壁垒，也即对应的单机映象越过其P-δ平面上DSP的时刻［14］。

在解列后孤网为理想两群振荡模式下，式（1）中的Pc(t)、Pmax(t)、ν(t)变为不含t变量的固定常数，分 别 用Pc、Pmax和ν表 示，其 单 机 映 象 的P-δ轨 迹 如附录A 图A1 所示，图中，Pe为在垂直方向偏移Pc、水平方向偏移ν的关于功角δ的正弦曲线。以解列后孤网的正向摆动为例，在经典模型下，正向摆动DSP 的对应功角δDSP为：

在实际电网的多数场景下，多机系统互补群单机映象中Pm＞Pc，δDSP通常小于180°，利用单机映象穿越DSP 判断系统失稳的时刻，往往早于判断出失步的时刻，文献［18］介绍了具体案例。

因此，考虑为解列时刻的实时决策提供尽可能大的可用时长，有必要将原多机系统的失稳判据和失步判据均作为解列时刻实时决策的启动判据，即满足系统失稳和失步中任一判断条件，就触发决策流程。

2.2 保证解列后孤网的暂态稳定性

在解列时刻，采用文献［15］在解列后孤网单机映象P-δ平面上构建的能量壁垒Esb和暂态能量函数E的差值，计算解列后孤网的暂态稳定性，如式（3）所示。Ep＞0 表示解列后孤网暂态稳定，Ep＜0表示解列后孤网暂态失稳，Ep=0 表示解列后孤网临界稳定。

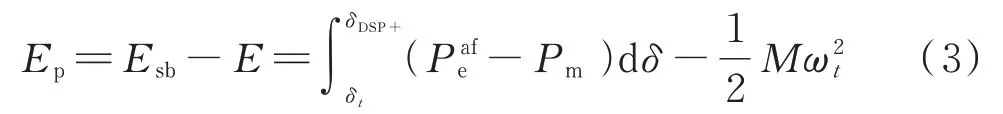
执行解列操作后，通常形成2 个或多个孤网。为了对解列后不同孤网的暂态稳定性进行对比分析，利用解列后孤网单机映象能量壁垒Esb对稳定裕度作标幺化处理，得到如式（4）所示的解列后孤网在正向摆次运动中的暂态稳定裕度η+。

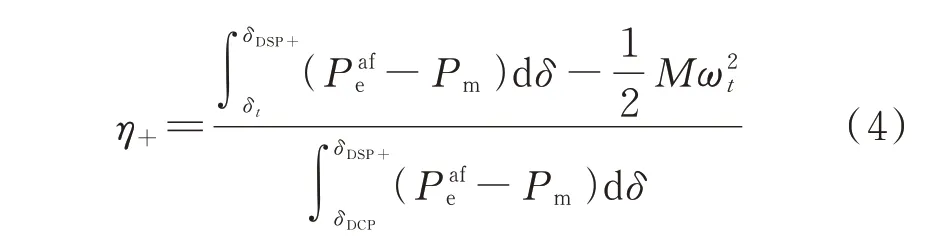
式中：δDCP为等值单机映象动态中心点（DCP）处功角。

同理，对于反向摆动，可得到解列后孤网暂态稳定裕度η-如式（5）所示。

式中：δDSP-为等值映象运动轨迹的反向摆动中DSP处的功角。

综上，对于某一确定孤网，取解列后孤网等值映象运动轨迹中正向摆动和反向摆动的稳定裕度最小值为其暂态稳定裕度，如式（6）所示。

需要说明的是，通过式（4）至式（6）计算得到的孤网暂态稳定裕度，是在解列时刻冻结孤网内非自治因素，按照解列后孤网群内机组同调假设得到的结果。为了保守起见，可设置一个暂态稳定裕度阈值ε，将η＞ε作为解列后保证孤网暂态稳定的约束条件。

2.3 判断延迟解列对孤网暂态稳定性的影响

由文献［15］可知，尽快解列不一定有利于解列后孤网的暂态稳定性，解列后孤网暂态稳定性随解列时刻的变化往往呈现出非单调的变化规律。也即，如果延迟解列能提高解列后孤网的暂态稳定性，在系统对失步振荡持续时间的可接受范围内，就没必要尽快执行解列。

在解列后孤网为理想两群振荡假设下，解列后孤网暂态稳定裕度随解列控制时刻变化的灵敏度指标α(t)如式（7）所示［15］。

式（7）本质是反映孤网群间暂态能量随解列时刻的变化规律，α(t)＞0 时，表明延迟解列，孤网群间暂态能量将降低，延迟解列有利于提高孤网暂态稳定性。对于延迟解列是否有利于孤网暂态稳定性的判断，无须对α(t)求解精确的数值解，采用其符号即可判别解列时刻对孤网暂态稳定性影响的趋势。

由于孤网能量壁垒Esb为一正数，不影响对α(t)的符号判断，可以将式（7）做进一步简化，得到孤网暂态稳定性随解列时刻变化的趋势指标β(t)。

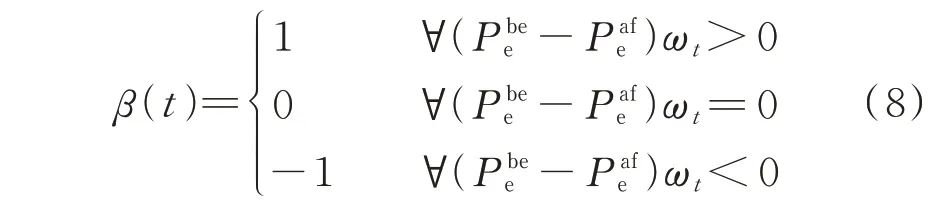
当β(t)=1 时，延迟解列有利于孤网暂态稳定性；当β(t)=-1 时，延迟解列不利于孤网暂态稳定性；β(t)=0，表示该时刻对应解列后孤网稳定裕度的极值点或拐点，延迟解列对解列后孤网暂态稳定性影响不确定。

在失步振荡过程中，常常会伴随着机组频率或机端电压的异常变化。实际系统中的大部分机组从保护本体的角度，配置了高频、低频、高低压保护装置。从系统安全角度，部分机组还配置了高频切机等功能。在失步振荡引发机组运行频率/电压超过限值时，相关保护的动作会导致机组紧急停机，因此有必要在机组运行参数越限之前进行解列控制，尽可能避免大量机组无序脱网可能导致的连锁反应，减小控制代价。

其次，根据电网的可承受能力或多解列装置间协调配合的要求，离线整定各个失步解列装置的解列动作时刻定值（通常为整数倍的失步振荡周期）。

因此，针对确定的失步解列断面，失步振荡持续时间的可接受性体现在两个方面：一是机组运行参数在可接受的范围内；二是失步振荡时间小于离线整定的解列时刻动作定值。例如，只关注机组频率时，该约束在数学上可描述为：

式中：f为机组频率的实测值；fmin和fmax分别为机组频率的下限和上限；δd为等值两机系统功角差；n为离线整定的解列控制时间对应的失步振荡周期数。

3 失步解列时刻的实时决策方法

3.1 失步解列时刻实时决策问题的分解

本文将解列时刻实时决策问题分为失步振荡的允许持续时间判断、解列后暂态稳定裕度最小的孤网识别和解列后孤网暂态稳定裕度局部极大值出现时刻判别等3 个子问题。

1）失步振荡的允许持续时间判断

当机组频率实测值已超过整定的范围或者失步振荡时间已达到离线整定的解列动作周期数时，应立即执行解列控制。当原多机系统失步和失稳条件均满足时，估算的孤网暂态稳定裕度小于设定阈值，且延迟解列不利于孤网暂态稳定性的提高时，应立即执行解列控制。

式（10）综合了需要立即执行解列控制的判断条件，3 个条件之间为“或”逻辑关系。其中，ε、fmax和fmin需要根据电网的实际情况进行整定。

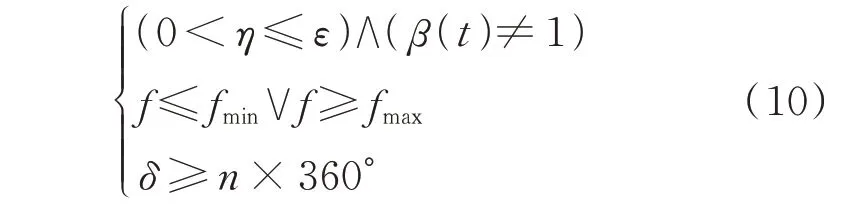
2）解列后暂态稳定裕度最小的孤网识别

失步解列控制动作后将形成两个或多个孤网，解列控制需要考虑解列后每个孤网的暂态稳定性，其中，解列后暂态稳定裕度最小的孤网的稳定水平是决定失步解列时刻的关键。因此，在解列时刻决策过程中，应根据式（4）至式（6）对每个孤网的暂态稳定性进行量化评估，识别并选择暂态稳定裕度最小的孤网作为关注对象。由于每个孤网暂态稳定裕度的时变性，需要对该识别结果进行动态跟踪和更新。

3）解列后孤网暂态稳定裕度局部极大值出现时刻判别

对解列时刻进行实时决策，要求在解列后系统运动轨迹未知的情况下，就要判断是否应该执行解列。因此，在决策时间有限的情况下，只能根据已有信息和短时预测信息，捕捉组成孤网的子系统在解列前群间暂态能量出现局部极小值，即解列后孤网暂态稳定裕度出现局部极大值的时刻，在该时刻解列，有利于提高解列后孤网的暂态稳定性。

根据β(t)与解列后孤网暂态稳定性的关系可知，在解列后孤网为理想两群振荡模式的假设下，暂态稳定裕度极大值出现的特征为：前一时刻的β(t)即β(t-1)等于1，当前时刻的β(t)等于0，下一时刻的β(t)即β(t+1)等于-1。

式（11）列出了孤网暂态稳定裕度极大值出现时刻的2 个判断条件，其中第1 个条件考虑了因采样步长过大而未监测到极大值的情况，与第2 个条件为“或”逻辑关系。

3.2 失步解列时刻实时决策的流程

失步解列时刻实时决策流程如图1 所示。

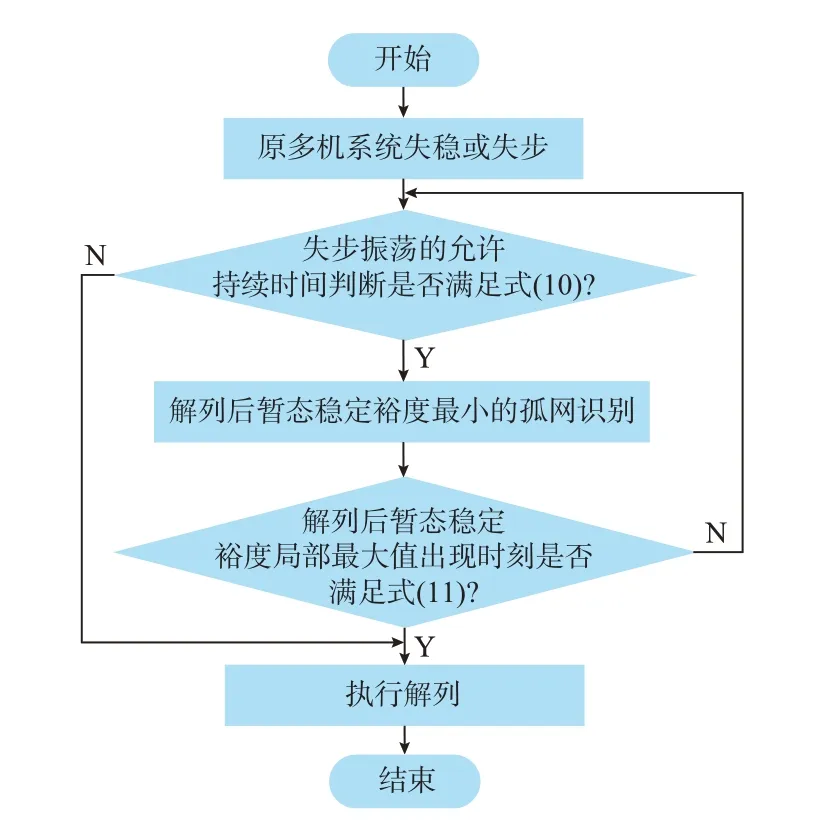
图1 考虑解列后孤网暂态稳定性的解列时刻决策流程Fig.1 Decision-making process of splitting time considering transient stability of isolated power grid after splitting

步骤1：对原多机系统暂态稳定性进行实时判断。当判断出原多机系统失稳或失步时，启动解列动作时刻决策流程。

步骤2：实时量测机组频率和功角等信息，计算不同孤网暂态稳定性随解列时刻变化的趋势指标。判断式（10）中任一条件是否满足，如任一条件满足，表示已达到失步振荡的允许持续时间，立即执行解列控制；如不满足，执行步骤3。

步骤3：利用式（4）至式（6）对在当前时刻执行解列后，所形成的每个孤网的暂态稳定性进行量化评估，识别并选择暂态稳定裕度最小的孤网，进入步骤4。

步骤4：针对步骤3 选择的暂态稳定裕度最小的孤网，计算暂态稳定性随解列时刻变化的趋势指标。判断式（11）中任一条件是否满足，如任一条件满足，表明该孤网暂态稳定裕度出现局部极大值，触发执行解列控制；如不满足，返回步骤2。

4 算例分析

4.1 解列后孤网群内机组同调的算例

采用附录B 图B1 和表B1、表B2 所示的3 机9节点系统，验证本文提出的解列时刻实时决策方法。设定暂态稳定阈值ε=5%，并假设不考虑其他约束条件。

0 s 时，BUS5-BUS7 线路发生三相永久性N-1故障，0.26 s 时切除故障线路，机组功角响应曲线如附录B 图B2 所示，G2-G3 机组构成领先群相对G1机组发生失步振荡。0.45 s 单机映像轨迹穿越DSP，系统失稳，0.75 s 两群相对功角摆开180°，系统失步，1.02 s 时两群相对功角摆开360°，达到一个失步周期。解列前机群G2-G3 和解列后所构成孤网的等值单机映象如图2 所示。按照式（4）至式（6）计算得到的裕度指标，以及按照式（8）计算得到的孤网暂态稳定性随解列时刻变化的趋势指标见图3。

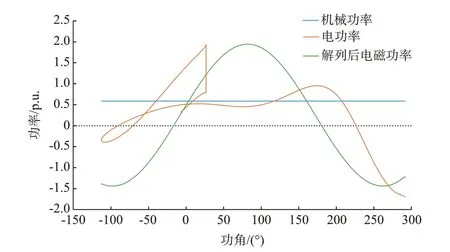
图2 G2-G3 机群等值功角响应及解列前后P-δ 等值曲线Fig.2 Equivalent power angle response of generator cluster G2-G3 and P-δ curves before and after splitting

图3 孤网暂态稳定性随解列时刻变化的趋势指标Fig.3 Trend index of transient stability of isolated power grid varying with splitting time

可见，本算例中解列后G2-G3 所构成孤网在解列后能保持暂态稳定的解列时刻区间为0.57～0.80 s。如果按照传统失步解列控制方法，在一个失步周期（本算例对应1.02 s）执行解列，解列后G2-G3 机组构成孤网暂态失稳，稳定裕度为-24.05%。

根据3.2 节描述的解列时刻实时决策方法，在0.45 s 启动决策流程。根据图3 所示的计算结果可知：β(0.69 s)=1，β(0.70 s)=-1，即在0.70 s 满足式（11）的判断条件，触发解列控制，解列后孤网暂态稳定裕度为70.87%，对应一个局部极大值。这表明，本文方法能在保证解列后孤网暂态稳定的前提下，尽量提高解列后孤网的暂态稳定裕度。

4.2 解列后孤网群内机组不同调的算例

采用如附录C 图C1 所示10 机39 节点系统（参数设置见附录C 表C1、表C2），进一步验证本文提出的解列时刻实时决策方法。设定暂态稳定阈值ε=5%，并假设不考虑其他约束条件。

0 s 时，BUS16-BUS17 线路发生三相永久性N-1 故障，0.15 s 时切除故障线路，机组功角响应曲线如图4 所示，G33-G36 机组构成领先群相对其他机组发生失步振荡，领先群和余下群内机组均呈现非完全同调现象。

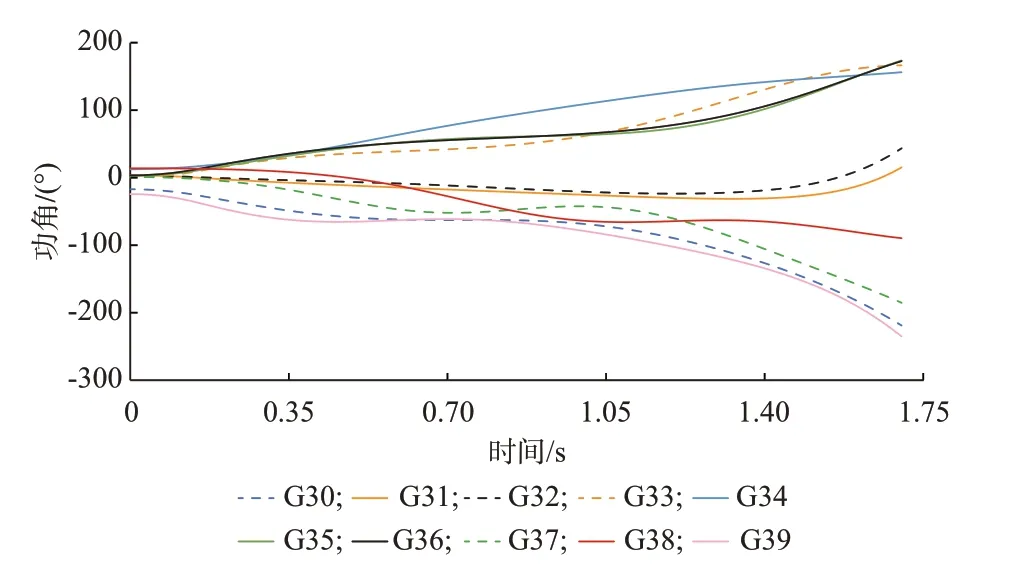
图4 机组的功角响应曲线Fig.4 Power angle response curves of units

该分群模式下的原10 机系统等值单机映象详见附录C 图C2。故障后0.77 s 系统暂态失稳，故障后1.32 s 两群相对功角摆开至180°，系统失步。在该失步振荡模式下，振荡中心落在线路BUS14-BUS15 上。根据决策流程，0.77 s 启动解列时刻的实时决策。

定义解列后G33-G36 机组构成的孤网为孤网A，G30-G32 和G37-G39 机组构成的孤网为孤网B。

由于孤网A 内机组同调性较好，在任何时刻执行解列后其暂态稳定裕度均大于孤网B，即孤网B为暂态稳定裕度最小的孤网。

孤网B 内的主导分群模式存在时变，0.76～1.18 s 为G38 机组相对其他机组振荡，1.18 s 后演化为G31-G32 机组构成领先群，相对其他机组振荡。对于G38 机组相对其他机组振荡的分群模式，在1.18 s 解列时，解列前机群B 和解列后孤网B 的等值单机映象详见附录C 图C3。对于G31-G32 机组相对其他机组振荡的分群模式，在1.32 s 解列时，解列前机群B 和解列后孤网B 的等值单机映象详见附录C 图C4。

根据图C3 和图C4，按照式（4）至式（6）计算得到裕度指标，同时按照式（8）计算得到孤网B 暂态稳定性随解列时刻变化的趋势指标。为便于比较，在根据本文方法计算稳定裕度的同时，基于时域仿真结果，获得解列后系统运动轨迹，再计算不同时刻执行解列控制时孤网的暂态稳定裕度，计算结果如图5 所示。

图5 孤网B 暂态稳定裕度和趋势指标Fig.5 Transient stability margin and trend index of isolated power grid B

分析计算结果有以下结论：

1）按照传统解列控制方法，在一个完整的失步周期执行解列，解列后孤网B 暂态失稳。即使将执行解列的时刻提前到系统失步时刻（本算例对应1.32 s），解列后孤网B 仍存在暂态失稳问题。

2）采用本文方法，1.19 s 时满足式（11），因而在1.19 s 触发解列控制，解列后孤网暂态稳定裕度为34.5%，这是采用解列后孤网群内同调假设的估算结果。采用了全动态过程的时域仿真轨迹计算孤网暂态安全稳定裕度时，考虑了群内机组非同调的影响。在1.19 s 执行解列控制时，解列后孤网的暂态稳定裕度为58.96%。与上述采用解列后孤网群内同调假设的估算结果存在一定的偏差。

为应对由于不能考虑解列后群内机组非同调的影响而产生的偏差，本文通过设置一个稳定裕度阈值，作为在解列时刻进行实时决策时对估算的稳定裕度的约束。

5 结语

本文对考虑解列后孤网暂态稳定性的失步解列时刻的实时决策方法进行了如下探索性研究：

1）在对解列时刻进行实时决策时，由于无法获得解列后机组的运动轨迹信息，因而无法保证能在解列时刻对解列后孤网的暂态稳定性做出精准的定量分析，但仍有根据解列前系统的运动轨迹信息和预估信息进行决策的可行性。

2）对于解列后孤网的运动为理想两群振荡模式的情况，可利用孤网暂态稳定性随解列时刻变化的趋势指标，来捕捉解列后孤网暂态稳定裕度局部极大值的出现时刻，从而在可接受的失步振荡持续时间范围内，通过延时解列来提高解列后孤网的暂态稳定性。

3）对于解列后孤网的运动为非理想两群振荡模式的情况，基于解列后孤网群内同调假设的暂态稳定裕度估算结果，会与实际情况存在一定偏差，可通过设置稳定裕度阈值的方法来增强基于预估结果进行决策的保守性。

本文方法如果应用于工程实践，即使具有统一时标的全网信息的获取不再是技术瓶颈，也必须考虑信息的测量、传输、处理的总时延所产生的影响。如何考虑延时和解列后非同调对本文方法的影响，需要进一步开展深入研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。