含串补及STATCOM 的交直流系统稳定性分析及改善方法
夏海涛,周小平,刘一锋,洪乐荣,罗 安
(国家电能变换与控制工程技术研究中心(湖南大学),湖南省 长沙市 410082)
0 引言
近年来,基于电网换相换流器的高压直流(linecommutated converter based high voltage direct current,LCC-HVDC)输电技术在远距离大容量输电领域广泛应用,为促进中国东西部地区经济和资源的协调均衡发展起到了重要作用[1-2]。然而,当LCC-HVDC 馈入弱受端电网时,其在过电压水平、换相失败抵御能力、直流输电能力等暂稳态性能方面将面临严峻挑战。为了改善弱受端LCC-HVDC系统运行特性,在受端母线出线上安装串补电容及在换流站安装静止同步补偿器(static synchronous compensator,STATCOM)是较为经济有效的措施[3-4]。然而,实际工程的运行经验显示,投运串补或STATCOM 也可能在受端引发谐振失稳现象[5-6]。这种由受端附加装置导致的次生稳定性问题会造成滤波设备跳闸及直流降功率运行,威胁到受端交直流电网的安全稳定运行,亟须解决。因此,国内外学者对此进行了较为深入的研究。
文献[5]报道并分析了永富直流工程富宁站出现的谐振长时间不衰减现象。该文献通过扫频的方式测量了富宁站的输出交流阻抗,认为直流输电系统与串补线路之间存在的低频串联谐振是上述不稳定现象的主要诱因。文献[6]则详细分析了换流器调制特性与变压器饱和特性之间的相互作用机理,并测量了考虑变压器饱和特性后的换流站交直流阻抗。结果显示,变压器的饱和特性会进一步降低系统稳定裕度。文献[5-6]揭示了永富直流与受端串补之间的相互作用机理,但其研究忽略了STATCOM 的影响,而后者也已应用于实际工程[7]。
在STATCOM 对LCC-HVDC 系统小信号稳定性的影响方面,文献[8]建立了STATCOM 序阻抗模型并指出其会减小系统在谐振点处的等效电阻;而文献[9]则发现STATCOM 交流电压外环与电网换相换流器(line-commutated converter,LCC)锁相环之间的耦合作用会降低系统稳定裕度。但上述文献没有研究串补电容及STATCOM 并联数目的影响。在实际工程中,为了提供足够的动态无功支撑,一般会在逆变站安装多台STATCOM[7]。而对于邻近地区含有多台STATCOM 的电网而言,随着STATCOM 并联台数的增加,其发生小信号失稳的风险也会增加[10]。针对永富直流工程受端出现的振荡问题,文献[11]研究了串补电容、短路比及STATCOM 并联台数等因素影响,并认为短路比及STATCOM 并联台数是导致LCC-HVDC 系统振荡的主要原因。然而该文献主要通过仿真扫描法进行研究,没有建立适用于稳定性分析的解析模型,因而未能充分揭示串补及STATCOM 对受端交直流系统阻尼、振荡模态的影响和相应的机理。
综上所述,对于高压直流输电系统中由受端附加装置引发的不稳定性问题,业界已取得了有价值的研究成果,但现有文献仍存在被研究主体考虑不全面、对串补及STATCOM 的影响及其机理揭示不充分等不足。鉴于此,本文首先给出了受端含串补电容及STATCOM 的LCC-HVDC 系统结构化小信号模型;然后,基于此模型分析了串补电容、STATCOM 及其并联台数对系统主导极点轨迹的影响,并给出了相应的机理解释;接着,为了减小串补电容的负面影响和改善多台STATCOM 运行的稳定性,提出了触发角指令反馈控制及有功电流补偿控制;然后,通过PSCAD/EMTDC 电磁暂态仿真模型验证了模型分析的正确性和所提方法的有效性;最后,比较了逆变站控制模式对混合系统稳定性影响的差异。
1 受端含串补及多台STATCOM 的LCCHVDC 系统小信号模型
受端含串补及多台STATCOM 的LCC-HVDC系统(以下简称“混合系统”)的结构如图1 所示,该系统的额定电压为500 kV,额定功率为1 000 MW。图1 中:下标“i”和“r”分别代表逆变侧和整流侧变量;V̇表示换流母线相电压;id和İ分别表示直流电流和变换器输出交流电流相量;ud表示直流电压;Ls表示平波电抗器;Pd表示流入(流出)平波电抗器的直流功率;P和Q分别表示变换器输出的有功和无功功率;E表示交流电压源幅值;Rd为直流线路电阻,Cd为直流线路等效直流电容;kT为换流变压器变比;R1r、R2r为送端电网电阻,L1r为送端电网电感;Ri和Li分别为受端电网电阻和电感,Ci为串补电容;STATCOM 通过升压变压器接入换流母线,kst为升压变压器变比;vsp为STATCOM采样交流三相电压;ist和ists分别为STATCOM 并网变压器原、副边侧输出交流三相电流;vst为STATCOM 输出交流三相电压;udc和idc分别为直流电压和直流电流;Cst为直流侧电容。
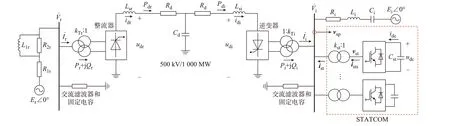
图1 混合系统主电路Fig.1 Main circuit of hybrid system
混合系统的控制系统如附录A 图A1 所示。图A1(a)为LCC-HVDC 控制系统示意图,其中,整流侧为定直流电流控制而逆变侧为定关断角控制。STATCOM 外环采用的是定直流电压/定交流电压控制而内环为定电流控制,如图A1(b)所示。
1.1 LCC-HVDC 小信号模型
LCC-HVDC 的结构化小信号模型如图2 中左侧框图所示。参照文献[12]给出的LCC-HVDC 整流站线性化模型的推导过程,不难得到逆变站的小信号模型。因此,本文对LCC-HVDC 的建模过程不再赘述。图2 中:“Δ”表示对应变量的小扰动量;下标“0”表示稳态值;Lpfγ为定关断角控制的低通滤波器;ΔθIi和ΔIi分别为逆变器输出交流电流的相位和幅值;Δφi为逆变器功率因数角;ΔVi为相电压幅值;Δγ和Δαoi分别为关断角及逆变器触发角指令,而 系 数kαoγ体 现 了 Δαoi对 Δγ的 影 响,且 有kαoγ=kδγ=-sinαi0/sinγ0(αi和γ分别为触发角和关断角);Δδi为LCC 锁相环跟踪误差;PIplli和PIγ分别为LCC 锁相环和定关断角控制的比例-积分(PI)控制器;Ldi为考虑了变压器漏抗的等效直流电抗;传递函数Gdcr(s)则代表直流线路、整流站及其交流系统的动态特性。图2 中其他系数的表达式详见附录A 式(A1)—式(A7)。

图2 混合系统结构化小信号模型Fig.2 Structured small-signal model of hybrid system
1.2 STATCOM 小信号模型
STATCOM 的输出阻抗及小信号稳定性主要受其交流电压环影响[13],而交流电压环控制带宽通常远小于电流内环的控制带宽[14]。因此,本文将主要关注STATCOM 电压外环控制时间尺度内[15]的稳定性问题,并认为STATCOM 输出电流等于外环输出的电流指令。于是,容易得到STATCOM的结构化小信号模型,如图2 中右侧框图所示,其中:Δvi,d、Δvi,q和 Δist,dn、Δist,qn分 别 为 第n台STATCOM 的d、q轴输入电压和输出电流;矩阵Yst为STATCOM 在dq坐标系下的输出导纳矩阵,其表达式详见附录A 式(A8)—式(A13)。
1.3 受端交流系统模型
受端交流系统模型(含交流滤波器及固定电容)可用一多输入多输出传递函数Jgi(s)表示。Jgi表征了LCC 和STATCOM 输出到它们的输入之间的交互作用及动态特性,即有:

式中:ygi、ugi分别为受端交流系统的输出和输入向量;ygLi=[ΔPi,ΔQi]T和ygstn=[Δvi,d,Δvi,q]T分 别 为交流系统到LCC 和第n台STATCOM 的输出;uLi=[ΔθIi,ΔIi]T和ustn=[Δist,dn,Δist,qn]T分别为LCC和第n台STATCOM 给交流系统的输入。
Jgi的表达式为:
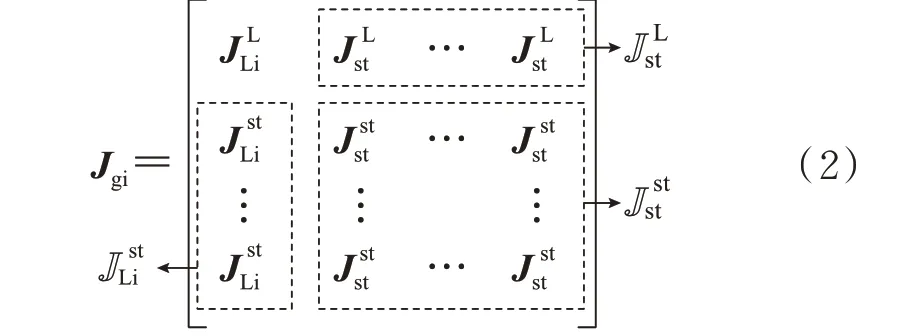
1.4 模型验证
为了验证混合系统结构化小信号模型的可行性,下面将比较其与PSCAD/EMTDC 中的电磁暂态模型的阶跃响应。混合系统的部分参数如附录A表A1 所示。在实际工程中,当电容集中安装在线路中点时,超高压远距离输电线路的串补度一般不超50%[16]。考虑到一定的调节余量,本文按37%的串补度选取串补电容值。此外,由于串补电容提供了部分无功功率,为了使换流母线电压维持在额定值附近,换流站固定电容器容值修改为2.52 μF。LCC 其余参数与CIGRE 标准模型相同[12]。
当LCC 关断角指令γref和STATCOM 交流电压指令vd,ref分别阶跃1°和0.01 p.u.时,混合系统响应曲线分别如附录A 图A2(a)和(b)所示。图A2 中小信号模型与电磁暂态模型的阶跃响应基本一致,验证了小信号模型的可行性。
2 串补及STATCOM 对受端交直流系统小信号稳定性的影响
2.1 混合系统的闭环传递函数
把STATCOM 看作交流系统的一部分,可以推得小信号模型的整合形式,如附录B 图B1(a)所示。图B1(a)中,GPθi(s)和GQθi(s)分别表示ΔPi和ΔQi对ΔθIi的影响,Giθi(s)表示Δidi对ΔθIi的影响,它们的表达式见附录A 式(A4)—式(A6);而和则分别表征了受端交流系统和STATCOM 对LCC的影响,其中的表达式为:

式 中:Yst=diag{Yst,…,Yst};为STATCOM 输出到LCC 输入之间的传递函数矩阵;为STATCOM 输出到STATCOM 输入之间的传递函数矩阵;为LCC 输出到STATCOM 输入之间的传递函数矩阵;I为2×2 的单位矩阵。
如果把假想功率ΔPv看作系统输入,直流电流Δidi看作系统输出,则由附录B 图B1(a)可进一步得到混合系统的单输入单输出形式,如图B1(b)所示。图B1(b)中,Hfb(s)为反馈传递函数,其表达式为:

由自动控制原理可知,系统闭环传递函数的主导极点在复平面的位置决定了系统的稳定性。因此,以下将利用Φhvdc(s)的主导极点轨迹来分析串补及STATCOM 对混合系统稳定性的影响。
2.2 串补及单台STATCOM 的影响
令LCC 定关断角控制器比例系数kpγ从0.2 变化到1.4,则可得到混合系统在无附加装置、只投入串补、投入串补及1 台STATCOM 这3 种场景下的主导极点轨迹,如图3(a)所示。业界对电力系统振荡频率的划分标准如附录B 表B1 所示[17]。为方便起见,本文根据虚部大小将图3 中的主导极点划分为低频主导极点p1,2(10 Hz 左右,dq坐标系)、中频主导极点p5,6(48 Hz 左右,dq坐标系)和高频主导极点p3,4(120 Hz 左右,dq坐标系)。
比较图3(a)中的玫红色轨迹和蓝色轨迹之间的差异后可以看出,投入串补电容后,混合系统低频主导极点p1,2和高频主导极点p3,4整体移到了左半平面内,并且增加了一对中频主导极点p5,6。对比kpγ在这2 种场景下使系统保持稳定的临界值:投入串补后系统kpγ的临界值约为0.3(p5,6),小于不含串补时的临界值1.0(p3,4)。这意味着投入串补电容虽然能改善高压直流输电系统的低频和高频稳定性,但增加的中频主导极点降低了系统整体的稳定裕度。即从整体上说,投入串补会削弱受端交直流系统的稳定性。在投入1 台STATCOM 后,混合系统的主导极点轨迹如图3(a)中绿色轨迹所示。从绿色主导极点轨迹可以看出,在投入STATCOM 后,p5,6整体向左半平面移动,并且kpγ的临界值提高到了0.5左右。对于p1,2、p3,4而言,它们也仍然保持在左半平面内。该结果表明,投入单台STATCOM 能减小串补电容对系统中频稳定性的负面影响,而对系统低高频稳定性的影响较小。
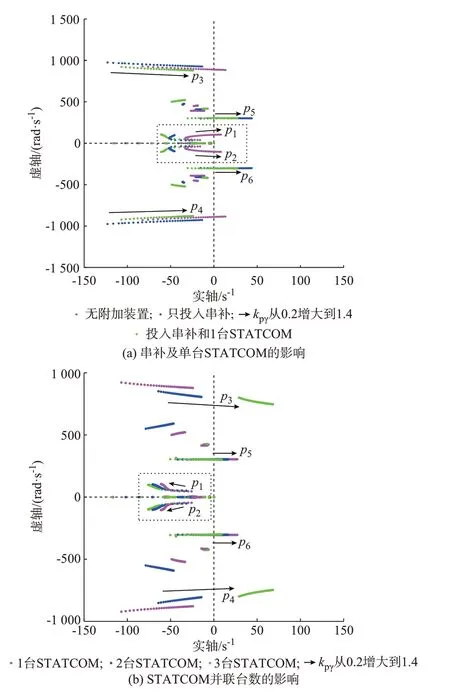
图3 串补及STATCOM 对混合系统主导极点的影响Fig.3 Impacts of series compensation and STATCOM on dominant poles of hybrid system
2.3 STATCOM 并联台数的影响
当换流站并联多台STATCOM 运行时,混合系统中LCC 与STATCOM 的交互作用媒介不仅有交流电网,还包括其他STATCOM。因而多台STATCOM 并联运行对系统的影响可能有别于单台STATCOM 的影响。 因此,以下着重分析STATCOM 并联台数对系统稳定性的影响。
图3(b)展 示 了 逆 变 站 分 别 投 运1 至3 台STATCOM 时混合系统的主导极点轨迹。比较图3(b)中3 条轨迹的相对位置可知,随着STATCOM投运数量的增加,p5,6向左半平面移动而p3,4则明显向右半平面移动。该结果表明,投运更多的STATCOM 有利于混合系统中频稳定性,但会恶化系统高频稳定性。特别的,对于本文所给工况,当逆变站投运3 台STATCOM 时,高频主导极点轨迹完全位于右半平面内,混合系统失稳。
3 串补和多台STATCOM 运行降低系统稳定性的机理解释
主导极点轨迹虽然能显示系统的主要振荡模态,但缺少直观的物理解释。为此,本章将分别从LCC 定关断角控制特性和频率阻抗(导纳)这2 个角度来解释串补和STATCOM 运行台数增加导致的LCC-HVDC 系统受端不稳定现象。
3.1 控制灵敏度传递函数
文献[18]提出了控制灵敏度指标(control sensitivity index,CSI)来评估LCC-HVDC 系统的静态稳定性。CSI 的数学实质是在系统的基频稳态条件下,控制器输入变量对输出变量的偏导数,其中输出变量为控制量而输入变量为被控量。以定关断角控制为例,CSIγ=(∂γ/∂α)|X0(X0表示稳态点)。对于定关断角控制方式而言,当γ因扰动而偏离其指令值时(不妨假设偏大),那么αoi在控制器PIγ的作用下会变大。经过系统响应后,如果αoi的增大能使γ减小,即CSIγ小于0,那么定关断角控制能实现“正调”,系统关于γ形成负反馈,关断角跟踪误差在“正调”的作用下逐渐减小,系统稳定;反之,则系统不稳定。因 此,CSIγ的 物 理 含 义 是LCC-HVDC 系 统 在稳态条件下能实现定关断角控制“正调”的程度。CSIγ描述了系统触发角指令到关断角的静态响应特征,具有易于理解的物理意义。不足的是,CSIγ没有包含LCC-HVDC 系统在其他频率处的稳定性信息。鉴于此,本文将CSIγ这一概念扩展到全频域,得到关于定关断角控制的控制灵敏度传递函数:
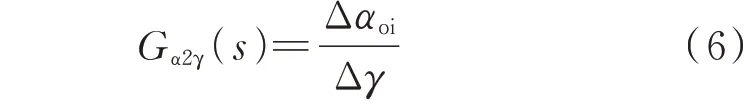
利用Gα2γ(s)的频率响应和正负反馈的概念可定性分析LCC-HVDC 系统受端的小信号稳定性。本文主要探究受端的小信号稳定性问题,所以为了降低Gα2γ(s)的阶数,在下文基于扩展CSIγ概念的分析中暂不考虑送端的影响,即令图2 中的Gdcr(s)=0。
3.2 串补电容失稳机理
1)从定关断角控制特性的角度分析
在小信号模型的Δγ和Δαoi两处分别设置断口,可得到传递函数Gα2γ(s)的示意图,如附录B 图B2 所示。Gα2γ(s)可拆分为直接传递系数kαoγ和间接传递函 数G'α2γ(s)两 部 分。kαoγ代 表Δαoi对Δγ的 直 接 影响。此外,Δαoi会通过主电路和控制电路的交互作用影响系统的电压/电流等电气量,进而影响Δγ。G'α2γ(s) 则 反 映 了 这 种Δαoi对Δγ的 间 接 影 响。Gα2γ(s)的频率特性如图4 所示。
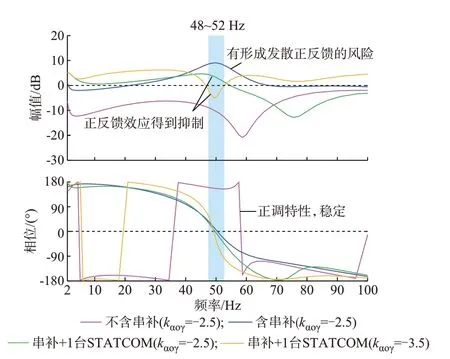
图4 Gα2γ(s)的频率响应曲线Fig.4 Frequency response curves of Gα2γ(s)
当受端不含串补时,Gα2γ(s)的相位∠Gα2γ(jω)在±180°附近,Δαoi与Δγ近似反相,这表明定关断角控制为“正调”,对Δγ形成负反馈,系统稳定,如图4中玫红色曲线所示。受端加入串补后,∠Gα2γ(jω)在中频段附近穿过0°,Δαoi与Δγ同相,这意味着定关断角控制存在“反调”并对Δγ形成正反馈,如图4 中蓝色曲线所示。此外,中频处相应的幅值|Gα2γ(jω)|接近10 dB,Δαoi到Δγ的响应大幅同相放大。因此,定关断角控制在该频率附近有对Δγ形成发散正反馈的风险。蓝色和玫红色曲线的对比表明,串补的投入使得定关断角控制特性在中频附近由“正调”变为“反调”,大幅增加了关断角形成发散正反馈的风险,从而降低了系统在中频段的稳定性(dq坐标系下的中频)。图4 中绿色曲线显示,在含串补的受端系统投入1 台STATCOM 后,|Gα2γ(jω)|在中频附近从10 dB 衰减到5 dB。这表明STATCOM 能改善系统中频段的关断角控制特性,削弱形成发散正反馈的条件,从而增强系统在中频段的稳定性。
因此,从定关断角控制特性的角度看,串补降低系统中频稳定性的机理为:串补使得LCC 定关断角控制的中频特性由“正调”变成了“反调”,让受端交直流系统形成了关于关断角的正反馈。
2)从频域阻抗的角度分析
附录B 图B3(b)对比了投入串补前后abc 坐标系下的交流系统阻抗Zaci(s)的频率响应曲线。从图B3(b)可以看出,投入串补后,Zaci从强阻弱感性变为弱阻强容性。图B3(c)给出了稳定条件下LCC 交流阻抗的扫频测量值ZLCC。从ZLCC的频率响应曲线可知,其在低频段(<10 Hz)的相位在60°左右,表明LCC 交流阻抗呈阻感特性。因此,高压直流输电系统如果因运行参数变化而使其逆变侧交流阻抗在低频段呈负阻强感性,则会与交流系统形成发散的低频串联谐振(对应于上文dq坐标系下的中频振荡)。
基于上述分析,可得到从阻抗角度解释的关于串补降低LCC-HVDC 系统稳定性的机理:LCC 交流阻抗在低频段(abc 坐标系)呈弱阻强感性,而线路串联电容的投入使得交流系统阻抗的低频特性由强阻弱感性变为弱阻强容性,这为受端交流系统与直流输电系统形成发散串联谐振创造了条件。
3.3 多台STATCOM 并联失稳机理
1)从定关断角控制特性的角度分析
附录B 图B4 展示了受端并联不同台数STATCOM 时,Gα2γ(s)的频率响应曲线。从图B4中可以看到,随着STATCOM 并联台数的增加,|Gα2γ(jω)|在中频处的值逐渐减小,意味着由串补电容导致的中频正反馈作用逐渐衰减。对于混合系统在高频段定关断角控制特性而言,当受端只并联1 台 或2 台STATCOM 时,|Gα2γ(jω)|在 高 频 处 的 值小于0 dB,这意味着触发角指令高频扰动在传递到关断角的过程中是衰减的,不容易对关断角形成发散型正反馈,系统依然能保持稳定。然而,当STATCOM 并 联 台 数 增 加 到3 台 时,|Gα2γ(jω)|在高频处出现尖峰,在相位过零点处对应的幅值约为16 dB,这意味着定关断角控制存在严重的“反调”效应,触发角指令高频扰动在传递到关断角的过程中是显著同相放大的,关断角容易形成发散型正反馈,系统失稳风险高。
基于上述分析,从LCC 的角度看,多台STATCOM 的投运导致系统失稳的机理可表述为:STATCOM 并联数目的增加改变了受端交流系统对触发角指令的响应特性,这驱使关断角在高频处形成发散型正反馈,从而降低了混合系统的稳定性。
2)从STATCOM 电导特性的角度分析
文献[19-20]指出:“如果变换器在任意频率处的输入电导非负,那么该变换器就不会产生不稳定性问题”。可以认为,如果变换器在系统特征频率处表现为负电导特性,那么该变换器就会增加系统在特征频率处产生发散振荡的风险。本节将简要分析STATCOM 输入导纳的主要特性。对比附录B 图B5 中的主导极点轨迹可以看出,STATCOM 锁相环[10]和直流电压外环对系统稳定性的影响相对较小,因此下面主要考察交流电压外环所形成的STATCOM 输入导纳特性。此外,由于交流电流环的响应速度远快于交流电压环,可以认为交流电压外环输出的电流指令即为STATCOM 的输出电流。
如果以流入STATCOM 的方向作为电流正方向,那么STATCOM 在dq坐标系下的输出电流ist,d、ist,q与输 入电压vi,d的关系式 可表示为:

式中:Vi0为逆变侧相电压幅值稳态值;kpv和kiv分别为交流电压环PI 控制器比例系数和积分系数。
根据式(7)并类比无源电路元件的s域表达式,交流电压环的作用可由负电导和负感纳的并联电路来表示,如附录B 图B6 所示。从图B6 可知,交流电压环的控制特性天然使得STATCOM 的q-d耦合导纳Yst,qd(s)呈负电导特性。dq导纳的物理意义不易于理解,因此根据导纳在不同坐标系下的转换关系,可将其转换为abc 坐标系下的导纳YSTp(s)。附录B 图B7 给出了STATCOM 正序输入电导GSTp在0~200 Hz 区间的频率特性。GSTp的简要推导过程如附录B 图B8 所示,此处不再赘述。
从附录B 图B7 中可以看出,GSTp在50~200 Hz范围内小于0,呈负电导性,并且其值随着并联台数的增加而减小。这表明STATCOM 并联数的增加会减弱系统在50~200 Hz 范围内的阻尼。而dq坐标系下的频率区间110~140 Hz 与abc 坐标系下160~190 Hz 的正序频率对应,落在STATCOM 电导为负的区间内。因此,从STATCOM 导纳特性的角度看,STATCOM 运行台数增加导致系统失稳的机理可表述为:交流电压环使其输入导纳在高频段内呈负电导性,且该负电导随着其投运数的增加而变小,削弱了混合系统在高频处的阻尼。
4 改善系统小信号稳定性的附加控制方法
为了改善混合系统的中高频动态特性,本章从控制系统改进的角度提出了如图5 中红色部分所示的附加控制。所提附加控制包括两部分:附加于LCC 控制系统内的触发角指令反馈控制(firing angle order feedback control,αFBC)以 及 附 加 于STATCOM 控制系统内的有功电流补偿控制(active current compensation control,ACCC)。图5中:γref和βi分别为LCC 逆变侧关断角指令和触发角指 令;udc,ref和分别为STATCOM 直流侧电压指令值和直流电压环PI 控制器;其余变量含义详见下文。
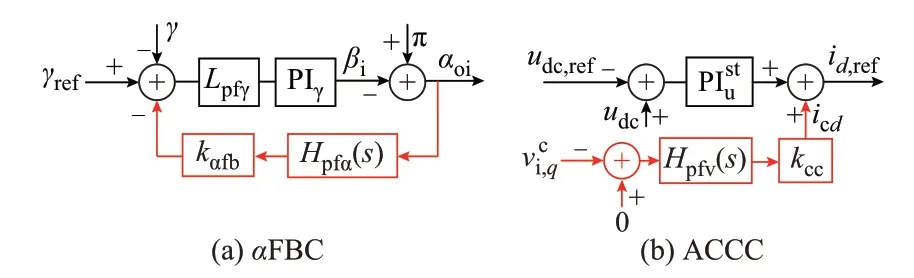
图5 所提方法的控制框图Fig.5 Control block diagram of proposed method
4.1 αFBC 部分
4.1.1αFBC 结构及其对主导极点的影响
经仿真研究,本文发现kαoγ对系统中频主导极点p5,6具有重要影响。kαoγ的原始值为-sinαi0/sinγ0=-2.38。从 该 关 系 式 可 知,kαoγ主 要 决 定 于αi0及γ0。然而,通过改变αi0或γ0的方式修改kαoγ则可能改变系统的稳定运行状态。因此,为了达到改变Δαoi对Δγ的作用强度这一目的,本文提出了附加于LCC 逆变侧控制系统的αFBC。
αFBC 由一阶高通滤波器Hpfα(s)和反馈增益kαfb组成,其中Hpfα的作用是滤除触发角指令的直流分量而通过谐振频率分量。由此可知,αFBC 在不影响逆变器触发角和关断角稳态值的情况下,能实现与修改kαoγ一样的效果。为了实现改善系统中频稳定性的目的,Hpfα截止频率应小于48 Hz(p5,6),因此本文选取其截止频率为10 Hz。图6(a)给出了当kαfb分 别 取 0、-0.5 和-1.1 时 含 串 补 及 3 台STATCOM 时的主导极点轨迹。从图6(a)中3 条轨迹的相对位置可以看出,kαfb取值越小,p5,6越向左半平面内移动,这表明αFBC 能改善混合系统的中频稳定性。

图6 所提控制方法对混合系统稳定性的影响(投入3 台STATCOM)Fig.6 Impacts of proposed control method on stability of hybrid system (with three STATCOMs)
4.1.2αFBC 的物理含义
从3.2 节 可 知,kαoγ体 现 了Δαoi对Δγ的 直 接 影响,改变其大小可直接调节定关断角控制的“正调”程度,进而改变系统的稳定裕度。图4 中绿色和黄色 曲 线 画 出 了kαoγ分 别 取-2.5 和-3.5 时 定 关 断 角控制的频域响应特性。从图4 中黄色曲线可以看出,如 果 将kαoγ从-2.5 减 小 到-3.5,中 频 段 的|Gα2γ(jω)|进一步从5 dB 衰减到-5 dB,发散正反馈效应被削弱,系统中频稳定性得到增强。该对比结果表明,减小kαoγ能抑制关断角在中频段形成发散正反馈,从而改善系统中频稳定性,这是kαoγ的基本物理意义,也是提出αFBC 的理论依据。因此,αFBC的物理含义是增加一条Δαoi对Δγ的直接作用支路,进而等效实现对kαoγ的修改。
4.2 ACCC 部分
4.2.1 ACCC 结构及其对主导极点的影响
ACCC 将0 与 锁 相 环 输 出q轴 电 压作 差 后 通过一阶高通滤波器Hpfv(s)和比例控制器得到有功电流补偿值icd,然后icd与直流电压控制器输出的电流指令相加得到最后的d轴电流指令值id,ref。在ACCC 中,kcc为补 偿增益,而Hpf(vs)则用 于滤除的直流分量且其截止频率设为20 Hz(须低于p3,4频率120 Hz)。
当kcc分别取0、2 和5 时,混合系统的主导轨迹变化规律如图6(a)至(c)所示。当kcc=0 时,高频主导 极 点p3,4向 右 半 平 面 远 离 虚 轴,如 图6(a)所 示。当kcc=2 时,p3,4轨迹虽然仍在右半面内,但已经紧挨虚轴,即系统高频阻尼得到增强,如图6(b)所示。当kcc增大至5 时,p3,4轨迹的大部分已移动至左半平面内,系统高频稳定性大为改善,如图6(c)所示。上述轨迹变化规律表明,所提ACCC 能提高多台STATCOM 并联运行时混合系统的稳定性。
4.2.2 ACCC 的物理含义
以流入STATCOM 的方向作为电流正方向,那么ist,d与vi,q的关系式为:

式中:Thv为Hpfv(s)滤波时间常数。
根据式(8),ACCC 可用电导与容纳的串联电路等效表示,如附录C 图C1(a)所示。图C1(a)中电导gcc=1 000kcc/(kstVi0),容 纳bcc=[1 000kcc/(kstVi0)]Thvs。由图C1(a)可见,ACCC 相当于给STATCOM 添加 了 一 条 阻 容 性 的d-q耦 合 导 纳 支 路Yst,dq(s)。图C1(b)画出了加入ACCC 前后STATCOM 在abc坐标系下的正序电导GSTp的频率特性曲线。从图C1(b)可见,加入ACCC 后GSTp变大,STATCOM在60~200 Hz 范围内的负电导性得到改善,表明ACCC 的应用能增加STATCOM 在该频域内(与dq域的10~150 Hz 对应)的阻尼,从而能提高多台STATCOM 并联运行的稳定性。
通过上述分析,可从频域导纳的角度给出ACCC 的物理意义:ACCC 相当于在STATCOM 的d-q耦合路径上增加了一条呈正电导性的阻容串联支路,而该支路能增加STATCOM 的正电导性,进而改善STATCOM 的阻尼特性。
4.3 所提控制方法在不同短路比条件下的适用性
为了探究αFBC 和ACCC 在其他工况下的适用性,本文画出了受端交流系统短路比分别取2.0 和3.0 时,混合系统在应用所提控制方法前后的主导极点轨迹对比图,如附录C 图C2 所示。从图C2 中无附加控制下的轨迹可以看出,当受端交流系统短路比取不同值时,p5,6对应的频率变化不大,依然在48 Hz 附近。串补电容阻抗与频率成反比,主要影响交流系统阻抗在低频段的频率特性(abc 坐标系下的低频)。因此,工程中报告的由电容引起的在abc 坐标系下的谐振频率一般在10 Hz 以内[5,11]。而abc 坐标系下10 Hz 以内的振荡频率对应于dq坐标系下40~50 Hz 的振荡频率。这是短路比大小对中频主导极点频率影响不大的原因。此外,图C2 中无附加控制下的轨迹显示,即使短路比变化,p3,4对应的频率在110~140 Hz 之间,远高于ACCC 中高频滤波器的截止频率20 Hz。如上所述,在不同短路比工况下,系统中高频谐振频率均变化不大,因此所提控制方法依然奏效,如图C2 中所提控制方法下的曲线所示。
图5 所示附加控制在1 台和2 台STATCOM 场景下的理论结果见附录C 图C3 和图C4,本节不再赘述。
5 仿真验证
本章将利用在PSCAD/EMTDC 中搭建的图1所示的混合系统电磁暂态模型来验证第2 章中的理论分析的正确性和第4 章中附加控制方法的有效性。
5.1 串补及STATCOM 的影响验证
当电磁暂态仿真模型运行至2.0 s 时在交流线路中投入串补度Kc=0.37 的串补电容,随后LCC 关断角γ的响应波形如图7(a)所示。在受端换流站不投入STATCOM 的工况下,关断角在投入串补后逐渐发散振荡,振荡频率约为46 Hz,如图7(a)中蓝色曲线所示。该仿真结果表明投入串补会引发系统中频振荡,从而验证了2.2 节的分析:串补会降低系统的中频稳定性。

图7 投入串补或第3 台STATCOM 时关断角的响应波形Fig.7 Response waveforms of extinction angle after applying series compensation or the third STATCOM
然而,当逆变站有1 台STATCOM 运行时,关断角在投入串补后依然能维持稳定,如图7(a)中红色曲线所示。通过对比红色和蓝色曲线可知,投运单台STATCOM 能削弱投入串补带来的负面影响,有利于混合系统中频稳定性,与2.2 节的理论分析结果一致。图7(b)给出了混合系统在2.0 s 投入第3 台STATCOM 后的响应波形。在此工况下,关断角在2.0 s 后以124 Hz 的频率振荡,如图7(b)中红色曲线所示。此仿真结果表明,当STATCOM并联运行数量增加时,混合系统的高频稳定性会变差,验证了2.3 节理论分析的正确性。
5.2 附加控制方法的效果验证
本节设置了增加kpγ和投入第3 台STATCOM这2 种运行条件恶化的情况以验证附加控制方法(kαfb=-1.1,kcc=5)的有效性,所得仿真结果如图8所示。从图8(a)中蓝色曲线可以看出,当kpγ在2.0 s时从0.35 增加到0.80 后(意味着系统阻尼变弱),未应用附加控制措施的混合系统(含串补及1 台STATCOM)出现了46 Hz 左右的中频振荡现象。但是,当混合系统投入附加控制措施后,同样的情况下系统仍能保持稳定,如图8(a)中红色曲线所示。这一仿真对比结果表明,附加控制方法能改善混合系统的中频稳定性,验证了4.1 节的分析结果。
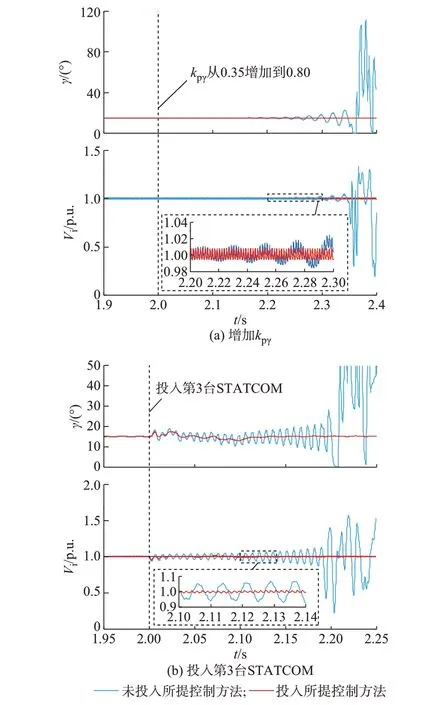
图8 在恶化系统运行参数的条件下应用所提方法前后关断角和交流电压幅值的响应波形对比Fig.8 Response waveform comparisons of extinction angle and AC voltage amplitude before and after applying proposed method under condition of deteriorating system operation parameters
图8(b)所示仿真波形对比了投入附加控制措施前后多台STATCOM 并联运行的动态特性。5.1节的仿真结果已经证明,未投入所提控制方法时,混合系统在投入第3 台STATCOM 后产生了128 Hz高频振荡,如图8(b)中蓝色波形所示。4.2 节的分析结果表明,附加控制方法能增强混合系统的高频阻尼。因此,当投入附加控制方法后,即使在2.0 s时投入第3 台STATCOM,混合系统仍能保持稳定,如图8(b)中红色波形所示,从而验证了该方法对多台STATCOM 并联运行动态特性的改善效果。
为了验证附录C 图C2 所示理论结果的正确性,附录C 图C5(a)和(b)分别给出了短路比为2.0 和3.0 时的电磁暂态仿真结果。对比图中无附加控制和含所提控制方法下的曲线可知,在不同短路比工况下,应用所提控制方法后,由串补电容引起的中频振荡和由多台STATCOM 并联引起的高频振荡均能得到有效抑制。这些仿真对比结果进一步验证了所提控制方法在不同短路比工况下的有效性。
6 与定电压控制方式的比较
前文分析了逆变侧采用定关断角控制情形下混合系统的小信号稳定性。然而,定电压控制也是LCC-HVDC 逆变站常用的控制模式[21]。比较这2 种控制方式下混合系统稳定性差异对实际工程的运行有一定的指导意义。为此,本章首先给出LCC 逆变站为定电压控制时串补和STATCOM 对混合系统稳定性影响的分析结果,然后简要讨论这2 种控制模式对系统稳定性影响不同的原因。
6.1 逆变站为定电压控制情形下的稳定性分析结果
6.1.1 小信号模型
当逆变站采用定电压控制时,LCC-HVDC 的小信号模型如附录D 图D1 所示。图D1 中,Kiu(s)=sLdi-udi0/idi0,其余系数表达式和参数见附录A 式(A1)—式(A8)。图D2 给出了阶跃响应对比结果。该仿真中,定电压控制PI 控制器的比例系数kpu和积分 系 数kiu分 别 为0.5 和100。 在 受 端 不 含STATCOM 和并联2 台STATCOM 这2 种工况下,小信号模型的直流电流和直流电压响应与电磁暂态模型对应的响应基本吻合,如图D2 所示,这验证了该模型的正确性。
6.1.2 理论分析结果
采用定电压控制情形下,串补及STATCOM对系统主导极点的影响如附录D 图D3 所示。从图D3(a)中无附加装置下的曲线可知,当不投入任何无功补偿装置时,LCC 的小信号稳定性主要由中高频主导极点p1,2决定(对应频率约为70 Hz),其相应的kpu临界值为1.8。投入串补后,混合系统增加了一对中频主导极点p5,6,其对应频率在40 Hz 左右,如图D3(a)中只投入串补时的轨迹所示。此时,kpu的临界值为1.6(p1,2)。图D3(a)中同时投入串补和1 台STATCOM 时的轨迹显示,再投入1 台STATCOM 虽然能使中频主导极点p5,6稍往左移,但混合系统kpu的临界值依然由p1,2决定,为1.6 左右。从上述结果可知,对于定电压控制的情形,混合系统虽然在投入串补后增加了一对40 Hz 左右的中频主导极点,但其kpu临界值在投入前后的差异较小,约为0.2。因此,串补对混合系统整体的稳定性影响不大。此外,对比只投入串补和同时投入串补和1 台STATCOM 时的轨迹可知,投入单台STATCOM 对系统稳定性的影响也较小。
附 录D 图D3(b)展 示 了 投 运1 至3 台STATCOM 时系统的主导极点轨迹。对比图D3(b)中3 条轨迹可知,在增加STATCOM 数目的过程中,p5,6位置变化不大,而p1,2有向左半平面移动的趋势。对于高频主导极点p3,4(130 Hz)而言,其随着STATCOM 投运数的增加大幅向右半平面移动。尤 其 当 投 运3 台STATCOM 时,p1,2完 全 处 于 右 半平面内,混合系统失稳。上述结果表明,并联台数的增加对系统中频和中高频稳定性的影响相对较小,但会显著恶化系统的高频稳定性。
6.1.3 仿真验证结果
为了验证上述理论分析的正确性,在PSCAD/EMTDC 软件中也搭建了逆变站为定电压控制情形下混合系统的电磁暂态仿真模型,所得仿真结果如附录D 图D4 所示。从图D4(a)可以看出,在受端交流线路的串补度从5%增加到37%后,混合系统依然能维持稳定。该仿真结果表明,串补对系统稳定性的影响较小,与6.1.2 节理论分析一致。图D4(b)中不含ACCC 时的曲线显示,混合系统在并联2 台STATCOM 时能稳定运行,而在投入第3 台STATCOM 时却失去稳定,且振荡频率约为130 Hz。这一仿真结果表明,增加STATCOM 运行台数会降低系统高频稳定性,验证了6.1.2 节的理论分析。当STATCOM 加入ACCC 后,混合系统高频振荡被抑制,如图D4(b)中含ACCC 时的曲线所示,表明ACCC 在LCC 为定电压控制的情形下同样有效。
6.2 逆变站采用不同控制模式时系统稳定性存在差异的原因
对比6.1 节和前文的分析结果可知,与采用定关断角控制的情形相比,当逆变侧为定电压控制模式时,投入线路串补对受端交直流系统的小信号稳定性影响较小。目前,鲜见文献对这一现象进行解释。为此,本节将通过比较定关断角/定电压控制特性的差异,以及这2 种控制模式下LCC 阻抗特性的差异来解释上述现象。
1)定关断角/定电压控制特性的比较
与Gα2γ(s)的定义类似,同样可以定义用于描述LCC 定电压控制特性的控制灵敏度传递函数:
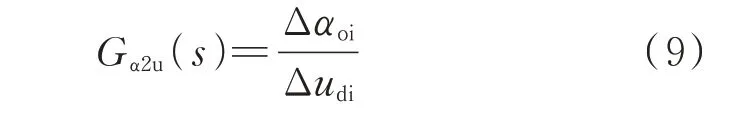
在逆变侧,较大的udi对应于较大的αoi。因此,对于定电压控制而言,其“正调”方向为:增大Δαoi使Δudi增加,与定关断角控制的“正调”方向相反。于是,如果Gα2u(s)在某一频率处穿过±180°,则表示Δαoi与Δudi在该频率处反相,定电压控制为“反调”,系统形成关于Δudi的正反馈,且如果|Gα2u(jω)|在该频率处很大,则有形成发散正反馈的风险。
附录D 图D5 画出了投入串补前后Gα2u(s)的频率响应曲线。从图D5 中含串补时的曲线可见,∠Gα2u(jω)在中频段穿越±180°线,表明投入串补后LCC 定电压控制特性在中频段形成了“反调”,混合系统对Δudi形成正反馈,这与定关断角控制的情形相同。不同的是,|Gα2u(jω)|在中频段从-3 dB 衰减到-12 dB,意味着该频段的扰动从Δαoi传递到Δudi的过程中被衰减,降低了Δudi形成发散正反馈的风险。图D5 中∠Gα2u(jω)穿越±180°线的频率与图D4 中p5,6的频率存在一定偏差,其原因是Gα2u(s)未包含Gdcr(s)和定电压PI 控制器。
综上,采用定电压控制时串补影响较小的原因是:定电压控制的“正调”方向与定关断角控制的相反,投入串补难以使逆变侧直流电压形成发散的正反馈。
2)阻抗特性的比较
当逆变站分别采用定关断角控制和定电压控制时,直流输电系统交流输入阻抗扫描值如附录D 图D6 所示。投入串补后受端交流系统阻抗在低频段(abc 坐标系,对应于dq坐标系的中频)呈弱阻强容性。因此,如果LCC 交流阻抗阻性越弱,感性越强,则交直流系统间越容易形成发散的低频串联谐振。而从图D6 可知,定关断角控制情形下LCC 的阻抗ZLCCγ与定电压情形下的阻抗ZLCCu在低频段的幅值接近,但ZLCCγ的相位要明显大于ZLCCu的相位,其中前者在60°左右而后者在30°上下。这一阻抗测量值的对比结果说明,当逆变站为定电压控制时,LCC的交流阻抗阻性更强、感性更弱,混合系统较难发生低频发散谐振。
7 结语
本文建立了受端含串补及多台STATCOM 的LCC-HVDC 系统的小信号模型,并基于系统主导极点轨迹研究了混合系统的小信号稳定性及其改善方法,所得主要结论如下:
1)串补能改善系统低频和高频的稳定性,但不利于系统中频稳定性。但整体而言,串补会降低系统的稳定裕度,这是因为串补会使关断角在中频处(dq坐标系)形成发散型正反馈;或者说串补使交流系统低频阻抗呈弱阻强容性,为LCC 与交流系统形成低频(abc 坐标系)串联谐振创造了条件。
2)STATCOM 能改善系统的中频稳定性,但随着其并联数量的增加,系统的高频稳定性(dq坐标系)会变差,其原因是增加STATCOM 台数会增加定关断角控制在高频处形成发散正反馈的风险;或者说STATCOM 在高频处呈负电导性,其并联数的增加会降低系统的高频阻尼。
3)αFBC 增加了一条触发角指令到关断角的直接作用支路,能抑制在中频处形成的发散型正反馈;而ACCC 等效于在STATCOMdq轴之间增加一条阻容串联支路,能改善STATCOM 的高频阻尼。所提控制方法的有效性通过了电磁暂态仿真的验证。
4)当逆变站采用定电压控制时,串补对系统稳定性的影响较小,这是因为定电压控制“正调”方向与定关断角控制相反,更不容易形成发散型正反馈;或者说采用定电压控制时LCC 的低频输入阻抗的阻性更强、感性更弱,更难引发串联谐振。
本文通过对比主导极点轨迹的变化揭示了混合系统中串补和多台STATCOM 运行的影响,并给端口变量赋予一定的物理含义后,从端口外特性层面解释了上述影响的机理,但端口内部关键变量之间的相互作用过程及作用特性尚未得到充分揭示,这也是后续需要进一步研究的内容。
本文研究过程中受到长沙市科技计划项目(kq2107005)的资助,谨此致谢!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

