考虑任务耦合的配电网边缘计算终端部署与任务分配方法
陈元榉,蔡泽祥,岑伯维,胡凯强,武志刚,康逸群
(华南理工大学电力学院,广东省广州市510641)
0 引言
随着电力物联网的发展,电力末端设备如传感器、智能电表等呈现海量接入的态势[1-2],异构多源的信息数据在爆发式增长的同时也催生出多元化、生态化的配电网业务需求[3-4]。配电网中的数据测点分散且分布广泛,传统主站的集中式处理难以提供可靠的数据处理支持,“一测点一机”的智能终端配置方式难以实现。边缘计算为实现信息就地化处理、计算资源供需平衡提供了重要技术手段。边缘计算终端(edge computing terminal,ECT)是边缘区域的信息、业务聚合中心,实现对若干分散测点的数据进行汇集、处理,使配电网数据处理呈现出“分布聚合”的特点[5-7]。
ECT 多采用分布式部署,多ECT 协同被广泛应用于处理边缘区域的自主决策业务[8-9]。业务的处理需要获取全域节点的数据信息,且在将业务分解为若干子任务进行处理时,各子任务需遵循一定的逻辑耦合关系[10-11]。在多ECT 协同系统中,每台ECT 管控一个节点簇(node cluster,NC),不同ECT部署与任务分配策略将导致计算资源的供需关系和服务质量产生偏差[12-15]。因此,合理决策ECT 的部署位置及其承担的任务,适应ECT 分布式部署与任务耦合下的计算资源供需平衡,对优化信息流分布、降低任务处理成本、提高资源利用率等具有重要意义。
目前,智能终端部署与多处理器系统中的任务分配是重要的研究课题,文献[16-17]提出了在分布式多代理系统中的任务分配方法与调度方法。时延、能耗或成本等是重要的评价指标,文献[18]提出了一种移动边缘计算技术下的智能设备部署与任务分配方法,可以使能耗最小化。文献[19]提出了利用微云部署降低任务卸载终端的概率,减少云服务器的延时、传输功耗。文献[20]提出了一种考虑业务可靠性的任务分配方法,实现任务卸载时的成本最小化。上述研究主要以达到能耗等某方面性能最优为目标,缺少考虑计算资源层面或通信层面的耦合关系以及多智能终端间的协同效应。文献[21]提出了一种基于需求分析的计算资源部署方法,为解决计算资源供需平衡提供了借鉴意义。
本文提出一种考虑配电网任务耦合的ECT 部署与任务分配方法。首先,提出基于NC 划分的边缘计算架构并提出任务处理模型,刻画任务的处理特征及不同任务间耦合关系。其次,建立考虑ECT部署与任务分配的双层模型,其中,上层模型求解任务在ECT 间的分配问题,下层模型求解ECT 在NC内的部署。再次,分析双层模型间的耦合关系,提出改进的K-means 法实现NC 的划分,并利用带边界条件的隐枚举法求解该双层模型。最后,利用算例验证了本文所提方法的有效性与可行性。
1 边缘计算架构与任务处理模型
1.1 基于NC 划分的边缘计算架构
根据配电网中节点的计算资源差异将系统节点分为数据节点(data point,DP)与边缘计算节点[22-23]。DP 分布广泛,其位置与配电网实际运行控制、接入对象相关,如开闭所、负荷开关、充电桩等在内的数据获取,DP 将待处理数据上传至最近的ECT。边缘计算节点部署有ECT,受限于计算资源与通信资源数量,ECT 仅管控一定范围内的DP,将ECT 管控的若干DP 构成的集合称为NC。ECT 是边缘区域的信息聚合中心,实现NC 内分散分布的DP 请求的任务聚合处理,即DP 的广泛分布与ECT管控的NC 共同构成配电网“分布聚合”的数据处理特征。边缘计算架构如图1 所示。
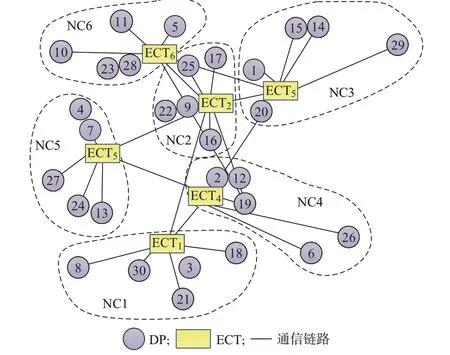
图1 配电网边缘计算架构Fig.1 Architecture of edge computing in distribution network
根据配电网业务处理时的数据来源差异将任务抽象为单节点请求和多节点请求任务两大类,即下文所述的单终端任务(single-terminal task,STT)和跨终端任务(cross-terminal task,CTT)。在CTT 的处理过程中,ECT 需要获取不同NC 内的处理数据,处理数据与任务间的耦合关系是边缘计算架构中多ECT 协同机制的基础。在多ECT 协同过程中,数据 交 互 方 式 包 括:1)NC 内 的DP 与ECT 的 数 据 交互,通信双方属于不同节点层级,构成边缘计算架构中的垂直式架构;2)不同ECT 间的数据交互,通信双方均为边缘计算节点,构成边缘计算架构中的水平式架构[24]。
1.2 任务的特征模型
1.2.1 STT 和CTT
STT 是指由单DP 请求的处理任务,在ECT 管控 的NC 内,各DP 的STT 请 求 由 该ECT 处 理。CTT 是指该类任务的处理需获取边缘区域中的多个NC 内DP 的采集数据,在ECT 间产生数据交互。一般而言,STT 的计算负荷与延时容忍度较小、任务周期较短;CTT 的计算负荷与延时容忍度较大、任务周期较长。
1.2.2 任务计算负荷
在通过建立任务的特征模型表征不同类型任务处理时,需要满足计算资源及延时容忍度,其中,对计算资源的需求表征为任务的计算负荷。计算负荷的大小与任务类型、处理数据量大小有关,表达式为:
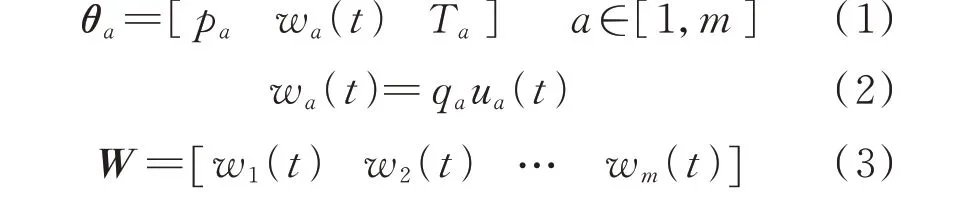
式 中:θa为 任 务a的 特 征 模 型;pa为 任 务a的 类 型;wa(t)为任务a在时刻t的计算负荷;Ta为任务a的延时约束;qa为处理pa类任务时单位数据量的计算负荷;ua(t)为任务a在时刻t的数据量;W为m个任务构成的向量。
1.3 任务处理耦合模型
1.3.1 任务处理时序逻辑链
将m个 任 务 分 为m1个STT 与m2个CTT,则m1+m2=m。将ECT 在满足STT 的处理需求后剩余的资源称为剩余资源,剩余资源的数量影响ECT 处理CTT 时的计算延时。在处理m2个CTT时,利用处理时序逻辑链表征跨终端业务分解的若干CTT 的耦合关系,CTT 的耦合关系表现为任务间的承接与并列关系。
配电网自动化与系统用户行为的相互作用使配电网的能量传输关系发生变化,ECT 承担的任务主要涉及用户侧的能量分析控制等计算,故将其统称为能量管理业务。将能量管理业务进行如下分解:CTT1表示电压与无功控制;CTT2表示电力负荷管理;CTT3表示设备管理;CTT4表示停电与检修管理;CTT5表示源荷储微交易;CTT6表示配电运行辅助决策。图2 为能量管理业务分解为6 个CTT 时的处理时序逻辑关系[8-9,25-27]。在同一处理周期中,CTT 的承接关系表现为任务在时间轴上的先后顺序,同一时序逻辑链上位于前方的CTT 处理完成后,将处理结果传输至下一CTT 并触发其执行,如图2 中的CTT1与CTT3所示。
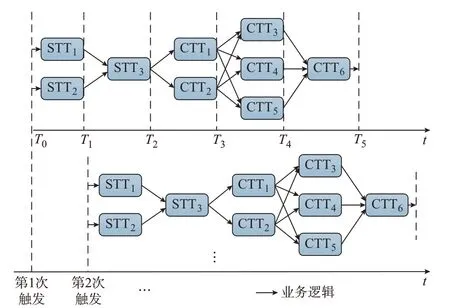
图2 多周期耦合下能量管理业务的处理时序逻辑链Fig.2 Time sequential logic chain of energy management business processing under multi-cycle coupling
CTT 的并列关系是指若干任务在被触发后可同时进行处理。并列任务组成的整体与其他CTT构成承接关系,例如CTT3、CTT4、CTT5构成并列关系并组成整体,与CTT2、CTT6构成承接关系,利用变量yav刻画时序逻辑链中各CTT 的数据传输方向,表达式为:

1.3.2 多周期耦合的跨终端业务计算负荷
在稳态运行时,任务处理呈周期性,图2 中能量管理业务的一次触发的周期为T0至T5,其中,T0为任务的开始时刻,T5为任务的结束时刻。由于CTT处理时的承接关系,在时刻t下,同一处理时序逻辑链中存在单个承接任务或多个并列任务处于处理状态的情况。当业务请求达到稳态时,时刻t下会存在多个任务周期,如图2 中的多周期耦合下的处理时序逻辑链。每台ECT 为任务分配独立的资源空间,同一ECT 内的不同任务相互独立。不同周期下的处理任务同时进行,使每台ECT 最多可同时运行5 个处理周期中的同一个CTT。在如图2 所示的CTT 的稳态处理过程中,时刻t下能量管理业务产生的计算负荷l(t)表达式为:
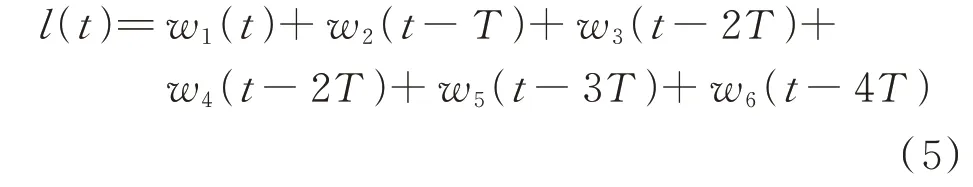
式中:T为业务触发的时间周期。
为满足电力物联网中海量设备与用户的数据处理需求,单台ECT 受限于计算容量和获取数据数量,仅能处理所在区域内的部分计算任务。而利用多ECT 的协同,可灵活调用各ECT 计算资源,处理较大范围内的计算任务。若能量管理业务中各子任务多周期并发处理,会使数据处理性能变差,在传输与计算过程中产生更多的处理延时。若按照一定的任务处理先后顺序,根据不同处理周期内CTT 计算负荷的差异调用系统可用的ECT 资源,可使资源利用更加合理,并获得更优的处理性能。
2 ECT 部署与任务分配优化模型
在上述的边缘计算架构中,ECT 数量有限,其分布应考虑使DP 可都处于ECT 的服务范围内。由于DP 处理数据、任务计算负荷的波动性与差异性,以及ECT 部署与任务分配策略的不同,导致计算资源供需关系、任务处理服务质量产生偏差。为解决ECT 分布式部署与任务耦合的计算资源供需平衡的适应性问题,本文提出ECT 部署与任务分配优化的双层模型,其中,上层模型求解任务在ECT 间的最优分配,下层模型求解ECT 在NC 内的最优部署。
2.1 上层模型
在上层模型中,根据已知的ECT 部署结果,确定使总成本最小的任务分配方案,采用0-1 变量χae表 征 任 务a与ECTe间 对 应 关 系,e∈{1,2,…,K},其中K为系统ECT 的数量,表达式为:

1)目标函数
任务处理需要占用计算资源和通信资源,并产生能耗。由于任务的计算负荷随处理的数据量发生变化,导致数据处理与传输过程中占用的计算资源与通信资源发生变化。此外,利用能耗成本表征不同ECT 被占用不同数量的资源时产生的能耗。上层模型的目标函数为:
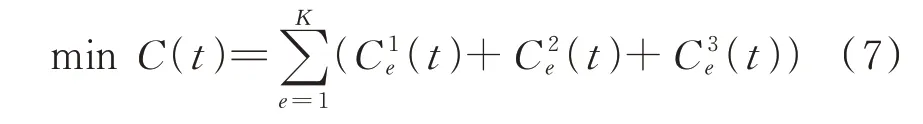
式中:C(t)为在时刻t系统任务处理的总成本;e为ECT 的编号;(t)、(t)、(t)分别为ECTe处理任务时产生的计算、能耗和通信成本。
2)计算成本
在ECT 中,不同任务被放置于不同处理容器中,并根据任务属性为每个容器分配一定数量的计算、通信资源,使在满足STT 的延时约束条件下为CTT 提供更多的剩余资源。在实际应用中,由于计算负荷随数据的变化,计算成本的表达式为:
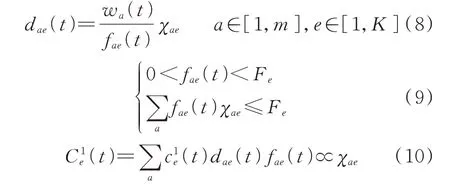
式中:dae(t)为ECTe处理任务a时所需的时间;fae(t)为ECTe分配给任务a所属容器的计算资源;(t)为占用ECTe的单位计算资源所需的成本;Fe为ECTe的计算资源总量;∝为正比符号。式(9)为ECTe分配任务a时应满足的计算资源约束条件。
3)能耗成本
电力系统中ECT 数量及其运行能耗巨大。在可持续发展与“双碳”目标下,减少处理设备产生的能耗至关重要。处理设备产生的能耗与其承担的处理任务有关,即任务的不同分配导致设备的不同能耗[26-28],ECT 协同过程中处理任务的合理分配,既有利于提高设备的资源利用率,又有利于减少能耗的产生。ECT 产生的能耗与当前运行的计算资源数量关系为:
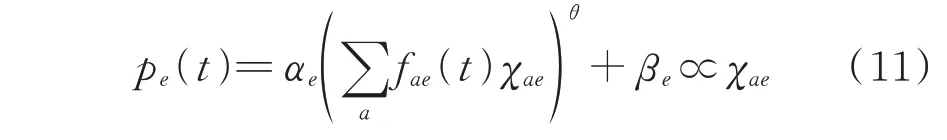
式中:pe(t)为ECTe的能耗功率;αe、βe、θ为 能耗参数,且αe,βe>0,θ∈[2.5,3.0]。
因此,能耗成本为:
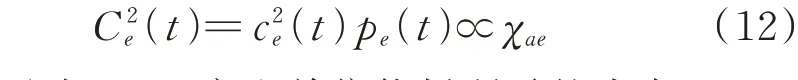
由式(6)至式(12)可得,上层模型目标函数的结果取决于通信成本及χae。当下层模型确定最优的通信方案时,通信成本随之确定,故上层模型目标函数的最小值等价于最优的任务分配结果,即变量χae的全体取值。在任务分配过程中,在满足约束条件下,任务间的分配相互独立,其不同的分配结果导致ECT 的数据处理性能、数据传输延时等产生差异。
2.2 下层模型
1)目标函数
ECT 是数据处理的主要设备,其部署会影响系统数据传输结构、特性。为优化数据流分布、减少通信资源的占用,建立下层模型的目标函数为:
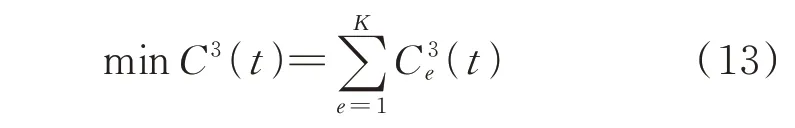
式中:C3(t)为总的通信成本。
2)通信延时
节点间的数据交互存在2 种方式:(1)垂直式架构下DP 与ECT 间的通信;(2)水平式架构下各ECT 间的数据交互。节点间的通信方式包括无线方式和有线方式。根据DP 所处位置采用的通信方式不同,例如:负荷开关采用低压载波通信,充电桩采用远距离无线电(long range radio,LoRa)通信等。利用0-1 变量χie与χee'表征节点间的通信关系,数据传输延时为:

式中:die为时刻t第i个DP 与ECTe间传输数据量为uie(t)时产生的传输延时,其中,i∈[1,n],n为系统DP 的数量;dee'(t)为时刻t在ECTe与ECTe'间传输数据量为uee'(t)时产生的传输延时;Rie,ee'(t)为时刻t利用香农公式计算得到的第i个DP 与ECTe(或ECTe与ECTe')间的信息传输速率;Bie,ee'为第i个DP与ECT(e或ECTe与ECTe)'间 的 带 宽;Nie,ee'(t)为 时刻t在第i个DP 与ECTe(或ECTe与ECTe')间的信噪比。
3)通信成本
参考国内外相关运营商的通信资费情况,采用流量方式对本文的通信成本进行刻画。通信流量以数据传输时占用的通信资源数量与使用时间的乘积进行表征,则通信成本表征为单位数据传输成本与传输数据量的乘积,表达式为:
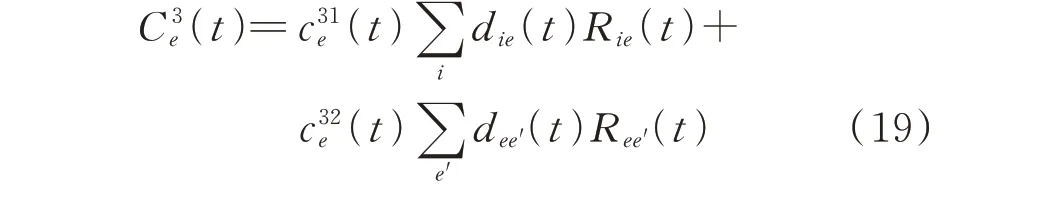
4)延时约束
配电物联网中的各任务都具有处理延时容忍度,任务的服务延时主要分为数据上行与指令下行的传输延时和ECT 处理数据时产生的计算延时。针对垂直式架构下的处理任务,其处理任务为STT,延时约束模型如式(20)所示。针对水平式架构下的服务延时,由于CTT 在处理时序逻辑链的位置不同,导致ECT 间的数据传输方向不同,CTT 类任务的处理延时约束模型如式(21)所示,而如图2所示的一个任务周期内的能量管理业务的延时约束如式(22)所示。为处理时序逻辑链上各承接部分的延时与各并列部分延时的最大值之和不超过能量管理业务的延时容忍度。
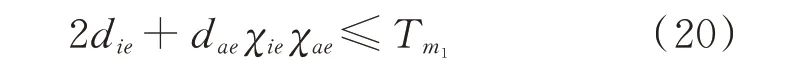
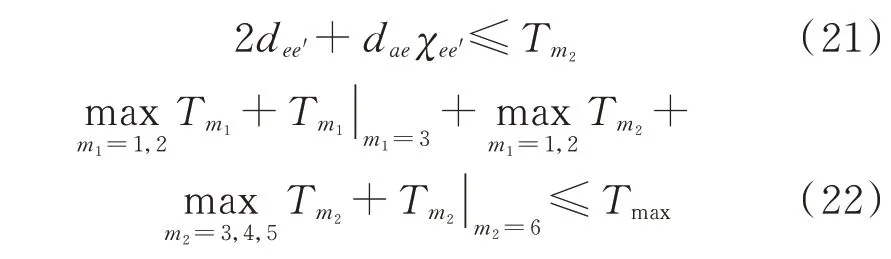
式中:Tmax为能量管理业务的延时容忍度。
2.3 上、下层模型间的耦合关系
上层模型以优化系统任务处理成本实现任务在ECT 间的分配,下层模型以优化系统的信息流分布实现ECT 的最优部署。由附录B 第B1 章的决策变量分析,得到如图3 所示的上、下层模型间的耦合关系,双层模型的耦合作用过程如附录B 第B2 章所述。
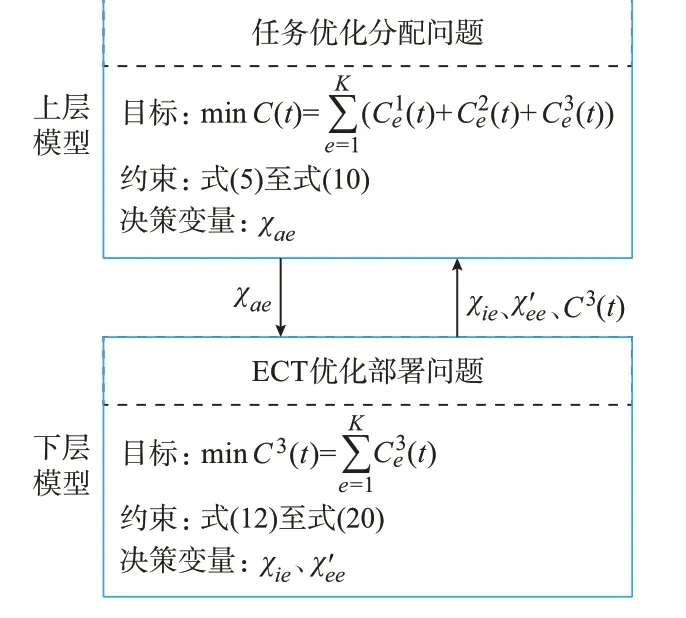
图3 上、下层模型间的耦合关系Fig.3 Coupling relationship between upper and lower models
3 模型求解
3.1 模型假设与简化
3.1.1 模型假设
假设1:为保证数据处理的可靠性,NC 内DP 数据量的变化可实时测得;DP 数据波动满足正态分布,且DP 之间相互独立;DP 间的相对位置可知。
假设2:各任务的单位数据量的计算负荷可知;能量管理业务的处理时序逻辑可知。
假设3:ECT 内部为容器分配计算资源的时间可忽略不计;容器的创建与销毁可实时完成。
3.1.2 模型简化
在上述ECT 的部署过程中,考虑n个DP 请求的STT 产生的计算负荷,以及不同ECT 部署与任务分配策略下对计算、通信资源的占用等,使对决策变量χie的求解等价为一个非确定性多项式(nondeterministic polynomial,NP)难问题,为双层模型的求解带来困难[29]。在实际ECT 部署中,考虑到DP的计算负荷变化存在波动区间,且NC 内的DP 数量差异易造成ECT 负载的不均衡,结合实际DP 的位置分布,提出在求解双层模型前先确定K个NC 的划分,ECT 的部署位置从每个NC 中选择。
3.2 NC 划分方法
边缘的数据源节点依赖于边缘计算终端的处理资源,故在采用K-means 法对节点进行划分时,考虑以边缘计算终端的数量K为NC 划分数量。每个NC 内的节点数量不同使ECT 的计算负荷、数据传输量产生较大差异,进而影响ECT 的负载率及每个节点可利用的资源数量,从而导致节点的数据处理产生较大差异。所以,在利用K-Means 法进行K个NC 划分时,以每个NC 内的节点数量均衡为划分标准。为使各ECT 在处理STT 时的负载均衡,将系统n个DP 均分为K个NC,则ECTe管控的DP 数量ne为:
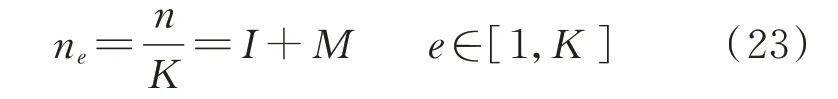
式中:I为ne计算结果的整数部分;M为ne计算结果的小数部分。当M≠0 时,系统存在K(1-M)台ECT 管控的节点数为I,KM台ECT 管控的节点数为I+1。
根据组合理论,上述NC 约共有n!/(Kne!)种,此外,还需要计算每个NC 内的各节点间的距离,计算量大。而对于K-means 法等节点聚类方法,在节点划分过程中并未考虑每个NC 内的DP 数量,会使ECT 的负载均衡度降低。为此,提出一种结合启发式与K-means 法的NC 划分方法,求解算法1 见附录A 表A1,实现流程见附录A 图A1。
3.3 双层模型求解算法
双层模型求解适用方法分析见附录B 第B3章[30-34]。不考虑垂直式架构下任务分配的影响时,易证每个NC 内存在唯一DP 使处理基本负荷时的通信延时最小。确定每个NC 内的上述DP,将其作为ECT 部署的初始节点,计算此时的总成本,并将其设为初始边界。双层模型的求解流程见附录A图A2,基于隐枚举法求解双层模型的算法见附录A表A2。本文采用隐枚举法,其求解本质与联立求解的枚举法相同,均是在所有可行解中寻找最优解,只是在求解过程中,本文利用不同可行解的特征(可行解与ECT 部署节点的分布、承担任务的数量相关),排除一些明显使目标函数远离最小值的可行解,即缩小每次的求解域。此外,在第4 章中,通过多次仿真实验,比较了隐枚举法与方程组联立求解的结果,两者具有一致性,可知该最优解为全局最优解。
4 算例分析
4.1 参数设置
为探究不同节点的数据变化情况下,能量管理业务分解的各个子任务在不同ECT 间的分配,本文以如图1 所示的某地区30 节点配电系统为例进行仿真 分 析[20],设 图1 中 节 点1 至5 为 开 闭 所、节 点6 至12 为 负 荷 开 关、节 点13 至16 为 充 电 桩、节 点17 至21 为分支线开关、节点22 至24 为分布式电源、节点25 至30 为用户分界开关。设系统配置6 个ECT,其参数见附录A 表A3[35],ECT 的单位计算、能耗及通信成本见表A4。DP 的STT 计算负荷变化曲线见图A3(a)。能量管理业务分解的6 个CTT 的时序逻辑链如图2 所示,各CTT 的计算负荷变化曲线见图A3(b),系统请求能量管理任务的时间间隔为2 s。STT 与CTT 的相关参数见表A5。
4.2 NC 划分
设DP 采集的数据量满足[0.16,0.24]MB 间的正态分布,以各个DP 数据的均值作为NC 划分时的权重。为得到较好的聚类结果,首先需选择合适的节点作为初始聚类中心。初始聚类中心的选取与DP 的分布相关,计算各DP 与其他DP 的相对距离之和,确定节点9 与其他DP 的加权相对距离之和最小,选取与节点9 的加权距离最大的DP(节点21)作为第1 个初始聚类中心,并将距离D21及距离其最近的4 个DP(节点3、30、18、8)划入同一NC 中。从剩余未被划分至NC 中的DP 中选取距离节点9 最远的DP(节点29)作为另一初始聚类中心,并重复上述步骤直至形成初始6 个NC。聚类中心的确定路径及最终的NC 划分结果见附录A 图A4。
4.3 ECT 部署与任务分配
NC 内每一个DP 均可作为ECT 的部署节点,且每台ECT 部署彼此独立,6 个CTT 可部署于任一台ECT 上,故上述双层模型的可行解个数为7.29×108。利用隐枚举法设置的初始边界中选取的ECT部署节点分别为:节点3、9、15、19、27、28。将上述DP 连接为闭合五边形,见附录A 图A4,不考虑五边形外的DP 作为ECT 的部署节点,此时排除可行解个数约为7.21×108。在上述ECT 部署方案下,计算各ECT 的剩余资源,在满足任务处理延时约束下,排除能耗成本过高的任务分配方案,如将多个子任务分配在同一台ECT 上,能耗成本的增加量大于通信成本的减小量,此时排除的可行解个数约为7.44×106,将ECT 部署单个CTT 设为边界2。迭代求解出使处理成本最小的ECT 部署与任务分配方案,结果见表A6。根据上述ECT 部署与任务分配结果,各CTT 的处理延时如图4 所示,各ECT 的计算资源利用率变化如图5 所示,各成本如表A7所示。
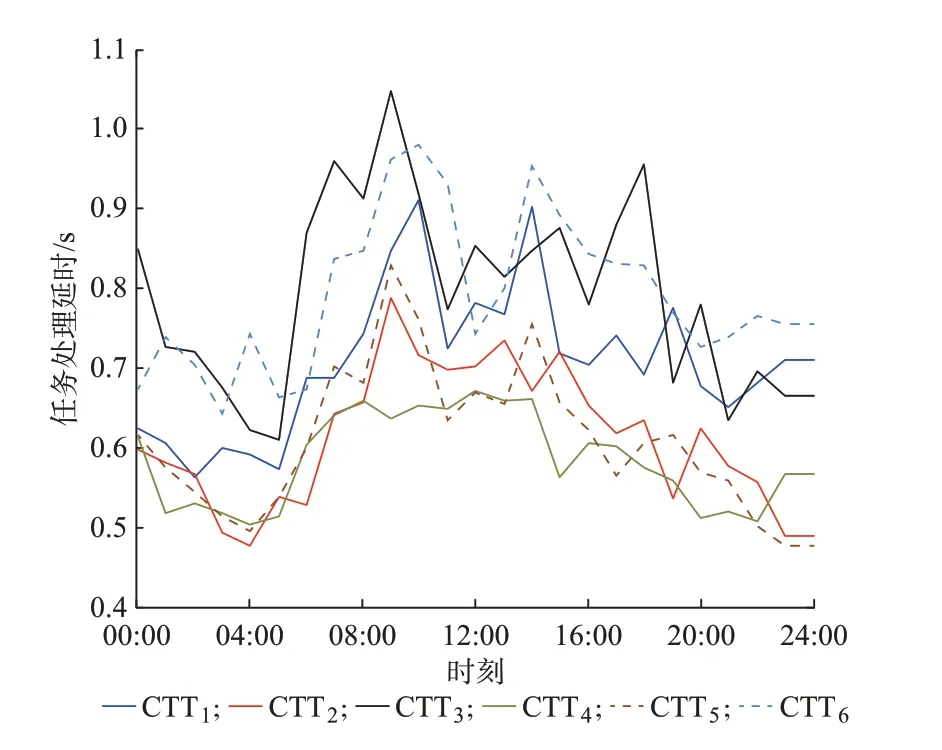
图4 各CTT 处理延时曲线Fig.4 Processing delay curves of each CTT
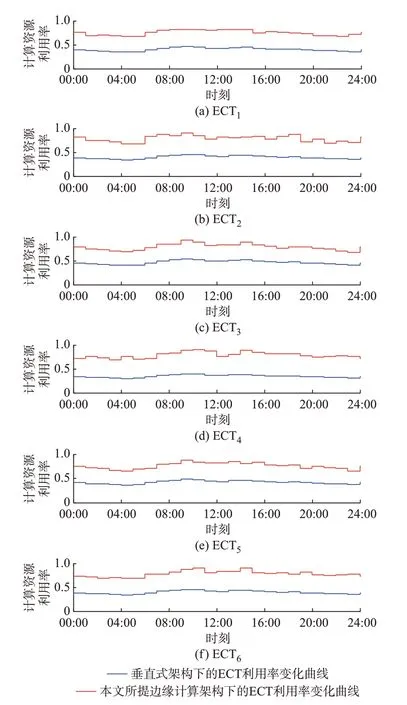
图5 ECT 的计算资源利用率曲线Fig.5 Computing resource utilization rate curves of ECT
在不同ECT 部署与任务分配策略下,任务计算负荷的变化会对计算资源供需关系及业务服务质量产生影响。附录A 图A5 为峰值负荷增加时各ECT的计算资源利用率变化情况。
4.4 结果分析
在NC 划分过程中,合理的初始聚类中心的选取可有效减少聚类所需的迭代计算次数。在选取第3 个初始NC 时,选择节点26 作为初始聚类中心,距离节点29 最近的4 个DP 中,节点18 已被划分至第1个初始NC 中,因此利用剩余DP 中距离最近的节点2 代替节点18。在利用初始聚类中心形成的6 个初始NC 中,有4 个NC 与最终的NC 划分结果一致,则其在第2、3 次计算后得到的密度中心相同。即利用上述方法最少可在3 次迭代计算后得到系统NC 划分的结果。在DP 处理数据发生±20%的变化时,ECT 处理NC 内DP 请求的STT 时负载的不均衡度小于9.4%。
上、下层模型可行解的个数分别为46 656 和15 625。若仅考虑垂直式架构下的任务处理,则ECT 部署于NC 的密度中心将使处理成本最小。水平式架构下,任务间的耦合关系使ECT 之间存在数据交互,即产生对通信资源的占用,导致ECT 的部署位置偏移NC 的密度中心,从而降低网络传输延时。ECT 部署时设置的第1 个迭代边界为上述的密度中心,使下层模型的可行解个数减少15 463 个;任务分配时,均匀分配可有效减少ECT 的能耗,排除将多个任务分配在同一ECT 上的可行解,进一步将可行解的个数减少为原始可行解个数的0.016%。双层模型优化结果与边界2 的任务分配与ECT 部署策略相比,总成本降低约16%,计算成本与通信成本分别降低约15.5%与26.6%。
典型的边缘计算架构为文献[26,36]提出的垂直式架构,其边缘计算方法(记为方法1)与本文所用的计算方法在处理配电网业务时,各ECT 的资源利用率变化曲线如图5 所示。由图5 可知,本文所提的边缘计算方法得到的资源利用率大于方法1 的资源利用率。相较于方法1,ECT 的资源利用率平均提高约30%,最大可提高约39%。在考虑系统配置10%的计算资源容量时,本文所提方法相较方法1而言,可短时承载的尖峰负荷提高约17%。区域边缘计算终端可承载的负荷增加,为后续数据源节点负荷的增加提供足够的消纳能力,由此产生的效益随之增加。此外,与随机ECT 部署与任务分配策略相比,相同资源配置与处理任务下,任务处理开销减少约35%,对计算资源的占用减少14%~16%。
5 结语
针对当前配电网物联网的ECT 部署与任务分配问题,本文提出利用任务的耦合关系实现在稳态运行时的处理成本最低。任务的计算负荷模型、处理架构是ECT 部署与任务分配的基础,计算负荷模型实现对ECT 计算资源利用率、任务计算复杂度进行定量表征。垂直式架构下ECT 与DP 交互,任务处理方式单一,而水平式架构下ECT 间相互协同,在两者结合作用下,任务分配更具灵活性,同时减少云主站计算压力,发挥多边缘计算终端的协同效应,降低任务处理开销。ECT 部署应关注稳态时各ECT 的计算资源利用率,合理化信息流分布,优化ECT 承担的任务类型。任务分配应关注ECT 的管控区域的计算负荷变化,确定各ECT 当前可调用的计算资源数量,合理化任务分配,合理划分ECT 的管控区域。
本文基于将计算负荷较大、跨终端处理的业务分解为若干子任务并将其分配至各台ECT 的方法,适用于其他不同处理逻辑的业务类型。同时,本文从计算负荷的角度研究ECT 计算资源利用率,为后续不同类型和不同处理时序逻辑的任务卸载、资源动态调度、信息流分布优化等打下基础。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

