合理拆分思路通 变式推广规律明
——对2022年一道奥林匹克不等式题的探究
2022-11-25 01:49:27朱斌
中学数学月刊 2022年8期
朱 斌
(南京师范大学第二附属高级中学 320900)
1 赛题与证明
2022年第48届俄罗斯数学奥林匹克联邦区域竞赛中有一道不等式试题:
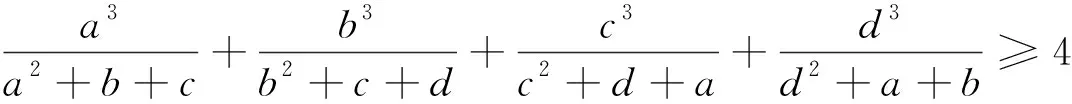
不等式①是一个分式不等式,每个分式项的分子都是一个三次单项式,分母含有三项,前面一项是一个二次单项式,后面两项都是一次单项式.分子、分母中都含有相同的变量.由此入手进行拆项处理,则可打开解题思路.

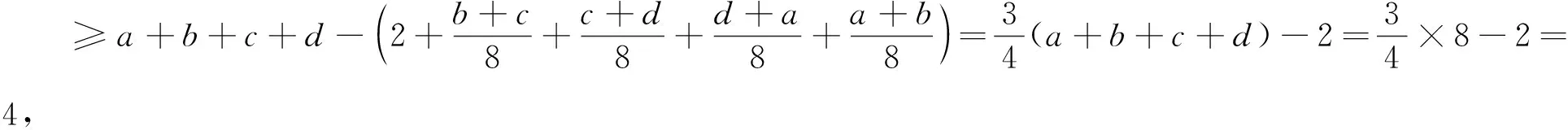
点评如果按照不等式①的结构联想到柯西不等式,将不等式①转化为
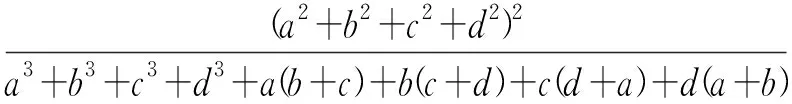
2 变式与推广
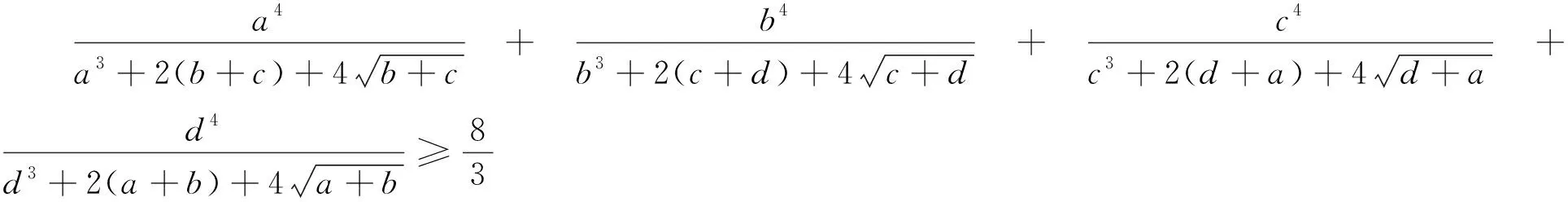
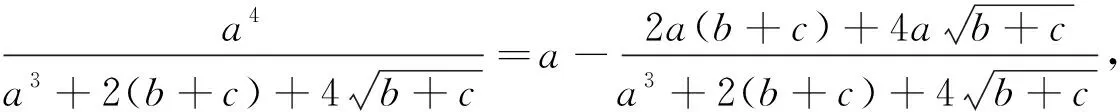
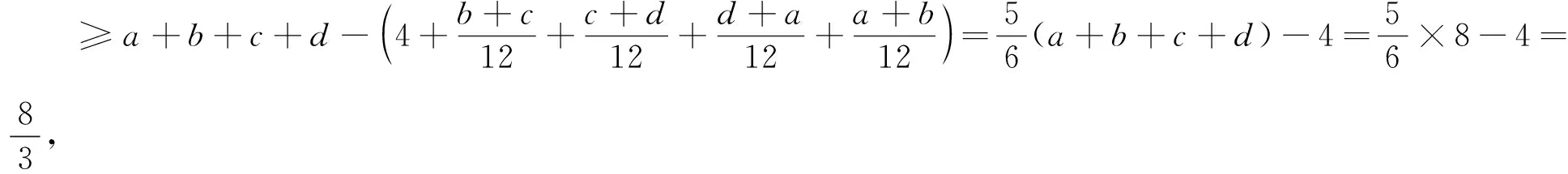
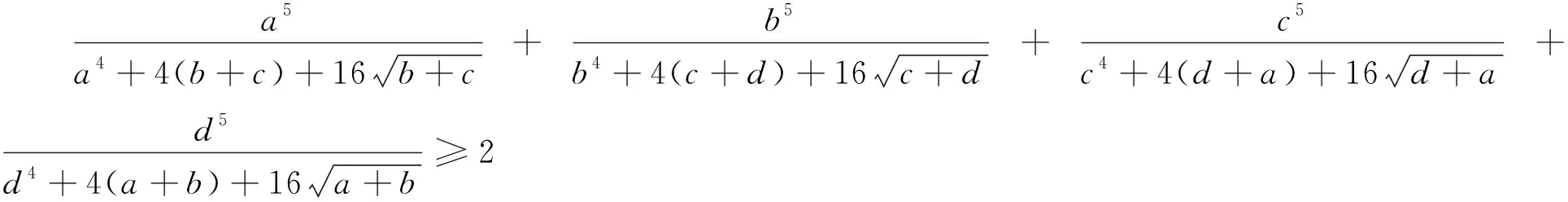
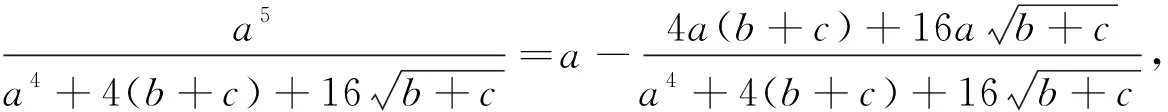
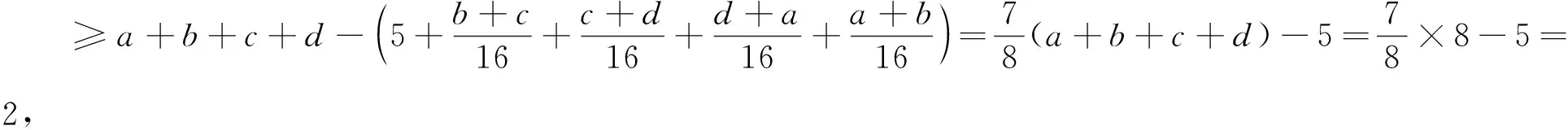
在变式1和变式2的基础上,可以将上述竞赛题作如下推广:
推广1设a,b,c,d为非负实数,有a+b+c+d=8,n∈N*,证明:
证法类似,留给读者完成.
如果改变已知条件中的等式,那么用同样的方法可以证明:
推广2设a,b,c,d为非负实数,有a+b+c+d=4k,k>0,n∈N*,证明:
猜你喜欢
中等数学(2022年4期)2022-08-29 06:27:14
中等数学(2020年7期)2020-11-26 08:03:46
中等数学(2020年4期)2020-08-24 08:08:38
中等数学(2019年5期)2019-08-30 03:52:22
中学生数理化·七年级数学人教版(2018年12期)2019-01-31 02:38:46
中学生数理化·中考版(2017年3期)2017-11-09 02:07:32
中学生数理化·七年级数学人教版(2017年12期)2017-04-18 11:22:02
中学生数理化·七年级数学人教版(2017年12期)2017-04-18 11:22:01
中学生数理化·七年级数学人教版(2016年10期)2016-12-22 18:49:12
初中生世界·七年级(2015年4期)2015-09-10 07:22:44

