水泵水轮机全特性曲线对抽水蓄能电站机组过渡过程的影响

刘 君

(中国电建集团西北勘测设计研究院有限公司，西安 710065)

0 前 言

与常规机组相比，可逆式机组运行工况多且工况转换复杂，因此抽水蓄能电站水力过渡过程比较复杂。尤其是中高水头的水泵水轮机全特性具有明显的反“S”型不稳定区[1]，会对输水发电系统的压力、转速等控制性参数产生较大影响。在抽水蓄能电站输水发电系统的调节保证设计中，从预可研、可研、招标设计阶段，由于机组生产厂家尚未确定，工程设计人员是无法获得真机模型转轮全特性曲线的，因此工程上广泛采用的做法是根据电站发电水头、抽水扬程及负荷的工作范围，套用水头、扬程或者比转速相近的已建电站模型转轮全特性曲线，以此作为过渡过程计算的机组边界条件。对于不同型号的水泵水轮机来说，由于主机厂的技术水平、技术特点、经验积累、水力设计理念和研发重点等不尽相同，其过流通道和转轮的设计存在一定区别，其特性曲线也不一样，这必然会给过渡过程的计算结果带来偏差，偏差甚至会影响工程布置方案的经济性或技术可行性[2-3]。本文结合新疆阜康抽水蓄能电站，分别选取不同的模型转轮全特性曲线，对大波动过渡过程、水力干扰过渡过程和小波动过渡过程进行计算及比对，分析不同机组全特性曲线对抽水蓄能电站水力机组过渡过程的影响。

1 水泵水轮机节点控制方程描述

1.1 工程概况

新疆阜康抽水蓄能电站为Ⅰ等大(1)型工程，装机容量1 200 MW，装有4台单机容量为300 MW的混流可逆式机组，电站额定水头484 m。电站枢纽由上水库、下水库、输水系统和地下厂房等4部分组成。输水发电系统布置于上下水库之间的雄厚山体内，主要由上库侧式进/出水口、上库事故闸门井、上游阻抗式调压室、压力引水主洞、钢衬引水支洞、尾水支洞、尾水隧洞、下库事故闸门井和下库侧式进/出水口等建筑物组成，引水系统、尾水系统均为一洞两机布置。

1.2 全特性曲线处理

水泵水轮机具有发电和抽水两种运行工况，为了将这两种工况统一求解，并避免插值计算中可能产生的多值问题，特对水泵水轮机全特性曲线作如下转换处理[4]：

(1)

(2)

其中

(a≥0)

(a<0)

1.3 转轮边界水头平衡方程

设转轮上、下边界节点编号为1、2，可得到转轮边界水头平衡方程为：

(3)

公式(3)中：CP、CM为特征方程系数，满足正向方程和反向方程；RP、RM为水头损失系数；Hr和Qr分别为额定工况转轮的工作水头和流量，m 和m3/s。

1.4 机组转动力矩平衡方程

α=α0+[(β+β0)-(βg+βg0)]Δt/2Tα

(4)

公式(4)中：Tα为机组惯性时间常数，s；nr、Mr分别为额定工况机组转速和动力矩，r/min和 kN·m；βg为机组转动阻力矩无量纲值；α0、β0、βg0分别为α、β、βg的前一计算时间步长的值。联列上式并结合给定的导叶运动规律y=y(t)，即可求出各种工况的水泵水轮机节点的瞬态参数h、β、α、q等。

2 水泵水轮机全特性曲线的选取

针对阜康抽水蓄能电站的机组水头、扬程范围及机组特性，可研阶段选用国内已建的3个抽水蓄能电站真机模型转轮全特性曲线进行过渡过程计算及对比，这4个抽蓄电站的机组特征参数对比见表1所示。所选的3个抽蓄电站分别称为A电站、B电站和C电站，所对应的真机模型转轮全特性曲线分别称为A曲线、B曲线和C曲线，水头扬程范围涵盖阜康抽蓄电站的水头扬程范围，并且这3个已建抽蓄电站的主机厂家各不相同。对3种模型转轮全特性曲线进行数据离散化处理后，将流量全特性和力矩全特性绘制在同一张图上进行对比，如图1所示。

表1 阜康抽蓄电站与所选3个抽蓄电站的机组参数对比

图1 A、B曲线与C曲线的全特性对比

由图1可以看出，A曲线的满开度单位流量比B曲线和C曲线大，而且在水轮机制动工况区和反水泵工况区的反“S”曲率相对较大；在这3种曲线中，B曲线的反“S”曲率相对较平缓。从3种转轮的水力设计制造厂家来说，A转轮和C转轮均采用的是欧洲水力设计技术，B转轮采用的是日本水力设计技术。在我国已经投运的抽水蓄能电站中，日本可逆式机组水力设计技术与欧洲可逆式机组水力设计技术存在着一定的不同，各具有特色或侧重点[5]。日本可逆式机组的水力设计侧重发电工况的水力性能，对于同一目标电站，在比转速相近的条件下，转轮出口直径较大，转轮总体尺寸较高，流道尺寸偏向于水轮机，其水力性能的优点是反“S”区特性相对较小，但水泵扬程曲线较平，抽水工况入力较大，流量-扬程曲线的“驼峰”性能一般；而欧洲可逆式机组的水力设计侧重抽水工况的水力性能，对于同一目标电站，在比转速相近的条件下，转轮出口直径较小，转轮总体尺寸偏小，其优点是抽水工况性能较好，水泵扬程斜率适中，入力适中，具有较好的流量-扬程驼峰裕度，但其反“S”区曲率相对略明显。

3 大波动过渡过程分析

3.1 不同特性曲线对大波动计算极值的影响

采用一段直线关闭规律，分别采用3种特性曲线对阜康抽水蓄能电站进行大波动过渡过程计算。采用同一水力设计技术的A曲线和C曲线计算结果差距不大，以下重点比较代表两种不同水力设计技术的A曲线与B曲线计算结果，其中这两条曲线的反“S”区特性对比如图2所示。计算结果表明，A曲线的蜗壳末端最大压力、尾水管进口最小压力、输水系统最小压力、调压室涌浪均比B曲线计算结果差，但机组转速上升率优于B曲线。对于蜗壳末端最大压力，两种曲线的最大极值差为27.08 m，尾水管进口最小压力极值差为2.74 m，转速最大上升率极值差为2.34%，输水系统最小压力极值差为2.96 m，调压室最高涌浪极值差为0.55 m，调压室最低涌浪极值差为0.63 m。两种曲线对过渡过程影响较为明显的是蜗壳末端最大压力。由于抽蓄机组发电工况甩负荷时，工况点运行轨迹线不可避免的要通过反“S”区[6-8]，因此以上压力极值的差别主要是由于两种曲线的反“S”区不同造成的。有文献[9]以天荒坪抽蓄为例，人为的将反“S”区的曲线形态及数值做了四种改动，从弯曲明显的“Z”型逐步过渡到弯曲较小的“幺”型，其计算结果表明这种变化对转速最大上升率的影响为3%～5%，对蜗壳最大压力的影响最大为8%，即约60 m的变化范围。

图2 A曲线与B曲线的反“S”区特性对比

3.2 不同特性曲线对水泵工况计算结果的影响

选取典型水泵工况(上库死水位2 237.00 m，下库正常蓄水位1 775.00 m，一台机泵工况抽水断电，导叶正常关闭或拒动)，分别采用B曲线和C曲线进行计算，其对比结果见表2所示。在水泵工况导叶正常关闭时，对于蜗壳末端最大压力，C的计算结果大于B曲线，最大差值约26.63 m；对于尾水管进口最小压力，C曲线的计算结果小于B曲线，最大差值约11.24 m；对于调压室涌浪，两个曲线计算结果较为接近。在水泵工况导叶拒动时，对于蜗壳末端最大压力，C的计算结果略小于B曲线，最大差值约1.6 m；对于尾水管进口最小压力，C的计算结果大于B曲线，最大差值约8.09 m；对于调压室涌浪，两个曲线计算结果较为接近。在水泵工况导叶关闭过程中，工况点的轨迹线穿过水泵工况区、水泵制动工况区、水轮机工况区和水轮机制动工况区，最终到达零开度线上，不同曲线对水泵工况的大波动过渡过程结果存在明显影响。但由于水泵工况下的初始流量小于水轮机工况，在导叶关闭规律合适的情况下，其大波动结果一般优于水轮机工况。

3.3 甩负荷导叶正常关闭工况的控制性参数随时间变化过程对比

以1号机组为研究对象，对发电甩负荷导叶正常关闭工况下的3种特性曲线过渡过程计算结果及变化过程进行对比。选取工况如下：上库正常蓄水位2 271.00 m，下库正常蓄水位1 775.00 m，同一水力单元1台机组正常运行，1台机组启动增至额定功率，在调压室达到最高涌浪的不利时刻，2台机组突甩全负荷，导叶正常关闭。3种特性曲线下的流量变化如图3所示。由于转轮特性曲线存在一定差异，故对于选取的工况来说，组合工况的甩负荷时间点略存在差异，但3者的初始流量几乎一致。3种机组特性曲线的主要控制性参数计算结果对比见表3所示，大波动控制性参数过渡过程变化对比如图4所示。从图3～4中可以看到，机组甩负荷后导叶关闭，随导叶开度减小，流量减小，机组转速升高，工况点轨迹线穿过飞逸线进入水轮机制动工况区，甚至短暂地进入反水泵工况区。在发电工况甩负荷导叶关闭过程中，由于水流的惯性作用，在蜗壳、压力引水管道产生了正水击压力，在尾水管、尾水压力管道产生了负水击压力，调压室水位也产生了大幅度的上升和下降，随后在上下游水库、调压室、水泵水轮机、岔管等边界反射作用下，产生压力振荡和水位波动[10]。3种曲线的调压室涌浪极值差距不大，蜗壳末端最大压力存在较大的差别；大波动参数的趋势变化大体上一致，但极值发生时刻和局部变化过程存在一定差异，其中尾水管压力的极值附近震荡变化过程差异较为明显。

图3 3种曲线的机组过流量随时间变化过程对比

表2 不同特性曲线下抽水工况过渡过程计算结果对比

图4 3种曲线的大波动控制性参数随时间变化过程对比

3.4 甩负荷导叶拒动工况的控制性参数随时间变化过程对比

以2号机组(拒动机组)为研究对象，对发电甩负荷导叶拒动工况下的3种特性曲线过渡过程计算结果及变化过程进行对比。选取工况如下：上库设计洪水位2 272.25 m，下库死水位1 743.00 m，最大水头，额定功率，同一水力单元2台机同时甩全负荷，导叶一关一拒。3种特性曲线下的流量变化如图5所示。3种机组特性曲线的主要控制性参数计算结果对比见表4所示，大波动控制性参数过渡过程变化对比如图6所示。发电工况甩负荷后，导叶拒动的机组运行工况点将沿等开度线移动，经过水轮机工况区、水轮机制动工况区，甚至进入反水泵工况区，最后终止在飞逸工况线上周期性地发生倒流，从图5～6中可以看到，机组流量、压力、转速将作周期性振荡，此时实际工程中必须紧急关闭进水球阀，避免事故进一步恶化。在导叶拒动时，由于本工程上、下游输水系统较长，虽然导叶拒动不关，但由于高水头水泵水轮机转轮的“截止效应”，在上、下游输水系统中仍产生了很大的正水击和负水击，如A曲线下的蜗壳末端最大压力为750.97 m，尾水管最小压力为20.46 m，均接近本电站的过渡工程计算控制值。在导叶拒动工况下，由于3种曲线的过流特性差异，蜗壳末端压力和尾水管进口压力的极值差别达到最大，其中蜗壳压力极值的最大差值为34.53 m，尾水管进口最小压力极值的最大差值为15.68 m；大波动参数的趋势变化基本一致，但波峰和波谷极值存在明显差异。

表3 典型工况下3种曲线的大波动过渡过程计算结果对比

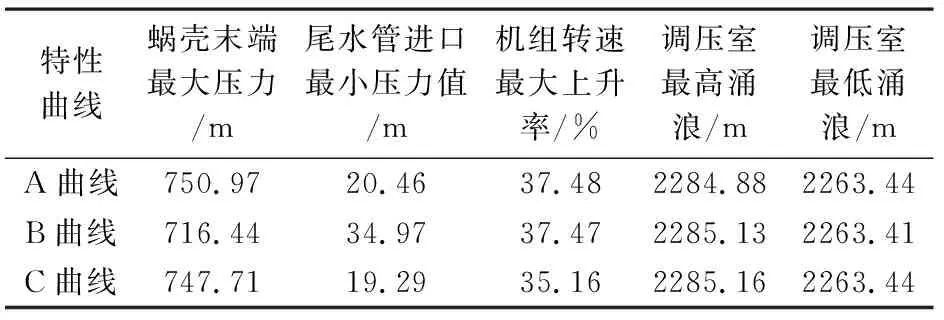
表4 典型工况下3种曲线的大波动过渡过程计算结果对比

3种机组特性曲线的大波动控制性参数极值过渡过程变化对比如下。

图5 3种曲线的机组过流量随时间变化过程对比

4 水力干扰过渡过程分析

分别采用B曲线和C曲线对水力干扰过渡过程进行计算及对比。当采用B曲线时，机组联入无穷大的电网条件下的开度调节中，机组功率摆动幅度最大为28.52%，调压室涌浪向上和向下最大振幅分别为7.76 m和6.1 m；功率调节中，机组出力摆动幅度最大为28.78%，调压室涌浪向上和向下最大振幅分别为8.09 m和6.34 m。机组联入有限电网的频率调节中，机组进入±0.2%带宽的调节时间为298 s，发生工况为“额定水头，同一水力单元的两台机组额定功率正常运行时，其中一台甩负荷，导叶正常关闭”。当采用C曲线时，机组联入无穷大的电网条件下的开度调节中，机组功率的摆动幅度最大为33.69%，调压室涌浪向上和向下最大振幅分别为8.07 m和6.56 m；功率调节中，机组出力的摆动幅度最大为37.33%，调压室涌浪向上和向下最大振幅分别为8.07 m和6.49 m。机组联入有限电网的频率调节中，机组进入±0.2%带宽的调节时间为228.8 s，发生工况为“额定水头，同一水力单元的两台机组额定功率正常运行时，其中一台甩负荷，导叶正常关闭”,以及工况“最小水头，同一水力单元的两台机组额定功率正常运行时，其中一台甩负荷，导叶拒动”。

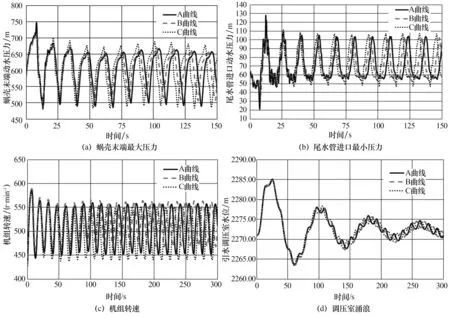
图6 3种曲线的大波动控制性参数随时间变化过程对比

在开度调节和功率调节下对比B曲线和C曲线的水力干扰过渡过程计算结果，采用C曲线的功率摆动幅度大于B曲线；在频率调节模式下，C曲线进入±0.2%带宽的调节时间小于B曲线，振荡次数和超调量小于B曲线，只有最大偏差略大于B曲线。不同曲线对水力干扰的影响差别较为明显，但2种曲线下的机组出力均呈收敛趋势。机组转速波动比小波动过渡过程剧烈，调节时间较长，但转速波动总趋势均是收敛的。计算中还发现干扰机组的增甩负荷时间对结果存在明显影响。一般来说，实际管道中水击波比计算值衰减要快，因此实际出力摆动会低于计算值。

5 小波动过渡过程分析

选取同一套调速器参数，分别采用B曲线和C曲线对孤立电网下的小波动过渡过程进行计算及对比。当采用B曲线时，小波动最大调节时间出现在工况“额定水头，两台机组满功率运行，突减10%负荷”，此时进入±0.2%带宽的调节时间为23.8 s，最大偏差为13.62 r/min，振荡次数为0.5，衰减度为0.97，超调量为0.03。当采用C曲线时，小波动最大调节时间出现在工况“额定水头，两台机组80%功率运行，突减10%负荷”，此时进入±0.2%带宽调节时间为24.6 s，最大偏差为12.33 r/min，振荡次数为0.5，衰减度为0.94，超调量为0.06。对比B曲线和C曲线的小波动过渡过程计算结果，调节时间均很短，调节品质较好，两者差距很小。

6 结 论

(1) 水泵水轮机全特性曲线中存在开度线交叉和聚集现象的反“S”区，目前对全特性曲线的离散主要是基于SUTER法的无量纲处理方法，该处理方法的应用已比较成熟，因而不同水泵水轮机全特性曲线造成的计算结果差异主要是由转轮本身过流特性造成的。不同水力设计技术的水泵水轮机曲线带来的计算结果差异较为明显，在抽水蓄能电站前期的调节保证设计中，机组尚未招标，应充分重视相似全特性曲线的选择。

(2) 不同水力设计的转轮全特性曲线对水泵工况大波动过渡过程结果存在明显影响，但由于水泵工况初始流量小于水轮机工况，在导叶关闭规律合适的情况下，其大波动结果一般优于水轮机工况。在机组甩负荷且导叶拒动工况下，不同水力设计的特性曲线中，大波动控制性参数的趋势变化基本一致，但波峰和波谷极值存在明显差异，蜗壳末端压力和尾水管进口压力的极值差别达到最大。

(3) 不用水力设计的转轮曲线下小波动计算结果差异较小，但水力干扰计算结果存在明显差异。水泵水轮机全特性曲线尤其是反“S”区的曲率变化对输水发电系统压力、机组转速等大波动控制性参数极值产生较大影响，因而减缓反“S”区的曲率是水泵水轮机水力设计的重点问题之一，在转轮水力优化设计中考虑过渡过程的影响是值得深入研究的一个课题。