焊点加速寿命试验模拟

马正刚，夏宗泽

（江苏自动化研究所，连云港 222006）

引言

电子产品封装中焊点在复杂应力作用下会因疲劳发生断裂失效而引发可靠性问题，而焊点的寿命直接影响电子产品的使用寿命。加固计算机等电子装备实际工作环境严苛，环境应力复杂多变，在持续热循环载荷作用下焊点可能会发生疲劳失效，导致电子装备故障。焊点一般由多种材料组成，当温度发生变化时，由于各个材料热膨胀系数不同，导致焊点内部发生不连续应变而引起应力集中现象，材料随着环境的持续加热与冷却，应力状态反复变化直至疲劳，最终导致焊点断裂失效[1]。在加速寿命试验中，试验件承受的温度载荷远超正常工作条件，焊点因疲劳出现断裂失效的概率增加。对于焊点的疲劳寿命预测，一般应用理论方法或有限元法，姜志中[2]研究了焊点在热循环载荷下的失效机理，并采用Coffin-Manson 模型对焊点进行疲劳寿命模拟。

针对焊点内部的疲劳失效问题，本文以加固计算机中封装电路板为研究对象，建立简化的电路板二维轴对称模型，开展焊点加速寿命试验模拟，应用有限元法模拟了焊点内部由热应力导致的应力应变情况，分别利用Coffin-Manson和Morrow寿命模型预测了焊点的疲劳寿命。

1 焊点模型

1.1 焊点模型定义

研究模型使用了电路板的原理图，其包含了模型的主要结构和功能。电路板模型如图1所示。模型包含了芯片、焊点、印刷电路板、以及中间连接件，使用轴对称方法进行建模，PCB板和芯片的尺寸均为2×0.5 mm2，焊点的尺寸为0.5×0.25 mm2。

图1 电路板模型

1.2 材料属性、网格

印制电路板（PCB）是一种玻璃纤维压板结构，焊点材料为SnAgCu合金，计算中假设模型结构处于平面应变状态，所有材料为各项同性，且材料性能不受温度影响[6]。这些材料在热载荷加载中会产生线性和非线性响应，材料参数如表1所示。模型网格采用自由划分的方式，网格类型为自由三角形网格。

表1 电路板各组件材料参数

1.3 边界条件与载荷

1）约束条件

在循环温度应力作用过程中，电路板受固定约束，约束点为PCB板右下角。

2）热循环载荷

热循环载荷作为一种经典的交变温度应力，能够比较准确的模拟出焊点在工作条件下所受到周期性变化的热应力下焊点的应力应变响应。加速寿命试验的热循环载荷：（25～100）℃，高低温保温时间均为15 min，升降温速率为5 ℃/min，一个循环为60 min，温度变化曲线如图2所示。

图2 热循环载荷变化图

2 疲劳寿命模型

采用蠕变模型来研究焊点在温度应力下的疲劳规律，焊点材料的蠕变是非线性的。蠕变是材料的一种特性，蠕变分为初级蠕变、二级蠕变、三级蠕变三个阶段，各阶段下蠕变速率不同，二级蠕变过程又称稳态蠕变，因为恒定应力下应变速率不变。如图3所示，恒定应力下材料的蠕变随时间不断变化，蠕变应力逐渐增加。

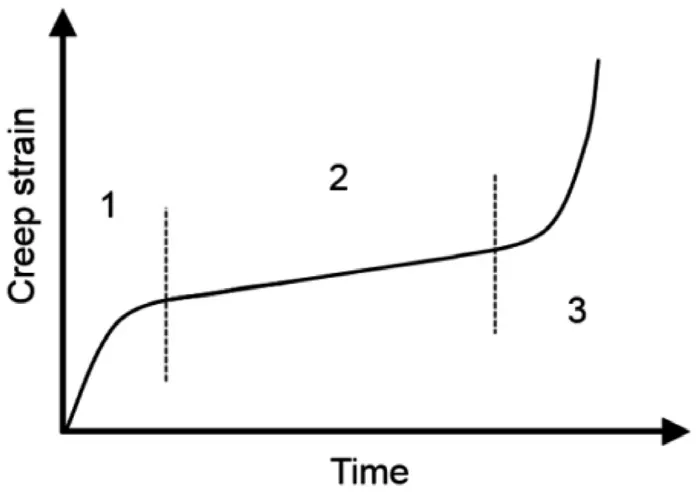
图3 恒定应力下材料蠕变变化趋势

控制模型选择双牛顿蠕变方程，模拟焊点在稳定蠕变状态下的疲劳寿命，不考虑材料的初级蠕变和三级蠕变过程，控制方程如下。

式中：

σe—等效应力；

AⅠ，nⅠ，AⅡ，nⅡ，σn—材料常数，参数值如表2所示。方程第一项表示低应力值下的蠕变速率，第二项表示高应力值下的蠕变速率。

表2 材料常数

3 结果分析

由蠕变激励引起的非线性材料疲劳试验是一个长耗时过程，在加速寿命试验中，通过将材料置于远超正常试验的条件下来大大缩短试验时间。当求解非线性材料的疲劳寿命时，通过模拟一个循环就可以获得稳定循环状态。计算得到材料的等效蠕变应力曲线，如图4所示。焊点的等效蠕变应力值是低应力和高应力值下两种蠕变应力的总和，一个温度循环中，等效蠕变应力值主要以高应力值下蠕变为主，低应力值下的蠕变应力较小。

图4 焊点等效蠕变应力曲线

利用Coffin-Manson和Morrow寿命模型预测焊点的疲劳寿命，其分别是基于应变和基于能量耗散来计算疲劳寿命，结果如图5和图6所示。两种预测模型下，焊点的疲劳寿命结果分别为907和625个循环数，临界点均位于左上角，焊点的左上角在循环温度载荷下是最先失效的地方。不同的控制模型下，由于模型参数存在差异，预测结果有所差别。

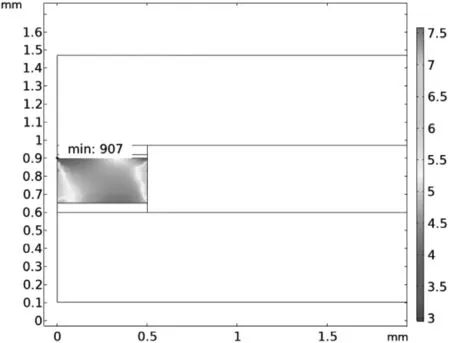
图5 基于应变模型的疲劳寿命

图6 基于能量耗散的疲劳寿命

4 结论

1）循环温度应力加载下的加速寿命试验中，焊点的蠕变等效应力主要以高应力值下蠕变应力为主，低应力值下的蠕变应力较小；

2）焊点在（25～100）℃的循环温度应力作用下，基于应变控制（Coffin-Manson）和能量耗散控制（Morrow）的疲劳寿命分别为907和625个循环，两种结果中焊点的临界点均位于左上角，在加速寿命试验中焊点左上角是最先失效。