飞机关键部位湿热环境内外场相似性研究

邓文亮，吴敬涛，成竹，唐扬刚

（中国飞机强度研究所，西安 710000）

引言

飞机着陆后要逐渐减速到低速状态，以滑行到指定的位置，可以使飞机减速的方式有三种：其一是通过安装在起落架上的机轮刹车系统，飞行员控制刹车系统工作，使安装在机轮上的刹车盘相互挤压而产生摩擦力，以此来使飞机减速。在刹车盘的作用下，将飞机滑行时的动能转化为热能，以自然冷却或者强制冷却的形式散热。这种制动方式效率高，安全可靠。其二是发动机开启反推装置。通过安装在飞机发动机上的反推装置，改变发动机燃气的喷射方向，产生与飞机前进方向相反的力，使飞机得以减速。第三种方法是通过安装在飞机机身以及机翼上的扰流板，使用时向外张开以增大空气阻力，也可以达到减速的目的，这种方法在飞机滑行速度较高时效果比较好。第二种和第三种减速方式受环境温湿度因素影响较小，湿热的外场环境不足以产生明显的影响。机轮刹车方式由于其制动力全部来自于刹车盘之间的摩擦作用，刹车盘的摩擦力直接关乎制动力的大小。根据摩擦力的计算公式f=μF，其中μ为滑动摩擦系数，F为正应力，在刹车系统提供的正应力一定的条件下，刹车盘提供的摩擦力与其滑动摩擦系数成正比，目前碳/碳复合材料制成的刹车盘因其优异的耐磨性和散热性得到了大量应用。停放在外场的飞机，由于温湿度的改变，其刹车盘的摩擦系数也会发生变化，进而导致了飞机的制动距离与预期的偏差。

本文开展了湿热环境试验相似性表征与准则研究，进行了湿热内外场环境试验，通过典型工况的外场环境稳态响应与实验室环境稳态响应测量数据对比分析，研究了刹车材料湿热环境下的摩擦系数的拟合方法，基于合适的拟合方法对湿热内外场环境试验相似性进行了研究，通过基于内场拟合曲线的缩放变换的方式，较好地将内场拟合曲线变换为外场拟合曲线，从而得到飞机关键部件湿热环境试验相似性表征方法，并提出了相似性准则。

1 理论分析

通过基于BP神经网络的摩擦系数模型，利用反向传播来调整网络的权值和阀值，使网络误差的平方和最小。BP神经网络具有强大的非线性映射能力和泛化功能，任一连续函数或映射均可采用3层网络加以实现。网络结构如图1所示。

图1 BP神经网络结构示意图

在飞机刹车过程中，刹车力矩和刹车盘摩擦系统是相互耦合，互相影响，刹车温度、飞机速度处于变化状态，刹车盘摩擦系数、刹车力矩也是变化的。由于刹车盘摩擦系数的影响因素主要包括刹车盘温度、刹车力矩和刹车机轮速度，因此建立以刹车盘温度（℃）、刹车力矩（Nm）、机轮速度（m/s）为输入，以摩擦系数为输出的神经网络结构，以确定任意条件下的摩擦系数。

采用三层BP网络结构[1]，各层输入与输出关系为：

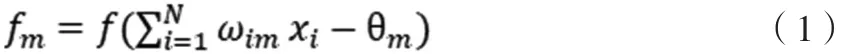
式中：

N—隐含层个数xi（i=1，2，…，N）为输入信号；

θm—阈值；

ωim—从神经元m到神经元i的连接权值。

输入参量：

式中：

T —刹车盘温度；

P—刹车力矩；

v—机轮速度。

2 实验设计与装置

2.1 试验装置

为了研究湿热外场环境对刹车盘刹车材料摩擦系数的影响，参考GB-10006，设计了刹车盘刹车材料湿热环境摩擦系数测试实验，在外场试验中，将刹车材料置于外场环境中保持一段时间，使试样与外场环境的温度和湿度达到稳态，然后使用摩擦系数测试仪测量刹车材料在当前所处环境下的摩擦系数。进行内外场试验使用ZJ-MC02型摩擦系数测试仪，测试精度为0.05 %FS，如图2所示，该摩擦系数测试仪主要由水平试验平台、滑块、驱动机构及测力系统构成，其中水平试验台由平整的非磁性材料制成，平台上嵌有用于调整水平状态的水平泡，滑块用于装载试样，驱动机构可以带动滑块匀速运动，速度可以在0～500 mm/min之间无级调节，测力系统可以测出拉动滑块的力，用于计算摩擦系数。

图2 ZJ-MC02型摩擦系数测试仪

2.2 摩擦材料试样

实验材料为用于飞机刹车盘制造的碳复合材料，为了便于实验过程中摩擦系数的测量，参考GB-10006对试样材料进行了加工处理，其中用于摩擦的下试样加工尺寸（长×宽×高）为133×63×7 mm，上试样的加工尺寸（长×宽×高）为63×63×7 mm，试验材料及试样如图3所示。

图3 试验材料及加工好的试样

2.3 实验过程

在珠海以及上海进行了湿热环境下刹车盘刹车材料摩擦系数测试试验，试验温度范围（29.3～39.3）℃，在正式试验前进行了预实验，为可能出现的问题制定预案。试验开始前先将试验平台调至水平状态，调整设备使其处于正常工作状况下。因外场环境温度和湿度处于波动状态中，故每次测试中记录三次温度和湿度数据。

3 内外场实验数据处理与分析

在外场试验中，进行了温度（29.3～39.3）℃范围内共32组有效试验，包含外场试验动摩擦系统测试和静摩擦系统测试，内场试验中，进行了（50～90）%湿度范围内的试验，每种湿度工况下测量了（31～39）℃五种温度下的摩擦系数，包含外场试验动摩擦系统测试和静摩擦系统测试。在外场试验中，温度和湿度随着环境的变化而变化，为了便于数据的拟合，找寻内外场试验之间的相似性，采取控制变量的办法先对数据进行选择。以动摩擦系数为例，将湿度控制在70 %左右，温度作为自变量，截取出内外场试验的部分数据，以此数据研究温度对动摩擦系数的影响；然后将温度控制在35 ℃左右，以湿度为自变量，研究湿度对动摩擦系数的影响。通过研究温度和湿度对动摩擦系数的影响，进行内外场试验的相似性研究。

3.1 内外场试验数据拟合方法一

以温度为自变量的内外场动摩擦系数试验数据如表1所示。

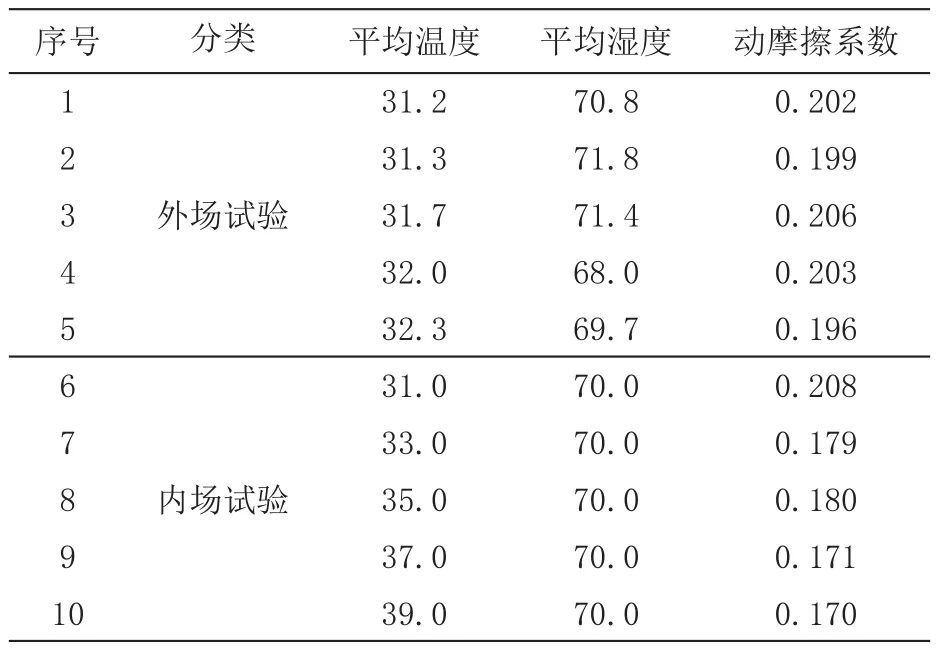
表1 材料动摩擦系数内外场试验部分数据

为了研究摩擦系数内外场的相似性与相似性表征方法，选择合适的拟合曲线进行拟合，以拟合优度作为评价指标，在尝试过多种拟合模型之后，选择指数拟合、Gaussian拟合、线性拟合、一次多项式拟合模型对内外场数据进行拟合，拟合情况及拟合优度见表2。

综合分析各拟合模型的拟合优度，见表2，以上四种拟合模型对于内场试验数据的拟合优度尚可，在0.7以上，其中线性拟合的拟合优度最好，在对外场试验数据的拟合中，四种拟合模型的拟合优度出现了两极分化，Gaussian拟合模型以及线性拟合模型因其拟合曲线与试验数据点贴合度较好而拟合优度较高，但其拟合曲线与内场试验数据拟合曲线相似性较差；指数拟合模型以及一次多项式拟合模型因其拟合曲线比较“直”而拟合优度较差，其拟合曲线与内场试验数据拟合曲线在曲线形状上较为接近。

表2 各拟合模型的拟合优度

3.2 内外场试验数据拟合方法二

以湿度作为自变量的内外场动摩擦系数试验数据如表3所示。

表3 材料动摩擦系数内外场试验部分数据

以拟合优度作为评价指标，综合考虑内外场拟合曲线的相似性，选择多种拟合模型进行数据拟合，在尝试过多种拟合模型之后，选择指数拟合、一次多项式拟合以及幂函数拟合模型对内外场数据进行拟合，拟合情况及拟合优度见表4。

综合分析各拟合模型的拟合优度，见表4。根据各拟合模型的拟合曲线，动摩擦系数与湿度呈明显的正相关关系，即随着湿度的升高，动摩擦系数逐渐增大。上述三种拟合模型对于外场试验数据的拟合效果较好，整体高于0.7，其中以幂函数拟合模型的拟合效果最好，对于内场试验数据的拟合，各拟合模型的拟合优度相对较低，其中以幂函数拟合的拟合效果最好。

表4 各拟合模型的拟合优度

4 内外场试验相似性研究

4.1 温度对动摩擦系数的影响

在研究温度对动摩擦系数的影响的过程中，通过选择合适的曲线，对实验得到的散点数据进行相关性拟合，尝试选择平移内外场同类实验的拟合图像，通过选择基于内外场温度实验结果的实验温差，对内场试验拟合曲线进行平移，并通过R2评价研究内场试验拟合曲线平移后与外场试验数据的相似性。平移变换情况及拟合优度记录见表5。

综合分析各拟合模型的平移量与拟合优度，见表5。对比四种拟合模型平移变换拟合优度，其中线性拟合模型拟合优度最好，指数拟合模型拟合优度最差，Gaussian拟合模型对实验数据散点拟合效果较好，对平移变换后的拟合曲线，其拟合表现不佳。从宏观来看，四种拟合模型的拟合效果整体欠佳，这与外场试验数据的分散性有一定的关系。

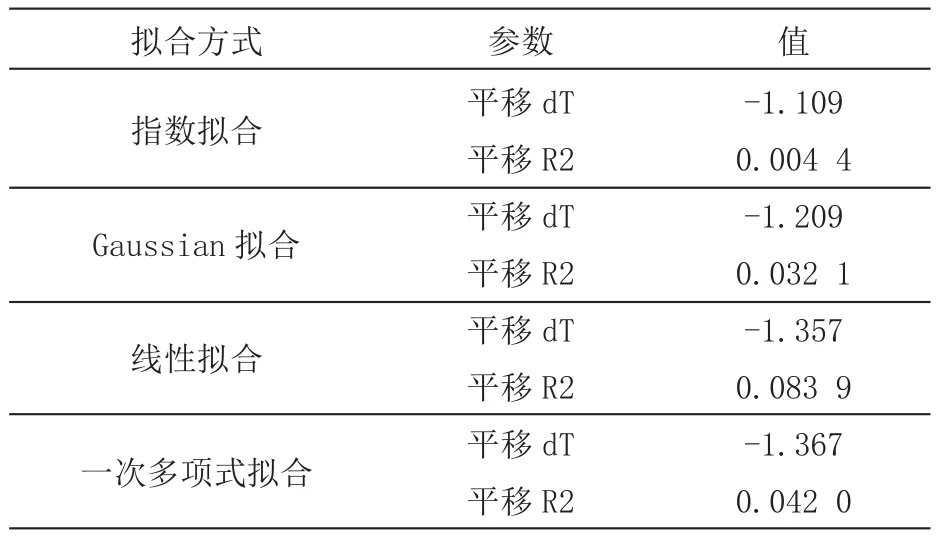
表5 各拟合模型的平移量与拟合优度

4.2 湿度对动摩擦系数的影响

在研究湿度对动摩擦系数的影响的过程中，采取类似的方法，平移内外场同类实验的拟合图像，通过选择基于内外场试验结果的湿度差，对内场曲线进行平移，并通过R2评价研究内场试验拟合曲线平移后与外场试验数据的相似性。平移变换情况及拟合优度记录见表6。

综合分析各拟合模型的平移量与拟合优度，见表6。在内外场试验结果的相似性分析中，采用幂函数拟合模型的内场试验拟合曲线与外场试验拟合曲线在曲线形状上相似性较差，采用平移变换的拟合优度不佳，故在内外场相似性分析中，不采用幂函数拟合模型。根据各模型平移变换的拟合优度，一次多项式拟合模型的拟合优度相对较高，但从整体来看，采用两种拟合模型将内场试验拟合曲线平移，其对外场试验的拟合效果不佳，只在一定程度上可以代替外场试验的效果。

表6 各拟合模型的平移量与拟合优度

5 内外场试验相似性表征方法研究

5.1 温度作为影响动摩擦系数的自变量的表征方法

以温度作为影响动摩擦系数的自变量，根据之前的相似性研究，可以通过对内场试验拟合曲线进行平移变换来近似表达外场试验，为确保试样基于内场曲线的外场导出曲线的精度、曲线特征和相似性，选择缩放平移的方式对曲线进行变换。指数拟合模型进行缩放变换后拟合模型变为：

使经过缩放变换的拟合曲线通过外场数据的部分采样点，或者使用MATLAB进行拟合，通过求解待定系数或者拟合回归的办法，求得推导的外场曲线，解得缩放得到的最大拟合优度时的变化倍率k，平移量dT和拟合优度R2如表7所示，伸缩变换情况如图4（a）所示。

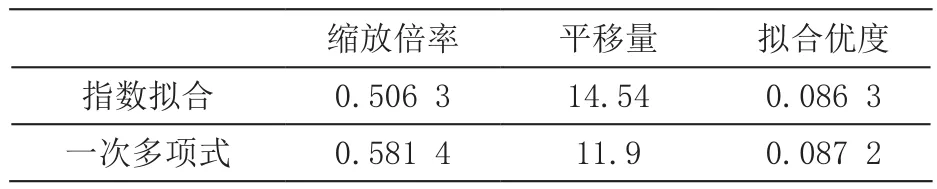
表7 指数拟合伸缩变换情况

对一次多项式拟合模型进行类似的缩放变换处理，得到最大拟合优度时的变化倍率k，平移量dT和拟合优度R2，如表7所示，相应的内外场变换情况如图4（b）所示。

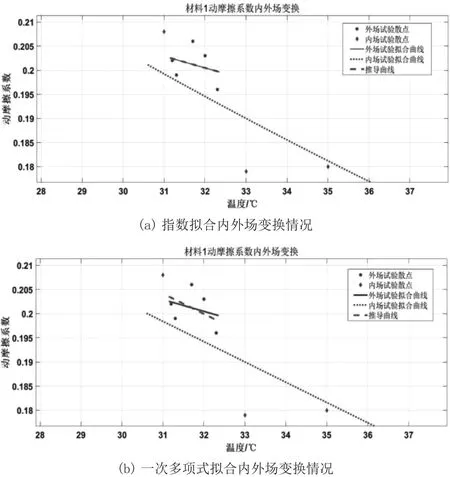
图4 不同拟合方式的内外场变换情况

由表8可以直观地看出，对内场拟合曲线采用缩放变换得到的推导曲线，其拟合优度与通过外场散点直接拟合得到的拟合曲线的拟合优度相等，拟合曲线的形状比较相似，因此可认为这种缩放变换较为合理，成功将内场拟合曲线变换为外场拟合曲线。

表8 不同拟合方式的拟合优度

5.2 湿度作为影响动摩擦系数的自变量的表征方法

以湿度为自变量进行内外场试验的相似性研究，采用缩放平移的方式对内场试验拟合曲线进行变换，使经过缩放变换的拟合曲线通过外场数据的部分采样点，或者使用MATLAB进行拟合，通过求解待定系数或者拟合回归的办法，求得推导的外场拟合曲线，解得缩放变换得到的曲线达到最大拟合优度时的变化倍率k，平移量dT和拟合优度R2如表9所示，缩放变换情况如图5（a）和图5（b）所示。

图5 不同拟合方式的内外场变换情况

由表10可以直观看出，根据缩放变换得到的曲线的拟合优度，指数拟合以及一次多项式拟合模型都有相对较好的拟合优度，拟合优度均高于0.7。将缩放变换得到的曲线与外场散点直接拟合得到的拟合曲线的拟合优度进行对比，采用一次多项式拟合模型时，二者比较接近，当采用指数拟合模型时，二者相等。因此可以认为这种缩放变换较为合理，成功将内场拟合曲线变换为外场拟合曲线。

6 小结

本文对刹车材料摩擦系数的内外场试验进行了相似性研究，根据试验结果可以得到以下结论：

表9 拟合模型缩放变换情况

表10 不同拟合方式的拟合优度

1）在摩擦系数的内外场试验中，相同情况下，内场试验得到的摩擦系数低于外场试验下的摩擦系数，即内场试验相较于外场试验更“严苛”一些。

2）在以温度作为自变量的相似性研究中，当采用指数拟合以及一次多项式拟合模型时，由内场拟合曲线经过缩放变换得到的推导曲线与直接由外场散点拟合得到的外场拟合曲线在拟合优度上比较接近；以湿度作为自变量时，采用缩放变换可以得到相同的效果。因此，这种缩放变换可以在一定程度上将内场拟合曲线变换为外场拟合曲线。