弹性波穿越土工袋传播规律的数值模拟

贾 凡，刘斯宏，程宏旸

(1.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038；2.河海大学水利水电学院，江苏 南京 210098； 3.University of Twente，Enschede 7500AE)

土工袋是一种将土、碎石或建筑废料等装入编织袋中形成的袋装物。作为一种土体加固技术，土工袋已成功应用于房屋地基，公路、铁路路基，堤防，边坡加固及挡墙构筑等工程中。作为一种柔中有韧的结构，土工袋在编织袋的约束作用下具有很高的抗压强度，同时，具有显著的减隔震效果。

相关学者们在土工袋动力特性及减隔震效果方面进行了大量的试验研究。王艳巧等[1-3]开展了土工袋及其袋内材料的振动台试验，对比研究了不同输入振动频率与加速度大小工况下土工袋与其袋内材料的加速度响应情况，试验结果表明，在较高频率输入加速度下，土工袋的减振效果远大于天然河砂。Liu等[4-7]通过一系列水平循环剪切试验、竖向激励试验、小型振动台试验以及土工袋沟槽回填现场试验，对土工袋动力特性进行了研究，结果表明，土工袋具有相对较高的阻尼比和可变的水平刚度。Ding等[8]通过一系列的室内试验，分析了在施加交通荷载时土工袋路基的动力特性，结果表明，峰值加速度随着距振动源深度的增加而线性减小，土压力的衰减随着与振动源距离的增加而增加；Liu等[9]采用竖向重复荷载试验研究了土工袋在道路路基中的加固性能以及荷载频率和振幅、加固层数等对加固性能的影响，结果表明，土工袋作为加固材料可以有效减少路基的变形与交通荷载引起的振动。

离散单元法[10](discrete element method，DEM)是岩土工程中一种常用的数值计算方法，可用于探索由颗粒层面相互作用引起的宏观现象。王艳巧等[11]采用DEM进行了土工袋减振消能的数值模拟，从能量角度解释了土工袋的减振效果，结果表明，土工袋的能量耗散随着加、卸载循环过程的进行而呈现波浪式增减；Cheng等[12]采用DEM对土工袋在单剪试验条件下的应力状态和各向异性进行了数值模拟，较好地分析了土工袋加固地基方法的机制和效果，即变形限制和结构互锁；Jia等[13]采用DEM进行了竖向循环荷载作用下土工袋的数值模拟，验证了考虑土工袋张力和竖向应变之间关系的土工袋强度预测公式。

DEM也可用于模拟弹性波在颗粒介质中的传播过程。本文采用商业软件PFC3D对土颗粒地基模型与埋设单层土工袋的土颗粒地基模型进行弹性波传播的数值模拟，研究地基中土工袋对弹性波波速及地基阻尼比的影响，初步探索弹性波穿越土工袋的传播规律。

1 DEM数值模拟

1.1 接触模型

在DEM中，两个粒子之间或者一个粒子和一个边界的接触，都可模拟为在法向和切线方向上的一个弹簧和阻尼器模型。在法向上，颗粒之间可以互相重叠产生压力；在切线方向上，如果切向力达到库仑摩擦极限，则产生滑动。颗粒间的接触力通过赫兹模型[14]的力-位移规律进行计算：

Fn=hngc1.5

(1)

(2)

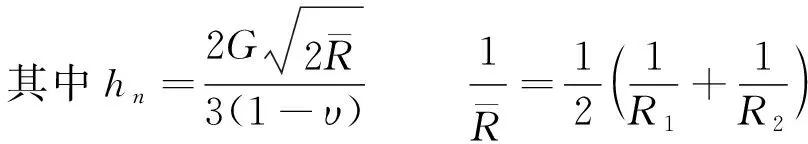
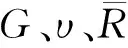
在传统的接触模型中，粒子之间的力仅在它们接触时才产生，法向弹簧具有无拉力约束。显然，该模型并不适用于柔性编织袋，因为编织袋只能承受拉力作用而不能受压。本文将柔性编织袋模拟为一系列通过平行黏结模型相连的等径圆形颗粒[15]。当两个相邻编织袋颗粒之间的距离拉长时会产生拉力，该拉力根据拉长的距离和弹簧的刚度来计算。平行黏结强度对应于在弹性范围内的编织袋抗拉强度，由拉伸试验确定，如图1所示。根据拉伸试验结果，经试算率定出编织袋颗粒间的拉伸刚度为5 MPa，拉伸强度为5.2 MN/m。

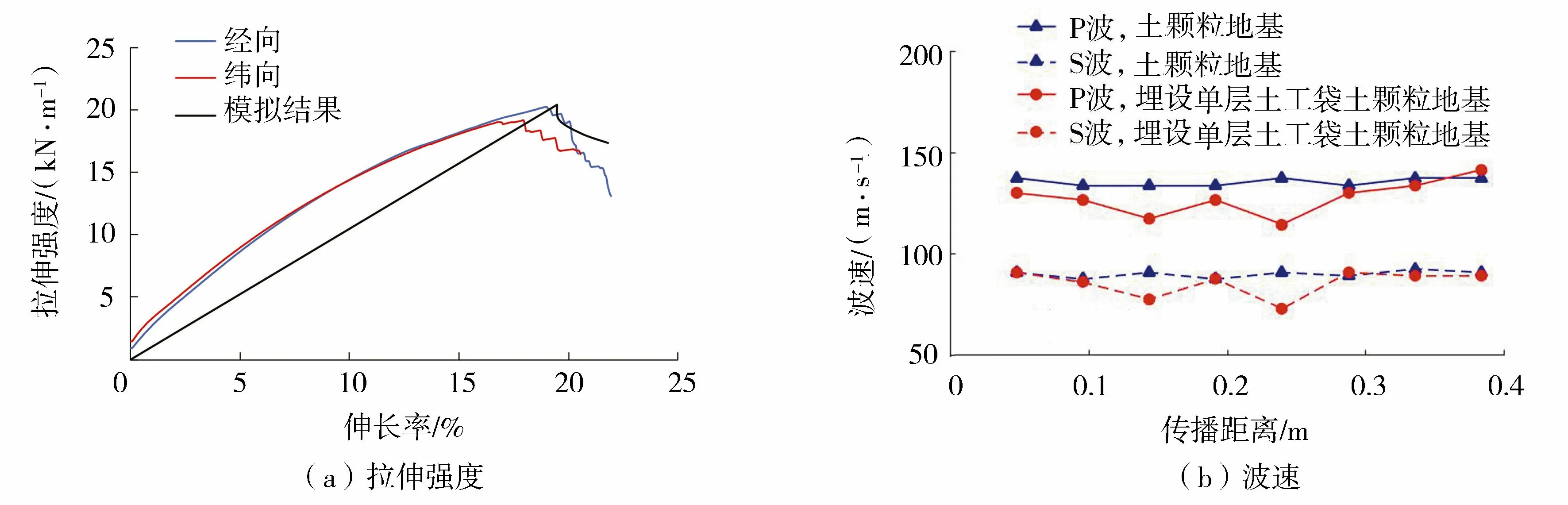
图1 土工编织袋拉伸试验与数值计算结果对比Fig.1 Comparison of tensile test and numerical calculation results of woven soilbag

1.2 模型构建

为了探究土工袋界面对弹性波的反射干扰效应，分析土工袋对土体中弹性波传播的影响，分别建立了初始条件与边界条件相同的土颗粒地基模型与埋设单层土工袋的土颗粒地基模型，如图2所示。土颗粒的粒径在2.4 mm与6 mm之间均匀分布，平均半径为4 mm。土颗粒地基模型有137 365个颗粒，埋设单层土工袋的土颗粒地基模型共145 336个颗粒。首先在立方周期性边界中按设定的颗粒粒径范围随机生成松散试样，使用各向同性压缩方法[16]，通过将颗粒接触摩擦设为0，可以得到致密状态(孔隙比为0.3)。为了消除试样生成过程中不平衡力引起的干扰，继续执行若干计算步，直到颗粒所受不平衡力的平均值与所施加力和体积力平均值之比小于10-8[17]。在试样水平方向上使用周期性边界以消除波传播期间的边界效应，如图2所示。固定试样底部和顶部的颗粒(紫色和绿色)，以避免上下两端颗粒穿透边界互相影响。土工袋横截面形状为正方形，纵截面形状为两侧半圆形的长条形状，四角处以两圆柱相贯线的形式连接，其纵切面如图2(b)蓝色部分所示，地基及袋内土体的级配与计算参数与砂土地基相同。

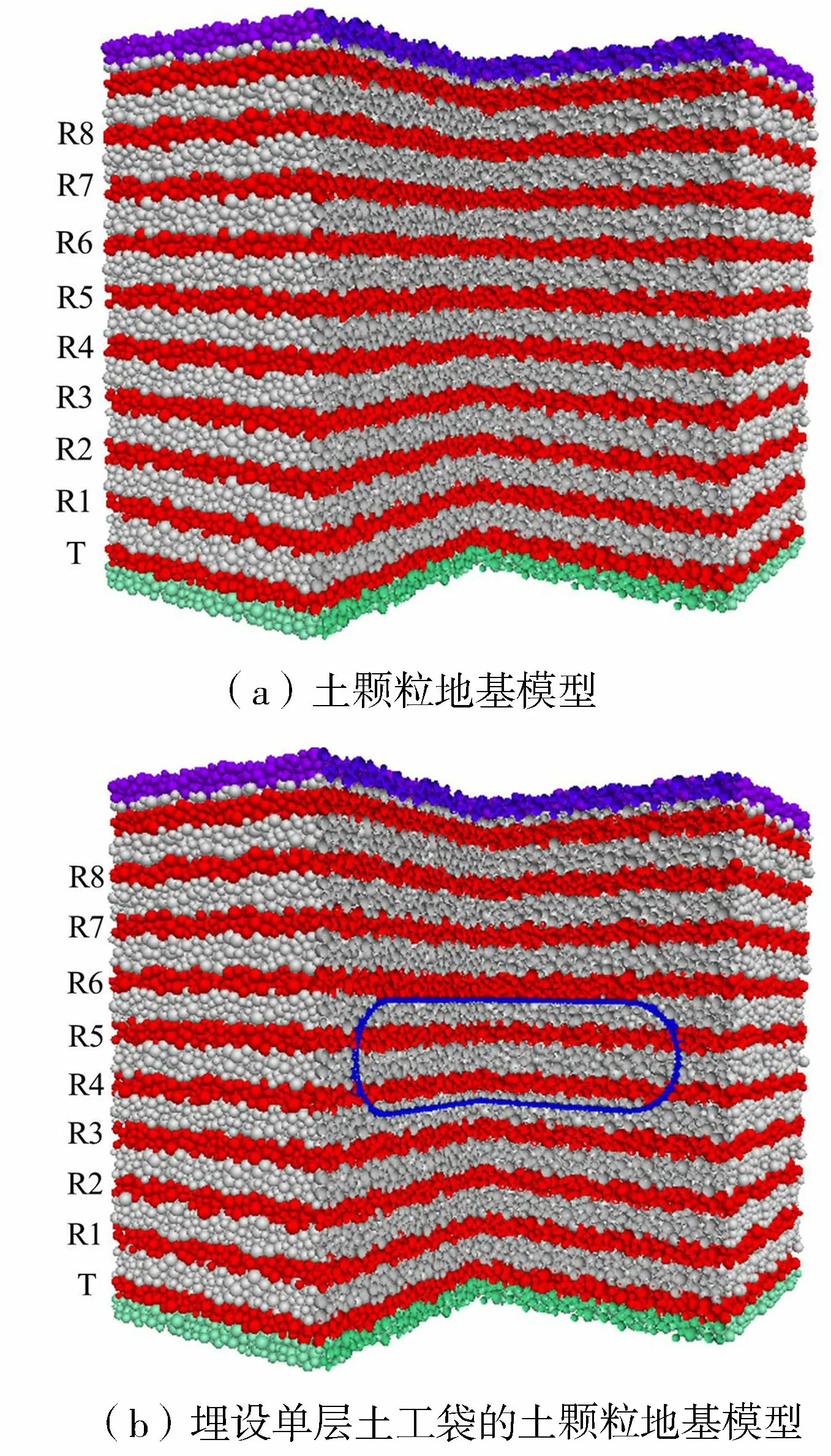
图2 DEM模型Fig.2 DEM model of foundation containing a single-layered soilbag

1.3 输入波

同时移动地基底部第一层的所有颗粒(图2中的绿色部分)可以产生弹性波，颗粒移动方向为竖向时产生P波(压缩波)，颗粒移动方向为水平方向则产生S波(剪切波)。输入波形为频率500 Hz的正弦函数。输入正弦波的幅值取颗粒间平均重叠量的1/100，以确保产生波为弹性波(即颗粒之间没有相对滑动产生)。

2 弹性波波速与衰减计算

2.1 时域中波速的计算

在每两个代表体积之间，将两倍平均粒径厚度的薄层(图2中的红色部分)作为测量域，以记录薄层中颗粒的平均速度。最底部薄层作为发射器(T)，从下往上第2个至倒数第2个薄层作为接收器(R1～R8)。根据发射器和接收器之间的距离L和传播时间Δt计算波速

v=L/Δt

(3)

如图3(a)所示，波的传播时间取决于发射器和接收器弹性波波形特征点之间的距离[18]。在输入波频率为500 Hz、围压为100 kPa时，波峰位置与传播时间之间的关系几乎呈线性，可以用直线进行拟合，如图3(b)所示。

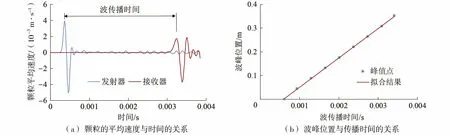
图3 采用峰值-峰值方法确定传播时间Fig.3 Determination of propagation time by the peak-to-peak method

2.2 频域中品质因子计算

弹性波在岩土材料中的衰减通常可以用无量纲的品质因子Q来表征[19]，其定义为谐振器中存储在振荡周期内的峰值能量与该周期内每弧度损失的能量之比：

(4)

品质因子与阻尼比λ直接相关，其关系为

λ=1/(2Q)

(5)

式中λ为动态荷载作用下一个循环中的能量损失量[20]。Tonn[21]研究了品质因子Q的多种计算方法，发现在噪声较小的情况下，频谱比方法计算效果较好。本文采用频谱比法，假设在波传播过程中，两个离散时间的傅里叶幅值之比随频率的变化而变化，两种不同距离上的频谱比计算公式为

(6)

假设右侧关于频率f的斜率为m，可得

(7)

然后便可以计算得到Q：

(8)

图4为平均粒子速度与发射和接收切片频率的傅里叶频谱。在波传播过程中，高频分量的衰减比低频分量的衰减快，因此小波频率降低，脉冲变宽(图3时域结果可见)。

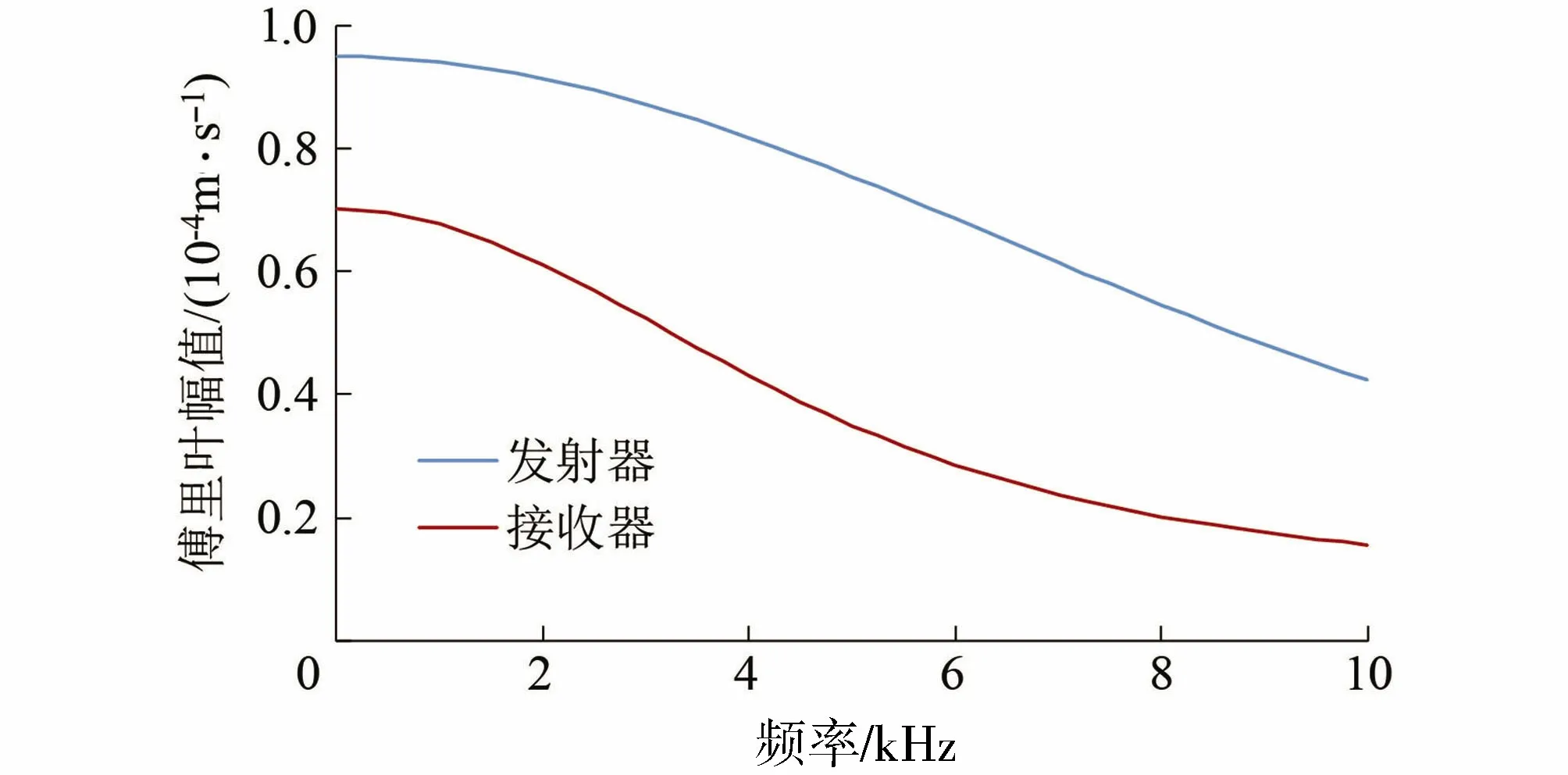
图4 发射器与接收器的傅里叶频谱Fig.4 Fourier spectrum at transmission and receiver

发射器和接收器的傅里叶幅值的对数之比如图5所示。Q可以通过在有限的频率范围内采用直线拟合对数坐标下的傅里叶幅值对数比来估算。

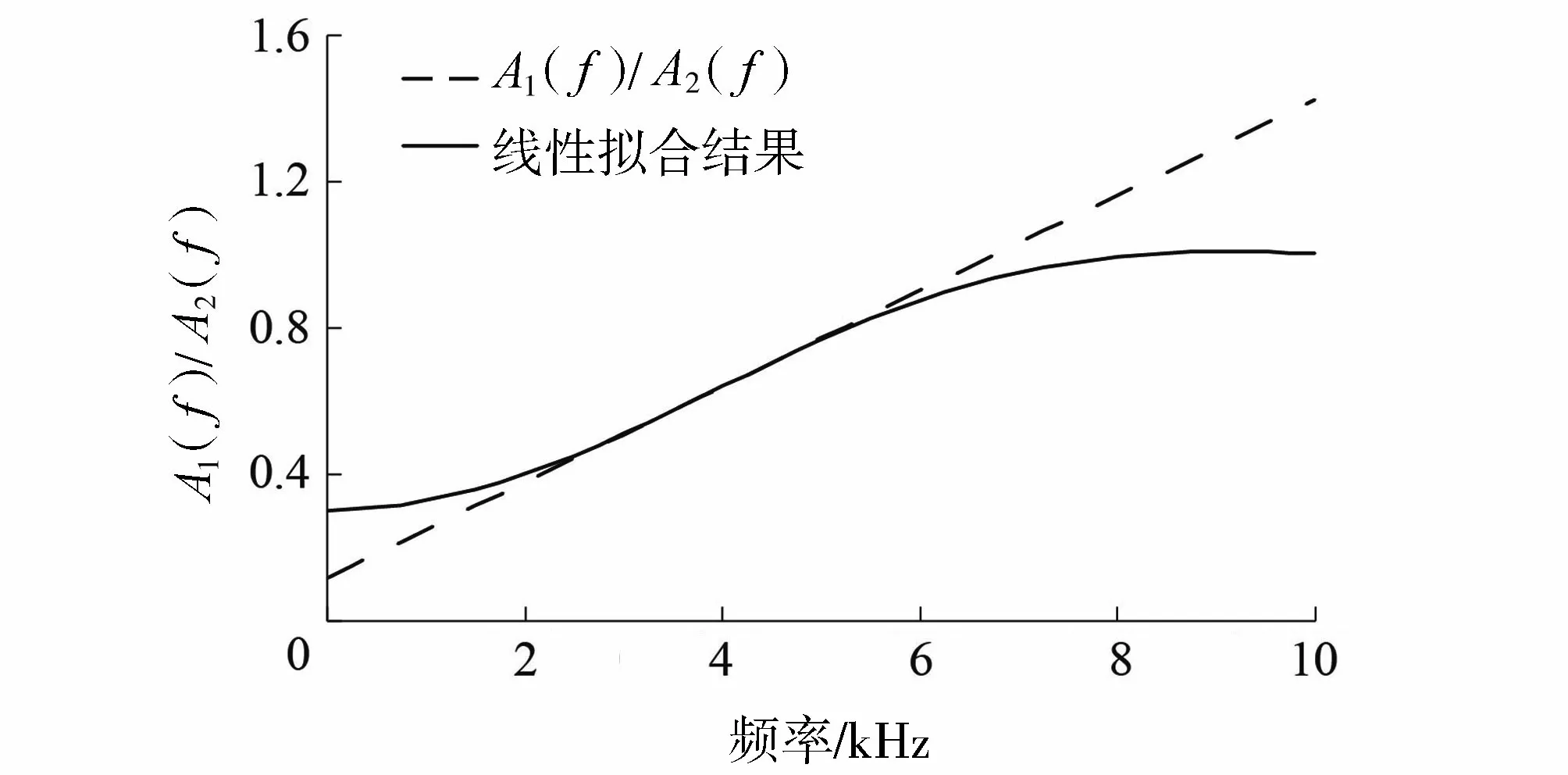
图5 傅里叶幅值对数比的线性拟合Fig.5 Linear fitting of the logarithmic Fourier amplitude spectral ratio

3 结果与讨论

弹性波穿越两种地基的过程中，每个薄层内所有颗粒平均速度随时间的变化可以用波形曲线表示。图6为不同位置处弹性波传播至第一个峰值前的颗粒平均速度波形曲线。由图6可知，在各向同性颗粒材料(土颗粒地基)中，弹性波传播过程土颗粒平均速度变化的波形相似，峰值速度沿传播距离下降均匀，且P波与S波的数值计算结果相近。而在埋设土工袋的地基中，弹性波在穿越土工袋上、下层土工合成材料界面时(图6中红色箭头所示)，其幅值均有一次大幅下降，S波的下降幅度较P波更大，说明土工袋的存在对弹性波产生了削弱作用，且对S波的影响更大。

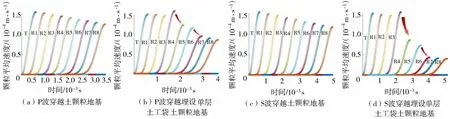
图6 弹性波传播至第一个峰值前的颗粒平均速度波形曲线Fig.6 Waveform curve before the wave propagates to the first peak

弹性波的波速可以根据每个测试区域颗粒平均速度达到峰值的时刻(即弹性波到达每个测试区域的时刻)进行计算。表1为P波与S波在两种地基中的波速情况。由表1可知，在土颗粒地基与埋设土工袋的土颗粒地基中，P波的波速均约为S波波速的1.5倍，与实际情况吻合。弹性波穿越埋设单层土工袋的土颗粒地基时波速略低于穿越土颗粒地基时的波速。图7为两种地基中弹性波传播至不同位置处波速的变化。由图7可知P波与S波穿越土工袋时波速变化规律大体相近，在弹性波进入和离开袋子之前，波速均下降。在土工袋内部与穿越土工袋后，弹性波波速与在土颗粒地基中传播的波速相近，说明在弹性波的传播过程中，仅在穿越土工袋部分时波速有所降低。

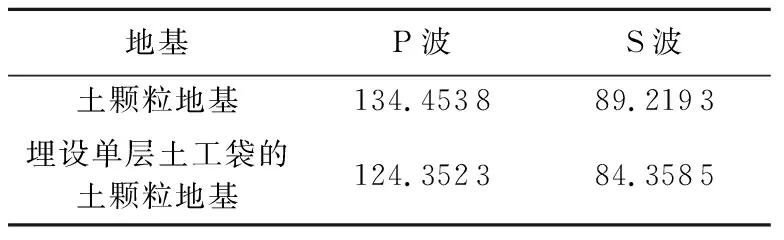
表1 地基中P波与S波的波速 单位：m/s

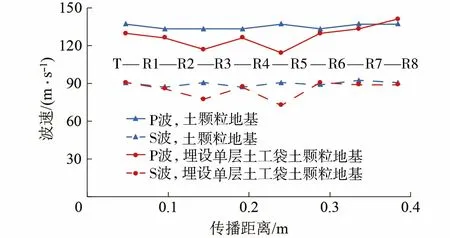
图7 弹性波传播至不同位置处波速的变化Fig.7 Change of wave velocity when elastic wave propagates to different position

表2为P波与S波传播作用下两种地基的Q。由表2可以发现，无论是P波还是S波，在传播过程中，埋设单层土工袋的土颗粒地基的Q均小于土颗粒地基，说明土工袋具有良好的消能效果。图8为弹性波传播至不同位置处Q的变化。由图8可知，在土颗粒地基中，Q随传播距离的增大而增大；当弹性波穿越土工袋时，Q在弹性波穿过土工袋上、下层土工合成材料界面之前发生突降，与波速穿越土工袋时的下降规律相近。说明土工袋对弹性波的衰减作用主要集中在穿越上、下层土工合成材料界面。埋设单层土工袋的土颗粒地基中S波传播到最后一个测点时Q发生突变，这是边界效应影响造成的。

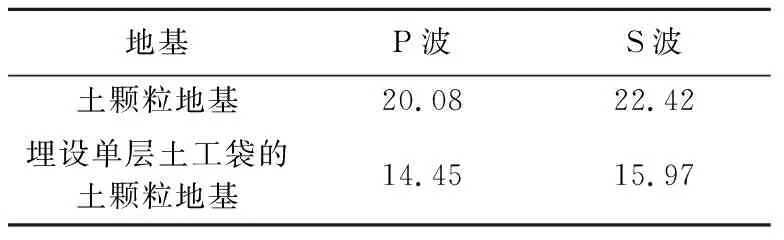
表2 P波与S波传播作用下两种地基的Q

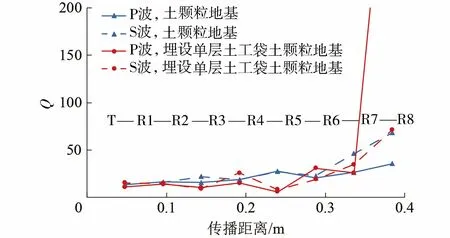
图8 弹性波传播至不同位置处Q的变化Fig.8 Change of Q when elastic wave propagates to different position

4 结 论

a.地基中埋设土工袋，使弹性波的波速略有降低，并增大了地基的阻尼比，说明土工袋具有良好的减振效果。

b.在100 kPa围压、500 Hz弹性波输入条件下，P波与S波穿越土工袋时波速变化规律大体相近，在弹性波进入和离开土工袋时，波速均下降。

c.当弹性波穿越土工袋时，品质因子在弹性波穿过土工袋上、下层土工合成材料界面之前发生突降，说明土工袋对弹性波的衰减作用主要集中在穿越土工袋上、下层土工合成材料界面之前。